2018-2019学年人教A版高中数学必修二检测:第三单元 单元质量测评.DOC
文档属性
| 名称 | 2018-2019学年人教A版高中数学必修二检测:第三单元 单元质量测评.DOC |  | |
| 格式 | zip | ||
| 文件大小 | 64.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-18 17:27:43 | ||
图片预览



文档简介
第三章 单元质量测评
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.
第Ⅰ卷 (选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.直线x+y+1=0的倾斜角为( )
A.30° B.60° C.120° D.150°
答案 D
解析 根据一般式方程,其斜率k=-=-,从而tanα=-,故直线的倾斜角为150°.
2.若直线l与直线y=1,x=7分别交于P,Q,且线段PQ的中点坐标为(1,-1),则直线l的斜率为( )
A. B.- C.3 D.-3
答案 B
解析 设P(a,1),Q(7,b),则有
∴故直线l的斜率为=-.
3.已知直线x-2y+m=0(m>0)与直线x+ny-3=0互相平行,且它们间的距离是,则m+n=( )
A.0 B.1 C.-1 D.2
答案 A
解析 由题意,所给两条直线平行,∴n=-2.由两条平行直线间的距离公式,得d===,解得m=2或m=-8(舍去),∴m+n=0.
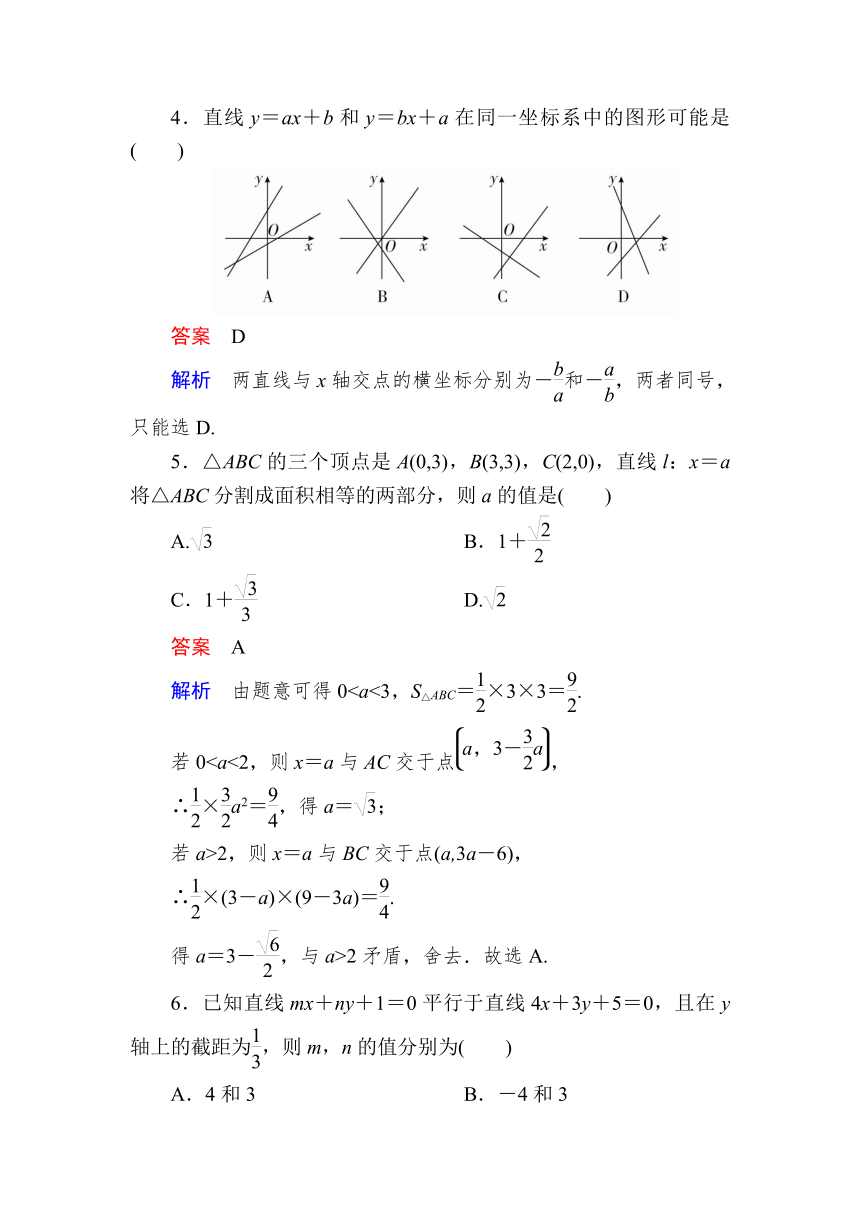
4.直线y=ax+b和y=bx+a在同一坐标系中的图形可能是( )
答案 D
解析 两直线与x轴交点的横坐标分别为-和-,两者同号,只能选D.
5.△ABC的三个顶点是A(0,3),B(3,3),C(2,0),直线l:x=a将△ABC分割成面积相等的两部分,则a的值是( )
A. B.1+
C.1+ D.
答案 A
解析 由题意可得0若0∴×a2=,得a=;
若a>2,则x=a与BC交于点(a,3a-6),
∴×(3-a)×(9-3a)=.
得a=3-,与a>2矛盾,舍去.故选A.
6.已知直线mx+ny+1=0平行于直线4x+3y+5=0,且在y轴上的截距为,则m,n的值分别为( )
A.4和3 B.-4和3
C.-4和-3 D.4和-3
答案 C
解析 由已知可知解得
7.已知点P(0,-1),点Q在直线x-y+1=0上,若直线PQ垂直于直线x+2y-5=0,则点Q的坐标是( )
A.(-2,1) B.(2,1)
C.(2,3) D.(-2,-1)
答案 C
解析 由题意,设点Q(x,x+1),因直线PQ垂直于直线x+2y-5=0,则·=-1,解得x=2.
8.如果AB<0,BC<0,那么直线Ax+By+C=0不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案 D
解析 Ax+By+C=0可化为y=-x-,由AB<0,BC<0,得->0,->0,故直线Ax+By+C=0经过第一、二、三象限,不经过第四象限.
9.将一张画有平面直角坐标系的图纸折叠一次,使得点A(0,2)与点B(4,0)重合,若此时点C(7,3)与点D(m,n)也重合,则m+n的值为( )
A. B. C. D.
答案 A
解析 根据题意,得到折痕为A,B的对称轴,也是C,D的对称轴;kAB==-,且AB的中点坐标为(2,1),所以图纸的折痕所在的直线方程为y-1=2(x-2).
∴kCD==-,①
CD的中点坐标为,
所以-1=2,②
由①②解得m=,n=,∴m+n=.故选A.
10.已知点A(-3,8)和B(2,2),在x轴上求一点M,使|AM|+|BM|最小,那么点M的坐标为( )
A.(-1,0) B.(1,0)
C.(4.4,0) D.(0,4.4)
答案 B
解析 点B关于x轴的对称点为B′(2,-2),
∴AB′方程为=,即2x+y-2=0,
当y=0时,x=1,∴点M的坐标为(1,0).
11.等腰直角三角形ABC中,∠C=90°,若点A,C的坐标分别为(0,4),(3,3),则点B的坐标可能是( )
A.(2,0)或(4,6) B.(2,0)或(6,4)
C.(4,6) D.(0,2)
答案 A
解析 设B(x,y),根据题意可得
即
解得或所以B(2,0)或B(4,6).
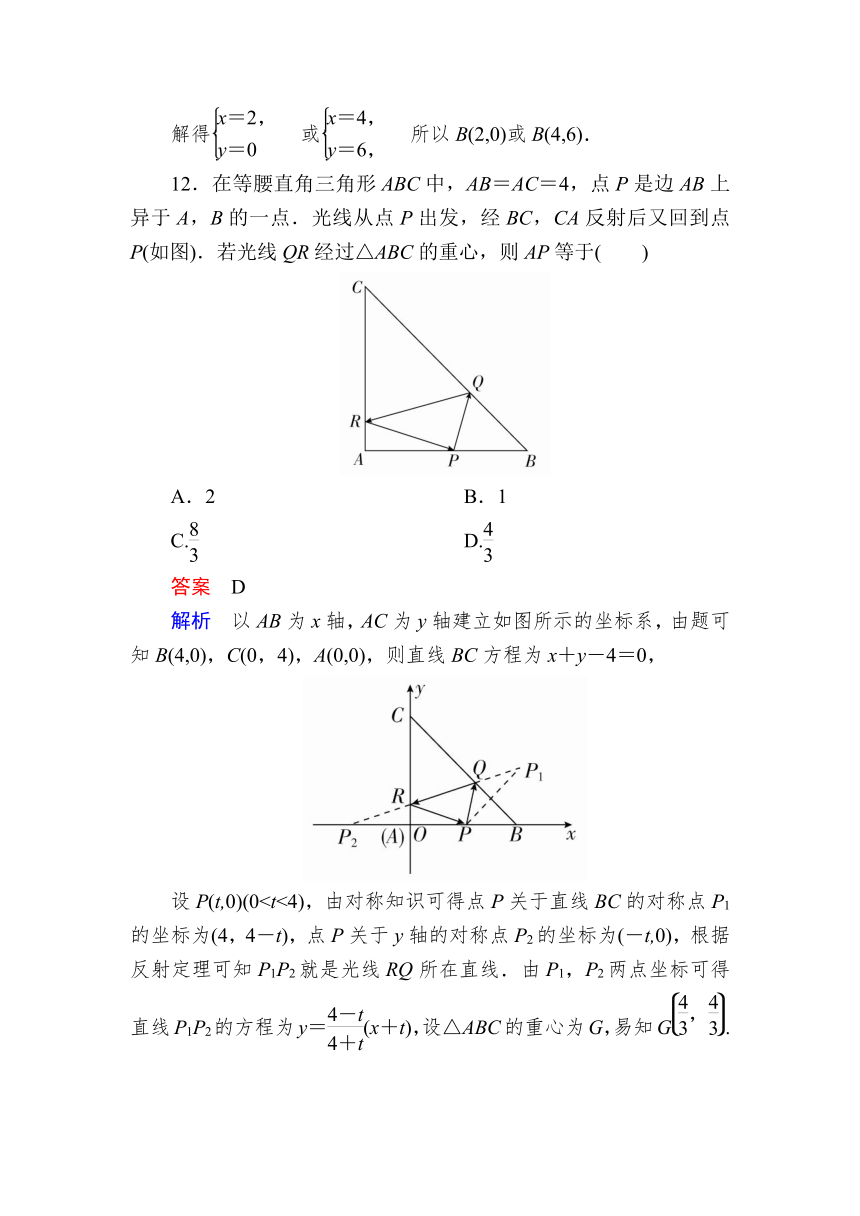
12.在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )
A.2 B.1
C. D.
答案 D
解析 以AB为x轴,AC为y轴建立如图所示的坐标系,由题可知B(4,0),C(0,4),A(0,0),则直线BC方程为x+y-4=0,
设P(t,0)(0所以t=0或t=,因为0第Ⅱ卷 (非选择题,共90分)
二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)
13.若过点P(1-a,1+a)与点Q(3,2a)的直线的倾斜角是钝角,则实数a的取值范围是________.
答案 (-2,1)
解析 设直线的斜率k==<0,得-214.已知直线l的斜率为,且和坐标轴围成的三角形的面积为3,则直线l的方程为________.
答案 x-6y+6=0或x-6y-6=0
解析 设直线l的方程为+=1,
∴|ab|=3,且-=,解得a=-6,b=1或a=6,b=-1,∴直线l的方程为+y=1或-y=1,即x-6y+6=0或x-6y-6=0.
15.两条平行线分别过点P(-2,-2),Q(1,3),它们之间的距离为d,如果这两条直线各自绕点P,Q旋转并互相保持平行,则d的范围是________.
答案 0解析 由下图可知,当这两条直线l1,l2与直线PQ垂直时,d达到最大值,此时
d=|PQ|
==,
∴016.设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于点P(x,y),则|PA|·|PB|的最大值是________.
答案 5
解析 易知A(0,0),B(1,3),且PA⊥PB,
∴|PA|2+|PB|2=|AB|2=10,
∴|PA|·|PB|≤=5(当且仅当|PA|=|PB|时取“=”).
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)直线l1过点A(0,1),l2过点B(5,0),如果l1∥l2,且l1与l2的距离为5,求直线l1与l2的方程.
解 当l1,l2的斜率不存在,即l1:x=0,l2:x=5时,满足条件.
当l1,l2的斜率存在时,设l1:y=kx+1,即kx-y+1=0,
l2:y=k(x-5),即kx-y-5k=0,由两条平行直线间的距离公式得=5,解得k=.
此时l1:12x-5y+5=0,l2:12x-5y-60=0.
综上所述,所求直线l1,l2的方程为l1:x=0,l2:x=5或l1:12x-5y+5=0,l2:12x-5y-60=0.
18.(本小题满分12分)已知两条直线l1:x+m2y+6=0,l2:(m-2)x+3my+2m=0,当m为何值时,l1与l2
(1)相交;
(2)平行;
(3)重合.
解 当m=0时,l1:x+6=0,l2:x=0,∴l1∥l2.
当m=2时,l1:x+4y+6=0,l2:3y+2=0,
∴l1与l2相交.
当m≠0且m≠2时,由=得m=-1或m=3,
由=,得m=3.
故(1)当m≠-1且m≠3且m≠0时,l1与l2相交.
(2)当m=-1或m=0时,l1∥l2.
(3)当m=3时,l1与l2重合.
19.(本小题满分12分)已知点A(m-1,2),B(1,1),C(3,m2-m-1).
(1)若A,B,C三点共线,求实数m的值;
(2)若AB⊥BC,求实数m的值.
解 (1)因为A,B,C三点共线,且xB≠xC,则该直线斜率存在,则kBC=kAB,即=,解得m=1或1-或1+.
(2)由已知,得kBC=,且xA-xB=m-2.
①当m-2=0,即m=2时,直线AB的斜率不存在,此时kBC=0,于是AB⊥BC;
②当m-2≠0,即m≠2时,kAB=,由kAB·kBC=-1,得·=-1,解得m=-3.
综上,可得实数m的值为2或-3.
20.(本小题满分12分)已知点P(2,-1),求:
(1)过点P且与原点的距离为2的直线方程;
(2)过点P且与原点的距离最大的直线方程,并求出最大值;
(3)是否存在过点P且与原点的距离为6的直线?若存在,求出该直线的方程;若不存在,请说明理由.
解 (1)当斜率不存在时,方程x=2符合题意;
当直线的斜率存在时,设为k,
则直线方程应为y+1=k(x-2),
即kx-y-2k-1=0.
由题意得=2,
解得k=,
∴直线方程为3x-4y-10=0.
∴符合题意的直线方程为
x-2=0或3x-4y-10=0.
(2)过点P且与原点的距离最大的直线应为过点P且与OP垂直的直线,易求其方程为2x-y-5=0且最大距离d=.
(3)不存在.由于原点到过点P(2,-1)的直线的最大距离为,而6>,故不存在这样的直线.
21.(本小题满分12分)已知直线l1:y=-k(x-a)和直线l2在x轴上的截距相等,且它们的倾斜角互补,又知直线l1过点P(-3,3).如果点Q(2,2)到直线l2的距离为1,求l2的方程.
解 由题意,可设直线l2的方程为y=k(x-a),即kx-y-ak=0,
∵点Q(2,2)到直线l2的距离为1,
∴=1,①
又∵直线l1的方程为y=-k(x-a),且直线l1过点P(-3,3),∴ak=3-3k.②
由①②得=1,两边平方整理得12k2-25k+12=0,解得k=或k=.
∴当k=时,代入②得a=-,此时直线l2的方程4x-3y+3=0;
当k=时,代入②得a=1,此时直线l2的方程为3x-4y-3=0.
综上所述,直线l2的方程为4x-3y+3=0或3x-4y-3=0.
22.(本小题满分12分)已知三条直线l1:mx-y+m=0,l2:x+my-m(m+1)=0,l3:(m+1)x-y+(m+1)=0,它们围成△ABC.
(1)求证:不论m取何值时,△ABC中总有一个顶点为定点;
(2)当m取何值时,△ABC的面积取最值?并求出最值.
解 (1)证明:设直线l1与直线l3的交点为A.
由
解得
∴点A的坐标为(-1,0),
∴不论m取何值,△ABC中总有一个顶点A(-1,0)为定点.
(2)由
解得
即l2与l3交点为B(0,m+1).
再由
解得
即l1与l2交点为C.
设边AB上的高为h,又直线AB的方程为+=1,即(m+1)x-y+m+1=0,
∴S△ABC=|AB|·h=··
=·=·
=.
当m=0时,S=;当m≠0时,S=1+.
∵函数f(x)=x+的值域为(-∞,-2]∪[2,+∞).
∴-≤<0或0<≤,
∴≤S<或当m=1时,△ABC的面积取最大值为;
当m=-1时,△ABC的面积取最小值为.
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.
第Ⅰ卷 (选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.直线x+y+1=0的倾斜角为( )
A.30° B.60° C.120° D.150°
答案 D
解析 根据一般式方程,其斜率k=-=-,从而tanα=-,故直线的倾斜角为150°.
2.若直线l与直线y=1,x=7分别交于P,Q,且线段PQ的中点坐标为(1,-1),则直线l的斜率为( )
A. B.- C.3 D.-3
答案 B
解析 设P(a,1),Q(7,b),则有
∴故直线l的斜率为=-.
3.已知直线x-2y+m=0(m>0)与直线x+ny-3=0互相平行,且它们间的距离是,则m+n=( )
A.0 B.1 C.-1 D.2
答案 A
解析 由题意,所给两条直线平行,∴n=-2.由两条平行直线间的距离公式,得d===,解得m=2或m=-8(舍去),∴m+n=0.
4.直线y=ax+b和y=bx+a在同一坐标系中的图形可能是( )
答案 D
解析 两直线与x轴交点的横坐标分别为-和-,两者同号,只能选D.
5.△ABC的三个顶点是A(0,3),B(3,3),C(2,0),直线l:x=a将△ABC分割成面积相等的两部分,则a的值是( )
A. B.1+
C.1+ D.
答案 A
解析 由题意可得0
若a>2,则x=a与BC交于点(a,3a-6),
∴×(3-a)×(9-3a)=.
得a=3-,与a>2矛盾,舍去.故选A.
6.已知直线mx+ny+1=0平行于直线4x+3y+5=0,且在y轴上的截距为,则m,n的值分别为( )
A.4和3 B.-4和3
C.-4和-3 D.4和-3
答案 C
解析 由已知可知解得
7.已知点P(0,-1),点Q在直线x-y+1=0上,若直线PQ垂直于直线x+2y-5=0,则点Q的坐标是( )
A.(-2,1) B.(2,1)
C.(2,3) D.(-2,-1)
答案 C
解析 由题意,设点Q(x,x+1),因直线PQ垂直于直线x+2y-5=0,则·=-1,解得x=2.
8.如果AB<0,BC<0,那么直线Ax+By+C=0不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案 D
解析 Ax+By+C=0可化为y=-x-,由AB<0,BC<0,得->0,->0,故直线Ax+By+C=0经过第一、二、三象限,不经过第四象限.
9.将一张画有平面直角坐标系的图纸折叠一次,使得点A(0,2)与点B(4,0)重合,若此时点C(7,3)与点D(m,n)也重合,则m+n的值为( )
A. B. C. D.
答案 A
解析 根据题意,得到折痕为A,B的对称轴,也是C,D的对称轴;kAB==-,且AB的中点坐标为(2,1),所以图纸的折痕所在的直线方程为y-1=2(x-2).
∴kCD==-,①
CD的中点坐标为,
所以-1=2,②
由①②解得m=,n=,∴m+n=.故选A.
10.已知点A(-3,8)和B(2,2),在x轴上求一点M,使|AM|+|BM|最小,那么点M的坐标为( )
A.(-1,0) B.(1,0)
C.(4.4,0) D.(0,4.4)
答案 B
解析 点B关于x轴的对称点为B′(2,-2),
∴AB′方程为=,即2x+y-2=0,
当y=0时,x=1,∴点M的坐标为(1,0).
11.等腰直角三角形ABC中,∠C=90°,若点A,C的坐标分别为(0,4),(3,3),则点B的坐标可能是( )
A.(2,0)或(4,6) B.(2,0)或(6,4)
C.(4,6) D.(0,2)
答案 A
解析 设B(x,y),根据题意可得
即
解得或所以B(2,0)或B(4,6).
12.在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )
A.2 B.1
C. D.
答案 D
解析 以AB为x轴,AC为y轴建立如图所示的坐标系,由题可知B(4,0),C(0,4),A(0,0),则直线BC方程为x+y-4=0,
设P(t,0)(0
二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)
13.若过点P(1-a,1+a)与点Q(3,2a)的直线的倾斜角是钝角,则实数a的取值范围是________.
答案 (-2,1)
解析 设直线的斜率k==<0,得-2
答案 x-6y+6=0或x-6y-6=0
解析 设直线l的方程为+=1,
∴|ab|=3,且-=,解得a=-6,b=1或a=6,b=-1,∴直线l的方程为+y=1或-y=1,即x-6y+6=0或x-6y-6=0.
15.两条平行线分别过点P(-2,-2),Q(1,3),它们之间的距离为d,如果这两条直线各自绕点P,Q旋转并互相保持平行,则d的范围是________.
答案 0
d=|PQ|
==,
∴0
答案 5
解析 易知A(0,0),B(1,3),且PA⊥PB,
∴|PA|2+|PB|2=|AB|2=10,
∴|PA|·|PB|≤=5(当且仅当|PA|=|PB|时取“=”).
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)直线l1过点A(0,1),l2过点B(5,0),如果l1∥l2,且l1与l2的距离为5,求直线l1与l2的方程.
解 当l1,l2的斜率不存在,即l1:x=0,l2:x=5时,满足条件.
当l1,l2的斜率存在时,设l1:y=kx+1,即kx-y+1=0,
l2:y=k(x-5),即kx-y-5k=0,由两条平行直线间的距离公式得=5,解得k=.
此时l1:12x-5y+5=0,l2:12x-5y-60=0.
综上所述,所求直线l1,l2的方程为l1:x=0,l2:x=5或l1:12x-5y+5=0,l2:12x-5y-60=0.
18.(本小题满分12分)已知两条直线l1:x+m2y+6=0,l2:(m-2)x+3my+2m=0,当m为何值时,l1与l2
(1)相交;
(2)平行;
(3)重合.
解 当m=0时,l1:x+6=0,l2:x=0,∴l1∥l2.
当m=2时,l1:x+4y+6=0,l2:3y+2=0,
∴l1与l2相交.
当m≠0且m≠2时,由=得m=-1或m=3,
由=,得m=3.
故(1)当m≠-1且m≠3且m≠0时,l1与l2相交.
(2)当m=-1或m=0时,l1∥l2.
(3)当m=3时,l1与l2重合.
19.(本小题满分12分)已知点A(m-1,2),B(1,1),C(3,m2-m-1).
(1)若A,B,C三点共线,求实数m的值;
(2)若AB⊥BC,求实数m的值.
解 (1)因为A,B,C三点共线,且xB≠xC,则该直线斜率存在,则kBC=kAB,即=,解得m=1或1-或1+.
(2)由已知,得kBC=,且xA-xB=m-2.
①当m-2=0,即m=2时,直线AB的斜率不存在,此时kBC=0,于是AB⊥BC;
②当m-2≠0,即m≠2时,kAB=,由kAB·kBC=-1,得·=-1,解得m=-3.
综上,可得实数m的值为2或-3.
20.(本小题满分12分)已知点P(2,-1),求:
(1)过点P且与原点的距离为2的直线方程;
(2)过点P且与原点的距离最大的直线方程,并求出最大值;
(3)是否存在过点P且与原点的距离为6的直线?若存在,求出该直线的方程;若不存在,请说明理由.
解 (1)当斜率不存在时,方程x=2符合题意;
当直线的斜率存在时,设为k,
则直线方程应为y+1=k(x-2),
即kx-y-2k-1=0.
由题意得=2,
解得k=,
∴直线方程为3x-4y-10=0.
∴符合题意的直线方程为
x-2=0或3x-4y-10=0.
(2)过点P且与原点的距离最大的直线应为过点P且与OP垂直的直线,易求其方程为2x-y-5=0且最大距离d=.
(3)不存在.由于原点到过点P(2,-1)的直线的最大距离为,而6>,故不存在这样的直线.
21.(本小题满分12分)已知直线l1:y=-k(x-a)和直线l2在x轴上的截距相等,且它们的倾斜角互补,又知直线l1过点P(-3,3).如果点Q(2,2)到直线l2的距离为1,求l2的方程.
解 由题意,可设直线l2的方程为y=k(x-a),即kx-y-ak=0,
∵点Q(2,2)到直线l2的距离为1,
∴=1,①
又∵直线l1的方程为y=-k(x-a),且直线l1过点P(-3,3),∴ak=3-3k.②
由①②得=1,两边平方整理得12k2-25k+12=0,解得k=或k=.
∴当k=时,代入②得a=-,此时直线l2的方程4x-3y+3=0;
当k=时,代入②得a=1,此时直线l2的方程为3x-4y-3=0.
综上所述,直线l2的方程为4x-3y+3=0或3x-4y-3=0.
22.(本小题满分12分)已知三条直线l1:mx-y+m=0,l2:x+my-m(m+1)=0,l3:(m+1)x-y+(m+1)=0,它们围成△ABC.
(1)求证:不论m取何值时,△ABC中总有一个顶点为定点;
(2)当m取何值时,△ABC的面积取最值?并求出最值.
解 (1)证明:设直线l1与直线l3的交点为A.
由
解得
∴点A的坐标为(-1,0),
∴不论m取何值,△ABC中总有一个顶点A(-1,0)为定点.
(2)由
解得
即l2与l3交点为B(0,m+1).
再由
解得
即l1与l2交点为C.
设边AB上的高为h,又直线AB的方程为+=1,即(m+1)x-y+m+1=0,
∴S△ABC=|AB|·h=··
=·=·
=.
当m=0时,S=;当m≠0时,S=1+.
∵函数f(x)=x+的值域为(-∞,-2]∪[2,+∞).
∴-≤<0或0<≤,
∴≤S<或
当m=-1时,△ABC的面积取最小值为.
