2018-2019学年高中数学选修2-2人教版练习:评估验收卷(二)
文档属性
| 名称 | 2018-2019学年高中数学选修2-2人教版练习:评估验收卷(二) |  | |
| 格式 | zip | ||
| 文件大小 | 65.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-18 17:29:12 | ||
图片预览




文档简介
评估验收卷(二)
(时间:120分钟 满分:150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求)
1.下列三句话按“三段论”模式排列顺序正确的是( )
①y=cos x(x∈R)是三角函数;
②三角函数是周期函数;
③y=cos x(x∈R)是周期函数.
A.①②③ B.②①③
C.②③① D.③②①
解析:按三段论的模式,排列顺序正确的是②①③.选B.
答案:B
2.用反证法证明命题“已知x,y∈N*,如果xy可被7整除,那么x,y至少有一个能被7整除”时,假设的内容是( )
A.x,y都不能被7整除
B.x,y都能被7整除
C.x,y只有一个能被7整除
D.只有x不能被7整除
解析:用反证法证明命题时,先假设命题的否定成立,再进行推证.“x,y至少有一个能被7整除”的否定是“x,y都不能被7整除”.
答案:A
3.用数学归纳法证明“5n-2n能被3整除”的第二步中,当n=k+1时,为了使用假设,应将5k+1-2k+1变形为( )
A.(5k-2k)+4×5k-2k
B.5(5k-2k)+3×2k
C.(5-2)(5k-2k)
D.2(5k-2k)-3×5k
解析:5k+1-2k+1=5k·5-2k·2=5k·5-2k·5+2k·5-2k·2=5(5k-2k)+3·2k.
答案:B
4.已知n为正偶数,用数学归纳法证明1-+-+…-=2时,若已假设n=k(k≥2且k为偶数)时等式成立,则还需要用归纳假设再证n=________时等式成立.( )
A.k+1 B.k+2
C.2k+2 D.2(k+2)
解析:根据数学归纳法的步骤可知,n=k(k≥2且k为偶数)的下一个偶数为n=k+2,故选B.
答案:B
5.已知{bn}为等比数列,b5=2,则b1b2b3…b9=29.若{an}为等差数列,a5=2,则{an}的类似结论为( )
A.a1a2a3…a9=29 B.a1+a2+…+a9=29
C.a1a2a3…a9=2×9 D.a1+a2+…+a9=2×9
解析:由等差数列性质,有a1+a9=a2+a8=…=2a5.易知选项D正确.
答案:D
6.下面是一段“三段论”推理过程:若函数f(x)在(a,b)内可导且单调递增,则在(a,b)内,f′(x)>0恒成立.因为f(x)=x3在(-1,1)内可导且单调递增,所以在(-1,1)内,f′(x)=3x2>0恒成立.以上推理中( )
A.大前提错误 B.小前提错误
C.结论正确 D.推理形式错误
解析:f(x)在(a,b)内可导且单调递增,则在(a,b)内,f′(x)≥0恒成立,故大前提错误,故选A.
答案:A
7.分析法又称执果索因法,若用分析法证明:“设a>b>c,且a+b+c=0,求证A.a-b>0 B.a-c<0
C.(a-b)(a-c)>0 D.(a-b)(a-c)<0
解析:要证明0,即证(a-c)·(2a+c)>0,即证(a-c)(a-b)>0.
答案:C
8.下列各图中线段的条数用an表示,如a1=1,a2=5,若如此作下去,则第8个图中的线段条数a8=( )
A.508 B.509 C.511 D.512
解析:由题图知,a1=1,a2=1+22,a3=1+22+23,a4=1+22+23+24,…,所以a8=1+22+23+…+28=(2+22+23+…+28)-1=-1=509.
答案:B
9.观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10+b10=( )
A.28 B.76 C.123 D.199
解析:记an+bn=f(n),则f(3)=f(1)+f(2)=1+3=4;f(4)=f(2)+f(3)=3+4=7;f(5)=f(3)+f(4)=11.通过观察不难发现f(n)=f(n-1)+f(n-2)(n∈N*,n≥3),则f(6)=f(4)+f(5)=18;f(7)=f(5)+f(6)=29;f(8)=f(6)+f(7)=47;f(9)=f(7)+f(8)=76;f(10)=f(8)+f(9)=123.所以a10+b10=123.
答案:C
10.观察数表:
1
2
3
4
2
3
4
5
3
4
5
6
4
5
6
7
根据数表中反映的规律,第n行与第n列的交叉点上的数应该是( )
A.2n-1 B.2n+1
C.n2-1 D.n2
解析:根据题中数表可知,第1行第1列交叉点上的数为1,第2行第2列交叉点上的数为3,第3行第3列交叉点上的数为5,第4行第4列交叉点上的数为7,那么,由此可以推导出第n行第n列交叉点上的数应该是2n-1.
答案:A
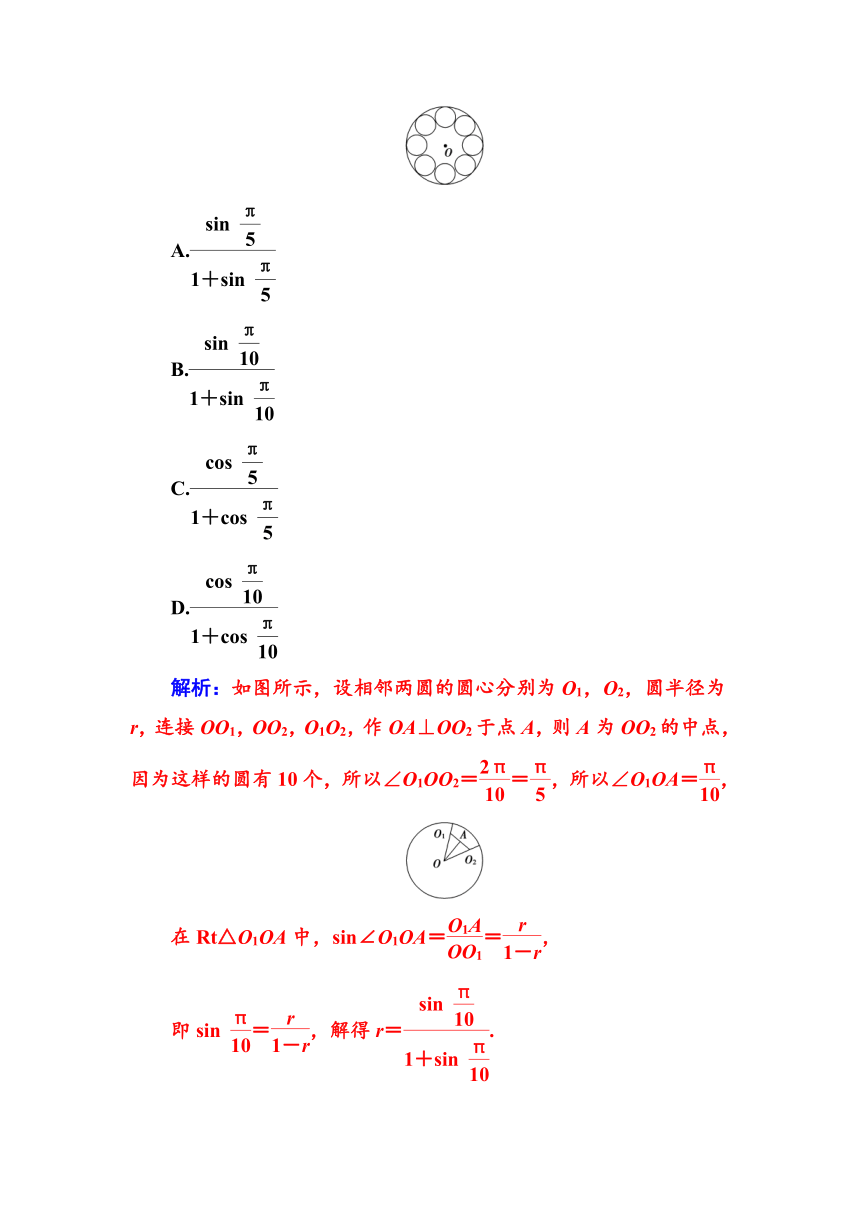
11.如图所示,半径为1的圆O内有n个半径相等的圆依次相切且都与圆O相切,若n=10,则这些等圆的半径为( )
A.
B.
C.
D.
解析:如图所示,设相邻两圆的圆心分别为O1,O2,圆半径为r,连接OO1,OO2,O1O2,作OA⊥OO2于点A,则A为OO2的中点,因为这样的圆有10个,所以∠O1OO2==,所以∠O1OA=,
在Rt△O1OA中,sin∠O1OA==,
即sin =,解得r=.
答案:B
12.请阅读下列材料:若两个正实数a1,a2满足a+a=1,求证:a1+a2≤.证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以Δ≤0,即4(a1+a2)2-8≤0,所以a1+a2≤.
根据上述证明方法,若n个正实数a1,a2,…,an满足a+a+…+a=n时,你能得到的结论是( )
A.a1+a2+…+an≤2n
B. a1+a2+…+an≤n2
C.a1+a2+…+an≤n
D.a1+a2+…+an≤
解析:构造函数f(x)=(x-a1)2+(x-a2)2+…+(x-an)2=nx2-2(a1+a2+…+an)x+n,
因为对一切实数x,恒有f(x)≥0,所以Δ≤0,即4(a1+a2+…+an)2-4n2≤0,所以a1+a2+…+an≤n.
答案:C
二、选择题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.“因为AC,BD是菱形ABCD的对角线,所以AC,BD互相垂直且平分.”补充以上推理的大前提是____________________.
解析:大前提是“菱形的对角线互相垂直且平分”.
答案:菱形的对角线互相垂直且平分
14.我们知道,圆的面积的导数为圆的周长,即:若圆的半径为r,则圆的面积S(r)=πr2,S′(r)=2πr为圆的周长.通过类比,有以下结论:
①正方形面积的导数为正方形的周长;
②正方体体积的导数为正方体的表面积;
③球体的体积的导数为球体的表面积.
其中正确的是________(填序号).
解析:设正方形的边长为a,
则正方形的面积为S(a)=a2,
而S′(a)=2a≠正方形的周长;
设正方体的棱长为a,
则正方体的体积为V(a)=a3,
而V′(a)=3a2≠正方体的表面积;
设球体的半径为r,则V(r)=πr3,
而V′(r)=4πr2=球体的表面积.
所以只有③正确.
答案:③
15.下列给出一个“三角形数阵”,已知每一列数成等差数列,从第三行起,每一行数成等比数列,而且每一行的公比都相等,记第i行第j列的数为aij(i≥j,i,j∈N*),则a53等于________,amn=________(m≥3).
,
,,
,,,
…
解析:由题意可知,第一列首项为,公差d=-=;第二列的首项为,公差d=-=,所以a51=+4×=,由题意知,每行的公比都是,所以a53=a51q2=×=.
由题意知am1=+(m-1)×=,amn=×=,m≥3.
答案:
16.有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
解析:丙的卡片上的数字之和不是5,则丙有两种情况:①丙的卡片上的数字为1和2,此时乙的卡片上的数字为2和3,甲的卡片上的数字为1和3,满足题意;②丙的卡片上的数字为1和3,此时乙的卡片上的数字为2和3,甲的卡片上的数字为1和2,这时甲与乙的卡片上有相同的数字2,与已知矛盾,故情况②不符合,所以甲的卡片上的数字为1和3.
答案:1和3
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)用综合法或分析法证明:
(1)如果a,b>0,则lg≥;
(2)+>2+2.
证明:(1)当a,b>0时,有≥,
所以lg≥lg,
所以lg≥lgab=.
(2)要证+>2+2,
只要证(+)2>(2+2)2,
即2>2,这是显然成立的,
所以,原不等式成立.
18.(本小题满分12分)已知A+B=,且A,B≠kπ+(k∈Z).求证:(1+tan A)(1+tan B)=4.
证明:由A+B=得tan (A+B)=tan ,
即=,
所以tan A+tan B=-tan Atan B.
所以(1+tan A)(1+tan B)=1+(tan A+tan B)+
3tan Atan B=1+(-tan Atan A)+3tan Atan B=4.
故原等式成立.
19.(本小题满分12分)已知△ABC的三边长都是有理数,求证:
(1)cos A是有理数;
(2)对任意正整数n,cos nA和sin A·sin nA是有理数.
证明:(1)由AB、BC、AC为有理数及余弦定理知
cos A=是有理数.
(2)用数学归纳法证明cos nA和sin A·sin nA都是有理数.
①当n=1时,由(1)知cos nA是有理数,
从而有sin A·sin nA=1-cos2 A也是有理数.
②假设当n=k(k≥1)时,
cos kA和sin A·sin kA都是有理数.
当n=k+1时,
由cos(k+1)A=cos A·cos kA-sin A·sin kA,
sin A·sin(k+1)A
=sin A·(sin A·cos kA+cos A·sin kA)
=(sin A·sin A)·cos kA+(sin A·sin kA)·cos A,
由①和归纳假设,知cos (k+1)A和sin A·sin(k+1)A都是有理数.
即当n=k+1时,结论成立.
综合①、②可知,对任意正整数n,cos nA和sin A·sin nA都是有理数.
20.(本小题满分12分)已知a,b,c都是不为零的实数,求证:a2+b2+c2>(ab+bc+ca).
证明:要证a2+b2+c2>(ab+bc+ca) ,
只需证5(a2+b2+c2)>4(ab+bc+ca),
只需证5a2+5b2+5c2-(4ab+4bc+4ca)>0,
只需证(a2-4ab+4b2)+(b2-4bc+4c2)+(c2-4ca+4a2)>0,只需证(a-2b)2+(b-2c)2+(c-2a)2>0.
因为(a-2b)2≥0,(b-2c)2≥0,(c-2a)2≥0 ,
且这三个不等式中等号不可能同时成立(若同时成立等号,则必有a=b=c=0),
所以(a-2b)2+(b-2c)2+(c-2a)2>0,
所以原不等式成立.
21.(本小题满分12分)十字绣有着悠久的历史,如下图,(1)、(2)、(3)、(4)为十字绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图案包含f(n)个小正方形.
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求+++…+(n≥2)的值.
解:(1)按所给图案的规律画出第五个图如图:
由图可得f(5)=41.
(2)由图可得f(2)-f(1)=4×1;
f(3)-f(2)=8=4×2;
f(4)-f(3)=12=4×3;
f(5)-f(4)=16=4×4;
…
由上式规律,可得f(n+1)-f(n)=4n,所以f(n)-f(n-1)=4(n-1).即
f(n)=f(n-1)+4(n-1)
=f(n-2)+4(n-2)+4(n-1)
=f(1)+4(n-1)+4(n-2)+…+4
=1+4[1+2+…+(n-1)]
=2n2-2n+1.
又f(1)=1,所以f(n)=2n2-2n+1.
(3)当n≥2时,===,
所以原式=+
=1+=-.
22.(本小题满分12分)已知函数f(x)=,记数列{an}的前n项和为Sn,且有a1=f(1).当n≥2时,Sn-=(n2+5n-2).
(1)计算a1,a2,a3,a4;
(2)求出数列{an}的通项公式,并给予证明.
解:(1)a1=2,a2=3,a3=4,a4=5.
(2)由(1)猜想an=n+1,下面用数学归纳法证明:
①当n=1时,由(1)可知猜想成立;
②假设n=k(k∈N*)时猜想成立,即ak=k+1,此时sk=(k2+5k-2)+2-ak,
当n=k+1时,Sk+1-=[(k+1)2+5(k+1)-2],
即Sk+ak+1-(2-ak+1)=[(k+1)2+5(k+1)-2],
即(k2+5k-2)+2-ak+ak+1-(2-ak+1)=[(k+1)2+5(k+1)-2],
结合ak=k+1,化简整理得ak+1=k+2,
所以当n=k+1时猜想成立,
综上所述,对任意n∈N*,an=n+1成立.
(时间:120分钟 满分:150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求)
1.下列三句话按“三段论”模式排列顺序正确的是( )
①y=cos x(x∈R)是三角函数;
②三角函数是周期函数;
③y=cos x(x∈R)是周期函数.
A.①②③ B.②①③
C.②③① D.③②①
解析:按三段论的模式,排列顺序正确的是②①③.选B.
答案:B
2.用反证法证明命题“已知x,y∈N*,如果xy可被7整除,那么x,y至少有一个能被7整除”时,假设的内容是( )
A.x,y都不能被7整除
B.x,y都能被7整除
C.x,y只有一个能被7整除
D.只有x不能被7整除
解析:用反证法证明命题时,先假设命题的否定成立,再进行推证.“x,y至少有一个能被7整除”的否定是“x,y都不能被7整除”.
答案:A
3.用数学归纳法证明“5n-2n能被3整除”的第二步中,当n=k+1时,为了使用假设,应将5k+1-2k+1变形为( )
A.(5k-2k)+4×5k-2k
B.5(5k-2k)+3×2k
C.(5-2)(5k-2k)
D.2(5k-2k)-3×5k
解析:5k+1-2k+1=5k·5-2k·2=5k·5-2k·5+2k·5-2k·2=5(5k-2k)+3·2k.
答案:B
4.已知n为正偶数,用数学归纳法证明1-+-+…-=2时,若已假设n=k(k≥2且k为偶数)时等式成立,则还需要用归纳假设再证n=________时等式成立.( )
A.k+1 B.k+2
C.2k+2 D.2(k+2)
解析:根据数学归纳法的步骤可知,n=k(k≥2且k为偶数)的下一个偶数为n=k+2,故选B.
答案:B
5.已知{bn}为等比数列,b5=2,则b1b2b3…b9=29.若{an}为等差数列,a5=2,则{an}的类似结论为( )
A.a1a2a3…a9=29 B.a1+a2+…+a9=29
C.a1a2a3…a9=2×9 D.a1+a2+…+a9=2×9
解析:由等差数列性质,有a1+a9=a2+a8=…=2a5.易知选项D正确.
答案:D
6.下面是一段“三段论”推理过程:若函数f(x)在(a,b)内可导且单调递增,则在(a,b)内,f′(x)>0恒成立.因为f(x)=x3在(-1,1)内可导且单调递增,所以在(-1,1)内,f′(x)=3x2>0恒成立.以上推理中( )
A.大前提错误 B.小前提错误
C.结论正确 D.推理形式错误
解析:f(x)在(a,b)内可导且单调递增,则在(a,b)内,f′(x)≥0恒成立,故大前提错误,故选A.
答案:A
7.分析法又称执果索因法,若用分析法证明:“设a>b>c,且a+b+c=0,求证
C.(a-b)(a-c)>0 D.(a-b)(a-c)<0
解析:要证明
答案:C
8.下列各图中线段的条数用an表示,如a1=1,a2=5,若如此作下去,则第8个图中的线段条数a8=( )
A.508 B.509 C.511 D.512
解析:由题图知,a1=1,a2=1+22,a3=1+22+23,a4=1+22+23+24,…,所以a8=1+22+23+…+28=(2+22+23+…+28)-1=-1=509.
答案:B
9.观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10+b10=( )
A.28 B.76 C.123 D.199
解析:记an+bn=f(n),则f(3)=f(1)+f(2)=1+3=4;f(4)=f(2)+f(3)=3+4=7;f(5)=f(3)+f(4)=11.通过观察不难发现f(n)=f(n-1)+f(n-2)(n∈N*,n≥3),则f(6)=f(4)+f(5)=18;f(7)=f(5)+f(6)=29;f(8)=f(6)+f(7)=47;f(9)=f(7)+f(8)=76;f(10)=f(8)+f(9)=123.所以a10+b10=123.
答案:C
10.观察数表:
1
2
3
4
2
3
4
5
3
4
5
6
4
5
6
7
根据数表中反映的规律,第n行与第n列的交叉点上的数应该是( )
A.2n-1 B.2n+1
C.n2-1 D.n2
解析:根据题中数表可知,第1行第1列交叉点上的数为1,第2行第2列交叉点上的数为3,第3行第3列交叉点上的数为5,第4行第4列交叉点上的数为7,那么,由此可以推导出第n行第n列交叉点上的数应该是2n-1.
答案:A
11.如图所示,半径为1的圆O内有n个半径相等的圆依次相切且都与圆O相切,若n=10,则这些等圆的半径为( )
A.
B.
C.
D.
解析:如图所示,设相邻两圆的圆心分别为O1,O2,圆半径为r,连接OO1,OO2,O1O2,作OA⊥OO2于点A,则A为OO2的中点,因为这样的圆有10个,所以∠O1OO2==,所以∠O1OA=,
在Rt△O1OA中,sin∠O1OA==,
即sin =,解得r=.
答案:B
12.请阅读下列材料:若两个正实数a1,a2满足a+a=1,求证:a1+a2≤.证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以Δ≤0,即4(a1+a2)2-8≤0,所以a1+a2≤.
根据上述证明方法,若n个正实数a1,a2,…,an满足a+a+…+a=n时,你能得到的结论是( )
A.a1+a2+…+an≤2n
B. a1+a2+…+an≤n2
C.a1+a2+…+an≤n
D.a1+a2+…+an≤
解析:构造函数f(x)=(x-a1)2+(x-a2)2+…+(x-an)2=nx2-2(a1+a2+…+an)x+n,
因为对一切实数x,恒有f(x)≥0,所以Δ≤0,即4(a1+a2+…+an)2-4n2≤0,所以a1+a2+…+an≤n.
答案:C
二、选择题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.“因为AC,BD是菱形ABCD的对角线,所以AC,BD互相垂直且平分.”补充以上推理的大前提是____________________.
解析:大前提是“菱形的对角线互相垂直且平分”.
答案:菱形的对角线互相垂直且平分
14.我们知道,圆的面积的导数为圆的周长,即:若圆的半径为r,则圆的面积S(r)=πr2,S′(r)=2πr为圆的周长.通过类比,有以下结论:
①正方形面积的导数为正方形的周长;
②正方体体积的导数为正方体的表面积;
③球体的体积的导数为球体的表面积.
其中正确的是________(填序号).
解析:设正方形的边长为a,
则正方形的面积为S(a)=a2,
而S′(a)=2a≠正方形的周长;
设正方体的棱长为a,
则正方体的体积为V(a)=a3,
而V′(a)=3a2≠正方体的表面积;
设球体的半径为r,则V(r)=πr3,
而V′(r)=4πr2=球体的表面积.
所以只有③正确.
答案:③
15.下列给出一个“三角形数阵”,已知每一列数成等差数列,从第三行起,每一行数成等比数列,而且每一行的公比都相等,记第i行第j列的数为aij(i≥j,i,j∈N*),则a53等于________,amn=________(m≥3).
,
,,
,,,
…
解析:由题意可知,第一列首项为,公差d=-=;第二列的首项为,公差d=-=,所以a51=+4×=,由题意知,每行的公比都是,所以a53=a51q2=×=.
由题意知am1=+(m-1)×=,amn=×=,m≥3.
答案:
16.有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
解析:丙的卡片上的数字之和不是5,则丙有两种情况:①丙的卡片上的数字为1和2,此时乙的卡片上的数字为2和3,甲的卡片上的数字为1和3,满足题意;②丙的卡片上的数字为1和3,此时乙的卡片上的数字为2和3,甲的卡片上的数字为1和2,这时甲与乙的卡片上有相同的数字2,与已知矛盾,故情况②不符合,所以甲的卡片上的数字为1和3.
答案:1和3
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)用综合法或分析法证明:
(1)如果a,b>0,则lg≥;
(2)+>2+2.
证明:(1)当a,b>0时,有≥,
所以lg≥lg,
所以lg≥lgab=.
(2)要证+>2+2,
只要证(+)2>(2+2)2,
即2>2,这是显然成立的,
所以,原不等式成立.
18.(本小题满分12分)已知A+B=,且A,B≠kπ+(k∈Z).求证:(1+tan A)(1+tan B)=4.
证明:由A+B=得tan (A+B)=tan ,
即=,
所以tan A+tan B=-tan Atan B.
所以(1+tan A)(1+tan B)=1+(tan A+tan B)+
3tan Atan B=1+(-tan Atan A)+3tan Atan B=4.
故原等式成立.
19.(本小题满分12分)已知△ABC的三边长都是有理数,求证:
(1)cos A是有理数;
(2)对任意正整数n,cos nA和sin A·sin nA是有理数.
证明:(1)由AB、BC、AC为有理数及余弦定理知
cos A=是有理数.
(2)用数学归纳法证明cos nA和sin A·sin nA都是有理数.
①当n=1时,由(1)知cos nA是有理数,
从而有sin A·sin nA=1-cos2 A也是有理数.
②假设当n=k(k≥1)时,
cos kA和sin A·sin kA都是有理数.
当n=k+1时,
由cos(k+1)A=cos A·cos kA-sin A·sin kA,
sin A·sin(k+1)A
=sin A·(sin A·cos kA+cos A·sin kA)
=(sin A·sin A)·cos kA+(sin A·sin kA)·cos A,
由①和归纳假设,知cos (k+1)A和sin A·sin(k+1)A都是有理数.
即当n=k+1时,结论成立.
综合①、②可知,对任意正整数n,cos nA和sin A·sin nA都是有理数.
20.(本小题满分12分)已知a,b,c都是不为零的实数,求证:a2+b2+c2>(ab+bc+ca).
证明:要证a2+b2+c2>(ab+bc+ca) ,
只需证5(a2+b2+c2)>4(ab+bc+ca),
只需证5a2+5b2+5c2-(4ab+4bc+4ca)>0,
只需证(a2-4ab+4b2)+(b2-4bc+4c2)+(c2-4ca+4a2)>0,只需证(a-2b)2+(b-2c)2+(c-2a)2>0.
因为(a-2b)2≥0,(b-2c)2≥0,(c-2a)2≥0 ,
且这三个不等式中等号不可能同时成立(若同时成立等号,则必有a=b=c=0),
所以(a-2b)2+(b-2c)2+(c-2a)2>0,
所以原不等式成立.
21.(本小题满分12分)十字绣有着悠久的历史,如下图,(1)、(2)、(3)、(4)为十字绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图案包含f(n)个小正方形.
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求+++…+(n≥2)的值.
解:(1)按所给图案的规律画出第五个图如图:
由图可得f(5)=41.
(2)由图可得f(2)-f(1)=4×1;
f(3)-f(2)=8=4×2;
f(4)-f(3)=12=4×3;
f(5)-f(4)=16=4×4;
…
由上式规律,可得f(n+1)-f(n)=4n,所以f(n)-f(n-1)=4(n-1).即
f(n)=f(n-1)+4(n-1)
=f(n-2)+4(n-2)+4(n-1)
=f(1)+4(n-1)+4(n-2)+…+4
=1+4[1+2+…+(n-1)]
=2n2-2n+1.
又f(1)=1,所以f(n)=2n2-2n+1.
(3)当n≥2时,===,
所以原式=+
=1+=-.
22.(本小题满分12分)已知函数f(x)=,记数列{an}的前n项和为Sn,且有a1=f(1).当n≥2时,Sn-=(n2+5n-2).
(1)计算a1,a2,a3,a4;
(2)求出数列{an}的通项公式,并给予证明.
解:(1)a1=2,a2=3,a3=4,a4=5.
(2)由(1)猜想an=n+1,下面用数学归纳法证明:
①当n=1时,由(1)可知猜想成立;
②假设n=k(k∈N*)时猜想成立,即ak=k+1,此时sk=(k2+5k-2)+2-ak,
当n=k+1时,Sk+1-=[(k+1)2+5(k+1)-2],
即Sk+ak+1-(2-ak+1)=[(k+1)2+5(k+1)-2],
即(k2+5k-2)+2-ak+ak+1-(2-ak+1)=[(k+1)2+5(k+1)-2],
结合ak=k+1,化简整理得ak+1=k+2,
所以当n=k+1时猜想成立,
综上所述,对任意n∈N*,an=n+1成立.
