2018-2019学年人教A版高中数学必修一练习:滚动检测4函数的应用
文档属性
| 名称 | 2018-2019学年人教A版高中数学必修一练习:滚动检测4函数的应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 83.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-19 00:00:00 | ||
图片预览

文档简介
滚动检测(四)
(时间:45分钟 满分:75分)
一、选择题(本大题共6小题,每小题5分,共30分.在每小题给出的四个备选项中,只有一项是符合题目要求的)
1.已知f(x)=3ax+1-2a,设在(-1,1)上存在x0使f(x0)=0,则a的取值范围是( )
A.-1
C.a>或a<-1 D.a<-1
解析:∵f(x)是x的一次函数,
∴f(-1)·f(1)<0?a>或a<-1.
答案:C
2.某城市出租车起步价为10元,最长可租乘3 km(含3 km),以后每1 km为1.6元(不足1 km,按1 km计费),若出租车行驶在不需等待的公路上,则出租车的费用y(元)与行驶的里程x(km)之间的函数图象大致为( )
解析:由题意,当0当3当4…
当n -1答案:C
3.已知函数f(x)=ax-3(a>0,且a≠1),f(x0)=0,若x0∈(0,1),则实数a的取值范围是( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,+∞)
解析:本题以函数零点为载体,考查指数函数、对数函数的图象和性质.由f(x0)=0,得ax0-3=0,
∴x0=loga3.又x0∈(0,1),∴03.故选D.
答案:D
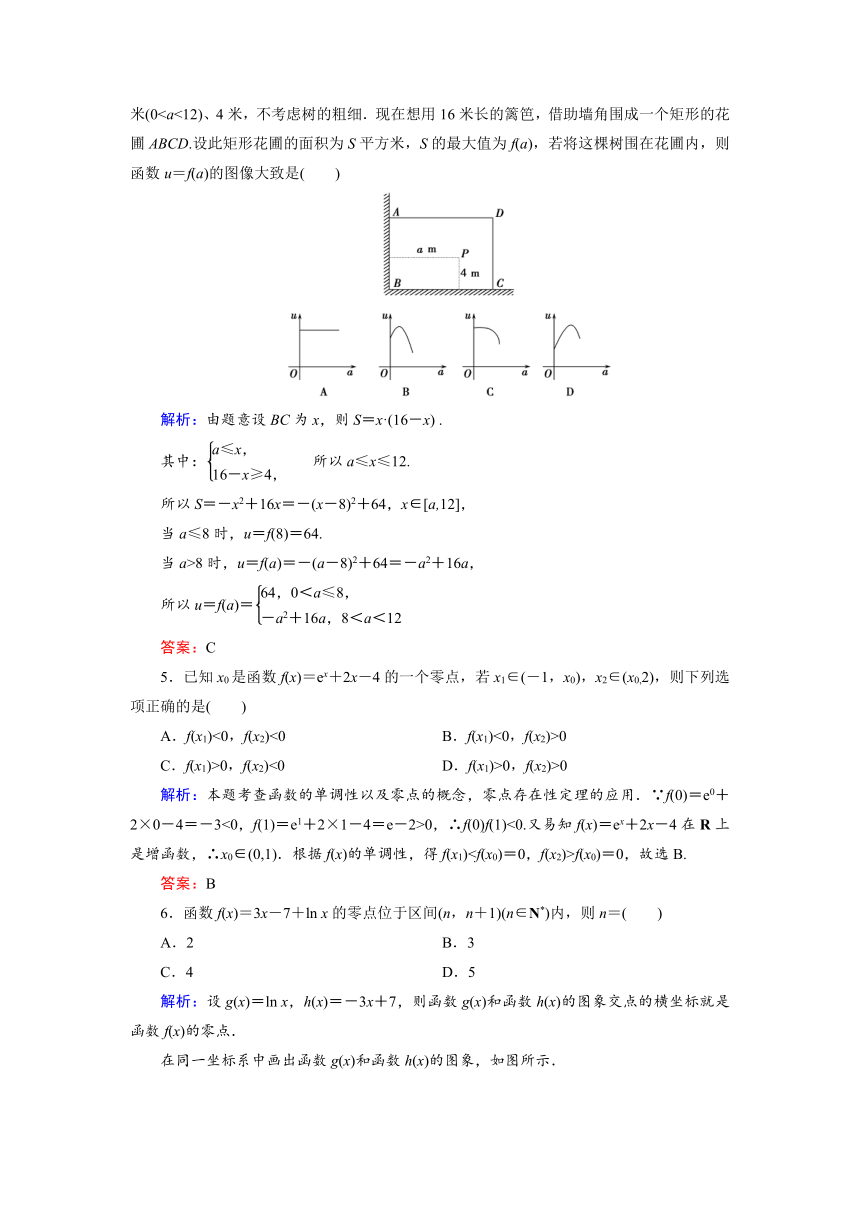
4.如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a米(0
解析:由题意设BC为x,则S=x·(16-x) .
其中: 所以a≤x≤12.
所以S=-x2+16x=-(x-8)2+64,x∈[a,12],
当a≤8时,u=f(8)=64.
当a>8时,u=f(a)=-(a-8)2+64=-a2+16a,
所以u=f(a)=
答案:C
5.已知x0是函数f(x)=ex+2x-4的一个零点,若x1∈(-1,x0),x2∈(x0,2),则下列选项正确的是( )
A.f(x1)<0,f(x2)<0 B.f(x1)<0,f(x2)>0
C.f(x1)>0,f(x2)<0 D.f(x1)>0,f(x2)>0
解析:本题考查函数的单调性以及零点的概念,零点存在性定理的应用.∵f(0)=e0+2×0-4=-3<0,f(1)=e1+2×1-4=e-2>0,∴f(0)f(1)<0.又易知f(x)=ex+2x-4在R上是增函数,∴x0∈(0,1).根据f(x)的单调性,得f(x1)f(x0)=0,故选B.
答案:B
6.函数f(x)=3x-7+ln x的零点位于区间(n,n+1)(n∈N*)内,则n=( )
A.2 B.3
C.4 D.5
解析:设g(x)=ln x,h(x)=-3x+7,则函数g(x)和函数h(x)的图象交点的横坐标就是函数f(x)的零点.
在同一坐标系中画出函数g(x)和函数h(x)的图象,如图所示.
由图象知函数f(x)的零点属于区间,
又f(1)=-4<0,f(2)=-1+ln 2=ln <0,f(3)=2+ln 3>0,
所以函数f(x)的零点属于区间(2,3).所以n=2.
答案:A
二、填空题(本大题共4小题,每小题5分,共20分,把答案写在题中的横线上)
7.用二分法求函数y=f(x)在区间(2,4)上的近似解,验证f(2)·f(4)<0,给定精确度ε=0.01,取区间(2,4)的中点,x1==3.计算f(2)·f(x1)<0,则此时零点x0∈________(填区间).
解析:∵f(2)·f(4)<0,f(2)·f(3)<0,f(3)·f(4)>0,故x0∈(2,3).
答案:(2,3)
8.若函数f(x)=ax-x-a(a>0,且a≠1)有两个零点,则实数a的取值范围是____________.
解析:令ax-x-a=0即ax=x+a,若01,y=ax与y=x+a的图象如图所示.
答案:(1,+∞)
9.已知函数f(x)=logax+x-b(a>0,且a≠1).当2解析:∵2又∵log33>1,-1<3-b<0,∴f(3)>0,即f(2)f(3)<0,故x0∈(2,3),即n=2.
答案:2
10.一个容器装有细沙a cm3,细沙从容器底下一个细微的小孔慢慢地匀速漏出,t min后剩余的细沙量为y=ae-bt(cm3),经过8 min后发现容器内还有一半的沙子,则再经过________min,容器中的沙子只有开始时的八分之一.
解析:依题意有a·e-b×8=a,∴b=-,
∴y=a·e-·t若容器中只有开始时的八分之一,
则有a·e-·t=a,解得t=24,
所以再经过的时间为24-8=16 min.
答案:16
三、解答题(本大题共2小题,共25分,解答应写出文字说明,证明过程或演算步骤)
11.(本小题满分12分)某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上,该股票在30天内的日交易量Q(万股)与时间t(天)的部分数据如表所示:
第t天
4
10
16
22
Q(万股)
36
30
24
18
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据求出日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y表示该股票日交易额(万元),写出y关于t的函数关系式,并求在这30天中第几天日交易额最大,最大值是多少?
解:(1)P=(t∈N*).
(2)设Q=at+b(a,b为常数),把(4,36),(10,30)代入,
得解得
所以日交易量Q(万股)与时间t(天)的一次函数关系式为
Q=-t+40,0(3)由(1)(2)可得
y=(t∈N*)
即y= (t∈N*).
当0当20ymax<(20-60)2-40=120万元.
所以,在30天中的第15天,日交易额取得最大值125万元.
12.(本小题满分13分)设f(x)=log为奇函数,a为常数.
(1)求a的值;
(2)证明f(x)在区间(1,+∞)内单调递增;
(3)若对于区间[3,4]上的每一个x的值,不等式f(x)>x+m恒成立,求实数m的取值范围.
(1)解:∵f(-x)=-f(x),
∴log=-log=log.
∴=,即(1+ax)(1-ax)=-(x+1)(x-1),∴a=-1.
(2)证明:由(1)可知f(x)=log=log(x>1)记u(x)=1+,
由定义可证明u(x)在(1,+∞)上为减函数,
∴f(x)=log在(1,+∞)上为减函数.
(3)解:设g(x)=log-x,
则g(x)在[3,4]上为增函数.∴g(x)>m对x∈[3,4]恒成立,
∴m<g(3)=-.
(时间:45分钟 满分:75分)
一、选择题(本大题共6小题,每小题5分,共30分.在每小题给出的四个备选项中,只有一项是符合题目要求的)
1.已知f(x)=3ax+1-2a,设在(-1,1)上存在x0使f(x0)=0,则a的取值范围是( )
A.-1
C.a>或a<-1 D.a<-1
解析:∵f(x)是x的一次函数,
∴f(-1)·f(1)<0?a>或a<-1.
答案:C
2.某城市出租车起步价为10元,最长可租乘3 km(含3 km),以后每1 km为1.6元(不足1 km,按1 km计费),若出租车行驶在不需等待的公路上,则出租车的费用y(元)与行驶的里程x(km)之间的函数图象大致为( )
解析:由题意,当0
当n -1
3.已知函数f(x)=ax-3(a>0,且a≠1),f(x0)=0,若x0∈(0,1),则实数a的取值范围是( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,+∞)
解析:本题以函数零点为载体,考查指数函数、对数函数的图象和性质.由f(x0)=0,得ax0-3=0,
∴x0=loga3.又x0∈(0,1),∴0
答案:D
4.如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a米(0
解析:由题意设BC为x,则S=x·(16-x) .
其中: 所以a≤x≤12.
所以S=-x2+16x=-(x-8)2+64,x∈[a,12],
当a≤8时,u=f(8)=64.
当a>8时,u=f(a)=-(a-8)2+64=-a2+16a,
所以u=f(a)=
答案:C
5.已知x0是函数f(x)=ex+2x-4的一个零点,若x1∈(-1,x0),x2∈(x0,2),则下列选项正确的是( )
A.f(x1)<0,f(x2)<0 B.f(x1)<0,f(x2)>0
C.f(x1)>0,f(x2)<0 D.f(x1)>0,f(x2)>0
解析:本题考查函数的单调性以及零点的概念,零点存在性定理的应用.∵f(0)=e0+2×0-4=-3<0,f(1)=e1+2×1-4=e-2>0,∴f(0)f(1)<0.又易知f(x)=ex+2x-4在R上是增函数,∴x0∈(0,1).根据f(x)的单调性,得f(x1)
答案:B
6.函数f(x)=3x-7+ln x的零点位于区间(n,n+1)(n∈N*)内,则n=( )
A.2 B.3
C.4 D.5
解析:设g(x)=ln x,h(x)=-3x+7,则函数g(x)和函数h(x)的图象交点的横坐标就是函数f(x)的零点.
在同一坐标系中画出函数g(x)和函数h(x)的图象,如图所示.
由图象知函数f(x)的零点属于区间,
又f(1)=-4<0,f(2)=-1+ln 2=ln <0,f(3)=2+ln 3>0,
所以函数f(x)的零点属于区间(2,3).所以n=2.
答案:A
二、填空题(本大题共4小题,每小题5分,共20分,把答案写在题中的横线上)
7.用二分法求函数y=f(x)在区间(2,4)上的近似解,验证f(2)·f(4)<0,给定精确度ε=0.01,取区间(2,4)的中点,x1==3.计算f(2)·f(x1)<0,则此时零点x0∈________(填区间).
解析:∵f(2)·f(4)<0,f(2)·f(3)<0,f(3)·f(4)>0,故x0∈(2,3).
答案:(2,3)
8.若函数f(x)=ax-x-a(a>0,且a≠1)有两个零点,则实数a的取值范围是____________.
解析:令ax-x-a=0即ax=x+a,若0
答案:(1,+∞)
9.已知函数f(x)=logax+x-b(a>0,且a≠1).当2
答案:2
10.一个容器装有细沙a cm3,细沙从容器底下一个细微的小孔慢慢地匀速漏出,t min后剩余的细沙量为y=ae-bt(cm3),经过8 min后发现容器内还有一半的沙子,则再经过________min,容器中的沙子只有开始时的八分之一.
解析:依题意有a·e-b×8=a,∴b=-,
∴y=a·e-·t若容器中只有开始时的八分之一,
则有a·e-·t=a,解得t=24,
所以再经过的时间为24-8=16 min.
答案:16
三、解答题(本大题共2小题,共25分,解答应写出文字说明,证明过程或演算步骤)
11.(本小题满分12分)某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上,该股票在30天内的日交易量Q(万股)与时间t(天)的部分数据如表所示:
第t天
4
10
16
22
Q(万股)
36
30
24
18
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据求出日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y表示该股票日交易额(万元),写出y关于t的函数关系式,并求在这30天中第几天日交易额最大,最大值是多少?
解:(1)P=(t∈N*).
(2)设Q=at+b(a,b为常数),把(4,36),(10,30)代入,
得解得
所以日交易量Q(万股)与时间t(天)的一次函数关系式为
Q=-t+40,0
y=(t∈N*)
即y= (t∈N*).
当0
所以,在30天中的第15天,日交易额取得最大值125万元.
12.(本小题满分13分)设f(x)=log为奇函数,a为常数.
(1)求a的值;
(2)证明f(x)在区间(1,+∞)内单调递增;
(3)若对于区间[3,4]上的每一个x的值,不等式f(x)>x+m恒成立,求实数m的取值范围.
(1)解:∵f(-x)=-f(x),
∴log=-log=log.
∴=,即(1+ax)(1-ax)=-(x+1)(x-1),∴a=-1.
(2)证明:由(1)可知f(x)=log=log(x>1)记u(x)=1+,
由定义可证明u(x)在(1,+∞)上为减函数,
∴f(x)=log在(1,+∞)上为减函数.
(3)解:设g(x)=log-x,
则g(x)在[3,4]上为增函数.∴g(x)>m对x∈[3,4]恒成立,
∴m<g(3)=-.
