1.1.2 数列的函数特性
图片预览





文档简介
1.2 数列的函数特性
1.数列的概念是什么.
2.数列的通项公式的含义是什么.
3、递推公式?
对于数列中的每个序号n,都有唯一的一个数(项)an与之对应。
1 3 5 7 …… 2n-1
1
2
3
4
n
(自变量)
(函数值)
数列的实质:
结论:数列是一种特殊的函数.
6、数列的实质:
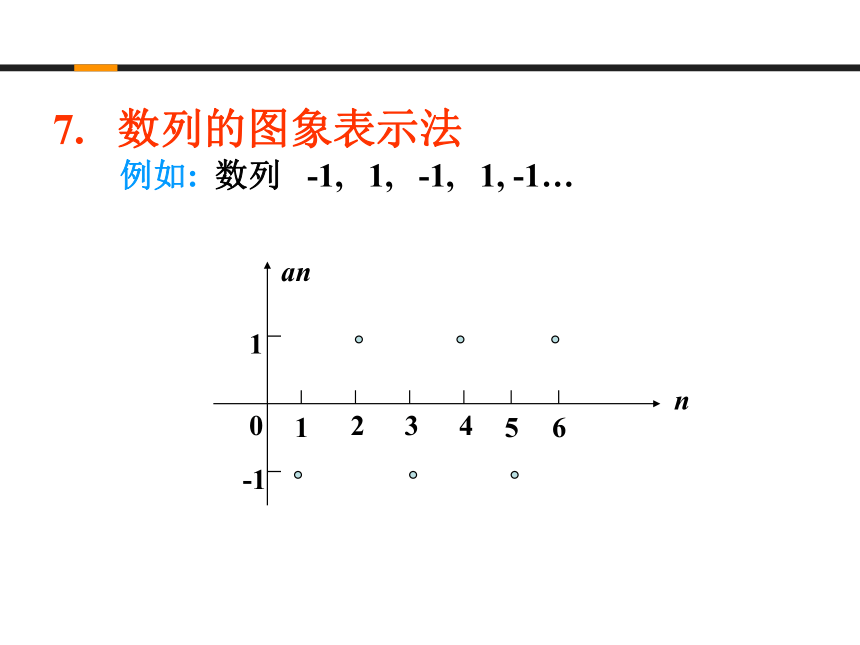
7. 数列的图象表示法
例如: 数列 -1, 1, -1, 1, -1…
1
0
-1
1
2
3
4
5
6
n
an
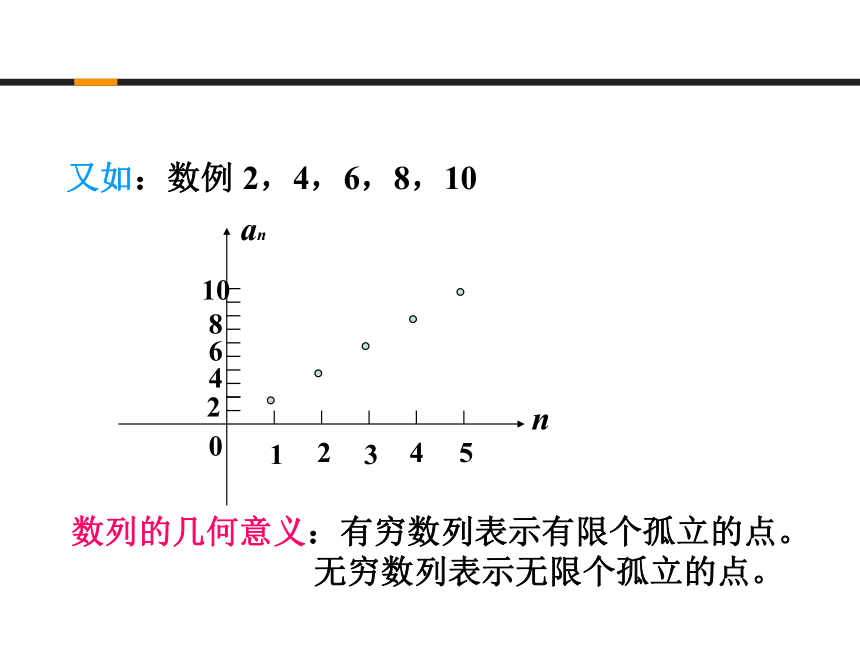
又如:数例 2,4,6,8,10
n
an
0
1
2
3
4
5
2
4
6
8
10
数列的几何意义:有穷数列表示有限个孤立的点。
无穷数列表示无限个孤立的点。
由上面的学习我们知道数列可以看作定义域为正整数集N+(或它的有限子集)的函数,当自变量从小到大依次取值时,该函数对应的一列函数值就是这个数列.
而数列的通项公式就类似于函数的解析式,因此研究数列的性质我们就可以借助数列的通项公式,而且数列的表示形式也和函数一样,有多种表示方法,下面来看几个例子.
新中国成立后,我国1952~1994年间部分年份进出口贸易总额(亿美元)数据排成一数列:
数列的函数特性
请看下面例子
19.4,31.0,42.5,45.9,147.5,381.4,696.0,1 154.4,2 367.3.
由上图可以看出我国1952~1994年部分年份,各时期进出口贸易总额的增长变化情况.
贸易总额/亿美元
年份/年
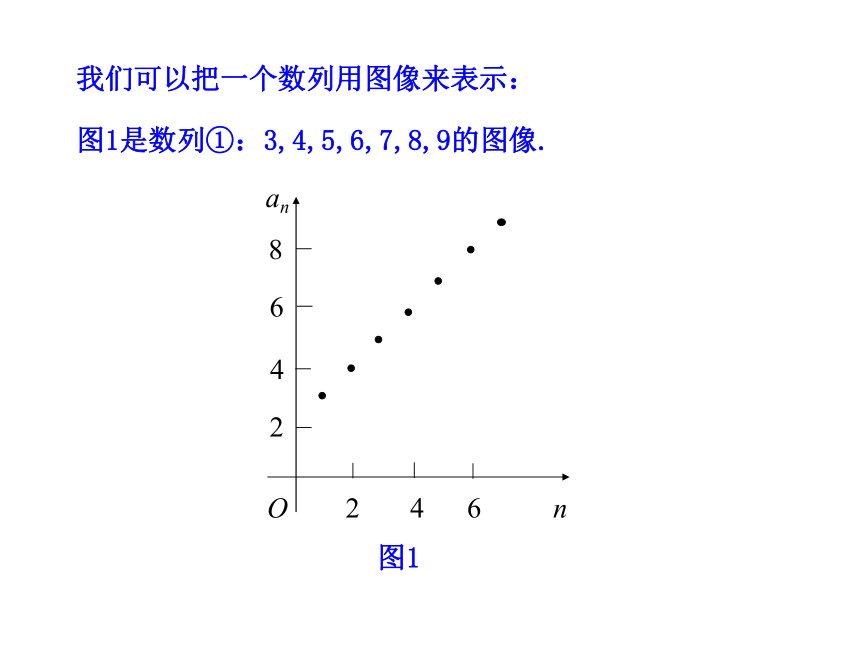
我们可以把一个数列用图像来表示:
图1是数列①:3,4,5,6,7,8,9的图像.
O 2 4 6 n
图3是数列⑥:2100,2100,2100,…,2100的图像.
思考:通过这几个例子你是否发现用图像来表示数列的好处.
从图中可以看出,数列①的函数图像上升,称这样的数列为递增数列;数列⑤的函数图像下降,称这样的数列为递减数列;数列⑥称为常数列.
思考:你是否能归纳一下递增数列、递减数列、常数列的概念呢?
一般地,一个数列{an},如果从第2项起,每一项都大于它前面的一项,即an+1> an,那么这个数列叫作递增数列.
如果从第2项起,每一项都小于它前面的一项,即an+1 如果数列{an}的各项都相等,那么这个数列叫作常数列.
例3 判断下列无穷数列的增减性.
解 图4是这个数列的图像,数列各项的值负正相间,表示数列的各点相对于横轴上下摆动,它既不是递增的,也不是递减的.
例5 一辆邮车每天从A地往B地运送邮件,沿途(包括A,B)共有8站,从A地出发时,装上发往后面7站的邮件各一个,到达后面各站后卸下前面各站发往该站的一个邮件,同时装上该站发往下面各站的邮件各一个.试写出邮件在各站装卸完毕后剩余邮件个数所成的数列,画出该数列的图像,并判断该数列的增减性.
解 将A,B之间所有站按序1,2,3,4,5,6,7,8编号,通过计算,上面各站剩余邮件数依次排成数列:
7,12,15,16,15,12,7,0.
填写下表
它在{1,2,3,4}上是递增的,在{4,5,6,7,8}上是递减的.
该数列的图像如下图所示.
可见,我们也可以用表格来表示数列.
站号 1 2 3 4 5 6 7 8
剩余邮件数 7 12 15 16 15 12 7 0
1.在1984年到2004年的6届夏季奥运会上,我国获得的金牌数依次排成数列:15,5,16,16,28,32.试画出该数列的图像.
2.判断下列数列
的增减性.
解:
(2)方法1:
所以数列
方法2:因为函数
为递减数列
是减函数且
是减函数,所以数列
为递减数列.
所以数列
既不是递增数列也不是递减数列,是摇摆数列.
本节课主要学习了:
1.递增数列、递减数列、常数列.
2.判断数列增减性的方法.
3.数列是一类定义域为正整数集的特殊函数,它也可以用图像、表格表示.
1.数列的概念是什么.
2.数列的通项公式的含义是什么.
3、递推公式?
对于数列中的每个序号n,都有唯一的一个数(项)an与之对应。
1 3 5 7 …… 2n-1
1
2
3
4
n
(自变量)
(函数值)
数列的实质:
结论:数列是一种特殊的函数.
6、数列的实质:
7. 数列的图象表示法
例如: 数列 -1, 1, -1, 1, -1…
1
0
-1
1
2
3
4
5
6
n
an
又如:数例 2,4,6,8,10
n
an
0
1
2
3
4
5
2
4
6
8
10
数列的几何意义:有穷数列表示有限个孤立的点。
无穷数列表示无限个孤立的点。
由上面的学习我们知道数列可以看作定义域为正整数集N+(或它的有限子集)的函数,当自变量从小到大依次取值时,该函数对应的一列函数值就是这个数列.
而数列的通项公式就类似于函数的解析式,因此研究数列的性质我们就可以借助数列的通项公式,而且数列的表示形式也和函数一样,有多种表示方法,下面来看几个例子.
新中国成立后,我国1952~1994年间部分年份进出口贸易总额(亿美元)数据排成一数列:
数列的函数特性
请看下面例子
19.4,31.0,42.5,45.9,147.5,381.4,696.0,1 154.4,2 367.3.
由上图可以看出我国1952~1994年部分年份,各时期进出口贸易总额的增长变化情况.
贸易总额/亿美元
年份/年
我们可以把一个数列用图像来表示:
图1是数列①:3,4,5,6,7,8,9的图像.
O 2 4 6 n
图3是数列⑥:2100,2100,2100,…,2100的图像.
思考:通过这几个例子你是否发现用图像来表示数列的好处.
从图中可以看出,数列①的函数图像上升,称这样的数列为递增数列;数列⑤的函数图像下降,称这样的数列为递减数列;数列⑥称为常数列.
思考:你是否能归纳一下递增数列、递减数列、常数列的概念呢?
一般地,一个数列{an},如果从第2项起,每一项都大于它前面的一项,即an+1> an,那么这个数列叫作递增数列.
如果从第2项起,每一项都小于它前面的一项,即an+1
例3 判断下列无穷数列的增减性.
解 图4是这个数列的图像,数列各项的值负正相间,表示数列的各点相对于横轴上下摆动,它既不是递增的,也不是递减的.
例5 一辆邮车每天从A地往B地运送邮件,沿途(包括A,B)共有8站,从A地出发时,装上发往后面7站的邮件各一个,到达后面各站后卸下前面各站发往该站的一个邮件,同时装上该站发往下面各站的邮件各一个.试写出邮件在各站装卸完毕后剩余邮件个数所成的数列,画出该数列的图像,并判断该数列的增减性.
解 将A,B之间所有站按序1,2,3,4,5,6,7,8编号,通过计算,上面各站剩余邮件数依次排成数列:
7,12,15,16,15,12,7,0.
填写下表
它在{1,2,3,4}上是递增的,在{4,5,6,7,8}上是递减的.
该数列的图像如下图所示.
可见,我们也可以用表格来表示数列.
站号 1 2 3 4 5 6 7 8
剩余邮件数 7 12 15 16 15 12 7 0
1.在1984年到2004年的6届夏季奥运会上,我国获得的金牌数依次排成数列:15,5,16,16,28,32.试画出该数列的图像.
2.判断下列数列
的增减性.
解:
(2)方法1:
所以数列
方法2:因为函数
为递减数列
是减函数且
是减函数,所以数列
为递减数列.
所以数列
既不是递增数列也不是递减数列,是摇摆数列.
本节课主要学习了:
1.递增数列、递减数列、常数列.
2.判断数列增减性的方法.
3.数列是一类定义域为正整数集的特殊函数,它也可以用图像、表格表示.
