3.1 用树状图或表格求概率同步课时作业(2)
文档属性
| 名称 | 3.1 用树状图或表格求概率同步课时作业(2) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-19 21:49:10 | ||
图片预览




文档简介
3.1 用树状图或表格求概率同步课时作业(2)
姓名:___________班级:___________考号:___________
一、选择题
1.不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,篮球有3个,第一次任意摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法,则两次摸到的都是白球的概率为(?????)
A. B. C. D.
2.小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )
A. B. C. D.
3.一个盒子装有除颜色外其它均相同的2个红球和3个白球,现从中任取1个球,则取到的是一个白球的概率为( )
A. B. C. D.
4.从1,2,﹣3三个数中,随机抽取两个数相乘,积是正数的概率是( )
A. 0 B. C. D. 1
5.把1枚质地均匀的普通硬币重复掷两次,落地后出现一次正面一次反面的概率是( )
A. 1 B. C. D.
6.我校举行A,B两项趣味比赛,甲、乙两名学生各自随机选择其中一项,则他们恰好参加同一项比赛的概率是( )
A. B. C. D.
7.一个不透明的袋子中有1个红球、2个黄球,这些球除颜色外无其他差别,从袋子中随机摸出1个球后放回,再随机摸出1个球,两次摸出的球都是黄球的概率( )
A. B. C. D.
8.在一个口袋中有3个完全相同的小球,把它们分别标号为1,2,3,从口袋中随机摸出一个小球记下标号后放回,再随机摸出一个小球记下标号,两次摸出小球的标号之和等于4的概率是
A. B. C. D.
二、填空题
9.网上购物已经成为人们常用的一种购物方式,售后评价也成为卖家和买家都关注的信息.消费者在网店购物后,将从“好评”、“中评”、“差评”中选择一种作为对卖家的评价,假设这三种评价是等可能的.若甲、乙两名消费者在某网店购买了同一商品,且都给出了评价,那么两人中至少有一个给“好评”的概率为__________.
10.某中学举行演讲比赛,经预赛,七、八年级各有一名同学进入决赛,九年级有两名同学进入决赛,九年级同学获得第一名的概率是_________.
11.小明有三件上衣,五条长裤,则他有_________种不同的穿法.
12.在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球l个,红球2个,摸出一个球不放回,再摸出—个球,两次都摸到红球的概率是________。
13.在﹣1、3、﹣2这三个数中,任选两个数的积作为k的值,使反比例函数的图象在第一、三象限的概率是_____.
14.李老师想从小明、小红、小丽和小亮四个人中用抽签的方式抽取两个人做流动值周生,则小红和小丽同时被抽中的概率是______.
15.甲盒中装有3个乒乓球,分别标号为1、2、3;乙盒中装有2个乒乓球,分别标号为1、2.现分别从每个盒中随机取出1个乒乓球,则取出的两个乒乓球的标号之和为4的概率是________________.
三、解答题
16.数学课上,李老师准备了四张背面看上去无差别的卡片A,B,C,D,每张卡片的正面标有字母a,b,c表示三条线段(如图),把四张卡片背面朝上放在桌面上,李老师从这四张卡片中随机抽取一张卡片后不放回,再随机抽取一张.
(1)用树状图或者列表表示所有可能出现的结果;
(2)求抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率.
17.某游乐场设计了一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A、B、C、D、E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的,并且规定:①玩家只能将小兔从A、B两个出入口放入,②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值8元小兔玩具,否则应付费5元.
(1)问游玩者得到小兔玩具的机会有多大?
(2)假设有100人次玩此游戏,估计游戏设计者可赚多少元?
18.在一副扑克牌中,拿出红桃2、红桃3、红桃4、红桃5四张牌,洗匀后,小明从中随机摸出一张,记下牌面上的数字为x,然后放回并洗匀,再由小华随机摸出一张,记下牌面上的数字为y,组成一对数(x,y).用列表法或树形图表示出(x,y)的所用可能出现的结果;求小明、小华各摸一次扑克牌所确定的一对数是方程x+y=5的解的概率.
19.一个不透明的袋子中装有大小、质地完全相同的3只球,球上分别标有2,3,5三个数字.
(1)从这个袋子中任意摸一只球,所标数字是奇数的概率是 ;
(2)从这个袋子中任意摸一只球,记下所标数字,不放回,再从这个袋子中任意摸只球,组成一个两位数,求所组成的两位数是5的倍数的概率.
20.为积极响应市委,市政府提出的“实现伟大中国梦,建设美丽鄂尔多斯”的号召,康巴什区某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
(1)扇形统计图中投稿篇数为3所对应的扇形的圆心角的度数是_____;该校八,九年级各班在这一周内投稿的平均篇数是______;并将该条形统计图补充完整.
(2)如果要求该校八、九年级的投稿班级个数为30个,估计投稿篇数为5篇的班级个数.
(3)在投稿篇数为9篇的4个班级中,八,九年级各有两个班,校学生会准备从这四个班级中选出两个班参加全市的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
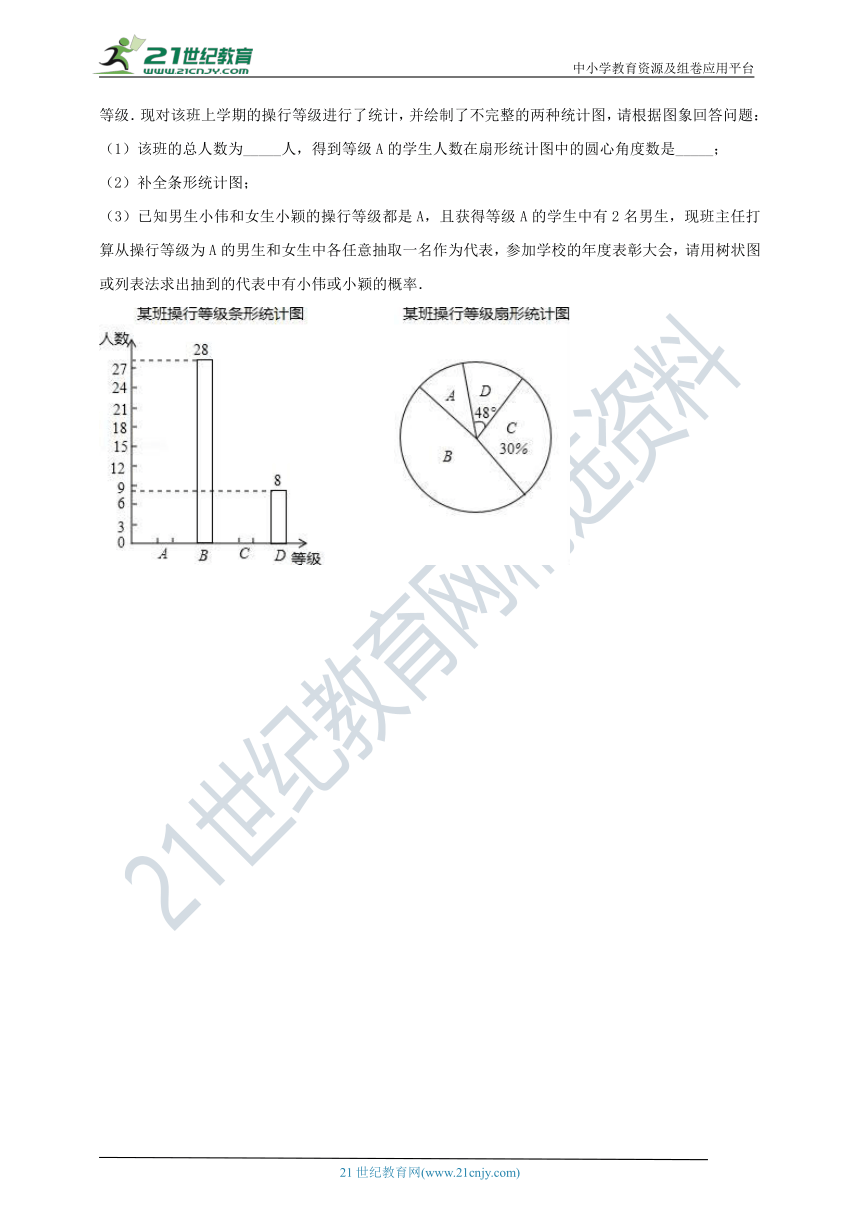
21.为规范学生的在校表现,某班实行了操行评分制,根据学生的操行分高低分为A、B、C、D四个等级.现对该班上学期的操行等级进行了统计,并绘制了不完整的两种统计图,请根据图象回答问题:
(1)该班的总人数为_____人,得到等级A的学生人数在扇形统计图中的圆心角度数是_____;
(2)补全条形统计图;
(3)已知男生小伟和女生小颖的操行等级都是A,且获得等级A的学生中有2名男生,现班主任打算从操行等级为A的男生和女生中各任意抽取一名作为代表,参加学校的年度表彰大会,请用树状图或列表法求出抽到的代表中有小伟或小颖的概率.
参考答案
1.A
【解析】分析:根据题意列出表格,然后根据概率的计算法则得出答案.
详解:根据题意列表可得:
白1
白2
黄
蓝1
蓝2
蓝3
白1
白1白2
白1黄
白1蓝1
白1蓝2
白1蓝3
白2
白2白1
白2黄
白2蓝1
白2蓝2
白2蓝3
黄
黄白1
黄
黄蓝1
黄蓝2
黄蓝3
蓝1
蓝1白1
蓝1
蓝1黄
蓝1蓝2
蓝1蓝3
蓝2
蓝2白1
蓝2
蓝2黄
蓝2蓝1
蓝2蓝3
蓝3
蓝3白1
蓝3
蓝3黄
蓝3蓝1
蓝3蓝2
∴P(都是白球)=,故选A.
点睛:本题主要考查的是概率的计算问题,属于基础题型.根据题意列出表格是解决这个问题的关键.
2.A
【解析】试题解析:分别记小明、小华选择“打扫社区卫生”为事件 ,小明、小华选择“参加社会调查”为事件 ,则两人的选择结果共有
这四种等可能的情况,其中符合条件的只有 这一种情况,故两人同时选择“参加社会调查”的概率为 .所以本题应选A.
3.C
【解析】首先根据题目已知条件画出树状图,由图不难得到共有20种等可能的结果,一个白球的有6种情况,结合概率公式,用取到的是一个白球的情况数除以所有的情况数即可解答.
本题解析:
画树状图,得
∵共有20种等可能的结果,取到的是一个白球的有6种情况,
∴取到的是一个白球的概率为:P==
故选C.
点睛:此题考查了概率的计算,需要掌握列举法(列表法或树状图法)求概率的方法;通过画树状图或列表得到所有等可能的结果,并确定取到的是一个白球的结果数;再利用概率的计算公式,用取到的是一个白球的结果数除以所有等可能的结果数即可.
4.B
【解析】画树状图得:
∵共有6种等可能的结果,随机抽取两个数相乘,积是正数的有2种情况,
∴随机抽取两个数相乘,积是正数的概率是: ;
故选B。
【点睛】画树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比。
5.B
【解析】解:列表如下:
正
反
正
(正,正)
(反,正)
反
(正,反)
(反,反)
所有等可能的情况有4种,其中一次正面一次反面的情况数为2种,
则P= .
故选:B.
6.C
【解析】画树状图得:
∵共有4种等可能的结果,他们恰好参加同一项比赛的有2种情况, ∴他们恰好参加同一项比赛的概率是: .
故选C.
【点睛】用列表法或树状图法求概率:注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.
7.D
【解析】
【详解】
画树状图为:
共有9种等可能的结果,其中两次摸出的球都是黄球的情况为4,
所以两次摸出的球都是黄球的概率为.
故选D.
【点睛】
本题考查画树状图法求概率,当一次试验涉及三个或更多个因素时,我们可以先画出其树状图,再运用公式P(A)=计算概率.
8.A
【解析】
【分析】
先根据画树形图得到所有可能出现的结果,再根据概率公式即可求得结果.
【详解】
由题意画树形图如下:
则所有可能出现的结果共有9个,这些结果出现的可能性相等,标号之和等于4的结果共有3种.?????
所以P(标号之和等于4)=.
故选:A
【点睛】
此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.
9.
【解析】
【分析】
画树状图展开所有9种等可能的结果数,再找出两个中至少有一个给“好评”的结果数,然后根据概率公式求解.
【详解】
画树状图为:
共有9种等可能的结果数,其中两人中至少有一个给“好评”的结果数为5,
所以两人中至少有一个给“好评”的概率为.
故答案为:.
【点睛】
本题考查了列表法与树状图法:利用列表法或树状图法展开所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.
10.
【解析】根据题意列表如下:
第1名 第2名
七
八
九1
九2
七
(七,八)
(七,九1)
(七,九2)
八
(八,七)
(八,九1)
(八,九2)
九1
(九1,七)
(九1,八)
(九1,九2)
九2
(九2,七)
(九2,八)
(九2,九1)
所有等可能的情况有12种,其中九年级同学获得第一名的情况有6种,
则P==.
故答案为.
11.15
【解析】画树状图:
有15中穿法.
故答案为15.
点睛:掌握画树状图解决问题的方法.
12.
【解析】分析:画树状图写出所有的情况,根据概率的求法计算概率.
详解:
∴一共有12种情况,有2种情况两次都摸到红球,
∴两次都摸到红球的概率是
故答案为:
点睛:考查概率的计算,明确概率的意义是解题的关键,概率等于所求情况数与总情况数的比.
13.
【解析】画树状图得:
∵共有6种等可能的结果,任选两个数的积作为k的值,使反比例函数的图象在第一、三象限的有2种情况,
∴任选两个数的积作为k的值,使反比例函数的图象在第一、三象限的概率是:.
故答案为:.
14.
【解析】
【分析】
首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小红和小丽同时被抽中的情况,再利用概率公式即可求得答案.
【详解】
画树状图得: ∵共有12种等可能的结果,小红和小丽同时被抽中的有2种情况, ∴小红和小丽同时被抽中的概率是:P =.
故答案为:
【点睛】
此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
15.
【解析】
【分析】
首先根据题意作出树状图,然后由树状图求得所有等可能的结果与取出的两球标号之和为4的情况,再利用概率公式求解即可求得答案.
【详解】
画树状图得:
∵共有6种等可能的结果,取出的两球标号之和为4的有2种情况,
∴取出的两球标号之和为4的概率是:.
故答案为:.
【点睛】
此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.
16.(1)用树状图表示见解析;(2)抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率为.
【解析】
【分析】
(1)依据题意先用列表法或画树状图法分析所有等可能的出现结果;
(2)由四张卡片中只有C、D两张卡片能构成三角形,据此利用概率公式求解可得.
【详解】
解:(1)由题意可得,
共有12种等可能的结果;
(2)∵共有12种等可能结果,其中抽取的两张卡片中每张卡片上的三条线段都能组成三角形有2种结果,
∴抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率为.
【点睛】
本题考查树状图的运用,注意作图列表时按一定的顺序,做到不重不漏.用到的知识点为:概率=所求情况数与总情况数之比.
17.(1)游玩者玩一次“守株待兔”游戏能得到小兔玩具的机会是;(2)估计游戏设计者可赚240元.
【解析】分析:(1)首先我们要确定入口为A、B,而出口却有A、B、C、D、E共5个,由此画出树状图或表格;而游玩者得到小兔玩具只有出口与入口对应,即A-A,B-B这种情况,利用概率公式可以算出对应的概率,即游玩者得到小兔玩具的机会;
(2)通过总数与概率相乘可以得到获得奖品的人数,再结合获奖与不获奖的所支付的金额,可以算出游戏设计者的纯利润.
详解:(1)画树状图为:
共有10种等可能的结果数,其中从开始进入的出入口离开的结果数为2,
所以游玩者玩一次“守株待兔”游戏能得到小兔玩具的概率==;
(2)100×0.8×5﹣100×0. 2×8=240,所以估计游戏设计者可赚240元.
点睛:本题主要考查概率的计算,熟练掌握列表法或画树状图是解答本题的关键. 概率的计算公式是用符合条件的情况数m除以所有等可能发生的情况数n即可,即.
18.(1)见表;(2)
【解析】
【分析】
依据题意先用列表法或画树状图法分析所有等可能的出现结果,从数对中找出方程x+y=5的解,然后根据概率公式求出该事件的概率即可解答.
【详解】
列表得:
红桃2
红桃3
红桃4
红桃5
红桃2
2,2
2,3
2,4
2,5
红桃3
3,2
3,3
3,4
3,5
红桃4
4,2
4,3
4,4
4,5
红桃5
5,2
5,3
5,4
5,5
观察表格可知一共有16种可能出现的结果;
其中满足x+y=5有的两种,所以P(和等于5)=.
【点睛】
本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
19.(1);(2).
【解析】
【分析】
(1)用直接列举法即可求得概率;
(2)利用画树状图的方法即可求得概率.
【详解】
(1)∵在球上分别标有2,3,5三个数字的小球中,奇数有3、5这两个,
∴从这个袋子中任意摸一只球,所标数字是奇数的概率是,
故答案为:;
(2)如图所示:
共有6种情况,其中是5的倍数的有25,35两种情况,
所组成的两位数是5的倍数的概率为=.
【点睛】
本题考查用直接列举法和画树状图法求概率,当事件涉及的对象比较单一且出现的等可能结果数目比较少时适合使用直接列举法求概率;当一次试验涉及三个或更多个因素时适合使用画树状图法求概率.
20.30°6篇
【解析】
【分析】
(1)根据扇形图和柱状图寻求联系,其中周角是360°.(2)利用百分比计算.(3)根据题意绘制树状图,计算概率.
【详解】
(1)投稿班级的总个数为:3÷25%=12(个),
∴×360°=30°.
∵投稿5篇的班级有12﹣1﹣2﹣3﹣4=2(个),
∴各班在这一周内投稿的平均篇数为×(2+3×2+5×2+6×3+9×4)=×72=6(篇),
该条形统计图补充完整为:
故答案为:30°,6篇;
(2)30××100%=5(个);
(3)画树状图如下:
总共12画树状图如下:
总共12种情况,不在同一年级的有8种情况,
所选两个班正好不在同一年级的概率为: =.
【点睛】
(1)利用频率估算法:大量重复试验中,事件A发生的频率会稳定在某个常数p附近,那么这个常数P就叫做事件A的概率(有些时候用计算出A发生的所有频率的平均值作为其概率).
(2)定义法:如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,考察事件A包含其中的m中结果,那么事件A发生的概率为P.
(3)列表法:当一次试验要设计两个因素,可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法.其中一个因素作为行标,另一个因素作为列标.
(4)树状图法:当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
21. (1)60 ,36°;(2)答案见解析;(3).
【解析】
【分析】
(1)该班的总人数=D级人数÷对应的百分比,得到等级A的学生人数在扇形统计图中的圆心角度数;
(2)利用A,C级的人数补全条形统计图;
(3)根据概率公式解答即可.
【详解】
(1)该班的总人数为8÷=60(人),得到等级A的学生人数为60﹣28﹣8﹣60×30%=6(人)
得到等级A的学生人数在扇形统计图中的圆心角度数是×360°=36°.
故答案为:60,36°.
(2)如图:
(3)得A的总人数为6人,其中2男4女,假设男1为小伟,女1为小颖.
一共有8种情况,抽到的代表中有小伟或小颖的共5种情况,所以,P(小伟或小颖)=.
【点睛】
本题主要考查了条形统计图,圆形统计图及树状图列举法,解题的关键是概率=所求情况数与总情况数之比.
姓名:___________班级:___________考号:___________
一、选择题
1.不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,篮球有3个,第一次任意摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法,则两次摸到的都是白球的概率为(?????)
A. B. C. D.
2.小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )
A. B. C. D.
3.一个盒子装有除颜色外其它均相同的2个红球和3个白球,现从中任取1个球,则取到的是一个白球的概率为( )
A. B. C. D.
4.从1,2,﹣3三个数中,随机抽取两个数相乘,积是正数的概率是( )
A. 0 B. C. D. 1
5.把1枚质地均匀的普通硬币重复掷两次,落地后出现一次正面一次反面的概率是( )
A. 1 B. C. D.
6.我校举行A,B两项趣味比赛,甲、乙两名学生各自随机选择其中一项,则他们恰好参加同一项比赛的概率是( )
A. B. C. D.
7.一个不透明的袋子中有1个红球、2个黄球,这些球除颜色外无其他差别,从袋子中随机摸出1个球后放回,再随机摸出1个球,两次摸出的球都是黄球的概率( )
A. B. C. D.
8.在一个口袋中有3个完全相同的小球,把它们分别标号为1,2,3,从口袋中随机摸出一个小球记下标号后放回,再随机摸出一个小球记下标号,两次摸出小球的标号之和等于4的概率是
A. B. C. D.
二、填空题
9.网上购物已经成为人们常用的一种购物方式,售后评价也成为卖家和买家都关注的信息.消费者在网店购物后,将从“好评”、“中评”、“差评”中选择一种作为对卖家的评价,假设这三种评价是等可能的.若甲、乙两名消费者在某网店购买了同一商品,且都给出了评价,那么两人中至少有一个给“好评”的概率为__________.
10.某中学举行演讲比赛,经预赛,七、八年级各有一名同学进入决赛,九年级有两名同学进入决赛,九年级同学获得第一名的概率是_________.
11.小明有三件上衣,五条长裤,则他有_________种不同的穿法.
12.在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球l个,红球2个,摸出一个球不放回,再摸出—个球,两次都摸到红球的概率是________。
13.在﹣1、3、﹣2这三个数中,任选两个数的积作为k的值,使反比例函数的图象在第一、三象限的概率是_____.
14.李老师想从小明、小红、小丽和小亮四个人中用抽签的方式抽取两个人做流动值周生,则小红和小丽同时被抽中的概率是______.
15.甲盒中装有3个乒乓球,分别标号为1、2、3;乙盒中装有2个乒乓球,分别标号为1、2.现分别从每个盒中随机取出1个乒乓球,则取出的两个乒乓球的标号之和为4的概率是________________.
三、解答题
16.数学课上,李老师准备了四张背面看上去无差别的卡片A,B,C,D,每张卡片的正面标有字母a,b,c表示三条线段(如图),把四张卡片背面朝上放在桌面上,李老师从这四张卡片中随机抽取一张卡片后不放回,再随机抽取一张.
(1)用树状图或者列表表示所有可能出现的结果;
(2)求抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率.
17.某游乐场设计了一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有A、B、C、D、E五个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的,并且规定:①玩家只能将小兔从A、B两个出入口放入,②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值8元小兔玩具,否则应付费5元.
(1)问游玩者得到小兔玩具的机会有多大?
(2)假设有100人次玩此游戏,估计游戏设计者可赚多少元?
18.在一副扑克牌中,拿出红桃2、红桃3、红桃4、红桃5四张牌,洗匀后,小明从中随机摸出一张,记下牌面上的数字为x,然后放回并洗匀,再由小华随机摸出一张,记下牌面上的数字为y,组成一对数(x,y).用列表法或树形图表示出(x,y)的所用可能出现的结果;求小明、小华各摸一次扑克牌所确定的一对数是方程x+y=5的解的概率.
19.一个不透明的袋子中装有大小、质地完全相同的3只球,球上分别标有2,3,5三个数字.
(1)从这个袋子中任意摸一只球,所标数字是奇数的概率是 ;
(2)从这个袋子中任意摸一只球,记下所标数字,不放回,再从这个袋子中任意摸只球,组成一个两位数,求所组成的两位数是5的倍数的概率.
20.为积极响应市委,市政府提出的“实现伟大中国梦,建设美丽鄂尔多斯”的号召,康巴什区某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
(1)扇形统计图中投稿篇数为3所对应的扇形的圆心角的度数是_____;该校八,九年级各班在这一周内投稿的平均篇数是______;并将该条形统计图补充完整.
(2)如果要求该校八、九年级的投稿班级个数为30个,估计投稿篇数为5篇的班级个数.
(3)在投稿篇数为9篇的4个班级中,八,九年级各有两个班,校学生会准备从这四个班级中选出两个班参加全市的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
21.为规范学生的在校表现,某班实行了操行评分制,根据学生的操行分高低分为A、B、C、D四个等级.现对该班上学期的操行等级进行了统计,并绘制了不完整的两种统计图,请根据图象回答问题:
(1)该班的总人数为_____人,得到等级A的学生人数在扇形统计图中的圆心角度数是_____;
(2)补全条形统计图;
(3)已知男生小伟和女生小颖的操行等级都是A,且获得等级A的学生中有2名男生,现班主任打算从操行等级为A的男生和女生中各任意抽取一名作为代表,参加学校的年度表彰大会,请用树状图或列表法求出抽到的代表中有小伟或小颖的概率.
参考答案
1.A
【解析】分析:根据题意列出表格,然后根据概率的计算法则得出答案.
详解:根据题意列表可得:
白1
白2
黄
蓝1
蓝2
蓝3
白1
白1白2
白1黄
白1蓝1
白1蓝2
白1蓝3
白2
白2白1
白2黄
白2蓝1
白2蓝2
白2蓝3
黄
黄白1
黄
黄蓝1
黄蓝2
黄蓝3
蓝1
蓝1白1
蓝1
蓝1黄
蓝1蓝2
蓝1蓝3
蓝2
蓝2白1
蓝2
蓝2黄
蓝2蓝1
蓝2蓝3
蓝3
蓝3白1
蓝3
蓝3黄
蓝3蓝1
蓝3蓝2
∴P(都是白球)=,故选A.
点睛:本题主要考查的是概率的计算问题,属于基础题型.根据题意列出表格是解决这个问题的关键.
2.A
【解析】试题解析:分别记小明、小华选择“打扫社区卫生”为事件 ,小明、小华选择“参加社会调查”为事件 ,则两人的选择结果共有
这四种等可能的情况,其中符合条件的只有 这一种情况,故两人同时选择“参加社会调查”的概率为 .所以本题应选A.
3.C
【解析】首先根据题目已知条件画出树状图,由图不难得到共有20种等可能的结果,一个白球的有6种情况,结合概率公式,用取到的是一个白球的情况数除以所有的情况数即可解答.
本题解析:
画树状图,得
∵共有20种等可能的结果,取到的是一个白球的有6种情况,
∴取到的是一个白球的概率为:P==
故选C.
点睛:此题考查了概率的计算,需要掌握列举法(列表法或树状图法)求概率的方法;通过画树状图或列表得到所有等可能的结果,并确定取到的是一个白球的结果数;再利用概率的计算公式,用取到的是一个白球的结果数除以所有等可能的结果数即可.
4.B
【解析】画树状图得:
∵共有6种等可能的结果,随机抽取两个数相乘,积是正数的有2种情况,
∴随机抽取两个数相乘,积是正数的概率是: ;
故选B。
【点睛】画树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比。
5.B
【解析】解:列表如下:
正
反
正
(正,正)
(反,正)
反
(正,反)
(反,反)
所有等可能的情况有4种,其中一次正面一次反面的情况数为2种,
则P= .
故选:B.
6.C
【解析】画树状图得:
∵共有4种等可能的结果,他们恰好参加同一项比赛的有2种情况, ∴他们恰好参加同一项比赛的概率是: .
故选C.
【点睛】用列表法或树状图法求概率:注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.
7.D
【解析】
【详解】
画树状图为:
共有9种等可能的结果,其中两次摸出的球都是黄球的情况为4,
所以两次摸出的球都是黄球的概率为.
故选D.
【点睛】
本题考查画树状图法求概率,当一次试验涉及三个或更多个因素时,我们可以先画出其树状图,再运用公式P(A)=计算概率.
8.A
【解析】
【分析】
先根据画树形图得到所有可能出现的结果,再根据概率公式即可求得结果.
【详解】
由题意画树形图如下:
则所有可能出现的结果共有9个,这些结果出现的可能性相等,标号之和等于4的结果共有3种.?????
所以P(标号之和等于4)=.
故选:A
【点睛】
此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.
9.
【解析】
【分析】
画树状图展开所有9种等可能的结果数,再找出两个中至少有一个给“好评”的结果数,然后根据概率公式求解.
【详解】
画树状图为:
共有9种等可能的结果数,其中两人中至少有一个给“好评”的结果数为5,
所以两人中至少有一个给“好评”的概率为.
故答案为:.
【点睛】
本题考查了列表法与树状图法:利用列表法或树状图法展开所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.
10.
【解析】根据题意列表如下:
第1名 第2名
七
八
九1
九2
七
(七,八)
(七,九1)
(七,九2)
八
(八,七)
(八,九1)
(八,九2)
九1
(九1,七)
(九1,八)
(九1,九2)
九2
(九2,七)
(九2,八)
(九2,九1)
所有等可能的情况有12种,其中九年级同学获得第一名的情况有6种,
则P==.
故答案为.
11.15
【解析】画树状图:
有15中穿法.
故答案为15.
点睛:掌握画树状图解决问题的方法.
12.
【解析】分析:画树状图写出所有的情况,根据概率的求法计算概率.
详解:
∴一共有12种情况,有2种情况两次都摸到红球,
∴两次都摸到红球的概率是
故答案为:
点睛:考查概率的计算,明确概率的意义是解题的关键,概率等于所求情况数与总情况数的比.
13.
【解析】画树状图得:
∵共有6种等可能的结果,任选两个数的积作为k的值,使反比例函数的图象在第一、三象限的有2种情况,
∴任选两个数的积作为k的值,使反比例函数的图象在第一、三象限的概率是:.
故答案为:.
14.
【解析】
【分析】
首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小红和小丽同时被抽中的情况,再利用概率公式即可求得答案.
【详解】
画树状图得: ∵共有12种等可能的结果,小红和小丽同时被抽中的有2种情况, ∴小红和小丽同时被抽中的概率是:P =.
故答案为:
【点睛】
此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
15.
【解析】
【分析】
首先根据题意作出树状图,然后由树状图求得所有等可能的结果与取出的两球标号之和为4的情况,再利用概率公式求解即可求得答案.
【详解】
画树状图得:
∵共有6种等可能的结果,取出的两球标号之和为4的有2种情况,
∴取出的两球标号之和为4的概率是:.
故答案为:.
【点睛】
此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.
16.(1)用树状图表示见解析;(2)抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率为.
【解析】
【分析】
(1)依据题意先用列表法或画树状图法分析所有等可能的出现结果;
(2)由四张卡片中只有C、D两张卡片能构成三角形,据此利用概率公式求解可得.
【详解】
解:(1)由题意可得,
共有12种等可能的结果;
(2)∵共有12种等可能结果,其中抽取的两张卡片中每张卡片上的三条线段都能组成三角形有2种结果,
∴抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率为.
【点睛】
本题考查树状图的运用,注意作图列表时按一定的顺序,做到不重不漏.用到的知识点为:概率=所求情况数与总情况数之比.
17.(1)游玩者玩一次“守株待兔”游戏能得到小兔玩具的机会是;(2)估计游戏设计者可赚240元.
【解析】分析:(1)首先我们要确定入口为A、B,而出口却有A、B、C、D、E共5个,由此画出树状图或表格;而游玩者得到小兔玩具只有出口与入口对应,即A-A,B-B这种情况,利用概率公式可以算出对应的概率,即游玩者得到小兔玩具的机会;
(2)通过总数与概率相乘可以得到获得奖品的人数,再结合获奖与不获奖的所支付的金额,可以算出游戏设计者的纯利润.
详解:(1)画树状图为:
共有10种等可能的结果数,其中从开始进入的出入口离开的结果数为2,
所以游玩者玩一次“守株待兔”游戏能得到小兔玩具的概率==;
(2)100×0.8×5﹣100×0. 2×8=240,所以估计游戏设计者可赚240元.
点睛:本题主要考查概率的计算,熟练掌握列表法或画树状图是解答本题的关键. 概率的计算公式是用符合条件的情况数m除以所有等可能发生的情况数n即可,即.
18.(1)见表;(2)
【解析】
【分析】
依据题意先用列表法或画树状图法分析所有等可能的出现结果,从数对中找出方程x+y=5的解,然后根据概率公式求出该事件的概率即可解答.
【详解】
列表得:
红桃2
红桃3
红桃4
红桃5
红桃2
2,2
2,3
2,4
2,5
红桃3
3,2
3,3
3,4
3,5
红桃4
4,2
4,3
4,4
4,5
红桃5
5,2
5,3
5,4
5,5
观察表格可知一共有16种可能出现的结果;
其中满足x+y=5有的两种,所以P(和等于5)=.
【点睛】
本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
19.(1);(2).
【解析】
【分析】
(1)用直接列举法即可求得概率;
(2)利用画树状图的方法即可求得概率.
【详解】
(1)∵在球上分别标有2,3,5三个数字的小球中,奇数有3、5这两个,
∴从这个袋子中任意摸一只球,所标数字是奇数的概率是,
故答案为:;
(2)如图所示:
共有6种情况,其中是5的倍数的有25,35两种情况,
所组成的两位数是5的倍数的概率为=.
【点睛】
本题考查用直接列举法和画树状图法求概率,当事件涉及的对象比较单一且出现的等可能结果数目比较少时适合使用直接列举法求概率;当一次试验涉及三个或更多个因素时适合使用画树状图法求概率.
20.30°6篇
【解析】
【分析】
(1)根据扇形图和柱状图寻求联系,其中周角是360°.(2)利用百分比计算.(3)根据题意绘制树状图,计算概率.
【详解】
(1)投稿班级的总个数为:3÷25%=12(个),
∴×360°=30°.
∵投稿5篇的班级有12﹣1﹣2﹣3﹣4=2(个),
∴各班在这一周内投稿的平均篇数为×(2+3×2+5×2+6×3+9×4)=×72=6(篇),
该条形统计图补充完整为:
故答案为:30°,6篇;
(2)30××100%=5(个);
(3)画树状图如下:
总共12画树状图如下:
总共12种情况,不在同一年级的有8种情况,
所选两个班正好不在同一年级的概率为: =.
【点睛】
(1)利用频率估算法:大量重复试验中,事件A发生的频率会稳定在某个常数p附近,那么这个常数P就叫做事件A的概率(有些时候用计算出A发生的所有频率的平均值作为其概率).
(2)定义法:如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,考察事件A包含其中的m中结果,那么事件A发生的概率为P.
(3)列表法:当一次试验要设计两个因素,可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法.其中一个因素作为行标,另一个因素作为列标.
(4)树状图法:当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
21. (1)60 ,36°;(2)答案见解析;(3).
【解析】
【分析】
(1)该班的总人数=D级人数÷对应的百分比,得到等级A的学生人数在扇形统计图中的圆心角度数;
(2)利用A,C级的人数补全条形统计图;
(3)根据概率公式解答即可.
【详解】
(1)该班的总人数为8÷=60(人),得到等级A的学生人数为60﹣28﹣8﹣60×30%=6(人)
得到等级A的学生人数在扇形统计图中的圆心角度数是×360°=36°.
故答案为:60,36°.
(2)如图:
(3)得A的总人数为6人,其中2男4女,假设男1为小伟,女1为小颖.
一共有8种情况,抽到的代表中有小伟或小颖的共5种情况,所以,P(小伟或小颖)=.
【点睛】
本题主要考查了条形统计图,圆形统计图及树状图列举法,解题的关键是概率=所求情况数与总情况数之比.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
