(粤教版选修3-2)物理:1.5《法拉第电磁感应定律的应用(一)》课件
文档属性
| 名称 | (粤教版选修3-2)物理:1.5《法拉第电磁感应定律的应用(一)》课件 |  | |
| 格式 | rar | ||
| 文件大小 | 70.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 广东版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2010-09-07 08:36:00 | ||
图片预览





文档简介
课件18张PPT。法拉第电磁感应定律的应用(一)
一、感应电动势 1.感应电动势:在电磁感应现象中产生的电动势叫做感应电动势,产生感应电动势的那部分导体相当于电源.
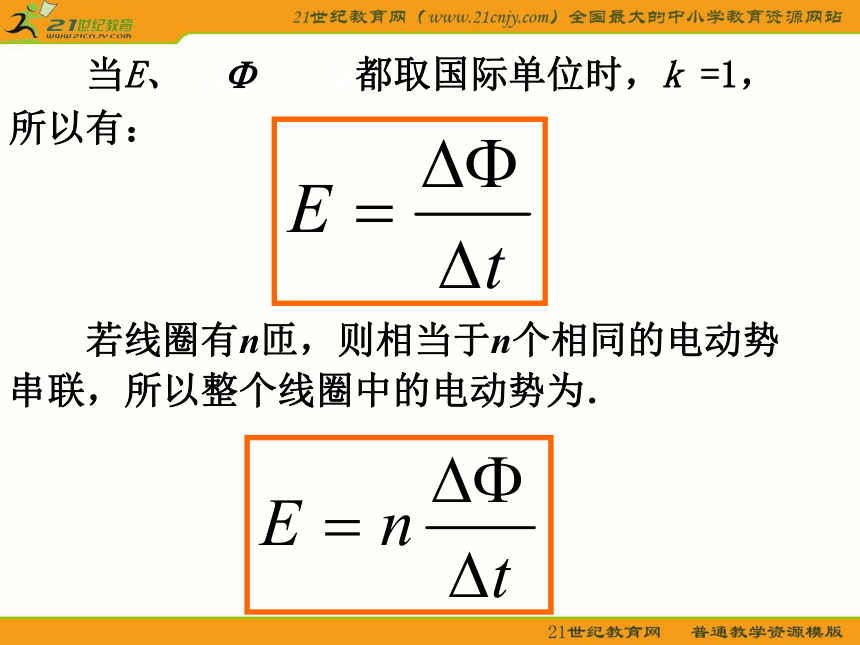
2.感应电动势与感应电流:感应电动势是形成感应电流的必要条件,有感应电动势不一定存在感应电流(要看电路是否闭合),有感应电流一定存在感应电动势. 2.法拉第电磁感应定律:电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比. 当E、 ?? 、 ?t都取国际单位时,k =1,
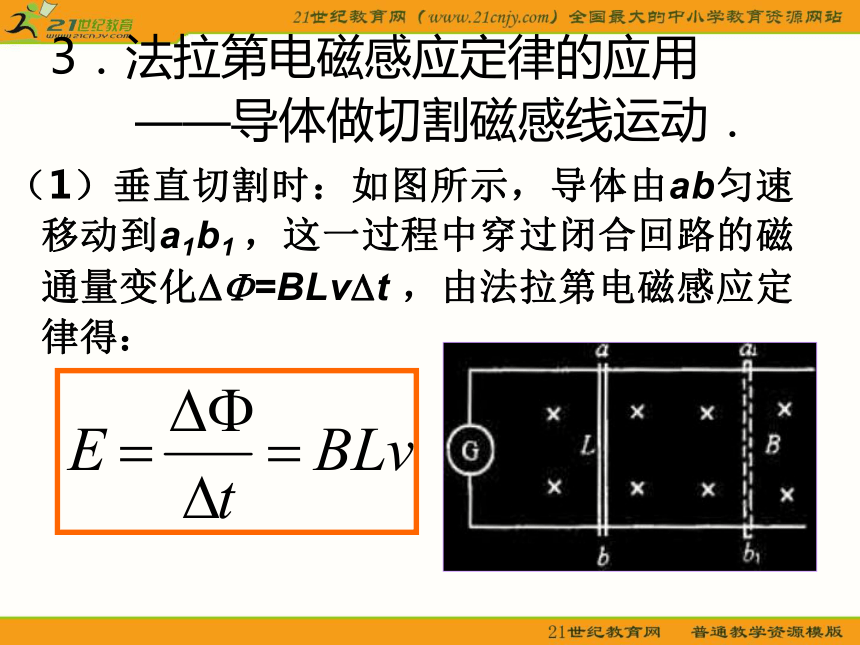
所以有: 若线圈有n匝,则相当于n个相同的电动势串联,所以整个线圈中的电动势为.3.法拉第电磁感应定律的应用 ——导体做切割磁感线运动. (1)垂直切割时:如图所示,导体由ab匀速移动到a1b1 ,这一过程中穿过闭合回路的磁通量变化??=BLv?t ,由法拉第电磁感应定律得: (2)切割方向与磁场方向成角时:如图所示,将v分解为垂直B和平行B的两个分量,其中:所以可知:导线切割磁感线时产生的电动势的大小,跟磁感强度B、导线长度L、运动速度v以及运动方向与磁感线方向的夹角的正弦sin?成正比例题1: 长为L的金属棒ab,绕b端在垂直于匀强磁场的平面内以角速度匀速转动,磁感应强度为B,如图所示,求ab两端的电势差.解析: ab两端电势差等于金属棒切割磁感线产生的电动势(因为没有外电路),所以只要求出电动势即可.棒上各处速率不等,不能直接用E=BLv来求,但棒上各点的速度v=? r与半径成正比,因此可用棒的中点速度作为平均切割速度代入公式计算:例题2、如下图所示,半径为r的金属环绕通过某直径的轴OO’以角速度ω作匀速转动,匀强磁场的磁感应强度为B,从金属环面与磁场方向重合时开始计时,则在金属环转过30°角的过程中,环中产生的电动势的平均值是多大?分析:根据金属环在磁场中转动的始末位置穿过环的磁通量Φ1和Φ2以及完成这一变化所用时间△t,就可以求出环中产生的感应电动势 .例题3、如图所示把线框abcd从磁感应强度为的匀强磁场中匀速拉出,速度方向与ab边垂直向右,速度的大小为v,线圈的边长为L,每边的电阻为r,问,线圈在运动过程中,ab两点的电势差为多少?当线框abcd 整个在磁场的时候,穿过线圈的磁通量不变,无感应电流,ab和cd两边切割磁感线,等效电路图如图2所示:
Uab=E=BLv
当cd边离开磁场,ab边切割磁感线,ad,bc,cd边的电阻属于外阻,等效电路图如图3所示:
Uab=E-Ir=BLv-Ir 当线框abcd 整个在磁场的时候:Uab=E=BLv
当cd 边离开磁场的时候:Uab =3BLv/4 电动式发电式阻尼式一、单棒问题运动特点最终特征a逐渐减小的减速运动静止a逐渐减小的加速运动匀速a逐渐减小的加速运动匀速基本模型I=0 (或恒定)I 恒定I=0画等效电路二、含容式单棒问题放电式无外力充电式运动特点最终特征基本模型有外力充电式a逐渐减小的加速运动匀速运动I=0a逐渐减小的减速运动匀速运动I=0匀加速运动匀加速运动I 恒定三、无外力双棒问题运动特点最终特征基本模型杆1做a渐小的加速运动杆2做a渐小的减速运动v1=v2I=0无外力等距式杆1做a渐小的减速运动杆2做a渐小的加速运动无外力 不等距式a=0I=0L1v1=L2v2四、有外力双棒问题运动特点最终特征基本模型有外力 不等距式杆1做a渐小的加速运动杆2做a渐大的加速运动a1≠a2
a1、a2恒定I 恒定杆1做a渐大的加速运动杆2做a渐小的加速运动a1=a2Δv 恒定I 恒定有外力等距式
2.感应电动势与感应电流:感应电动势是形成感应电流的必要条件,有感应电动势不一定存在感应电流(要看电路是否闭合),有感应电流一定存在感应电动势. 2.法拉第电磁感应定律:电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比. 当E、 ?? 、 ?t都取国际单位时,k =1,
所以有: 若线圈有n匝,则相当于n个相同的电动势串联,所以整个线圈中的电动势为.3.法拉第电磁感应定律的应用 ——导体做切割磁感线运动. (1)垂直切割时:如图所示,导体由ab匀速移动到a1b1 ,这一过程中穿过闭合回路的磁通量变化??=BLv?t ,由法拉第电磁感应定律得: (2)切割方向与磁场方向成角时:如图所示,将v分解为垂直B和平行B的两个分量,其中:所以可知:导线切割磁感线时产生的电动势的大小,跟磁感强度B、导线长度L、运动速度v以及运动方向与磁感线方向的夹角的正弦sin?成正比例题1: 长为L的金属棒ab,绕b端在垂直于匀强磁场的平面内以角速度匀速转动,磁感应强度为B,如图所示,求ab两端的电势差.解析: ab两端电势差等于金属棒切割磁感线产生的电动势(因为没有外电路),所以只要求出电动势即可.棒上各处速率不等,不能直接用E=BLv来求,但棒上各点的速度v=? r与半径成正比,因此可用棒的中点速度作为平均切割速度代入公式计算:例题2、如下图所示,半径为r的金属环绕通过某直径的轴OO’以角速度ω作匀速转动,匀强磁场的磁感应强度为B,从金属环面与磁场方向重合时开始计时,则在金属环转过30°角的过程中,环中产生的电动势的平均值是多大?分析:根据金属环在磁场中转动的始末位置穿过环的磁通量Φ1和Φ2以及完成这一变化所用时间△t,就可以求出环中产生的感应电动势 .例题3、如图所示把线框abcd从磁感应强度为的匀强磁场中匀速拉出,速度方向与ab边垂直向右,速度的大小为v,线圈的边长为L,每边的电阻为r,问,线圈在运动过程中,ab两点的电势差为多少?当线框abcd 整个在磁场的时候,穿过线圈的磁通量不变,无感应电流,ab和cd两边切割磁感线,等效电路图如图2所示:
Uab=E=BLv
当cd边离开磁场,ab边切割磁感线,ad,bc,cd边的电阻属于外阻,等效电路图如图3所示:
Uab=E-Ir=BLv-Ir 当线框abcd 整个在磁场的时候:Uab=E=BLv
当cd 边离开磁场的时候:Uab =3BLv/4 电动式发电式阻尼式一、单棒问题运动特点最终特征a逐渐减小的减速运动静止a逐渐减小的加速运动匀速a逐渐减小的加速运动匀速基本模型I=0 (或恒定)I 恒定I=0画等效电路二、含容式单棒问题放电式无外力充电式运动特点最终特征基本模型有外力充电式a逐渐减小的加速运动匀速运动I=0a逐渐减小的减速运动匀速运动I=0匀加速运动匀加速运动I 恒定三、无外力双棒问题运动特点最终特征基本模型杆1做a渐小的加速运动杆2做a渐小的减速运动v1=v2I=0无外力等距式杆1做a渐小的减速运动杆2做a渐小的加速运动无外力 不等距式a=0I=0L1v1=L2v2四、有外力双棒问题运动特点最终特征基本模型有外力 不等距式杆1做a渐小的加速运动杆2做a渐大的加速运动a1≠a2
a1、a2恒定I 恒定杆1做a渐大的加速运动杆2做a渐小的加速运动a1=a2Δv 恒定I 恒定有外力等距式
同课章节目录
- 第一章 电磁感应
- 第01节 电磁感应现象
- 第02节 研究产生感应电流的条件
- 第03节 探究感应电流的方向
- 第04节 法拉第电磁感应定律
- 第05节 法拉第电磁感应定律应用(一)
- 第06节 法拉第电磁感应定律应用(二)
- 第07节 自感现象及其应用
- 第08节 涡流现象及其应用
- 第二章 交变电流
- 第01节 认识变交电流
- 第02节 交变电流的描述
- 第03节 表征交变电流的物理量
- 第04节 电感器对交变电流的作用
- 第05节 电容器对交变电流的作用
- 第06节 变压器
- 第07节 远距离输电
- 第三章 传感器
- 第01节 认识传感器
- 第02节 探究传感器的原理
- 第03节 传感器的应用
- 第04节 用传感器制作自控装置
- 第05节 用传感器测磁感应强度
