必修2 第二章 第一节 点线面基本关系 课时练习
文档属性
| 名称 | 必修2 第二章 第一节 点线面基本关系 课时练习 |
|
|
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-19 00:00:00 | ||
图片预览



文档简介
点、线、面的位置关系
一、单选题
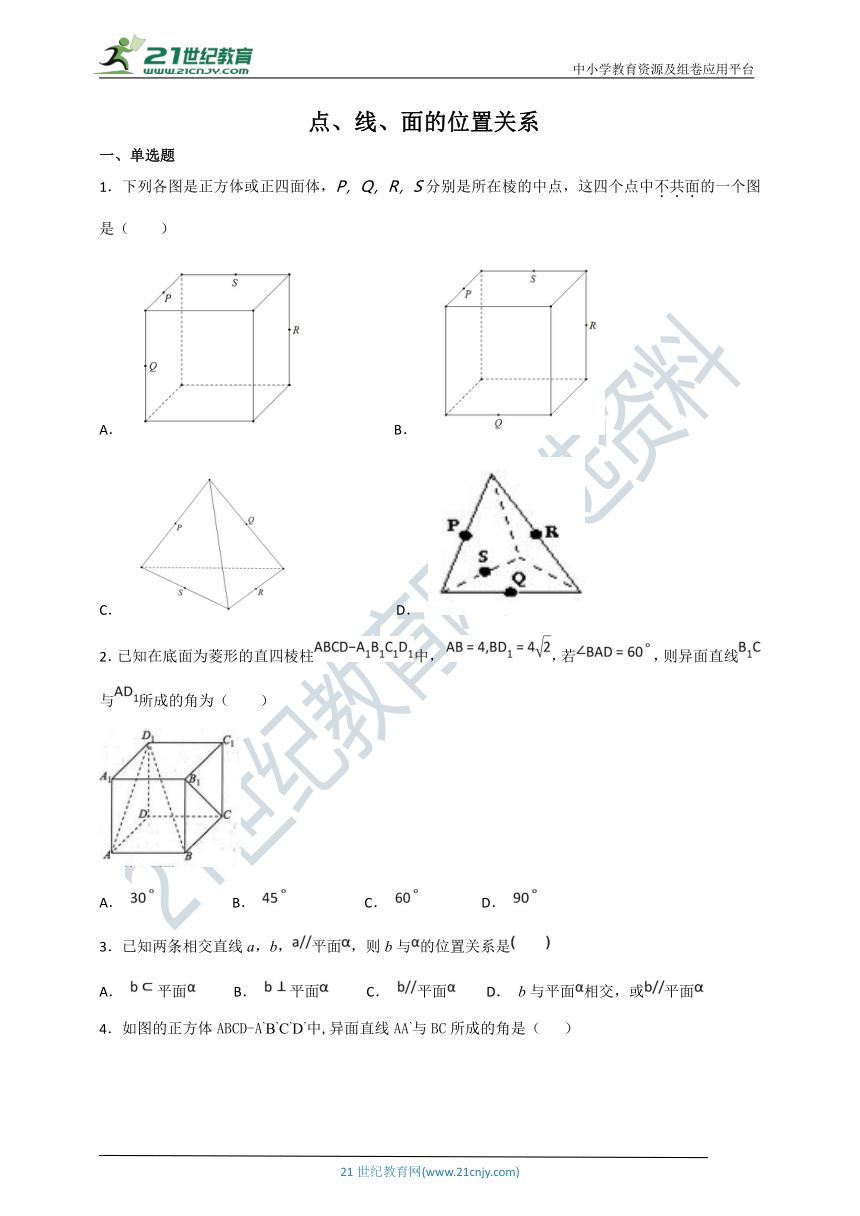
1.下列各图是正方体或正四面体,P,Q,R,S分别是所在棱的中点,这四个点中不共面的一个图是( )
A. B.
C. D.
2.已知在底面为菱形的直四棱柱中, ,若,则异面直线与所成的角为( )
A. B. C. D.
3.已知两条相交直线a,b,平面,则b与的位置关系是
A. 平面 B. 平面 C. 平面 D. b与平面相交,或平面
4.如图的正方体ABCD-A’B’C’D’中,异面直线AA’与BC所成的角是( )
A. 300 B. 450 C. 600 D. 900
5.下列命题错误的是( )
A. 若直线平行于平面,则平面内存在直线与平行
B. 若直线平行于平面,则平面内存在直线与异面
C. 若直线平行于平面,则平面内存在直线与垂直
D. 若直线平行于平面,则平面内存在直线与相交
6.下面四个条件中,能确定一个平面的条件是( ).
A. 空间中任意三点 B. 空间中两条直线 C. 一条直线和一个点 D. 两条平行直线
7.下列命题正确的个数为
①梯形一定是平面图形;
②若两条直线和第三条直线所成的角相等,则这两条直线平行;
③两两相交的三条直线最多可以确定三个平面;
如果两个平面有三个公共点,则这两个平面重合.
A. 0 B. 1 C. 2 D. 3
8.下列命题中,错误的命题是( )
A. 平行于同一平面的两个平面平面
B. 平行于同一直线的两个平面平行
C. 一条直线与两个平行平面中的一个相交,那么这条直线必和另一个平面相交
D. 一条直线与两个平行平面所成的角相等
9.已知是异面直线,直线平行于直线,那么与( )
A. 一定是异面直线 B. 一定是相交直线
C. 不可能是平行直线 D. 不可能是相交直线
10.在下列命题中,不是公理的是( )
A. 平行于同一条直线的两条直线互相平行
B. 如果一条直线上的两点在一个平面内,那么这条直线在此平面内
C. 空间中,如果两个角的两边分别对应平行,那么这两角相等或互补
D. 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
二、填空题
11.以下命题:①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;②没有公共点的直线是异面直线;③经过一条直线及这条直线外一点有且只有一个平面;④有两个面互相平行,其余各面都是梯形的多面体是棱台;⑤空间中,如果两个角的两边分别对应平行,那么这两个角相等或互补,其中正确命题有___________.
12.一个正方体纸盒展开后如图所示,在原正方体纸盒中有如下结论
①AB⊥EF;
②AB与CM所成的角为60°;
③EF与MN是异面直线;
④MN∥CD.
以上四个命题中,正确命题的序号是 _________
13.下列命题不正确的是________.
①如果两条直线都和第三条直线垂直,那么这两条直线平行;
②如果两条直线和第三条直线所成的角相等,那么这两条直线平行;
③两条异面直线所成的角为锐角或直角;
④直线a与b异面,b与c也异面,则直线a与c必异面.
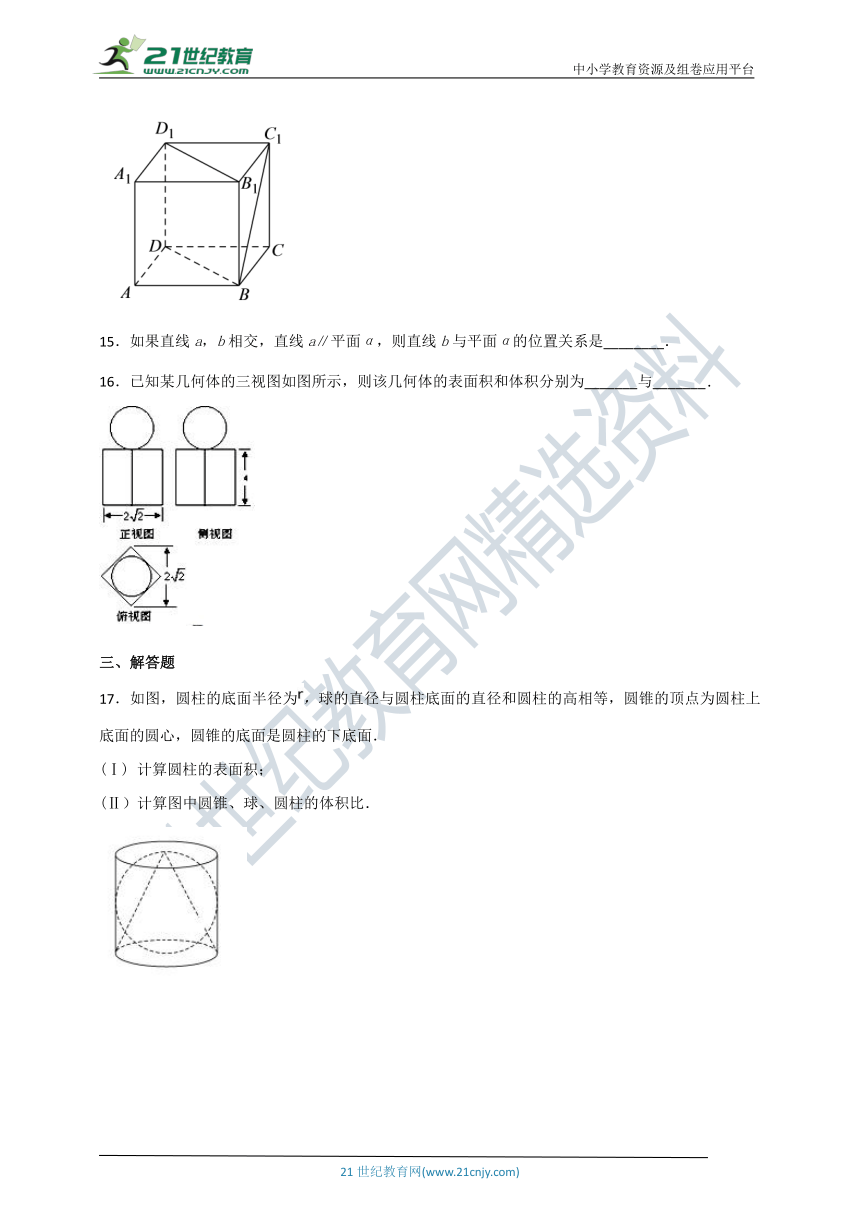
14.如图,正方体中,直线和所成角的大小为___________,直线和平面所成角的大小为___________.
15.如果直线a,b相交,直线a∥平面α,则直线b与平面α的位置关系是________.
16.已知某几何体的三视图如图所示,则该几何体的表面积和体积分别为_______与_______.
三、解答题
17.如图,圆柱的底面半径为,球的直径与圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面.
(Ⅰ) 计算圆柱的表面积;
(Ⅱ)计算图中圆锥、球、圆柱的体积比.
18.如图,一个圆锥的底面半径为1,高为3,在圆锥中有一个半径为x的内接圆柱.
(1)试用x表示圆柱的高;
(2)当x为何值时,圆柱的侧面积最大,最大侧面积是多少
参考答案
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
D
D
D
D
C
B
C
C
11.③⑤ 12.①③ 13.①②④ 14. 15.相交或平行 16.
17.(Ⅰ) ;(Ⅱ).
【详解】
(Ⅰ)已知圆柱的底面半径为,则圆柱和圆锥的高为,圆锥和球的底面半径为,则圆柱的表面积为;
(Ⅱ)由(Ⅰ)知,
,
18.(1)h=3-3x(2)当 时,它的侧面积最大为π
【解析】
【分析】
(1)利用圆锥轴截面的特征可得圆柱的高h可表示为h=3-3x.
(2)由题意可得S圆柱侧=6π(x-x2),利用二次函数的性质可得当圆柱的底面半径为时,它的侧面积最大为π.
【详解】
(1)设所求的圆柱的底面半径为x,它的轴截面如图,
BO=1,PO=3,圆柱的高为h,
由图,得=,即h=3-3x.
(2)∵S圆柱侧=2πhx=2π(3-3x)x=6π(x-x2),
当x=时,圆柱的侧面积取得最大值为π.
∴当圆柱的底面半径为时,它的侧面积最大为π.
一、单选题
1.下列各图是正方体或正四面体,P,Q,R,S分别是所在棱的中点,这四个点中不共面的一个图是( )
A. B.
C. D.
2.已知在底面为菱形的直四棱柱中, ,若,则异面直线与所成的角为( )
A. B. C. D.
3.已知两条相交直线a,b,平面,则b与的位置关系是
A. 平面 B. 平面 C. 平面 D. b与平面相交,或平面
4.如图的正方体ABCD-A’B’C’D’中,异面直线AA’与BC所成的角是( )
A. 300 B. 450 C. 600 D. 900
5.下列命题错误的是( )
A. 若直线平行于平面,则平面内存在直线与平行
B. 若直线平行于平面,则平面内存在直线与异面
C. 若直线平行于平面,则平面内存在直线与垂直
D. 若直线平行于平面,则平面内存在直线与相交
6.下面四个条件中,能确定一个平面的条件是( ).
A. 空间中任意三点 B. 空间中两条直线 C. 一条直线和一个点 D. 两条平行直线
7.下列命题正确的个数为
①梯形一定是平面图形;
②若两条直线和第三条直线所成的角相等,则这两条直线平行;
③两两相交的三条直线最多可以确定三个平面;
如果两个平面有三个公共点,则这两个平面重合.
A. 0 B. 1 C. 2 D. 3
8.下列命题中,错误的命题是( )
A. 平行于同一平面的两个平面平面
B. 平行于同一直线的两个平面平行
C. 一条直线与两个平行平面中的一个相交,那么这条直线必和另一个平面相交
D. 一条直线与两个平行平面所成的角相等
9.已知是异面直线,直线平行于直线,那么与( )
A. 一定是异面直线 B. 一定是相交直线
C. 不可能是平行直线 D. 不可能是相交直线
10.在下列命题中,不是公理的是( )
A. 平行于同一条直线的两条直线互相平行
B. 如果一条直线上的两点在一个平面内,那么这条直线在此平面内
C. 空间中,如果两个角的两边分别对应平行,那么这两角相等或互补
D. 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
二、填空题
11.以下命题:①以直角三角形的一边为轴旋转一周所得的旋转体是圆锥;②没有公共点的直线是异面直线;③经过一条直线及这条直线外一点有且只有一个平面;④有两个面互相平行,其余各面都是梯形的多面体是棱台;⑤空间中,如果两个角的两边分别对应平行,那么这两个角相等或互补,其中正确命题有___________.
12.一个正方体纸盒展开后如图所示,在原正方体纸盒中有如下结论
①AB⊥EF;
②AB与CM所成的角为60°;
③EF与MN是异面直线;
④MN∥CD.
以上四个命题中,正确命题的序号是 _________
13.下列命题不正确的是________.
①如果两条直线都和第三条直线垂直,那么这两条直线平行;
②如果两条直线和第三条直线所成的角相等,那么这两条直线平行;
③两条异面直线所成的角为锐角或直角;
④直线a与b异面,b与c也异面,则直线a与c必异面.
14.如图,正方体中,直线和所成角的大小为___________,直线和平面所成角的大小为___________.
15.如果直线a,b相交,直线a∥平面α,则直线b与平面α的位置关系是________.
16.已知某几何体的三视图如图所示,则该几何体的表面积和体积分别为_______与_______.
三、解答题
17.如图,圆柱的底面半径为,球的直径与圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面.
(Ⅰ) 计算圆柱的表面积;
(Ⅱ)计算图中圆锥、球、圆柱的体积比.
18.如图,一个圆锥的底面半径为1,高为3,在圆锥中有一个半径为x的内接圆柱.
(1)试用x表示圆柱的高;
(2)当x为何值时,圆柱的侧面积最大,最大侧面积是多少
参考答案
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
D
D
D
D
C
B
C
C
11.③⑤ 12.①③ 13.①②④ 14. 15.相交或平行 16.
17.(Ⅰ) ;(Ⅱ).
【详解】
(Ⅰ)已知圆柱的底面半径为,则圆柱和圆锥的高为,圆锥和球的底面半径为,则圆柱的表面积为;
(Ⅱ)由(Ⅰ)知,
,
18.(1)h=3-3x(2)当 时,它的侧面积最大为π
【解析】
【分析】
(1)利用圆锥轴截面的特征可得圆柱的高h可表示为h=3-3x.
(2)由题意可得S圆柱侧=6π(x-x2),利用二次函数的性质可得当圆柱的底面半径为时,它的侧面积最大为π.
【详解】
(1)设所求的圆柱的底面半径为x,它的轴截面如图,
BO=1,PO=3,圆柱的高为h,
由图,得=,即h=3-3x.
(2)∵S圆柱侧=2πhx=2π(3-3x)x=6π(x-x2),
当x=时,圆柱的侧面积取得最大值为π.
∴当圆柱的底面半径为时,它的侧面积最大为π.
