人教版数学八年级上 册 11.2.2三角形的外角 课件(共23张ppt)
文档属性
| 名称 | 人教版数学八年级上 册 11.2.2三角形的外角 课件(共23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 448.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-21 10:07:31 | ||
图片预览




文档简介
课件23张PPT。11.2.2 三角形的外角
1、理解三角形的外角;
2、掌握三角形外角的性质,能利用三角形外角的性质解决问题。 2、在ABC中,
(1)∠C=90°,∠A=30 ° ,则∠B= ;
(2)∠A=50 ° ,∠B=∠C,则∠B= .1、三角形三个内角的和等于多少度?3、在△ABC中,
∠A:∠B:∠C=2:3:4. 则∠A= ,
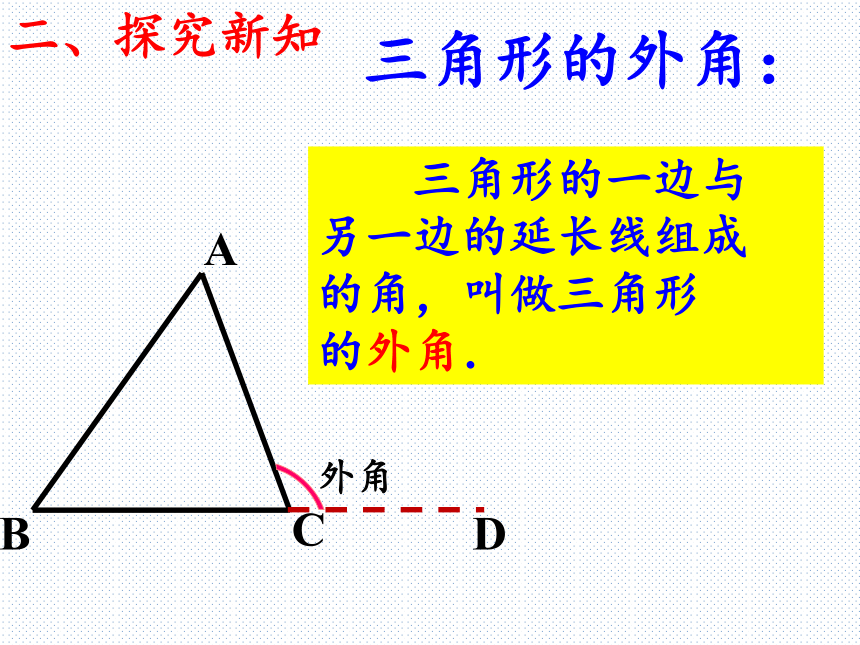
∠B= ,∠C= . 40°60°80°65°60°怎么验证呢?一、复习引入D三角形的外角: 三角形的一边与
另一边的延长线组成
的角,叫做三角形
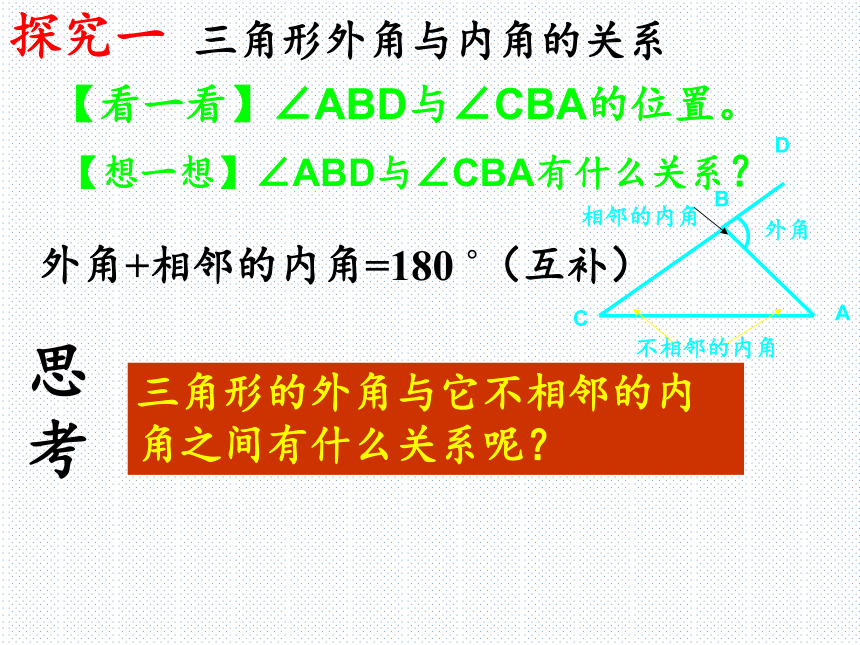
的外角.外角二、探究新知外角三角形外角与内角的关系外角+相邻的内角=180 ?(互补)相邻的内角不相邻的内角思考三角形的外角与它不相邻的内角之间有什么关系呢?ABCD【看一看】∠ABD与∠CBA的位置。【想一想】∠ABD与∠CBA有什么关系?
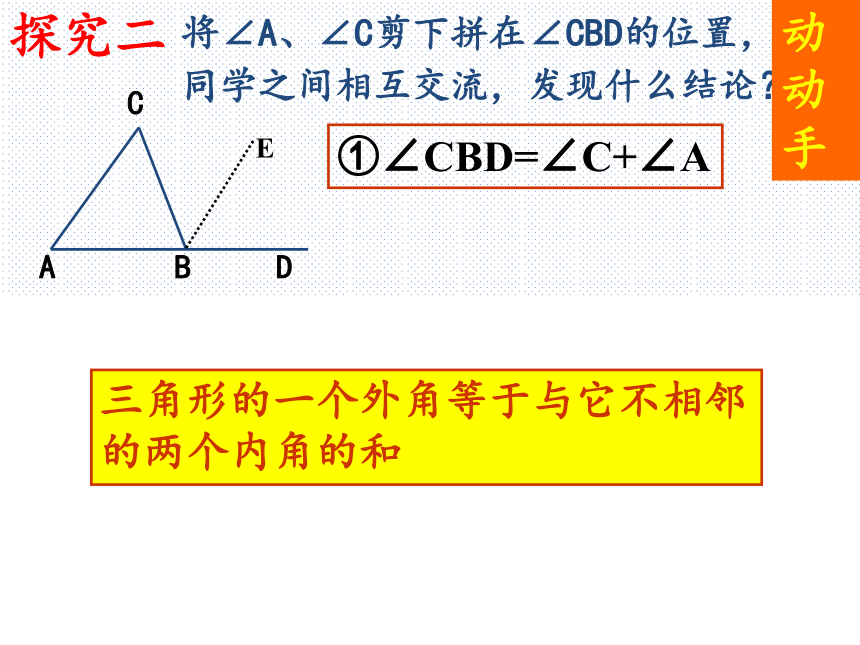
探究一探究二①∠CBD=∠C+∠A将∠A、∠C剪下拼在∠CBD的位置,
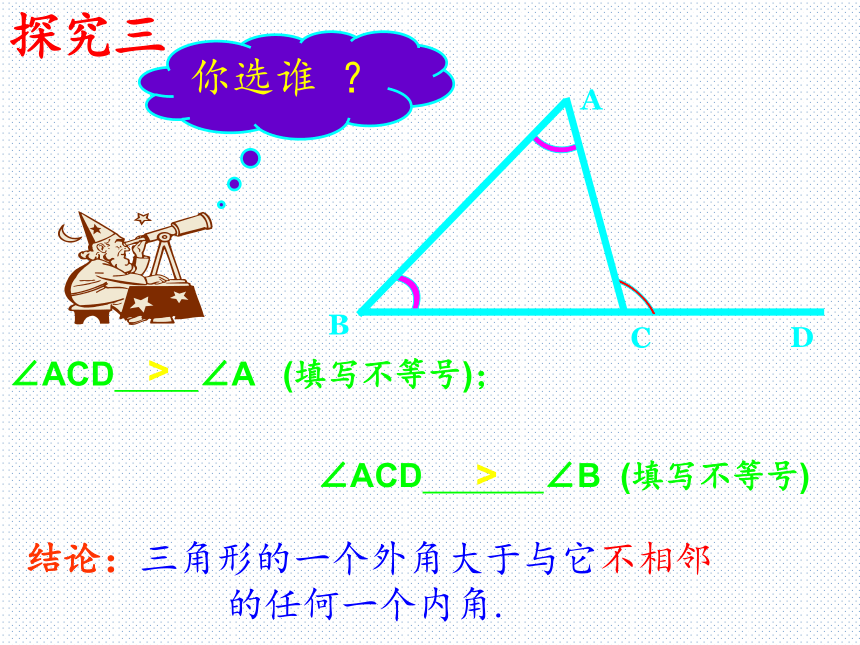
同学之间相互交流,发现什么结论?动动手E∵ ∠ABC + ∠CBD= 180 °又∵ ∠ABC+ ∠C+ ∠A= 180 °∴ ∠CBD= ∠C+ ∠A证明(一)证明(二):过B点作 BE∥AC∴ ∠EBD = ∠A ∠CBE = ∠C ∴ ∠CBD = ∠CBE+ ∠EBD= ∠C+ ∠A三角形的一个外角等于与它不相邻的两个内角的和三角形的一个外角等于与它不相邻的两个内角的和三角形的一个外角与它相邻的内角互补 ∠ACD ∠A (填写不等号);∠ACD ∠B (填写不等号)结论:三角形的一个外角大于与它不相邻的任何一个内角.D>>探究三三角形的外角与内角的关系:
1、三角形的一个外角与它相邻的内角 ;
2、三角形的一个外角 与它不相邻的
两个内角的和;
3、三角形的一个外角 任何一个与它
不相邻的内角。等于大于互补归纳总结1、快速抢答,看谁答得又快又准。
∠1=_________+__________
∠2=_________+__________
∠2________∠3,
∠2________∠4
341∠CAD∠C∠3∠4>>三、课堂练习2、求下列各图中∠1的度数。90°95°85°3、把图中∠1、 ∠2、 ∠3按由大到小的顺序排列∠1>∠2>∠3找出△ABC的所有外角,共有几个外角?共有6个外角:FIEGDH∠1, ∠2, ∠3,
∠4, ∠5, ∠6。123645∠1+∠2 +∠3就是△ABC的外角和 四、探究三角形的外角和 ∠1+∠2 +∠3 = ?
从哪些途径探究这个结果?议一议321ABC三角形的外角和等于360°方法1方法2go∠2+ ∠ABC=180°∠3+ ∠ACB=180°三个式子相加得到∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°而∠BAC+ ∠ABC+∠ACB=180°∠1+ ∠2+ ∠3=360°解:过A作AD平行于BC∠3= ∠4BC123A∠2= ∠BAD所以, ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠BAD=360°∠2+ ∠ 3= ∠ 4+∠BAD1.三角形的外角和是指三角形所有外角和
2.三角形的外角和等于它内角和的2倍。
3.三角形的一个外角等于两个内角的和。
4、三角形的一个外角等于与它不相邻的两个内角的和。
5.三角形的一个外角大于任何一个内角。
6.三角形的一个外角大于任何一个不相邻的内角练习巩固五、运用新知例1:如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.(1)解:∵∠B+∠BAD=∠ADC
∴∠B+∠BAD=80°
又∵∠B=∠BAD
∴∠B=1/2∠ADC=40°例1:如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.(2)解法1:∵∠DAC+∠BAD=∠BAC
∴∠DAC=∠BAC-∠BAD=70°-40=30°
又∵∠C=180°-∠ADC-∠DAC
∴∠C=180°-80°-30°=70°五、运用新知例1:如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.(2)解法2:∵∠B+∠BAC+∠C=180°
∴∠C=180°-∠B-∠BAC
=180°-40°-70°=70°五、运用新知3.三角形的一个外角大于任何一个与它不相邻的内角.2.三角形的一个外角等于与它不相邻的两个内角的和;1.三角形的一个外角与它相邻的内角互补;三角形的外角与内角的关系:六、课堂小结天生我才2.(1)如图(1),BD、CD都是△ABC两个外角的∠CBE、∠BCF的平分线,试探索∠BDC和∠A之间的数量关系.
(2)如图(2)所示,BD是△ABC的角平分线,CD是△ABC的外角平分线,它们相交于点D,试探索∠BDC和∠A之间的数量关系.再见!
1、理解三角形的外角;
2、掌握三角形外角的性质,能利用三角形外角的性质解决问题。 2、在ABC中,
(1)∠C=90°,∠A=30 ° ,则∠B= ;
(2)∠A=50 ° ,∠B=∠C,则∠B= .1、三角形三个内角的和等于多少度?3、在△ABC中,
∠A:∠B:∠C=2:3:4. 则∠A= ,
∠B= ,∠C= . 40°60°80°65°60°怎么验证呢?一、复习引入D三角形的外角: 三角形的一边与
另一边的延长线组成
的角,叫做三角形
的外角.外角二、探究新知外角三角形外角与内角的关系外角+相邻的内角=180 ?(互补)相邻的内角不相邻的内角思考三角形的外角与它不相邻的内角之间有什么关系呢?ABCD【看一看】∠ABD与∠CBA的位置。【想一想】∠ABD与∠CBA有什么关系?
探究一探究二①∠CBD=∠C+∠A将∠A、∠C剪下拼在∠CBD的位置,
同学之间相互交流,发现什么结论?动动手E∵ ∠ABC + ∠CBD= 180 °又∵ ∠ABC+ ∠C+ ∠A= 180 °∴ ∠CBD= ∠C+ ∠A证明(一)证明(二):过B点作 BE∥AC∴ ∠EBD = ∠A ∠CBE = ∠C ∴ ∠CBD = ∠CBE+ ∠EBD= ∠C+ ∠A三角形的一个外角等于与它不相邻的两个内角的和三角形的一个外角等于与它不相邻的两个内角的和三角形的一个外角与它相邻的内角互补 ∠ACD ∠A (填写不等号);∠ACD ∠B (填写不等号)结论:三角形的一个外角大于与它不相邻的任何一个内角.D>>探究三三角形的外角与内角的关系:
1、三角形的一个外角与它相邻的内角 ;
2、三角形的一个外角 与它不相邻的
两个内角的和;
3、三角形的一个外角 任何一个与它
不相邻的内角。等于大于互补归纳总结1、快速抢答,看谁答得又快又准。
∠1=_________+__________
∠2=_________+__________
∠2________∠3,
∠2________∠4
341∠CAD∠C∠3∠4>>三、课堂练习2、求下列各图中∠1的度数。90°95°85°3、把图中∠1、 ∠2、 ∠3按由大到小的顺序排列∠1>∠2>∠3找出△ABC的所有外角,共有几个外角?共有6个外角:FIEGDH∠1, ∠2, ∠3,
∠4, ∠5, ∠6。123645∠1+∠2 +∠3就是△ABC的外角和 四、探究三角形的外角和 ∠1+∠2 +∠3 = ?
从哪些途径探究这个结果?议一议321ABC三角形的外角和等于360°方法1方法2go∠2+ ∠ABC=180°∠3+ ∠ACB=180°三个式子相加得到∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°而∠BAC+ ∠ABC+∠ACB=180°∠1+ ∠2+ ∠3=360°解:过A作AD平行于BC∠3= ∠4BC123A∠2= ∠BAD所以, ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠BAD=360°∠2+ ∠ 3= ∠ 4+∠BAD1.三角形的外角和是指三角形所有外角和
2.三角形的外角和等于它内角和的2倍。
3.三角形的一个外角等于两个内角的和。
4、三角形的一个外角等于与它不相邻的两个内角的和。
5.三角形的一个外角大于任何一个内角。
6.三角形的一个外角大于任何一个不相邻的内角练习巩固五、运用新知例1:如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.(1)解:∵∠B+∠BAD=∠ADC
∴∠B+∠BAD=80°
又∵∠B=∠BAD
∴∠B=1/2∠ADC=40°例1:如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.(2)解法1:∵∠DAC+∠BAD=∠BAC
∴∠DAC=∠BAC-∠BAD=70°-40=30°
又∵∠C=180°-∠ADC-∠DAC
∴∠C=180°-80°-30°=70°五、运用新知例1:如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.(2)解法2:∵∠B+∠BAC+∠C=180°
∴∠C=180°-∠B-∠BAC
=180°-40°-70°=70°五、运用新知3.三角形的一个外角大于任何一个与它不相邻的内角.2.三角形的一个外角等于与它不相邻的两个内角的和;1.三角形的一个外角与它相邻的内角互补;三角形的外角与内角的关系:六、课堂小结天生我才2.(1)如图(1),BD、CD都是△ABC两个外角的∠CBE、∠BCF的平分线,试探索∠BDC和∠A之间的数量关系.
(2)如图(2)所示,BD是△ABC的角平分线,CD是△ABC的外角平分线,它们相交于点D,试探索∠BDC和∠A之间的数量关系.再见!
