2.1.5__第2课时__点到直线的距离公式
文档属性
| 名称 | 2.1.5__第2课时__点到直线的距离公式 |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-21 07:49:18 | ||
图片预览




文档简介
第2课时 点到直线的距离公式
仓库
铁路
点到直线的距离
l
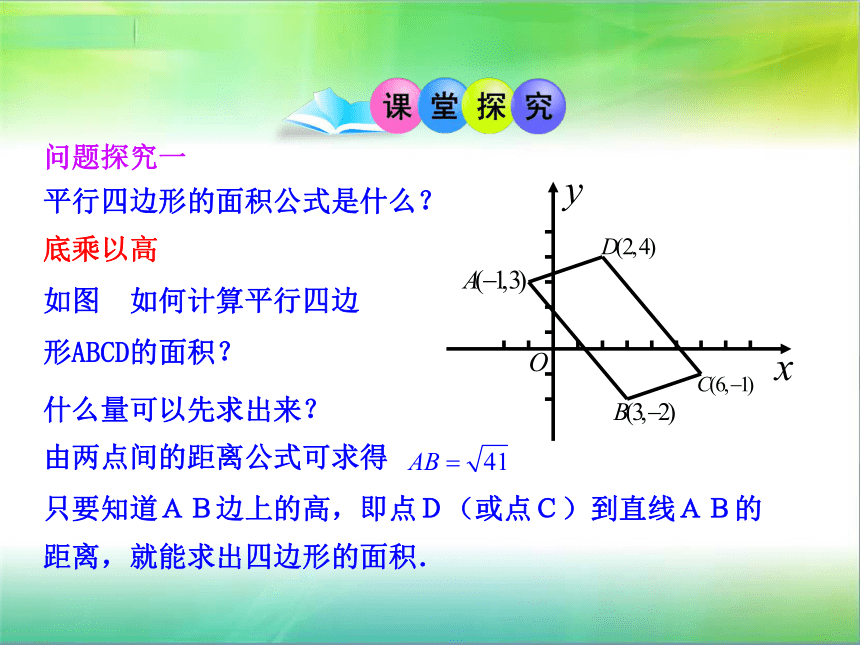
问题探究一
平行四边形的面积公式是什么?
如图 如何计算平行四边形ABCD的面积?
什么量可以先求出来?
底乘以高
由两点间的距离公式可求得
只要知道AB边上的高,即点D(或点C)到直线AB的距离,就能求出四边形的面积.
如何计算点D(2,4)到直线AB:5x+4y-7=0的距离呢?
过点D作DE⊥AB,垂足为E,则点D到直线AB的距离就是线段DE的长.
方法一:通过求点E的坐标,用两点间的距离公式求DE.
1.由DE⊥AB,可知DE所在直线的斜率为:
2.求出DE的方程即4x-5y+12=0.
3.由AB和DE所在直线的方程
4.用两点间的距离公式,求出点D到AB的距离
方法一的不足:运算量较大.
下面我们通过构造三角形,利用面积关系求出点D到AB的距离.
一般地,对于直线
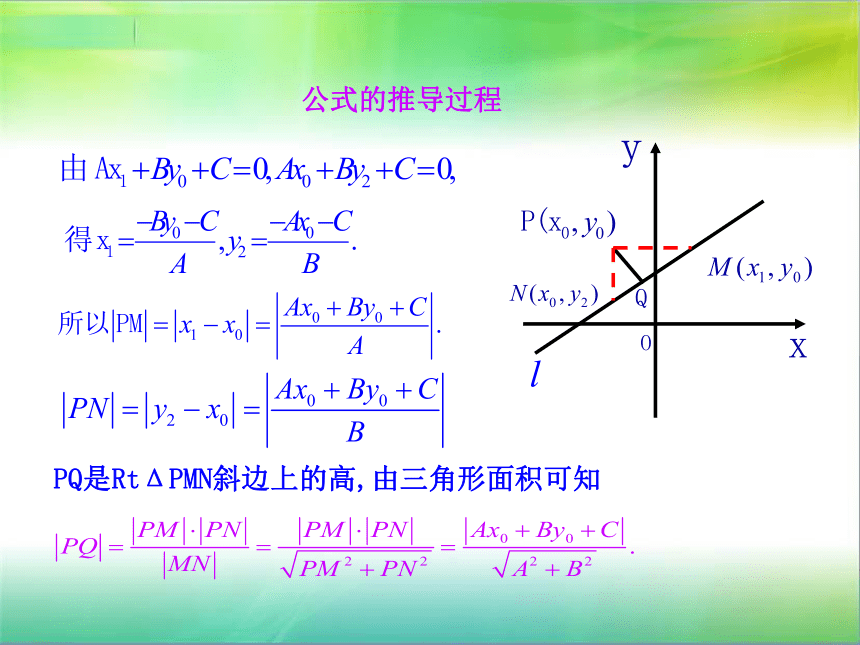
公式的推导过程
PQ是RtΔPMN斜边上的高,由三角形面积可知
公式的推导过程
由此我们得到,
的距离
点到直线的距离公式
点 到直线
点到直线的距离公式
注: ?在使用该公式 前,须将直线方程化为一般式.
? A=0或B=0,此公式也成立,
但当A=0或B=0时一般不用此
公式计算距离.
例1:求点P(-1,2)到直线①2x+y-10=0; ②3x=2的距离。
解: ①根据点到直线的距离公式,得
②如图,直线3x=2平行于y轴,
用公式验证,结果怎样?
求下列点到直线的距离:
(1)(0,0),3x-2y+4=0 (2)(2,-3),x=y
练习
例2: 用解析法证明:等腰三角形底边延长线上一点到两腰的距离之差等于一腰上的高.
解:在△ABC中,AB=AC,P为BC延长线上一点,PD⊥AB于D,PE ⊥ AC于E,CF ⊥AB于F.以BC所在直线为x轴,以BC的中垂线为y轴,建立直角坐标系.
设A(0,b),B(-a,0),C(a,0)(a>0,b>0),则直线AB方
程为bx-ay+ab=0,直线AC方程为bx+ay-ab=0,取P(x0,0),
使x0>a,
则点P到直线AB,AC的距离分别为
例2: 求平行线2x-7y+8=0与2x-7y-6=0的距离。
两平行线间的距离处处相等
在l2上任取一点,例如P(3,0)
P到l1的距离等于l1与l2的距离
?直线到直线的距离转化为点到直线的距离
任意两条平行直线都可以写成如下形式:
P
Q
思考:任意两条平行线的距离是多少呢?
注:用两平行线间距离公式须将方程中x、y的系数化为
对应相同的形式。
(两平行线间
的距离公式)
求下列两条平行直线的距离:
(1) 3x-2y-1=0,3x-2y+6=0
(2) x+2y=0,2x+4y-7=0
练习
反馈练习:
( )
( )
D
B
( )
( )
D
A
注意用该公式时应先将直线方程化为一般式;
注意用该公式时应先将两平行线的x,y的系数整理
为对应相等的形式。
不是拥有幸福的人才幸福,而是知道幸福的人才幸福。幸福不在于享受了多少,而在于感受了多少。
仓库
铁路
点到直线的距离
l
问题探究一
平行四边形的面积公式是什么?
如图 如何计算平行四边形ABCD的面积?
什么量可以先求出来?
底乘以高
由两点间的距离公式可求得
只要知道AB边上的高,即点D(或点C)到直线AB的距离,就能求出四边形的面积.
如何计算点D(2,4)到直线AB:5x+4y-7=0的距离呢?
过点D作DE⊥AB,垂足为E,则点D到直线AB的距离就是线段DE的长.
方法一:通过求点E的坐标,用两点间的距离公式求DE.
1.由DE⊥AB,可知DE所在直线的斜率为:
2.求出DE的方程即4x-5y+12=0.
3.由AB和DE所在直线的方程
4.用两点间的距离公式,求出点D到AB的距离
方法一的不足:运算量较大.
下面我们通过构造三角形,利用面积关系求出点D到AB的距离.
一般地,对于直线
公式的推导过程
PQ是RtΔPMN斜边上的高,由三角形面积可知
公式的推导过程
由此我们得到,
的距离
点到直线的距离公式
点 到直线
点到直线的距离公式
注: ?在使用该公式 前,须将直线方程化为一般式.
? A=0或B=0,此公式也成立,
但当A=0或B=0时一般不用此
公式计算距离.
例1:求点P(-1,2)到直线①2x+y-10=0; ②3x=2的距离。
解: ①根据点到直线的距离公式,得
②如图,直线3x=2平行于y轴,
用公式验证,结果怎样?
求下列点到直线的距离:
(1)(0,0),3x-2y+4=0 (2)(2,-3),x=y
练习
例2: 用解析法证明:等腰三角形底边延长线上一点到两腰的距离之差等于一腰上的高.
解:在△ABC中,AB=AC,P为BC延长线上一点,PD⊥AB于D,PE ⊥ AC于E,CF ⊥AB于F.以BC所在直线为x轴,以BC的中垂线为y轴,建立直角坐标系.
设A(0,b),B(-a,0),C(a,0)(a>0,b>0),则直线AB方
程为bx-ay+ab=0,直线AC方程为bx+ay-ab=0,取P(x0,0),
使x0>a,
则点P到直线AB,AC的距离分别为
例2: 求平行线2x-7y+8=0与2x-7y-6=0的距离。
两平行线间的距离处处相等
在l2上任取一点,例如P(3,0)
P到l1的距离等于l1与l2的距离
?直线到直线的距离转化为点到直线的距离
任意两条平行直线都可以写成如下形式:
P
Q
思考:任意两条平行线的距离是多少呢?
注:用两平行线间距离公式须将方程中x、y的系数化为
对应相同的形式。
(两平行线间
的距离公式)
求下列两条平行直线的距离:
(1) 3x-2y-1=0,3x-2y+6=0
(2) x+2y=0,2x+4y-7=0
练习
反馈练习:
( )
( )
D
B
( )
( )
D
A
注意用该公式时应先将直线方程化为一般式;
注意用该公式时应先将两平行线的x,y的系数整理
为对应相等的形式。
不是拥有幸福的人才幸福,而是知道幸福的人才幸福。幸福不在于享受了多少,而在于感受了多少。
