2018_2019学年九年级数学上册第一章特殊平行四边形3正方形的性质与判定 习题巩固(含解析)
文档属性
| 名称 | 2018_2019学年九年级数学上册第一章特殊平行四边形3正方形的性质与判定 习题巩固(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 95.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-21 00:00:00 | ||
图片预览

文档简介
正方形
【巩固练习】
一.选择题
1. 如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
2. 正方形具有而菱形不一定具有的性质是( )
A. 四条边相等 B. 对角线互相垂直平分
C. 对角线平分一组对角 D. 对角线相等
3. 如图,正方形ABCD的边长为4,则图中阴影部分的面积为( ).
6 B. 8 C. 16 D. 不能确定
4. 顺次连结对角线互相垂直的四边形各边的中点,所得的四边形是( )
A. 矩形 B. 菱形 C. 正方形 D. 梯形
5. 如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )
A. B. C. D.
如图,正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰三角形有( )
A.4个 B.6个 C.8个 D.10个
二.填空题
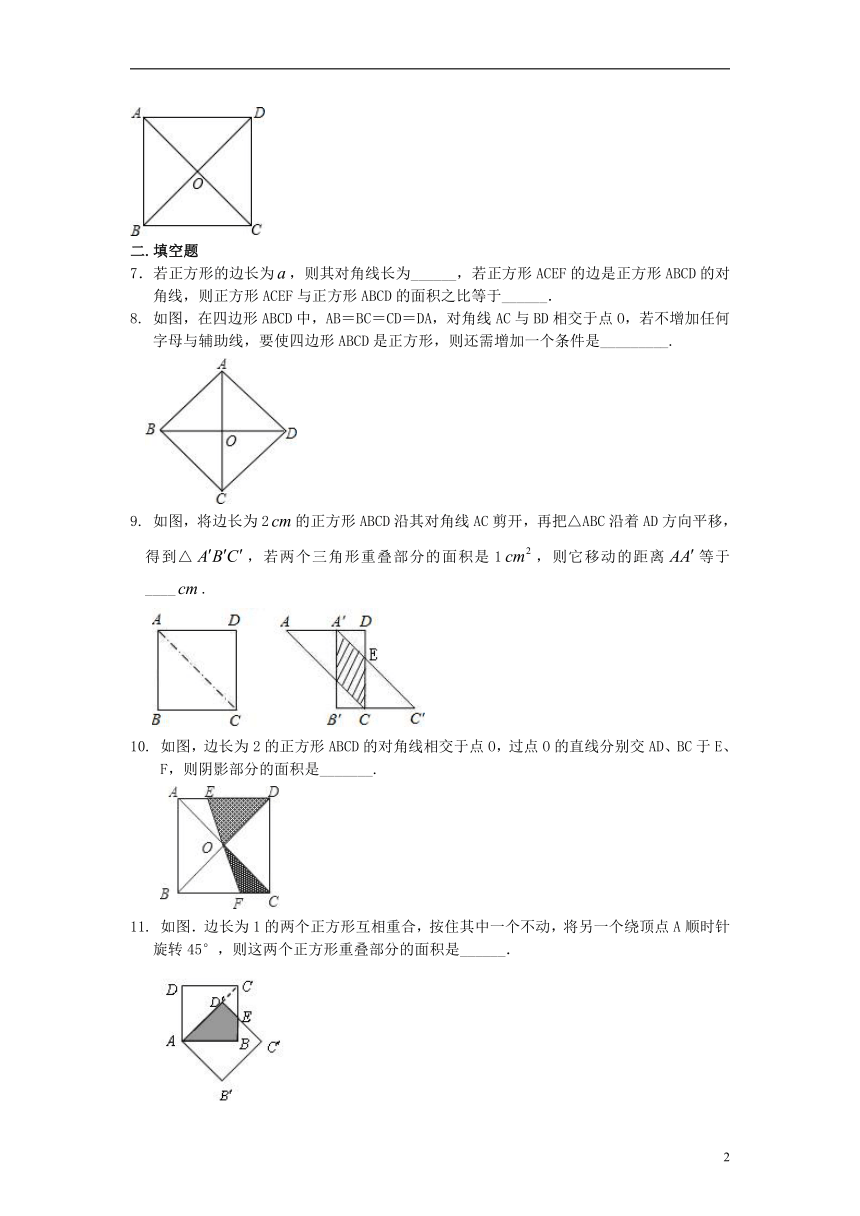
7.若正方形的边长为,则其对角线长为______,若正方形ACEF的边是正方形ABCD的对角线,则正方形ACEF与正方形ABCD的面积之比等于______.
8. 如图,在四边形ABCD中,AB=BC=CD=DA,对角线AC与BD相交于点O,若不增加任何字母与辅助线,要使四边形ABCD是正方形,则还需增加一个条件是_________.
9. 如图,将边长为2的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△,若两个三角形重叠部分的面积是1,则它移动的距离等于____.
10. 如图,边长为2的正方形ABCD的对角线相交于点O,过点O的直线分别交AD、BC于E、F,则阴影部分的面积是_______.
11. 如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是______.
如图,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为 .
三.解答题
13.如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF.
14.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E;PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,正确的有几个?.
15.如图,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后,得到正方形EFCG,EF交AD于H,求DH的长.
【答案与解析】
一.选择题
1.【答案】C.
2.【答案】D;
【解析】正方形的性质:正方形的四条边相等,四个角都是直角,对角线互相垂直平分且相等,并且每一条对角线平分一组对角;
菱形的性质:菱形的四条边相等,对角线互相垂直平分,并且每一条对角线平分一组对角;
因此正方形具有而菱形不一定具有的性质是:对角线相等;故选:D.
3.【答案】B;
【解析】阴影部分面积为正方形面积的一半.
4.【答案】A;
5.【答案】D;
【解析】利用勾股定理求出CM=,即ME的长,有DM=DE,所以可以求出DE=,进而得到DG的长.
6.【答案】C;
二.填空题
7.【答案】,2∶1 ;
【解析】正方形ACEF与正方形ABCD的边长之比为.
8.【答案】AC=BD或AB⊥BC;
【解析】∵在四边形ABCD中,AB=BC=CD=DA∴四边形ABCD是菱形∴要使四边形ABCD是正方形,则还需增加一个条件是AC=BD或AB⊥BC.
9.【答案】1;
【解析】移动距离为,重叠部分面积为CE×,所以,得,所以.
10.【答案】1;
【解析】由题可知△DEO≌△BFO,阴影面积就等于三角形BOC面积.
11.【答案】;
【解析】,重叠部分面积为.
12.【答案】5;
三.解答题
13.【解析】
证明:∵ABCD是正方形,
∴AB=BC=CD,∠EBC=∠FCD=90°,
又∵E、F分别是AB、BC的中点,
∴BE=CF,
在△CEB和△DFC中,
BC=CD,,BE=CF
∴△CEB≌△DFC,
∴CE=DF.
14.【解析】
解:①正确,连接PC,可得PC=EF,PC=PA,∴AP=EF;
②正确;延长AP,交EF于点N,则∠EPN=∠BAP=∠PCE=∠PFE,可得AP⊥EF;
③正确;∠PFE=∠PCE=∠BAP;
④错误,PD=PF=CE;
⑤正确,PB2+PD2=2PA2.
所以正确的有4个:①②③⑤.
15.【解析】
解:如图,连接CH,
∵正方形ABCD绕点C按顺时针方向旋转30°,
∴∠BCF=30°,则∠DCF=60°,
在Rt△CDH和Rt△CFH中,
∴Rt△CDH≌Rt△CFH,
∴∠DCH=∠FCH=∠DCF=30°,
在Rt△CDH中,DH=,CH=2,CD=,
∴DH=.
【巩固练习】
一.选择题
1. 如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
2. 正方形具有而菱形不一定具有的性质是( )
A. 四条边相等 B. 对角线互相垂直平分
C. 对角线平分一组对角 D. 对角线相等
3. 如图,正方形ABCD的边长为4,则图中阴影部分的面积为( ).
6 B. 8 C. 16 D. 不能确定
4. 顺次连结对角线互相垂直的四边形各边的中点,所得的四边形是( )
A. 矩形 B. 菱形 C. 正方形 D. 梯形
5. 如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )
A. B. C. D.
如图,正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰三角形有( )
A.4个 B.6个 C.8个 D.10个
二.填空题
7.若正方形的边长为,则其对角线长为______,若正方形ACEF的边是正方形ABCD的对角线,则正方形ACEF与正方形ABCD的面积之比等于______.
8. 如图,在四边形ABCD中,AB=BC=CD=DA,对角线AC与BD相交于点O,若不增加任何字母与辅助线,要使四边形ABCD是正方形,则还需增加一个条件是_________.
9. 如图,将边长为2的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△,若两个三角形重叠部分的面积是1,则它移动的距离等于____.
10. 如图,边长为2的正方形ABCD的对角线相交于点O,过点O的直线分别交AD、BC于E、F,则阴影部分的面积是_______.
11. 如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是______.
如图,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为 .
三.解答题
13.如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF.
14.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E;PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,正确的有几个?.
15.如图,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后,得到正方形EFCG,EF交AD于H,求DH的长.
【答案与解析】
一.选择题
1.【答案】C.
2.【答案】D;
【解析】正方形的性质:正方形的四条边相等,四个角都是直角,对角线互相垂直平分且相等,并且每一条对角线平分一组对角;
菱形的性质:菱形的四条边相等,对角线互相垂直平分,并且每一条对角线平分一组对角;
因此正方形具有而菱形不一定具有的性质是:对角线相等;故选:D.
3.【答案】B;
【解析】阴影部分面积为正方形面积的一半.
4.【答案】A;
5.【答案】D;
【解析】利用勾股定理求出CM=,即ME的长,有DM=DE,所以可以求出DE=,进而得到DG的长.
6.【答案】C;
二.填空题
7.【答案】,2∶1 ;
【解析】正方形ACEF与正方形ABCD的边长之比为.
8.【答案】AC=BD或AB⊥BC;
【解析】∵在四边形ABCD中,AB=BC=CD=DA∴四边形ABCD是菱形∴要使四边形ABCD是正方形,则还需增加一个条件是AC=BD或AB⊥BC.
9.【答案】1;
【解析】移动距离为,重叠部分面积为CE×,所以,得,所以.
10.【答案】1;
【解析】由题可知△DEO≌△BFO,阴影面积就等于三角形BOC面积.
11.【答案】;
【解析】,重叠部分面积为.
12.【答案】5;
三.解答题
13.【解析】
证明:∵ABCD是正方形,
∴AB=BC=CD,∠EBC=∠FCD=90°,
又∵E、F分别是AB、BC的中点,
∴BE=CF,
在△CEB和△DFC中,
BC=CD,,BE=CF
∴△CEB≌△DFC,
∴CE=DF.
14.【解析】
解:①正确,连接PC,可得PC=EF,PC=PA,∴AP=EF;
②正确;延长AP,交EF于点N,则∠EPN=∠BAP=∠PCE=∠PFE,可得AP⊥EF;
③正确;∠PFE=∠PCE=∠BAP;
④错误,PD=PF=CE;
⑤正确,PB2+PD2=2PA2.
所以正确的有4个:①②③⑤.
15.【解析】
解:如图,连接CH,
∵正方形ABCD绕点C按顺时针方向旋转30°,
∴∠BCF=30°,则∠DCF=60°,
在Rt△CDH和Rt△CFH中,
∴Rt△CDH≌Rt△CFH,
∴∠DCH=∠FCH=∠DCF=30°,
在Rt△CDH中,DH=,CH=2,CD=,
∴DH=.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
