第三章 牛顿第二定律的应用(四)第4课时
文档属性
| 名称 | 第三章 牛顿第二定律的应用(四)第4课时 |  | |
| 格式 | rar | ||
| 文件大小 | 866.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 广东版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2010-09-25 12:42:00 | ||
图片预览








文档简介
课件24张PPT。牛顿第二定律的应用(四)——二力合成法与正交分解法课前热身:1.一辆小车在水平面上行驶,悬挂的摆球相对于小车静止,并且悬绳与竖直方向成θ角,如图
所示,下列关于小车的运动情况正确的是( )
A.加速度方向向左,大小为gtanθ
B.加速度方向向右,大小为gtanθ
C.加速度方向向左,大小为gsinθ
D.加速度方向向右,大小为gsinθ2.如图所示,质量为m的物体放在倾角为α的斜面上,物体和斜面间的动摩擦因数为μ,如沿斜面向上加一个力F,使物体沿斜面向上以加速度a做匀加速直线运动,则F为多少?Y方向:Fy=FN-Gy=0X方向:
Fx=F-GX-Ff=ma 二力合成法与正交分解法
1.二力合成法
运用牛顿定律解题时,如果物体只受两个力作用,若已知其中一个力的大小、方向和另一个力的方向,又知道加速度的方向,即合力的方向,就可以由二力合成的 定则,求出 的大小,另一分力的 以及物体的 .若已知物体的加速度,由牛顿定律求出物体的 ,又已知其中一个分力,可求另一分力的大小和方向.平行四边形合力大小加速度合力
2.正交分解法
所谓正交分解法是把一个矢量分解在两个互相
的坐标轴上的方法.
正交分解法是一种常用的矢量运算方法,也是解牛顿第二定律题目最基本的方法.物体在受到三个或是三个以上的不在同一直线上的力的作用时一般都采用正交分解法.垂直正交分解法的应用
1.正交分解法的基本步骤
第二步,将题目所给定的矢量和要求的各矢量沿x、y轴方向分解,求出各分量,凡与x、y轴方向一致的为正;凡与x、y轴反向的为负,标以“-”号,凡与轴垂直的矢量,该矢量在该轴上的分量为0.第一步,建立正交x、y坐标,这是最重要的一步,x、y坐标的建立,并不一定是水平与竖直方向,可根据问题方便来设定方向,不过x与y的方向一定是相互垂直.
第四步,根据各x、y轴的分量,求出该矢量的大小.
第三步,根据在各轴方向上的运动状态列方程,这样就把矢量运算转化为标量运算;对于多过程问题,若各阶段运动状态不同,应根据各阶段的状态,分阶段来列方程.2.正交分解法的表示方法
Fx合=F1x+F2x+F3x+…=max
Fy合=F1y+F2y+F3y+…=may3.为了减少矢量的分解,在建立坐标系时确定x轴的正方向一般有两种方法:
(2)分解加速度而不分解力.此法一般是以某个力的方向为x轴的正方向,而其他力都落在两个坐标上而不需要再分解.(1)分解力而不分解加速度.此时应规定加速度的方向为x轴的正方向.题型探究
题型1 二力合成法的应用
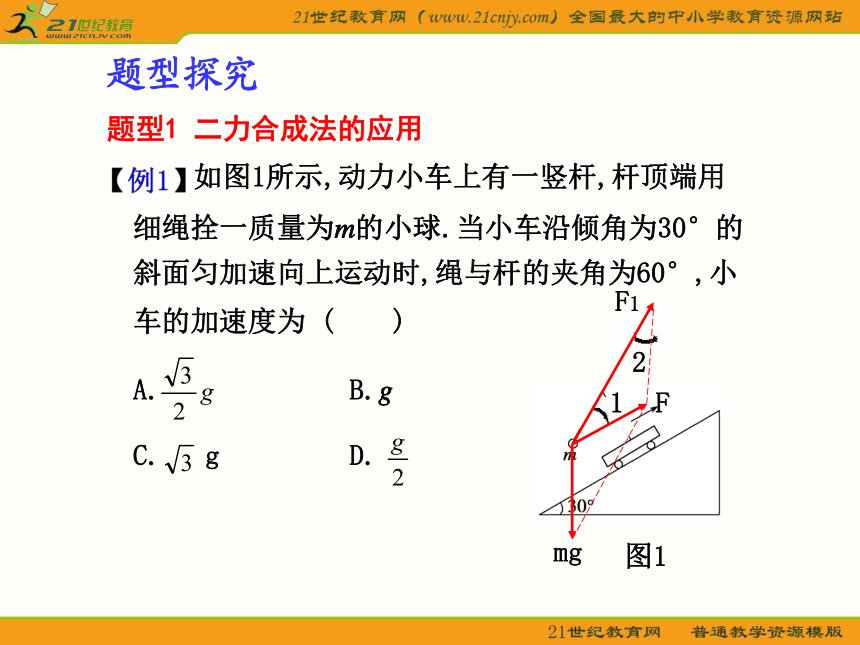
如图1所示,动力小车上有一竖杆,杆顶端用细绳拴一质量为m的小球.当小车沿倾角为30°的斜面匀加速向上运动时,绳与杆的夹角为60°,小车的加速度为 ( )
A. B.g
C. g D.图121解析 该问题中,小球受到两个不在同一直线上的力的作用,分析小球的受力后,画出受力图,用合成法求合力及绳子拉力,再用牛顿第二定律列方程求出加速度.
小球的受力及力的合成如右图所示
由几何关系可得:∠1=∠2=30°,所以
F=mg,由F=ma得a=g
答案 B方法提炼
对只受两个力作用的物体应用牛顿定律时,二力合成法比较简单.这个方法的关键点是确定加速度的方向,即合力的方向,以及确定两个分力的方向,这是做平行四边形的基础.变式练习1 一倾角为θ的斜面上放一木块,木块上固定一支架,支架末端用细绳悬挂一小球,木块在斜面上下滑时,小球与滑块相对静止共同运动,当细线(1)沿竖直方向;(2)与斜面方向垂直;(3)沿水平方向,求上述3种情况下滑块下滑的加速度(如图2所示).图2解析 (1)如图(a)所示,FT1与mg都是竖直方向,故不可能有加速度.FT1-mg=0,a=0,说明木块沿斜面匀速下滑.(2)如图(b)所示,FT2与mg的合力必为加速度方向,即沿斜面方向,做出平行四边形.可知F合=mgsinθ
由牛顿第二定律知a= =gsinθ
即加速度沿斜面向下,大小为gsinθ.
(3)由于细绳只能产生拉力且沿绳的方向,故小球受力情况如图(c)所示,由图可见F合=
即a= ,方向沿斜面向下.题型2 正交分解法的应用
如图所示, 传送带与地面的夹角θ=37°,从A到B长度16 m,在传送带上端A无初速度地放一个质量为m=0.5 kg的小物体,它与传送带之间的动摩擦因数为0.5.分别求出下列几种情形下物体从A运动到B所需时间是多少?
(1)若传送带静止不动;
(2)若传送带以10 m/s的速率顺时针转动
(3)若传送带以10 m/s的速率逆时针转动
思路点拨 做好对物体受力和运动过程的分析,并注意挖掘题目中的隐含条件.解析:>
(1)物体放在传送带上后,物体受沿斜面向上的摩擦力Ff,物体受力如图所示.由于mgsinθ μmgcosθ,mgsin-μmgcosθ=ma
解得a=g(sinθ-μcosθ)
=10×(0.6-0.5×0.8) m/s2
=2 m/s2即μ由牛顿第二定律得(2)物体放在顺时针转动的传送带上后,物体受沿斜面向上的滑动摩擦力Ff,物体受力如图所示.同样的由于mgsinθ>μmgcosθ,即μmgsinθ+μmgcosθ=ma1
解得a1=g(sinθ+μcosθ)=10×(0.6+0.5×0.8) m/s2
=10 m/s2(3)物体静止的放在逆时针转动的传送带上后,由于物体相对于传送带向上运动,所以刚开始物体受沿斜面向下的滑动摩擦力Ff, 物体受力如图所示.物体加速至与传送带速度相等需要的时间
t1=
t1时间内物体的位移s1=
因s1设后一阶段物体滑至B处所需时间为t2
则L-s1=vt2+ a2t22
解得t2=1 s(t2=-11 s,舍去)
所以物体由A到B的时间t=t1+t2=2 s.
答案 2 s而此时v1=a1t1=10m/s=v传由于mgsinθ>μmgcosθ,物体将继续加速下滑,(但是滑动摩擦力方向改变)物体受力如图所示.由牛顿第二定律得:mgsinθ-μmgcosθ=ma2解得a2=g(sinθ-μcosθ)
=10×(0.6-0.5×0.8) m/s2=2 m/s2例2:上题中若,物块下滑时间为多少?
解析:若,开始(即物块与传送带同速前)物体运动情况与上题相同,即,当物块与传送带同速后,由于,所以物块与传送带同速后与传送带一起做匀速运动,则,因此时间为:。评析:此题主要用来考查分析物理过程和物体的受力分析,运用牛顿第二定律和运动学基本规律来解题的能力,这是一道较好的广为采用的经典倾斜放置运行的传送带例题. 作业:1、 上题情形(3)中若 ,物块下滑时间为多少?
2、完成步步高讲义(p58)素能提升2、3、5、6、7、8
3、预习连接体问题谢谢各位领导、老师光临指导!
所示,下列关于小车的运动情况正确的是( )
A.加速度方向向左,大小为gtanθ
B.加速度方向向右,大小为gtanθ
C.加速度方向向左,大小为gsinθ
D.加速度方向向右,大小为gsinθ2.如图所示,质量为m的物体放在倾角为α的斜面上,物体和斜面间的动摩擦因数为μ,如沿斜面向上加一个力F,使物体沿斜面向上以加速度a做匀加速直线运动,则F为多少?Y方向:Fy=FN-Gy=0X方向:
Fx=F-GX-Ff=ma 二力合成法与正交分解法
1.二力合成法
运用牛顿定律解题时,如果物体只受两个力作用,若已知其中一个力的大小、方向和另一个力的方向,又知道加速度的方向,即合力的方向,就可以由二力合成的 定则,求出 的大小,另一分力的 以及物体的 .若已知物体的加速度,由牛顿定律求出物体的 ,又已知其中一个分力,可求另一分力的大小和方向.平行四边形合力大小加速度合力
2.正交分解法
所谓正交分解法是把一个矢量分解在两个互相
的坐标轴上的方法.
正交分解法是一种常用的矢量运算方法,也是解牛顿第二定律题目最基本的方法.物体在受到三个或是三个以上的不在同一直线上的力的作用时一般都采用正交分解法.垂直正交分解法的应用
1.正交分解法的基本步骤
第二步,将题目所给定的矢量和要求的各矢量沿x、y轴方向分解,求出各分量,凡与x、y轴方向一致的为正;凡与x、y轴反向的为负,标以“-”号,凡与轴垂直的矢量,该矢量在该轴上的分量为0.第一步,建立正交x、y坐标,这是最重要的一步,x、y坐标的建立,并不一定是水平与竖直方向,可根据问题方便来设定方向,不过x与y的方向一定是相互垂直.
第四步,根据各x、y轴的分量,求出该矢量的大小.
第三步,根据在各轴方向上的运动状态列方程,这样就把矢量运算转化为标量运算;对于多过程问题,若各阶段运动状态不同,应根据各阶段的状态,分阶段来列方程.2.正交分解法的表示方法
Fx合=F1x+F2x+F3x+…=max
Fy合=F1y+F2y+F3y+…=may3.为了减少矢量的分解,在建立坐标系时确定x轴的正方向一般有两种方法:
(2)分解加速度而不分解力.此法一般是以某个力的方向为x轴的正方向,而其他力都落在两个坐标上而不需要再分解.(1)分解力而不分解加速度.此时应规定加速度的方向为x轴的正方向.题型探究
题型1 二力合成法的应用
如图1所示,动力小车上有一竖杆,杆顶端用细绳拴一质量为m的小球.当小车沿倾角为30°的斜面匀加速向上运动时,绳与杆的夹角为60°,小车的加速度为 ( )
A. B.g
C. g D.图121解析 该问题中,小球受到两个不在同一直线上的力的作用,分析小球的受力后,画出受力图,用合成法求合力及绳子拉力,再用牛顿第二定律列方程求出加速度.
小球的受力及力的合成如右图所示
由几何关系可得:∠1=∠2=30°,所以
F=mg,由F=ma得a=g
答案 B方法提炼
对只受两个力作用的物体应用牛顿定律时,二力合成法比较简单.这个方法的关键点是确定加速度的方向,即合力的方向,以及确定两个分力的方向,这是做平行四边形的基础.变式练习1 一倾角为θ的斜面上放一木块,木块上固定一支架,支架末端用细绳悬挂一小球,木块在斜面上下滑时,小球与滑块相对静止共同运动,当细线(1)沿竖直方向;(2)与斜面方向垂直;(3)沿水平方向,求上述3种情况下滑块下滑的加速度(如图2所示).图2解析 (1)如图(a)所示,FT1与mg都是竖直方向,故不可能有加速度.FT1-mg=0,a=0,说明木块沿斜面匀速下滑.(2)如图(b)所示,FT2与mg的合力必为加速度方向,即沿斜面方向,做出平行四边形.可知F合=mgsinθ
由牛顿第二定律知a= =gsinθ
即加速度沿斜面向下,大小为gsinθ.
(3)由于细绳只能产生拉力且沿绳的方向,故小球受力情况如图(c)所示,由图可见F合=
即a= ,方向沿斜面向下.题型2 正交分解法的应用
如图所示, 传送带与地面的夹角θ=37°,从A到B长度16 m,在传送带上端A无初速度地放一个质量为m=0.5 kg的小物体,它与传送带之间的动摩擦因数为0.5.分别求出下列几种情形下物体从A运动到B所需时间是多少?
(1)若传送带静止不动;
(2)若传送带以10 m/s的速率顺时针转动
(3)若传送带以10 m/s的速率逆时针转动
思路点拨 做好对物体受力和运动过程的分析,并注意挖掘题目中的隐含条件.解析:>
(1)物体放在传送带上后,物体受沿斜面向上的摩擦力Ff,物体受力如图所示.由于mgsinθ μmgcosθ,mgsin-μmgcosθ=ma
解得a=g(sinθ-μcosθ)
=10×(0.6-0.5×0.8) m/s2
=2 m/s2即μ
解得a1=g(sinθ+μcosθ)=10×(0.6+0.5×0.8) m/s2
=10 m/s2(3)物体静止的放在逆时针转动的传送带上后,由于物体相对于传送带向上运动,所以刚开始物体受沿斜面向下的滑动摩擦力Ff, 物体受力如图所示.物体加速至与传送带速度相等需要的时间
t1=
t1时间内物体的位移s1=
因s1
则L-s1=vt2+ a2t22
解得t2=1 s(t2=-11 s,舍去)
所以物体由A到B的时间t=t1+t2=2 s.
答案 2 s而此时v1=a1t1=10m/s=v传由于mgsinθ>μmgcosθ,物体将继续加速下滑,(但是滑动摩擦力方向改变)物体受力如图所示.由牛顿第二定律得:mgsinθ-μmgcosθ=ma2解得a2=g(sinθ-μcosθ)
=10×(0.6-0.5×0.8) m/s2=2 m/s2例2:上题中若,物块下滑时间为多少?
解析:若,开始(即物块与传送带同速前)物体运动情况与上题相同,即,当物块与传送带同速后,由于,所以物块与传送带同速后与传送带一起做匀速运动,则,因此时间为:。评析:此题主要用来考查分析物理过程和物体的受力分析,运用牛顿第二定律和运动学基本规律来解题的能力,这是一道较好的广为采用的经典倾斜放置运行的传送带例题. 作业:1、 上题情形(3)中若 ,物块下滑时间为多少?
2、完成步步高讲义(p58)素能提升2、3、5、6、7、8
3、预习连接体问题谢谢各位领导、老师光临指导!
同课章节目录
- 第一章 运动的描述
- 第一节 认识运动
- 第二节 时间 位移
- 第三节 记录物体的运动信息
- 第四节 物体运动的速度
- 第五节 速度变化的快慢 加速度
- 第六节 用图象描述直线运动
- 第二章 探究匀变速直线运动规律
- 第一节 探究自由落体运动
- 第二节 自由落体运动规律
- 第三节 从自由落体到匀变速直线运动
- 第四节 匀变速直线运动与汽车行驶安全
- 第三章 研究物体间的相互作用
- 第一节 探究形变与弹力的关系
- 第二节 研究摩擦力
- 第三节 力的等效和替代
- 第四节 力的合成与分解
- 第五节 共点力的平衡条件
- 第六节 作用力与反作用力
- 第四章 力与运动
- 第一节 伽利略的理想实验与牛顿第一定律
- 第二节 影响加速度的因素
- 第三节 探究物体运动与受力的关系
- 第四节 牛顿第二定律
- 第五节 牛顿第二定律的应用
- 第六节 超重和失重
- 第七节 力学单位
