第一章 三角形单元检测题(含答案)
图片预览

文档简介
第一单元三角形测试题
一、选择题(每小题4分,共28分)
1.下列长度的三条线段不能组成三角形的是( )
A.5,5,10 B.4,5,6 C.4,4,4 D.3,4,5
2.(2018·潍坊昌乐期中)全等形是指( )
A.形状相同的两个图形 B.面积相同的两个图形
C.两张中国地形图,两个等腰三角形都是全等形 D.能够完全重合的两个平面图形
3.(2018·邓州市期中)已知,如图△ABC≌△ADE,AE=AC,∠CAE=20°,则∠BED的度数为( )
A.60° B.90 C.80 D.20°
4.(2018·济宁金乡期中)已知∠ACD=∠BCD,那么添加下列一个条件后,仍无法判定△ACD≌△BCD的是( )
A.∠A=∠B B.∠ADC=∠BDC C AC=BC D AD=BD
5.(2018·栖霞期中)根据下列已知条件,能够画出唯一△ABC的是( )
A.AB=5,BC=6,∠A=70° B AB=5, BC=6,AC=13
C.∠A=50°,∠B=80°,AB=8 D.∠A=40°,∠B=50°,∠C=90
6.(2018·潍坊昌乐期中)如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.4个 B.3个 C.2个 D.1个
7.(2018·湖州月考)如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面B积等于( )
A.10 B.7 C.5 D.4
二、填空题(每小题5分,共25分)
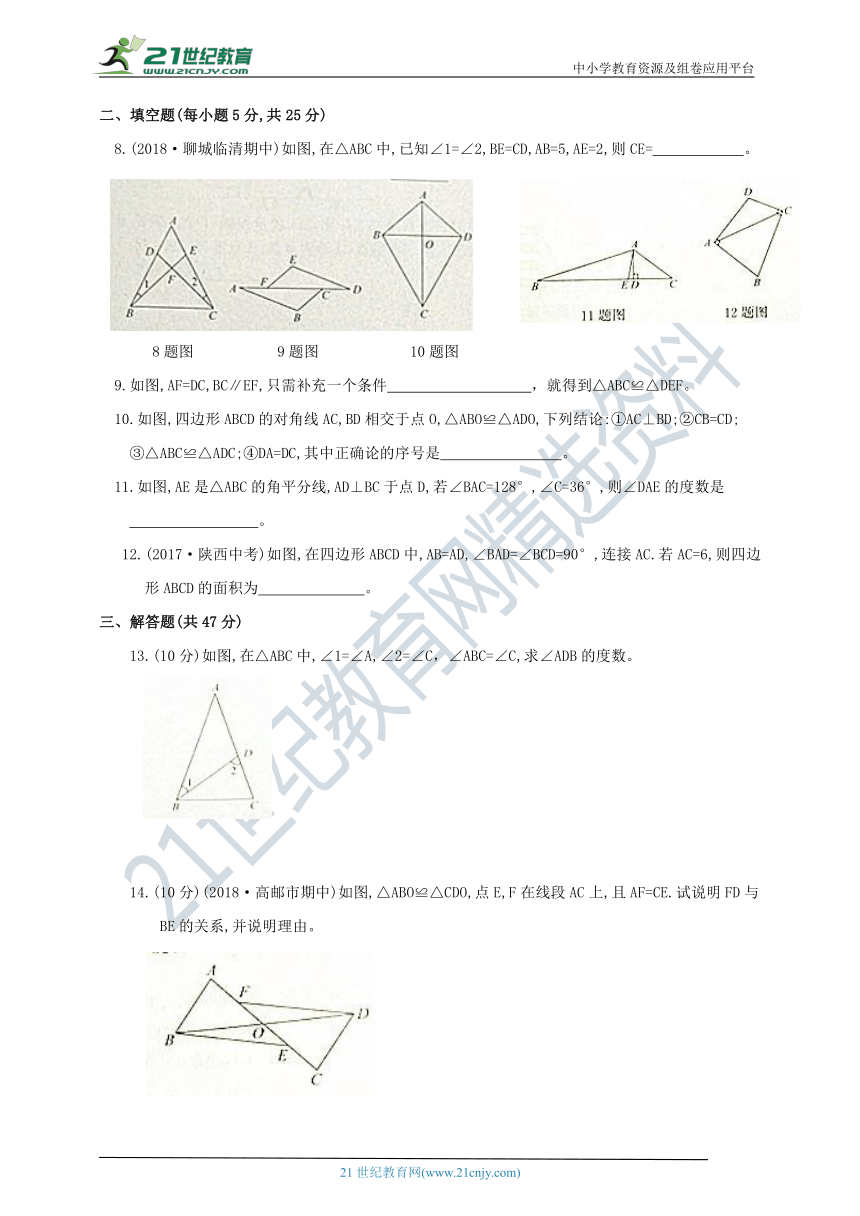
8.(2018·聊城临清期中)如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE= 。
8题图 9题图 10题图
9.如图,AF=DC,BC∥EF,只需补充一个条件 ,就得到△ABC≌△DEF。
10.如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO,下列结论:①AC⊥BD;②CB=CD;
③△ABC≌△ADC;④DA=DC,其中正确论的序号是 。
11.如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE的度数是
。
12.(2017·陕西中考)如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为 。
三、解答题(共47分)
13.(10分)如图,在△ABC中,∠1=∠A,∠2=∠C,∠ABC=∠C,求∠ADB的度数。
14.(10分)(2018·高邮市期中)如图,△ABO≌△CDO,点E,F在线段AC上,且AF=CE.试说明FD与BE的关系,并说明理由。
15.(13分)(2018·聊城临清期中)王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离。
16.(14分)复习“全等三角形”的知识时,老师布置了一道作业题:“如图①,已知在△ABC中,AB=AC,点P是△ABC内部任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,试说明BQ=CP.”
赵小亮是个爱动脑筋的同学,他通过对图①的分析,验证了△ABQ≌△ACP,从而证得BQ=CP之后,将点P移到△ABC之外,原题中的条件不变,发现“BQ=CP”仍然成立,请你就图②给出说明。
参考答案及解析
1.A 2.D 3.D 4.D 5.C 6.B 7.C 8.3
9.EF=BC或∠E=∠B或∠A=∠D或AB∥DE
10.① ② ③
11.10o 12.18.
13.解:设∠1=x,因为∠1=∠A
所以∠A=x,∠2=∠1+∠A=2x。
因为∠2=∠C,∠ABC=∠C,所以∠ABC=∠C=2X,
所以x+2x+2x=180°,解得x=36°,
所以∠2=2x=72
所以∠ADB=180°-72°=108°
14.解:FD=BE,FD∥BE。
理由如下:因为△ABO≌△CDO,所以OA=OC, OB=OD,
因为AF=CE,所以OE=OF,在△DOF和△BOE中 OF=OE,∠DOF=∠BOE,OD=OB,
所以△DOF≌△BOE,所以FD=BE,∠FDO=∠EBO,所以FD∥BE。
15.解:由题意得:AC=BC,∠ACB=90o, AD⊥DE,BE⊥DE,
所以∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,所以∠BCE=∠DAC,
在△ADC和△CEB中∠ADC=∠CEB,∠DAC=∠BCE,AC=BC,
所以△ADC≌△CEB(AAS).
由题意得AD=EC=6cm,DC=BE= 14cm,所以DE=DC+CE=20(cm)
答:两堵木墙之间的距离为20cm
16.解:因为∠QAP=∠BAC,所以∠QAP+∠BAP=∠BAC+∠BAP,
即∠QAB=∠PAC,在△QAB和△PAC中 AQ=AP,∠QAB=∠PAC,AB=AC,
所以△QAB≌△PAC,所以BQ=CP.
一、选择题(每小题4分,共28分)
1.下列长度的三条线段不能组成三角形的是( )
A.5,5,10 B.4,5,6 C.4,4,4 D.3,4,5
2.(2018·潍坊昌乐期中)全等形是指( )
A.形状相同的两个图形 B.面积相同的两个图形
C.两张中国地形图,两个等腰三角形都是全等形 D.能够完全重合的两个平面图形
3.(2018·邓州市期中)已知,如图△ABC≌△ADE,AE=AC,∠CAE=20°,则∠BED的度数为( )
A.60° B.90 C.80 D.20°
4.(2018·济宁金乡期中)已知∠ACD=∠BCD,那么添加下列一个条件后,仍无法判定△ACD≌△BCD的是( )
A.∠A=∠B B.∠ADC=∠BDC C AC=BC D AD=BD
5.(2018·栖霞期中)根据下列已知条件,能够画出唯一△ABC的是( )
A.AB=5,BC=6,∠A=70° B AB=5, BC=6,AC=13
C.∠A=50°,∠B=80°,AB=8 D.∠A=40°,∠B=50°,∠C=90
6.(2018·潍坊昌乐期中)如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.4个 B.3个 C.2个 D.1个
7.(2018·湖州月考)如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面B积等于( )
A.10 B.7 C.5 D.4
二、填空题(每小题5分,共25分)
8.(2018·聊城临清期中)如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE= 。
8题图 9题图 10题图
9.如图,AF=DC,BC∥EF,只需补充一个条件 ,就得到△ABC≌△DEF。
10.如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO,下列结论:①AC⊥BD;②CB=CD;
③△ABC≌△ADC;④DA=DC,其中正确论的序号是 。
11.如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE的度数是
。
12.(2017·陕西中考)如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为 。
三、解答题(共47分)
13.(10分)如图,在△ABC中,∠1=∠A,∠2=∠C,∠ABC=∠C,求∠ADB的度数。
14.(10分)(2018·高邮市期中)如图,△ABO≌△CDO,点E,F在线段AC上,且AF=CE.试说明FD与BE的关系,并说明理由。
15.(13分)(2018·聊城临清期中)王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离。
16.(14分)复习“全等三角形”的知识时,老师布置了一道作业题:“如图①,已知在△ABC中,AB=AC,点P是△ABC内部任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,试说明BQ=CP.”
赵小亮是个爱动脑筋的同学,他通过对图①的分析,验证了△ABQ≌△ACP,从而证得BQ=CP之后,将点P移到△ABC之外,原题中的条件不变,发现“BQ=CP”仍然成立,请你就图②给出说明。
参考答案及解析
1.A 2.D 3.D 4.D 5.C 6.B 7.C 8.3
9.EF=BC或∠E=∠B或∠A=∠D或AB∥DE
10.① ② ③
11.10o 12.18.
13.解:设∠1=x,因为∠1=∠A
所以∠A=x,∠2=∠1+∠A=2x。
因为∠2=∠C,∠ABC=∠C,所以∠ABC=∠C=2X,
所以x+2x+2x=180°,解得x=36°,
所以∠2=2x=72
所以∠ADB=180°-72°=108°
14.解:FD=BE,FD∥BE。
理由如下:因为△ABO≌△CDO,所以OA=OC, OB=OD,
因为AF=CE,所以OE=OF,在△DOF和△BOE中 OF=OE,∠DOF=∠BOE,OD=OB,
所以△DOF≌△BOE,所以FD=BE,∠FDO=∠EBO,所以FD∥BE。
15.解:由题意得:AC=BC,∠ACB=90o, AD⊥DE,BE⊥DE,
所以∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,所以∠BCE=∠DAC,
在△ADC和△CEB中∠ADC=∠CEB,∠DAC=∠BCE,AC=BC,
所以△ADC≌△CEB(AAS).
由题意得AD=EC=6cm,DC=BE= 14cm,所以DE=DC+CE=20(cm)
答:两堵木墙之间的距离为20cm
16.解:因为∠QAP=∠BAC,所以∠QAP+∠BAP=∠BAC+∠BAP,
即∠QAB=∠PAC,在△QAB和△PAC中 AQ=AP,∠QAB=∠PAC,AB=AC,
所以△QAB≌△PAC,所以BQ=CP.
