第三章单元测试-2018-2019学年高一数学单元巩固练习(必修1)
文档属性
| 名称 | 第三章单元测试-2018-2019学年高一数学单元巩固练习(必修1) |  | |
| 格式 | zip | ||
| 文件大小 | 563.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-23 09:54:48 | ||
图片预览




文档简介
(测试时间:120分钟 满分:150分)
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数的零点所在的区间是( )
A. B. C. D.
【答案】B
2.已知函数,那么在下列区间中含有函数零点的是( )
A. B. C. D.
【答案】B
【解析】
因为函数,是连续单调函数,
且
,
∴函数f(x)在区间必有零点,故选B.
3.已知实数,若函数的零点所在区间为,则的取值范围是( )
A. B. C. D.
【答案】D
【解析】
4.某企业为节能减排,用万元购进一台新设备用于生产.第一年需运营费用万元,从第二年起,每年运营费用均比上一年增加万元,该设备每年生产的收入均为万元.设该设备使用了年后,年平均盈利额达到最大值(盈利额等于收入减去成本),则等于( )
A. B. C. D.
【答案】D
【解析】
设该设备第n年的营运费为万元,
则数列是以2为首项,2为公差的等差数列,则,
则该设备使用n年的营运费用总和为,
设第n年的盈利总额为,则,
年平均盈利额,
当时,年平均盈利额取得最大值4.
故选:D.
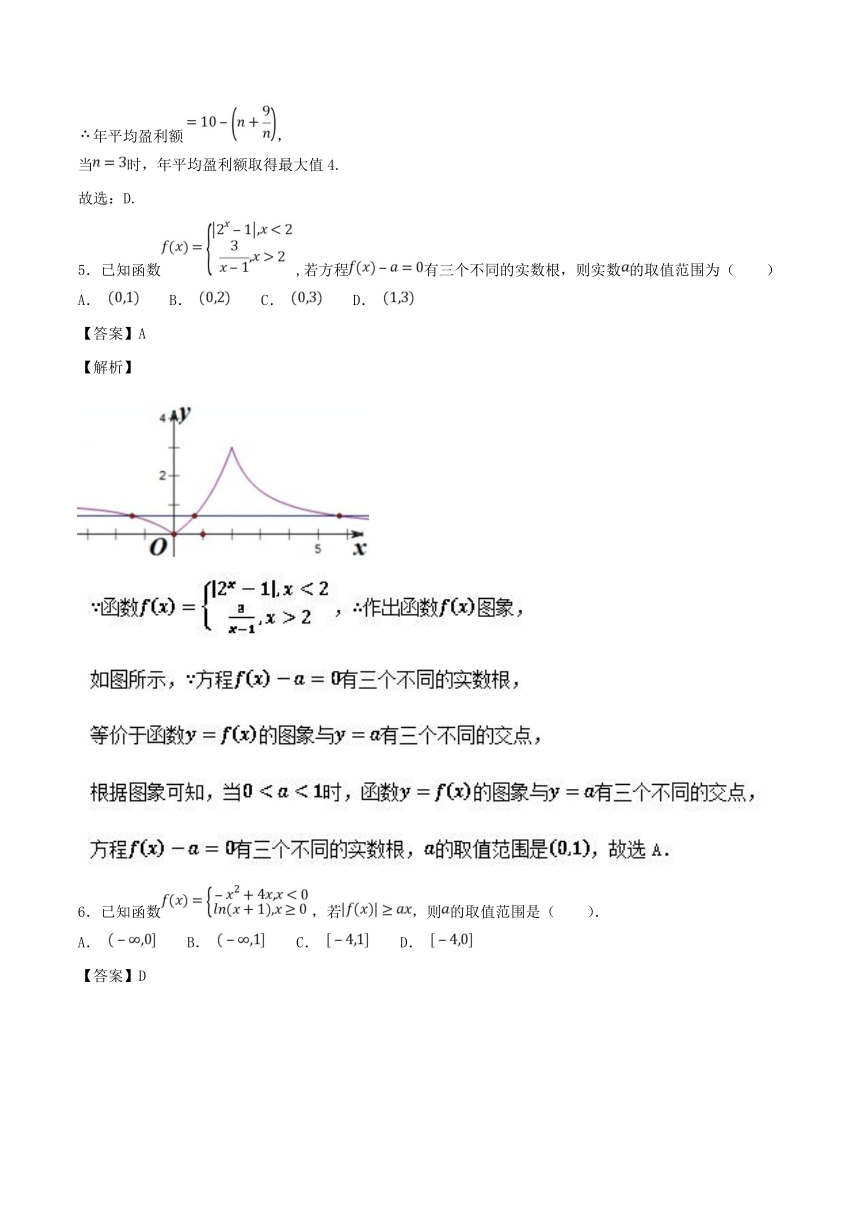
5.已知函数,若方程有三个不同的实数根,则实数的取值范围为( )
A. B. C. D.
【答案】A
【解析】
6.已知函数,若,则的取值范围是( ).
A. B. C. D.
【答案】D
7.关于的方程在区间内有两个不等实根,则实数的取值范围是( )
A. B. C. D.
【答案】C
【解析】
设,由题意,解得.
故选C.
8.已知函数,则使函数有零点的实数的取值范围是( )
A. B.
C. D.
【答案】D
【解析】
9.已知函数 ,则关于x的方程在上的根的个数为( )
A. 3 B. 4 C. 5 D. 6
【答案】B
【解析】
当时,,
所以.
当,,
故,
当时,可化为,
解得或,
因,,故在有且只有一个解.
当时,可化为,
解得或,
10.若,分别是函数,的零点,则下列结论成立的是( )
A. B. C. D.
【答案】D
【解析】
由,得,
其根就是直线与曲线交点的横坐标,
由,得,
其根就是直线与曲线交点的横坐标,
因为的图象关于对称,
且曲线与曲线关于对称,
所以与关于对称,
又
可得,故选D.
11.,若方程无实根,则方程( )
A. 有四个相异实根 B. 有两个相异实根
C. 有一个实根 D. 无实数根
【答案】D
12.已知函数,函数有四个不同的零点,从小到大依次为
则的取值范围为( )
A. B. C. D.
【答案】A
【解析】
根据题中所给的函数解析式,画出函数的图像,
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.我国古代数学著作《张邱建算经》中记载百鸡问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一。凡百钱,买鸡百只,问鸡翁、母、雏各几何?”设鸡翁,鸡母,鸡雏个数分别为,,,则当时,___________,___________.
【答案】811
【解析】
故答案为(1). 8 (2). 11
14.已知函数其中,若函数的图象上恰好有两对关于y轴对称的点,则实数的取值范围为____.
【答案】
15.对于实数a,b,定义运算“*”:a*b=,设f (x)=(x-4)*,若关于x的方程|f (x)-m|=1(m∈R)恰有四个互不相等的实数根,则实数m的取值范围是________.
【答案】(-1,1)∪(2,4)
【解析】
解不等式x﹣4≤﹣4得x≥0,f(x)=,
画出函数f(x)的大致图象如图所示.
因为关于x的方程|f(x)﹣m|=1(m∈R),即f(x)=m±1(m∈R)恰有四个互不相等的实数根,
所以两直线y=m±1(m∈R)与曲线y=f(x)共有四个不同的交点,
∴或或,
解得2<m<4或﹣1<m<1.
故答案为(﹣1,1)∪(2,4).
16.已知a∈R,函数若对任意x∈[–3,+),f(x)≤恒成立,则a的取值范围是__________.
【答案】[,2]
②当时,即:,整理可得:,
由恒成立的条件可知:,
结合二次函数的性质可知:
当或时,,则;
综合①②可得的取值范围是.
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题10分)某农家旅游公司有客房300间,每间日房租为20元,每天客都满.公司欲提高档次,并提高租金.根据市场调查:如果每间日房租每增加2元,客房出租数就会减少10间.请你根据以上信息回答下列问题.
(1)当客房租金提高到每间日房租28元时,相应的客房出租数变为多少,当日所获租金是多少?
(2)若不考虑其他因素,则该旅游公司将房间租金提高到多少时,每天客房所获租金最多?最多是多少?
【答案】(1)7280(2)8000
18.(本小题12分)函数和的图像的示意图如图所示,设两函数的图像交于点,,且.
(1)设曲线,分别对应函数和,请指出图中曲线,对应的函数解析式,若不等式对任意恒成立,求的取值范围;
(2)若,,且、 ,求、的值.
【答案】(1)答案见解析;(2),.
(2)令,则,为函数的零点,
由于,,,,
则方程的两个零点,,
因此整数,.
19.(本小题12分)已知函数
(1)求函数的零点的集合;
(2)记函数的值域为,函数的定义域为,且,求实数的取值范围.
【答案】(1) .(2) .
【解析】
(1)令,则,
函数零点的集合为.
20.(本小题12分)某公司为提高员工的综合素质,聘请专业机构对员工进行专业技术培训,其中培训机构费用成本为12000元.公司每位员工的培训费用按以下方式与该机构结算:若公司参加培训的员工人数不超过30人时,每人的培训费用为850元;若公司参加培训的员工人数多于30人,则给予优惠:每多一人,培训费减少10元.已知该公司最多有60位员工可参加培训,设参加培训的员工人数为人,每位员工的培训费为元,培训机构的利润为元.
(1)写出与 之间的函数关系式;
(2)当公司参加培训的员工为多少人时,培训机构可获得最大利润?并求最大利润.
【答案】(1);(2)
【解析】
(1)依题意得,当时,;
当时,.
.
当或时, 取得最大值.
因为,
当公司参加培训的员工人数为或时,
培训机构可获得最大利润元.
21.(本小题12分)已知函数.
()求函数的零点.
()求函数在区间上的最大值和最小值.
()已知,求满足不等式的的取值范围.
【答案】()和;(),;().
【解析】
(),
∴的零点为和.
(),
∴在上单调递减,
在上单调递增,
∴时,
,
.
(),
,
∴,
即,
∴,
∴或。
22.(本小题12分)已知函数.
(Ⅰ)设,求方程的根;
(Ⅱ)设,函数,已知时存在使得.若有且只有一个零点,求b的值.
【答案】(1)(2)
(Ⅱ)当时,
因为
当且仅当时取等号
所以是的唯一的零点
且,由零点存在定理知在(-2,,)必存在另一零点
此时,存在2个零点,不符合题意
综上可得.
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数的零点所在的区间是( )
A. B. C. D.
【答案】B
2.已知函数,那么在下列区间中含有函数零点的是( )
A. B. C. D.
【答案】B
【解析】
因为函数,是连续单调函数,
且
,
∴函数f(x)在区间必有零点,故选B.
3.已知实数,若函数的零点所在区间为,则的取值范围是( )
A. B. C. D.
【答案】D
【解析】
4.某企业为节能减排,用万元购进一台新设备用于生产.第一年需运营费用万元,从第二年起,每年运营费用均比上一年增加万元,该设备每年生产的收入均为万元.设该设备使用了年后,年平均盈利额达到最大值(盈利额等于收入减去成本),则等于( )
A. B. C. D.
【答案】D
【解析】
设该设备第n年的营运费为万元,
则数列是以2为首项,2为公差的等差数列,则,
则该设备使用n年的营运费用总和为,
设第n年的盈利总额为,则,
年平均盈利额,
当时,年平均盈利额取得最大值4.
故选:D.
5.已知函数,若方程有三个不同的实数根,则实数的取值范围为( )
A. B. C. D.
【答案】A
【解析】
6.已知函数,若,则的取值范围是( ).
A. B. C. D.
【答案】D
7.关于的方程在区间内有两个不等实根,则实数的取值范围是( )
A. B. C. D.
【答案】C
【解析】
设,由题意,解得.
故选C.
8.已知函数,则使函数有零点的实数的取值范围是( )
A. B.
C. D.
【答案】D
【解析】
9.已知函数 ,则关于x的方程在上的根的个数为( )
A. 3 B. 4 C. 5 D. 6
【答案】B
【解析】
当时,,
所以.
当,,
故,
当时,可化为,
解得或,
因,,故在有且只有一个解.
当时,可化为,
解得或,
10.若,分别是函数,的零点,则下列结论成立的是( )
A. B. C. D.
【答案】D
【解析】
由,得,
其根就是直线与曲线交点的横坐标,
由,得,
其根就是直线与曲线交点的横坐标,
因为的图象关于对称,
且曲线与曲线关于对称,
所以与关于对称,
又
可得,故选D.
11.,若方程无实根,则方程( )
A. 有四个相异实根 B. 有两个相异实根
C. 有一个实根 D. 无实数根
【答案】D
12.已知函数,函数有四个不同的零点,从小到大依次为
则的取值范围为( )
A. B. C. D.
【答案】A
【解析】
根据题中所给的函数解析式,画出函数的图像,
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.我国古代数学著作《张邱建算经》中记载百鸡问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一。凡百钱,买鸡百只,问鸡翁、母、雏各几何?”设鸡翁,鸡母,鸡雏个数分别为,,,则当时,___________,___________.
【答案】811
【解析】
故答案为(1). 8 (2). 11
14.已知函数其中,若函数的图象上恰好有两对关于y轴对称的点,则实数的取值范围为____.
【答案】
15.对于实数a,b,定义运算“*”:a*b=,设f (x)=(x-4)*,若关于x的方程|f (x)-m|=1(m∈R)恰有四个互不相等的实数根,则实数m的取值范围是________.
【答案】(-1,1)∪(2,4)
【解析】
解不等式x﹣4≤﹣4得x≥0,f(x)=,
画出函数f(x)的大致图象如图所示.
因为关于x的方程|f(x)﹣m|=1(m∈R),即f(x)=m±1(m∈R)恰有四个互不相等的实数根,
所以两直线y=m±1(m∈R)与曲线y=f(x)共有四个不同的交点,
∴或或,
解得2<m<4或﹣1<m<1.
故答案为(﹣1,1)∪(2,4).
16.已知a∈R,函数若对任意x∈[–3,+),f(x)≤恒成立,则a的取值范围是__________.
【答案】[,2]
②当时,即:,整理可得:,
由恒成立的条件可知:,
结合二次函数的性质可知:
当或时,,则;
综合①②可得的取值范围是.
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题10分)某农家旅游公司有客房300间,每间日房租为20元,每天客都满.公司欲提高档次,并提高租金.根据市场调查:如果每间日房租每增加2元,客房出租数就会减少10间.请你根据以上信息回答下列问题.
(1)当客房租金提高到每间日房租28元时,相应的客房出租数变为多少,当日所获租金是多少?
(2)若不考虑其他因素,则该旅游公司将房间租金提高到多少时,每天客房所获租金最多?最多是多少?
【答案】(1)7280(2)8000
18.(本小题12分)函数和的图像的示意图如图所示,设两函数的图像交于点,,且.
(1)设曲线,分别对应函数和,请指出图中曲线,对应的函数解析式,若不等式对任意恒成立,求的取值范围;
(2)若,,且、 ,求、的值.
【答案】(1)答案见解析;(2),.
(2)令,则,为函数的零点,
由于,,,,
则方程的两个零点,,
因此整数,.
19.(本小题12分)已知函数
(1)求函数的零点的集合;
(2)记函数的值域为,函数的定义域为,且,求实数的取值范围.
【答案】(1) .(2) .
【解析】
(1)令,则,
函数零点的集合为.
20.(本小题12分)某公司为提高员工的综合素质,聘请专业机构对员工进行专业技术培训,其中培训机构费用成本为12000元.公司每位员工的培训费用按以下方式与该机构结算:若公司参加培训的员工人数不超过30人时,每人的培训费用为850元;若公司参加培训的员工人数多于30人,则给予优惠:每多一人,培训费减少10元.已知该公司最多有60位员工可参加培训,设参加培训的员工人数为人,每位员工的培训费为元,培训机构的利润为元.
(1)写出与 之间的函数关系式;
(2)当公司参加培训的员工为多少人时,培训机构可获得最大利润?并求最大利润.
【答案】(1);(2)
【解析】
(1)依题意得,当时,;
当时,.
.
当或时, 取得最大值.
因为,
当公司参加培训的员工人数为或时,
培训机构可获得最大利润元.
21.(本小题12分)已知函数.
()求函数的零点.
()求函数在区间上的最大值和最小值.
()已知,求满足不等式的的取值范围.
【答案】()和;(),;().
【解析】
(),
∴的零点为和.
(),
∴在上单调递减,
在上单调递增,
∴时,
,
.
(),
,
∴,
即,
∴,
∴或。
22.(本小题12分)已知函数.
(Ⅰ)设,求方程的根;
(Ⅱ)设,函数,已知时存在使得.若有且只有一个零点,求b的值.
【答案】(1)(2)
(Ⅱ)当时,
因为
当且仅当时取等号
所以是的唯一的零点
且,由零点存在定理知在(-2,,)必存在另一零点
此时,存在2个零点,不符合题意
综上可得.
