专题08 函数模型与应用-2018-2019学年高一数学单元巩固练习(必修1)
文档属性
| 名称 | 专题08 函数模型与应用-2018-2019学年高一数学单元巩固练习(必修1) |

|
|
| 格式 | zip | ||
| 文件大小 | 813.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-23 00:00:00 | ||
图片预览




文档简介
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.四位好朋友在一次聚会上,他们按照各自的爱好选择了形状不同、内容高度相等、杯口半径相等的圆口酒杯,如下图所示,盛满酒后他们约定:先各自饮杯中酒的一半,设剩余酒的高度从左到右依次为,则它们的大小关系正确的是( )
A. B. C. D.
【答案】A
【解析】观察图形可知体积减少一半后剩余酒的高度最高为,最低为,故选A.
2.某商店按每件80元的价格购进某种时装1000件,根据市场预测,当每件售价100元时,可全售完;定价每提高1元,销售量就减少5件,若要获得最大利润,则售价应定为( )
A.110元 B.130元 C.150元 D.190元
【答案】C
3. 研究表明,当死亡生物组织内的碳14的含量不足死亡前的千分之一时,用一般的放射性探测器就测不到碳14了.若某一死亡生物组织内的碳14经过个“半衰期”后用一般的放射性探测器测不到碳14了,则的最小值是( )
(A)9 (B)10 (C)11 (D)12
【答案】B
【解析】由题可得函数关系式:,测.不到碳14了需小于千分之一时,
则当n=10时, 。
4.某公司为激励创新,计划逐年加大研发资金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是(参考数据:lg1.12≈0.05,lg1.3≈0.11,lg2≈0.30)( )
(A)2018年 (B)2019年 (C)2020年 (D)2021年
【答案】B
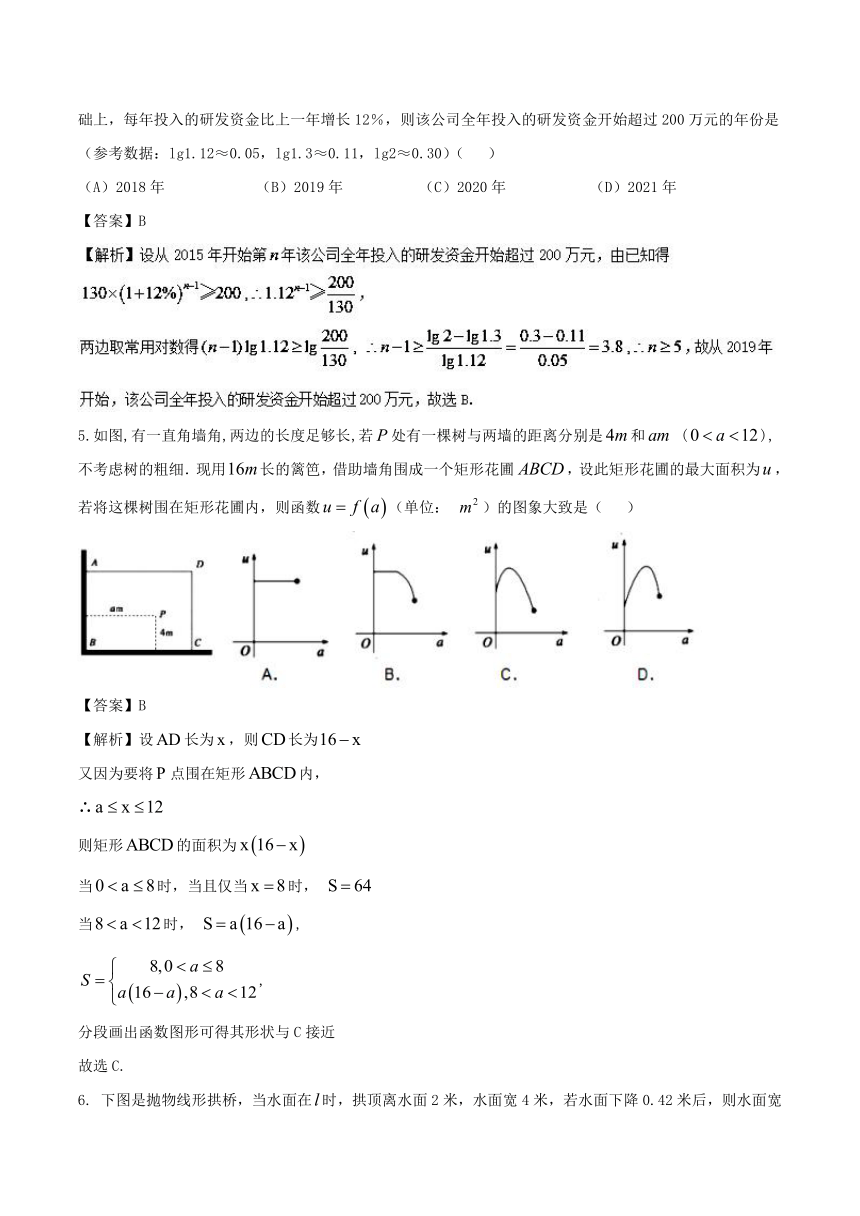
5.如图,有一直角墙角,两边的长度足够长,若处有一棵树与两墙的距离分别是和 (),不考虑树的粗细.现用长的篱笆,借助墙角围成一个矩形花圃,设此矩形花圃的最大面积为,若将这棵树围在矩形花圃内,则函数(单位: )的图象大致是( )
【答案】B
【解析】设长为,则长为 又因为要将点围在矩形内, ∴ 则矩形的面积为 当时,当且仅当时, 当时, ,
,
分段画出函数图形可得其形状与C接近 故选C.
6. 下图是抛物线形拱桥,当水面在时,拱顶离水面2米,水面宽4米,若水面下降0.42米后,则水面宽为( )
(A)2.2米 (B)4.4米 (C)2.4米 (D)4米
【答案】B
7.如图, 有四个平面图形分别是三角形、平行四边形、直角梯形、圆,垂直于轴的直线经过原点向右平行移动, 在移动过程中扫过平面图形的面积为(图中阴影部分), 若函数 的大致图象如图, 那么平面图形的形状不可能是( )
【答案】C
【解析】
试题分析:由函数图象可知,阴影部分的面积随的增大而增大,图象都是曲线,故选项A、B、D符合函数的图象,而C中刚开始的图象符合,到到梯形上底边时图象符合一次函数的图象,故选C.
8.根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为(A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是( )
A.75,25 B.75,16 C.60,25 D.60,16
【答案】D
9.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选1名代表,那么各班可推选人数与该班人数之间的函数关系用取整函数(表示不大于的最大整数)可以表示为( )
A. B.
C. D.
【答案】B
【解析】根据规定每人推选一名代表,当各班人数除以的余数大于时增加一名代表,即余数分别为时可以增选一名代表,也就是要进一位,所以最小应该加,因此利用取整函数可表示为,也可以用特殊取值法,若,排除C,D,若,排除A,故选B.
10.将甲桶中的升水缓慢注入空桶乙中,后甲桶剩余的水量符合指数衰减曲线.假设过后甲桶和乙桶的水量相等,若再过甲桶中的水只有升,则的值为( )
A.5 B.8
C.8 D.10
【答案】A
11. 出租车按如下方法收费:起步价7元,可行3(不含3);3到7(不含7)按元/计价(不足1按1计算);7以后按元/计价,到目的地结算时还需付1元的燃油附加费.若从甲地坐出租车到乙地(路程),需付车费(精确到1元) ( )
A、28元 B、27元 C、26元 D、25元
【答案】C
【解析】因为根据已知条件可知费用满足分段函数,所以需付车费
12. 衣柜里的樟脑丸,随着时间会挥发而体积缩小,刚放进的新丸体积为,经过天后体积与天数的关系式为:,若新丸经过50天后,体积变为;若一个新丸体积变为,则需经过的天数为
A.75天 B.100天 C.125天 D.150天
【答案】A.
【解析】由题意,得,解得;令,即,
即需经过的天数为75天.
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.抽气机每次抽出容器内空气的50%,则至少要抽__________次才能使容器内剩下的空气少于原来的0.1%.(参考数据:,)
【答案】
【解析】
设至少抽次,则由题意 即:,
两边取对数得,,即 ,
∴即至少要抽次.
14. 把物体放在冷空气中冷却,如果物体原来的温度是,空气的温度是,后物体的温度可由公式求得.把温度是的物体,放在的空气中冷却后,物体的温度是,那么的值约等于 .(保留三位有效数字,参考数据:取,取)
【答案】
【解析】依题意将代入公式可得,解得,.
15.某电脑公司2015年的各项经营收入中,经营电脑配件的收入为400万元,占全年经营总收入的40%.该公司预计2017年经营总收入要达到1 690万元,且计划从2015年到2017年,每年经营总收入的年增长率相同,2016年预计经营总收入为________万元.
【答案】1300
16.如图所示是某受污染的湖泊在自然净化过程中某种有害物质的剩留量y与净化时间t(月)的近似函数关系:y=at(t≥0,a>0且a≠1)的图象.有以下叙述:
①第4个月时,剩留量就会低于;
②每月减少的有害物质量都相等;
③若剩留量为, , 时,所经过的时间分别是t1,t2,t3,则t1+t2=t3.
其中所有正确叙述的序号是________.
【答案】①③
答案:①③.
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题10分)某食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)满足函数关系(e=2.718…为自然对数的底数,k,b为常数).若该食品在0℃的保鲜时间为192小时,在22℃的保鲜时间是48小时,求该食品在33℃的保鲜时间.
【答案】24小时.
【解析】
试题分析:由已知中保鲜时间与储藏温度是一种指数型关系,由已知构造方程组,
解得:;当时,运用指数幂的运算性质求解即可.
试题解析:由题意知,
,
.
所以当时,.
答:该食品在33℃的保鲜时间为24小时.
18.(本小题12分)某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在如下图象中的两条线段上.该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示:
(1)根据提供的图象,写出该种股票每股的交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少?
【答案】(1) (2) (3) 在30天中的第15天,日交易额的最大值为125万元
试题解析:(1)由图像知,前20天满足的是递增的直线方程,且过两点(0,2),(20,6),容易求得;从20天到30天满足递减的直线方程,且过两点(20,6),(30,5),求得方程为,
故P(元)与时间t(天)所满足的函数关系式为:
。。。。。。。。。。。。。。。4分
(2)由图表,易知Q与t满足一次函数关系,
即. ................7分
(3)由(1)(2)可知
.........................9分
当,t=15时,. .......................10分
当时,y随t的增大而减小. .........................11分
所以,在30天中的第15天,日交易额的最大值为125万元. .......12分
19.(本小题12分)某厂借嫦娥奔月的东风,推出品牌为“玉兔”的新产品,生产“玉兔”的固定成本为20000元,每生产一件“玉兔”需要增加投入100元,根据初步测算,总收益(单位:元)满足分段函数,其中是“玉兔”的月产量(单位:件),总收益=成本+利润
(1)试将利润元表示为月产量的函数;
(2)当月产量为多少件时利润最大?最大利润是多少?
【答案】(1) ;(2)当时,有最大利润25000元.
试题解析: (1)依题设,总成本为,
则
(2)当时,, 则当时,;
当时,是减函数,则,
所以,当时,有最大利润元.
20.(本小题12分)证券交易所规定,股票交易价格每日的涨跌幅均不得超过前一日收盘价的10%,当日涨幅达到10%称为涨停,跌幅达到10%称为跌停。
(1)、某投资人购买的股票先经历了一个涨停,又经历了一个跌停,分析该投资人赢亏情况;
(2)、如果他希望自己的股票在资金上翻番,至少要等多少个交易日以后? (lg1.1=0.0414,lg2=0.3010)
【答案】(1)(2) 3
试题解析:(1)、设投资人购买的股票价格为m,经历一个涨停后价格为m(1+10%)=1.1m,又经历一个跌停后价格为1.1m(1-10%)=0.99m所以投资人有一定的亏损。
(2)、设至少要n个交易日以后资金才会翻番且投资人的资金为a,
则: , 即:
两边取常用对数得:又lg1.1>0
故至少要8个交易日以后,资金才会翻番。
21. (本小题12分)某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分, 先收取固定的制版费,再按印刷数量收取印刷费;乙厂直接按印刷数量收取印刷费.甲厂的总费用y1(干元)、乙厂的总费用y2(千元)与印制证书数量 x(千个)的函数关系图分别如图中甲、乙所示.
(l)甲厂的制版费为____千元,印刷费为平均每个 元,甲厂的费用yl与证书数量x之间的函数关系为 ,
(2)当印制证书数量不超过2千个时,乙厂的印刷费为平均每个____ 元;
(3)当印制证书数量超过2干个时,求乙厂的总费用与证书数量x之间的函数关系式为 ;
(4)若该单位需印制证书数量为8干个,该单位应选择哪个厂更节省费用?请说明理由
【答案】(1)1;0.5;y=0.5x+1(2)1.5(3)(4) 选择乙厂更节省费用
试题解析:(1)印刷量为0时费用为1千元,因此制版费为1千元;图像过点,所以印刷2千时,费用为1千,因此平均费用为0.5;由函数过点,因此方程为y=0.5x+1;
(2)印刷量为2千时费用为3千,因此平均费用为1.5
(3)设y2=kx+b,
由图可知,当x=6时,y2=y1=0.5×6+1=4,
所以函数图象经过点(2,3)和(6,4)
所以把(2,3)和(6,4)代入y2=kx+b,得,
解得,所以y2与x之间的函数关系式为 .
(4)由图象可知,当x=8时,y1>y2,因此该单位选择乙厂更节省费用.
(求出当x=8时,y1和y2的值,用比较大小的方法得到结论也正确)
22. (本小题12分)根据市场调查,某种新产品投放市场的30天内,每件的销售价格(千元)与时间(天)组成有序数对,点落在下图中的两条线段上,且日销售量(件)与时间 (天)之间的关系是.
(Ⅰ) 写出该产品每件销售价格〔千元)与时间 (天)之间的函数关系式;
(Ⅱ) 在这30天内,哪一天的日销售金额最大?
(日销售金额每件产品的销售价格日销售量)
【答案】(Ⅰ);(Ⅱ)第10天的日销售金额最大.
试题解析:(Ⅰ)根据图象,每件的销售价格与时间的函数关系为:
(Ⅱ)设第天的日销售金额为(千元),则
即
当时,,
当时,,
当时,是减函数,
,
因此,这种产品在第10天的日销售金额最大.
1.四位好朋友在一次聚会上,他们按照各自的爱好选择了形状不同、内容高度相等、杯口半径相等的圆口酒杯,如下图所示,盛满酒后他们约定:先各自饮杯中酒的一半,设剩余酒的高度从左到右依次为,则它们的大小关系正确的是( )
A. B. C. D.
【答案】A
【解析】观察图形可知体积减少一半后剩余酒的高度最高为,最低为,故选A.
2.某商店按每件80元的价格购进某种时装1000件,根据市场预测,当每件售价100元时,可全售完;定价每提高1元,销售量就减少5件,若要获得最大利润,则售价应定为( )
A.110元 B.130元 C.150元 D.190元
【答案】C
3. 研究表明,当死亡生物组织内的碳14的含量不足死亡前的千分之一时,用一般的放射性探测器就测不到碳14了.若某一死亡生物组织内的碳14经过个“半衰期”后用一般的放射性探测器测不到碳14了,则的最小值是( )
(A)9 (B)10 (C)11 (D)12
【答案】B
【解析】由题可得函数关系式:,测.不到碳14了需小于千分之一时,
则当n=10时, 。
4.某公司为激励创新,计划逐年加大研发资金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是(参考数据:lg1.12≈0.05,lg1.3≈0.11,lg2≈0.30)( )
(A)2018年 (B)2019年 (C)2020年 (D)2021年
【答案】B
5.如图,有一直角墙角,两边的长度足够长,若处有一棵树与两墙的距离分别是和 (),不考虑树的粗细.现用长的篱笆,借助墙角围成一个矩形花圃,设此矩形花圃的最大面积为,若将这棵树围在矩形花圃内,则函数(单位: )的图象大致是( )
【答案】B
【解析】设长为,则长为 又因为要将点围在矩形内, ∴ 则矩形的面积为 当时,当且仅当时, 当时, ,
,
分段画出函数图形可得其形状与C接近 故选C.
6. 下图是抛物线形拱桥,当水面在时,拱顶离水面2米,水面宽4米,若水面下降0.42米后,则水面宽为( )
(A)2.2米 (B)4.4米 (C)2.4米 (D)4米
【答案】B
7.如图, 有四个平面图形分别是三角形、平行四边形、直角梯形、圆,垂直于轴的直线经过原点向右平行移动, 在移动过程中扫过平面图形的面积为(图中阴影部分), 若函数 的大致图象如图, 那么平面图形的形状不可能是( )
【答案】C
【解析】
试题分析:由函数图象可知,阴影部分的面积随的增大而增大,图象都是曲线,故选项A、B、D符合函数的图象,而C中刚开始的图象符合,到到梯形上底边时图象符合一次函数的图象,故选C.
8.根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为(A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是( )
A.75,25 B.75,16 C.60,25 D.60,16
【答案】D
9.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选1名代表,那么各班可推选人数与该班人数之间的函数关系用取整函数(表示不大于的最大整数)可以表示为( )
A. B.
C. D.
【答案】B
【解析】根据规定每人推选一名代表,当各班人数除以的余数大于时增加一名代表,即余数分别为时可以增选一名代表,也就是要进一位,所以最小应该加,因此利用取整函数可表示为,也可以用特殊取值法,若,排除C,D,若,排除A,故选B.
10.将甲桶中的升水缓慢注入空桶乙中,后甲桶剩余的水量符合指数衰减曲线.假设过后甲桶和乙桶的水量相等,若再过甲桶中的水只有升,则的值为( )
A.5 B.8
C.8 D.10
【答案】A
11. 出租车按如下方法收费:起步价7元,可行3(不含3);3到7(不含7)按元/计价(不足1按1计算);7以后按元/计价,到目的地结算时还需付1元的燃油附加费.若从甲地坐出租车到乙地(路程),需付车费(精确到1元) ( )
A、28元 B、27元 C、26元 D、25元
【答案】C
【解析】因为根据已知条件可知费用满足分段函数,所以需付车费
12. 衣柜里的樟脑丸,随着时间会挥发而体积缩小,刚放进的新丸体积为,经过天后体积与天数的关系式为:,若新丸经过50天后,体积变为;若一个新丸体积变为,则需经过的天数为
A.75天 B.100天 C.125天 D.150天
【答案】A.
【解析】由题意,得,解得;令,即,
即需经过的天数为75天.
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.抽气机每次抽出容器内空气的50%,则至少要抽__________次才能使容器内剩下的空气少于原来的0.1%.(参考数据:,)
【答案】
【解析】
设至少抽次,则由题意 即:,
两边取对数得,,即 ,
∴即至少要抽次.
14. 把物体放在冷空气中冷却,如果物体原来的温度是,空气的温度是,后物体的温度可由公式求得.把温度是的物体,放在的空气中冷却后,物体的温度是,那么的值约等于 .(保留三位有效数字,参考数据:取,取)
【答案】
【解析】依题意将代入公式可得,解得,.
15.某电脑公司2015年的各项经营收入中,经营电脑配件的收入为400万元,占全年经营总收入的40%.该公司预计2017年经营总收入要达到1 690万元,且计划从2015年到2017年,每年经营总收入的年增长率相同,2016年预计经营总收入为________万元.
【答案】1300
16.如图所示是某受污染的湖泊在自然净化过程中某种有害物质的剩留量y与净化时间t(月)的近似函数关系:y=at(t≥0,a>0且a≠1)的图象.有以下叙述:
①第4个月时,剩留量就会低于;
②每月减少的有害物质量都相等;
③若剩留量为, , 时,所经过的时间分别是t1,t2,t3,则t1+t2=t3.
其中所有正确叙述的序号是________.
【答案】①③
答案:①③.
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题10分)某食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)满足函数关系(e=2.718…为自然对数的底数,k,b为常数).若该食品在0℃的保鲜时间为192小时,在22℃的保鲜时间是48小时,求该食品在33℃的保鲜时间.
【答案】24小时.
【解析】
试题分析:由已知中保鲜时间与储藏温度是一种指数型关系,由已知构造方程组,
解得:;当时,运用指数幂的运算性质求解即可.
试题解析:由题意知,
,
.
所以当时,.
答:该食品在33℃的保鲜时间为24小时.
18.(本小题12分)某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在如下图象中的两条线段上.该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示:
(1)根据提供的图象,写出该种股票每股的交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少?
【答案】(1) (2) (3) 在30天中的第15天,日交易额的最大值为125万元
试题解析:(1)由图像知,前20天满足的是递增的直线方程,且过两点(0,2),(20,6),容易求得;从20天到30天满足递减的直线方程,且过两点(20,6),(30,5),求得方程为,
故P(元)与时间t(天)所满足的函数关系式为:
。。。。。。。。。。。。。。。4分
(2)由图表,易知Q与t满足一次函数关系,
即. ................7分
(3)由(1)(2)可知
.........................9分
当,t=15时,. .......................10分
当时,y随t的增大而减小. .........................11分
所以,在30天中的第15天,日交易额的最大值为125万元. .......12分
19.(本小题12分)某厂借嫦娥奔月的东风,推出品牌为“玉兔”的新产品,生产“玉兔”的固定成本为20000元,每生产一件“玉兔”需要增加投入100元,根据初步测算,总收益(单位:元)满足分段函数,其中是“玉兔”的月产量(单位:件),总收益=成本+利润
(1)试将利润元表示为月产量的函数;
(2)当月产量为多少件时利润最大?最大利润是多少?
【答案】(1) ;(2)当时,有最大利润25000元.
试题解析: (1)依题设,总成本为,
则
(2)当时,, 则当时,;
当时,是减函数,则,
所以,当时,有最大利润元.
20.(本小题12分)证券交易所规定,股票交易价格每日的涨跌幅均不得超过前一日收盘价的10%,当日涨幅达到10%称为涨停,跌幅达到10%称为跌停。
(1)、某投资人购买的股票先经历了一个涨停,又经历了一个跌停,分析该投资人赢亏情况;
(2)、如果他希望自己的股票在资金上翻番,至少要等多少个交易日以后? (lg1.1=0.0414,lg2=0.3010)
【答案】(1)(2) 3
试题解析:(1)、设投资人购买的股票价格为m,经历一个涨停后价格为m(1+10%)=1.1m,又经历一个跌停后价格为1.1m(1-10%)=0.99m
(2)、设至少要n个交易日以后资金才会翻番且投资人的资金为a,
则: , 即:
两边取常用对数得:又lg1.1>0
故至少要8个交易日以后,资金才会翻番。
21. (本小题12分)某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分, 先收取固定的制版费,再按印刷数量收取印刷费;乙厂直接按印刷数量收取印刷费.甲厂的总费用y1(干元)、乙厂的总费用y2(千元)与印制证书数量 x(千个)的函数关系图分别如图中甲、乙所示.
(l)甲厂的制版费为____千元,印刷费为平均每个 元,甲厂的费用yl与证书数量x之间的函数关系为 ,
(2)当印制证书数量不超过2千个时,乙厂的印刷费为平均每个____ 元;
(3)当印制证书数量超过2干个时,求乙厂的总费用与证书数量x之间的函数关系式为 ;
(4)若该单位需印制证书数量为8干个,该单位应选择哪个厂更节省费用?请说明理由
【答案】(1)1;0.5;y=0.5x+1(2)1.5(3)(4) 选择乙厂更节省费用
试题解析:(1)印刷量为0时费用为1千元,因此制版费为1千元;图像过点,所以印刷2千时,费用为1千,因此平均费用为0.5;由函数过点,因此方程为y=0.5x+1;
(2)印刷量为2千时费用为3千,因此平均费用为1.5
(3)设y2=kx+b,
由图可知,当x=6时,y2=y1=0.5×6+1=4,
所以函数图象经过点(2,3)和(6,4)
所以把(2,3)和(6,4)代入y2=kx+b,得,
解得,所以y2与x之间的函数关系式为 .
(4)由图象可知,当x=8时,y1>y2,因此该单位选择乙厂更节省费用.
(求出当x=8时,y1和y2的值,用比较大小的方法得到结论也正确)
22. (本小题12分)根据市场调查,某种新产品投放市场的30天内,每件的销售价格(千元)与时间(天)组成有序数对,点落在下图中的两条线段上,且日销售量(件)与时间 (天)之间的关系是.
(Ⅰ) 写出该产品每件销售价格〔千元)与时间 (天)之间的函数关系式;
(Ⅱ) 在这30天内,哪一天的日销售金额最大?
(日销售金额每件产品的销售价格日销售量)
【答案】(Ⅰ);(Ⅱ)第10天的日销售金额最大.
试题解析:(Ⅰ)根据图象,每件的销售价格与时间的函数关系为:
(Ⅱ)设第天的日销售金额为(千元),则
即
当时,,
当时,,
当时,是减函数,
,
因此,这种产品在第10天的日销售金额最大.
