高三物理动量、冲量和动量定理复习课件
图片预览











文档简介
课件43张PPT。动量、冲量和动量定理海安县立发中学杨本泉一、动量:P =m v 单位:kg.m/s 1、瞬时性:动量是指物体在某一时刻的动量,计算时应取这一时刻的瞬时速度。动量是描述物体运动状态的物理量,是状态量。2、矢量性:动量的方向与物体的瞬时速度方向相同。3、相对性:物体的动量与参照物的选择有关,选用不同的参照物时,同一物体的动量可能不同二、动量的变化:(1)、当物体的运动状态由状态1变化到状态2,其末动量mv2与初动量mv1的矢量差称为动量的变化,即?P= mv2 - mv1,或?P=P2-P1(2)、动量变化的矢量性:由于动量是矢量,所以动量的变化也是矢量。(3)、动量变化的计算:运算应用平行四边形定则。如果在同一方向上选定正方向后,可用“+”“-”表示方向。例1。两小球的质量分别是m1和m2,且m1=2m2,当它们的动能相等时,它们的动量大小之比是 .例2。质量为10Kg的物体,当其速率由
3m/s变为4m/s时,它的动量变化量Δp
的大小不可能的是……( )
A、10kgm/s B、50kgm/s
C、70kgm/s D、90kgm/sD三、冲量(力对时间的累积效应) I=Ft 单位:N?s注:冲量大小不仅与力有关,还与力的作用时间有关。变力的冲量一般不能用I=Ft 来计算,而应根据动量定理,用动量的改变量等效代换。1.矢量性:恒力(或方向不变的力),冲量方向与力的方向一致;变力(方向改变的力),冲量方向应与物体动量改变量的方向一致。2.过程量:它是力对物体的作用经历一段时间的积累效应。与位移无关。理
解3.绝对性:力与时间与参照系的选取无关,冲量的大小、方向与参照系的选取无关。例3.质量为m的物体放在水平地面上,在与水平面成?角的拉力F作用下由静止开始运动,经时间t速度达到v,在这段时间内拉力F和重力mg冲量大小分别是(D)
A.Ft,0
B.Ftcos?,0
C.mv,0
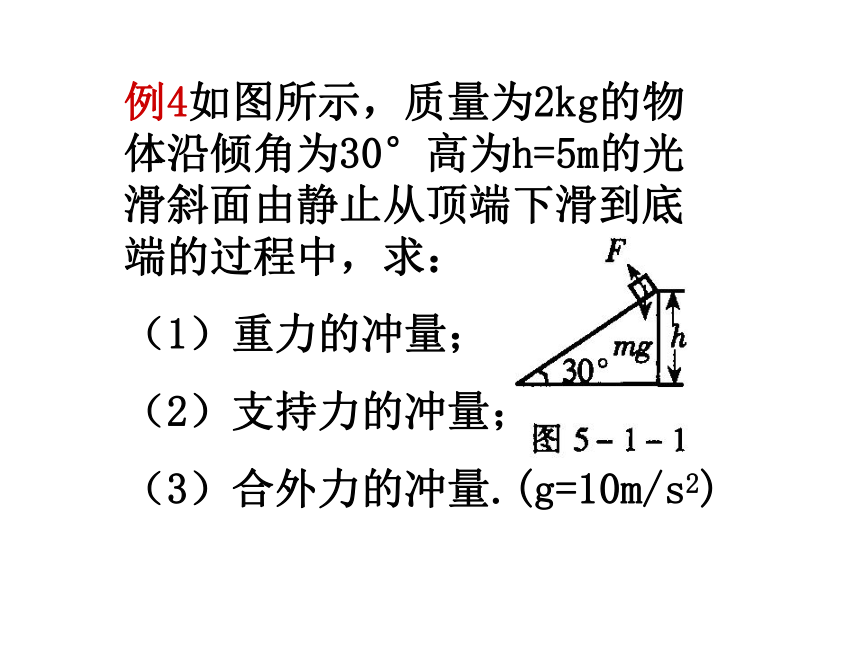
D.Ft,mgt例4如图所示,质量为2kg的物体沿倾角为30°高为h=5m的光滑斜面由静止从顶端下滑到底端的过程中,求:
(1)重力的冲量;
(2)支持力的冲量;
(3)合外力的冲量.(g=10m/s2)【解析】求某个力的冲量时,只有恒力才能用公式I=F·t,而对于变力一般用动量定理求解,此题物体下滑过程中各力均为恒力,所以只要求出力作用时间便可用I=Ft求解.
由牛顿第二定律F=ma得
下滑的加速度a=g·sin?=5m/s2.由s=(1/2)at2得下滑时间,
所以重力的冲量IG=mg·t=2×10×2=40N·s.
支持力的冲量IF=F·t=mgcos30°·t=20 N·s,
合外力的冲量IF合=F合·t=mgsin30°·t=20N·s.【解题回顾】某个力的冲量与合外力的冲量要注意区分.如5-1-2图,物重10N,放在桌面上静止不动,经历时间10秒钟,重力的冲量不是0而是IG=G·t=10×10=100N·s.四、动量定理(矢量式) 物体所受合外力的冲量等于它的动量的变化。
或 物体所受各个力的冲量之和等于它的动量的变化。
I合=?p=p2-p1或 F·?t=mv2-mv1理解:有一质量为5Kg的物体在高为70m的地方以5m/s的水平初速度抛出,求第3秒内物体动量变化的大小及方向?1、式中的“=”不仅表示大小相等,同时还表示方向相同。2、因果关系:合力的冲量是动量变化的原因3、过程方程:与牛顿第二定律的瞬时性不同,力在瞬间可产生加速度,但不能改变动量,只有在一段时间才能改变物体的动量。4、研究对象。高中阶段只要求研究单个质点,事实上也 适用于一个系统。质量为m的物体,沿半径为R的轨道以速率υ做匀速圆周运动,求物体所受的合外力在半个周期内的冲量?5、适用范围。不论恒力还是变力,不论轨迹是直线还是曲线,不论运动时间的长短,动量定理都适用。6、动量定理中的冲量可以是恒力的冲量也可以是变力的冲理,因此利用动量定理可以求变力的冲量。7、由动量定理得:F合=(P2-P1)/t即物体动量的变化率等于它受到的合外力。8、动量定理只适用于惯性参照系,通常选地面为参照系。例5、关于冲量、动量及动量变化,下列说法正确的是: ( )
A. 冲量方向一定和动量变化的方向相同
B. 冲量的大小一定和动量变化的大小相同
C. 动量的方向改变,冲量方向一定改变
D. 动量的大小不变,冲量一定为0.A B练习。在空间某一点以大小相同的速度分别竖直上抛、竖直下抛、水平抛出质量相等的小球,若空气阻力不计,经过t秒:(假设小球均未落地)( ) (A)作上抛运动的小球动量变化最小 (B)作下抛运动的小球动量变化最大 (C)作平抛运动小球动量变化最小 (D)三小球动量变化相等D练习、质量为1kg的物体做变速直线运动,它的速度时间图象如图所示,则该物体在前10s内与后10s内两段时间,所受合外力的冲量分别是……( )
A、10N?s,10N ? s B、10N ? s,-10N ? s
C、0, 10N ? s D、 0, - 10N ? s D练习.以速度υ0竖直上抛一个质量为m的物体,不计阻力,物体在运动过程中(取竖直向上为正)。
(1)动量增量△P随时间t变化的图线是图中的哪一个? A B C DC(2)若纵轴表示动量的变化率,则动量变化率随时间t的变化图线是图中的哪一个?(取竖直向上为正)( )t△P/t0tt△P/t0t△P/t0 A B C DD(3)从抛出到物体回到原点的整个过程中所受到的总冲量为 ,平均作用力大小为 。物体在上升阶段受到的总冲量为 ,下落阶段受到的总冲量为 。-2mv0mg-mv0-mv0(4)若小球运动时受空气阻力且大小不变则
A、从抛出到落回原处的时间内,重力的冲量为零
B、上升时空气阻力的冲量小于下落时空气阻力的冲量
C、从抛出到落回原处的时间内,空气阻力的冲量为零
D、上升阶段小球的动量变化大于下落阶段小球的动量变化B、D 在光滑水平面上水平固定放置一端固定的轻质弹簧,质量为 m 的小球沿弹簧所位于的直线方向以速度V运动,并和弹簧发生碰撞,小球和弹簧作用后又以相同的速度反弹回去。在球和弹簧相互作用过程中,弹簧对小球的冲量I 的大小和弹簧对小球所做的功W分别为( )
(A) I=0、 W=mv2
(B) I=2mv、W = 0
(C) I=mv、 W = mv2/2
(D) I=2mv、W = mv2/2B例6五、用动量定理解题的一般步骤 1、确定研究对象; 2、确定所研究的物理过程及始末状态的动量; 3、分析研究对象在所研究的物理过程中的受力情况,画受力图; 4、规定正方向,用动量定理列式; 5、公式变形,统一单位,代数据求解;必要时对结果进行讨论。判断1:质量为50kg 的工人,身上系着长为5m的弹性安全带在高空作业,不慎掉下,若从弹性绳开始伸直到工人落到最低点经历的时间为0.5s,求弹性绳对工人的平均作用力。(g = 10m/s2)判断2:质量为50kg 的工人,身上系着长为5m的弹性安全带在高空作业,不慎掉下,若从弹性绳开始伸直到工人落到最低点弹性绳伸长了2m,求弹性绳对工人的平均作用力。(g = 10m/s2) 小结:在题中涉及到的物理量主要是F、t、m、v 时,考虑用动量定理求解。 小结:在题中涉及到的物理量主要是F、s、m、v 时,考虑用动能定理求解。一、明确什么类型的题目
用动量定理解步骤简单练习:如图所示,物体质量为m,初速度为v,冲上倾角为θ 的固定斜面,物体与斜面之间的动摩擦因数为μ ,求物体冲到最高点所用的时间。解法一:用牛顿运动定律知识解解得 t=v/(gsin θ + μ gcos θ )解法二:用动量定理解F合= mg sinθ + μ mgcos θ-F合t=0-mv 规定沿斜面向上为正方向解得 t=v/(gsin θ + μ gcos θ )用任何一种方法,只要解出来就是高手!但考试时你会如何选择?
物体A和B用轻绳相连挂在轻弹簧下静止不动,如图(a)所示。A的质量为m,B的质量为M,将连接A、B的绳烧断后,物体A上升经某一位置时的速度大小为v,这时物体B的下落速度大小为u,如图(b)所示,在这段时间里,弹簧弹力对物体A的冲量等于( )(A)mv (B)mv-Mu
(C)mv+Mu (D)mv+mu解:对B物,由动量定理Mgt=Mu∴ gt=u对A物,由动量定理IF – mgt = mv∴ IF =mgt + mv = mu + mvD 例7(二)动量定理的应用1、用动量定理解释一些现象(一)、用动量定理解释现象 例8:人从高处跳下,与地面接触时双腿弯曲,这样是为了( )
A、减少落地时的动量 B、减少动量的变化
C、减少冲量 D、减小地面对人的冲力 1、物体的动量的变化一定,此时力的作用时间越短,力就越大;力的作用时间越长,力就越小。D 2、作用力一定,力的作用时间越长,动量变化就越大;力的作用时间越短,动量变化就越小。 例9:把重物压在纸带上,用一水平力缓缓拉动纸带,重物跟着纸带一起运动;若迅速拉动纸带,纸带就会从重物下抽出,解释这个现象的原因是( )
A、在缓缓拉动纸带时,纸带给重物的摩擦力大
B、在迅速拉动纸带时,纸带给重物的摩擦力大
C、在缓缓拉动纸带时,纸带给重物的冲量大
D、在迅速拉动纸带时,纸带给重物的冲量大C能力·思维·方法【解析】在缓缓拉动时,两物体之间的作用力是静摩擦力;在迅速拉动时,它们之间的作用力是滑动摩擦力.由于滑动摩擦力f=μN(μ是动摩擦因数),而最大静摩擦力fm=μmN(μm是静摩擦系数)且μ= μm.一般情况下可以认为f=fm即滑动摩擦力f近似等于最大静摩擦力fm.因此,一般情况是:缓拉,摩擦力小;快拉,摩擦力大,故判断A、B都错.能力·思维·方法 缓拉纸带时,摩擦力虽小些,但作用时间可以很长,故重物获得的冲量,即动量的改变量可以很大,所以能把重物带动;快拉时,摩擦力虽大些,但作用时间很短,故冲量小,所以重物动量的改变量小.因此答案C、D正确.【例10】某消防队员质量60Kg从一平台上跳下,下落2m后双脚触地,接着他用双腿弯曲的方法缓冲,使自身重心又下降了0.5s.在着地过程中,对他双脚的平均作用力估计为 能力·思维·方法△t= △h/v平均=△h/(v/2)=2△h/v.
在触地过程中,有(N-mg)△t=m△v,
即N=mg+m△v/△t=mg+mv/(2△h/v)
=mg+mv2/2h,
=mg+mgh/△h=5mg.
因此答案B正确.能力·思维·方法【解题回顾】题中的(N-mg)△t=m△v,许多同学在独立做题时容易做成N△t=m△v而得出N=4mg的错误结论.2、曲线运动中动量的变化和冲量
(二)、曲线运动中动量的变化和冲量 例11:质量为m 的物体作平抛运动,求抛出后第2个t 秒内物体动量的变化。 分析:由动量定理,Δp = I合= mg t ,方向竖直向下。 例12:质量为m 的小球用长为L 的细线挂在O 点,将小球向右拉开,使细线与竖直方向成θ角后无初速释放,已知小球运动到最低点所需的时间为t,求这个过程中重力和合力的冲量。 分析: IG= mg t ,方向竖直向下;由动量定理, I合=Δp = mv - 0由机械能守恒可得:v =[ 2gL(1 - cos θ)]1/2方向水平向左。则 I合= m [ 2gL(1 - cos θ)]1/2,拉力的冲量呢?例13 一质点在水平面内以速度v做匀速圆周运动,如图,质点从位置A开始,经1/2圆周,质点所受合力的冲量是多少? 解:?质点做匀速圆周运动,合力是一个大小不变、但方向不断变化的力,注意:?变力的冲量一般不能直接由F·Δt求出,可借助ΣF·Δt=Δp间接求出,即合外力力的冲量由末动量与初动量的矢量差来决定. 以vB方向为正,因为vA =- v , vB = v ,则Δp=mvB - mvA =m[v - ( - v )]=2mv,合力冲量与vB同向.(三)、用动量定理解决变质量问题思考:宇宙飞船以v的速度在宇宙空间运动,飞船的横截面积为s,当进入有宇宙尘埃的区域时,每立方米中有n个小颗粒,每个小颗粒的质量为m,如小颗粒碰到飞船时可认为是静止的,且碰上就粘在飞船上,为保持匀速运动,飞船发动机的牵引力大小为多少?练习.高压采煤水枪出水口的截面积为S,水的射速为υ,射到煤层上后,水速度为零,若水的密度为ρ,求水对煤层的冲力。 一质量为m的小球,以初速度v0 沿水平方向射出,恰好垂直地射到一倾角为30° 的固定斜面上,并立即反方向弹回。已知反弹速度的大小是入射速度大小的3/4,求在碰撞中斜面对小球的冲量大小思维训练 1。04年广东解:小球在碰撞斜面前做平抛运动.设刚要碰撞斜面时小球速度为v. 由题意,v 的方向与竖直线的夹角为30°,且水平分量仍为v0,如右图. 由此得 v = 2v0 ① 碰撞过程中,小球速度由v变为反向的3v/4,
碰撞时间极短,可不计重力的冲量,由动量定理,斜面对小球的冲量为由①、②得 思维训练 2(02年26题)(20分)蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目。一个质量为60kg的运动员,从离水平网面3.2m高处自由下落,着网后沿竖直方向蹦回到离水平网面5.0m高处。已知运动员与网接触的时间为1.2s。若把在这段时间内网对运动员的作用力当作恒力处理,求此力的大小。(g=10m/s2) 质量为m1的气球下端用细绳吊一质量为m2 的物体,由某一高处从静止开始以加速度a下降,经时间t1绳断开,气球与物体分开,再经时间t2气球速度为零(不计空气阻力),求此时物体m2的速度是多大? 思维训练3解:?画出运动过程示意图:本题可用牛顿第二定律求解,但过程繁琐,用动量定理可使解题过程大大简化.以(m1 +m2 )物体系为研究对象,分析受力,细绳断开前后整体所受合外力为:ΣF=(m1 +m2 )a 一直不变,对系统(m1 +m2 )用动量定理: (m1+m2 )a t1+(m1+m2 )a t2 =m2v′- 0得?v′=(m1+m2 )(t1+t2 )a /m2 方向竖直向下.思维训练 4***长为L的轻绳一端系
于固定点O,另一端系质
量为m的小球,将小球从
O点正下方L/4处,以一定
初速度水平向右抛出,经一定时间绳被拉直以后,小球将以O为支点在竖直平面内摆动,已知绳刚被拉直时绳与竖直线成600角,如图所示,求:
(1)小球水平抛出时的初速度υ0
(2)在绳拉紧的瞬间,支点O受到的冲量I;
(3)小球摆到最低点时,绳所受拉力T。***思维训练 5: 据报载:1962年,一架“子爵号”客机,在美国的伊利奥特市上空与一只天鹅相撞,客机坠毁,十七人丧生.1980年,一架英国的“鸽式”战斗机在威夫士地区上空与一只秃鹰相撞,飞机坠毁,飞行员弹射逃生.
小小的飞禽何以能撞毁飞机这样的庞然大物?下面我们通过简要计算来说明这一问题.
设:鸟的质量m=1.0kg,鸟的身长L=15cm,鸟与飞机相撞面积S=0.01,相撞前鸟的速度约为零(因远小于飞机速度),相撞后其速度与飞机相同,飞机飞行速度v=600m/s(现代超音速飞机的飞行速度是声速的二到三倍),因飞机质量M?m,故相撞过程中飞机速度不变。
3m/s变为4m/s时,它的动量变化量Δp
的大小不可能的是……( )
A、10kgm/s B、50kgm/s
C、70kgm/s D、90kgm/sD三、冲量(力对时间的累积效应) I=Ft 单位:N?s注:冲量大小不仅与力有关,还与力的作用时间有关。变力的冲量一般不能用I=Ft 来计算,而应根据动量定理,用动量的改变量等效代换。1.矢量性:恒力(或方向不变的力),冲量方向与力的方向一致;变力(方向改变的力),冲量方向应与物体动量改变量的方向一致。2.过程量:它是力对物体的作用经历一段时间的积累效应。与位移无关。理
解3.绝对性:力与时间与参照系的选取无关,冲量的大小、方向与参照系的选取无关。例3.质量为m的物体放在水平地面上,在与水平面成?角的拉力F作用下由静止开始运动,经时间t速度达到v,在这段时间内拉力F和重力mg冲量大小分别是(D)
A.Ft,0
B.Ftcos?,0
C.mv,0
D.Ft,mgt例4如图所示,质量为2kg的物体沿倾角为30°高为h=5m的光滑斜面由静止从顶端下滑到底端的过程中,求:
(1)重力的冲量;
(2)支持力的冲量;
(3)合外力的冲量.(g=10m/s2)【解析】求某个力的冲量时,只有恒力才能用公式I=F·t,而对于变力一般用动量定理求解,此题物体下滑过程中各力均为恒力,所以只要求出力作用时间便可用I=Ft求解.
由牛顿第二定律F=ma得
下滑的加速度a=g·sin?=5m/s2.由s=(1/2)at2得下滑时间,
所以重力的冲量IG=mg·t=2×10×2=40N·s.
支持力的冲量IF=F·t=mgcos30°·t=20 N·s,
合外力的冲量IF合=F合·t=mgsin30°·t=20N·s.【解题回顾】某个力的冲量与合外力的冲量要注意区分.如5-1-2图,物重10N,放在桌面上静止不动,经历时间10秒钟,重力的冲量不是0而是IG=G·t=10×10=100N·s.四、动量定理(矢量式) 物体所受合外力的冲量等于它的动量的变化。
或 物体所受各个力的冲量之和等于它的动量的变化。
I合=?p=p2-p1或 F·?t=mv2-mv1理解:有一质量为5Kg的物体在高为70m的地方以5m/s的水平初速度抛出,求第3秒内物体动量变化的大小及方向?1、式中的“=”不仅表示大小相等,同时还表示方向相同。2、因果关系:合力的冲量是动量变化的原因3、过程方程:与牛顿第二定律的瞬时性不同,力在瞬间可产生加速度,但不能改变动量,只有在一段时间才能改变物体的动量。4、研究对象。高中阶段只要求研究单个质点,事实上也 适用于一个系统。质量为m的物体,沿半径为R的轨道以速率υ做匀速圆周运动,求物体所受的合外力在半个周期内的冲量?5、适用范围。不论恒力还是变力,不论轨迹是直线还是曲线,不论运动时间的长短,动量定理都适用。6、动量定理中的冲量可以是恒力的冲量也可以是变力的冲理,因此利用动量定理可以求变力的冲量。7、由动量定理得:F合=(P2-P1)/t即物体动量的变化率等于它受到的合外力。8、动量定理只适用于惯性参照系,通常选地面为参照系。例5、关于冲量、动量及动量变化,下列说法正确的是: ( )
A. 冲量方向一定和动量变化的方向相同
B. 冲量的大小一定和动量变化的大小相同
C. 动量的方向改变,冲量方向一定改变
D. 动量的大小不变,冲量一定为0.A B练习。在空间某一点以大小相同的速度分别竖直上抛、竖直下抛、水平抛出质量相等的小球,若空气阻力不计,经过t秒:(假设小球均未落地)( ) (A)作上抛运动的小球动量变化最小 (B)作下抛运动的小球动量变化最大 (C)作平抛运动小球动量变化最小 (D)三小球动量变化相等D练习、质量为1kg的物体做变速直线运动,它的速度时间图象如图所示,则该物体在前10s内与后10s内两段时间,所受合外力的冲量分别是……( )
A、10N?s,10N ? s B、10N ? s,-10N ? s
C、0, 10N ? s D、 0, - 10N ? s D练习.以速度υ0竖直上抛一个质量为m的物体,不计阻力,物体在运动过程中(取竖直向上为正)。
(1)动量增量△P随时间t变化的图线是图中的哪一个? A B C DC(2)若纵轴表示动量的变化率,则动量变化率随时间t的变化图线是图中的哪一个?(取竖直向上为正)( )t△P/t0tt△P/t0t△P/t0 A B C DD(3)从抛出到物体回到原点的整个过程中所受到的总冲量为 ,平均作用力大小为 。物体在上升阶段受到的总冲量为 ,下落阶段受到的总冲量为 。-2mv0mg-mv0-mv0(4)若小球运动时受空气阻力且大小不变则
A、从抛出到落回原处的时间内,重力的冲量为零
B、上升时空气阻力的冲量小于下落时空气阻力的冲量
C、从抛出到落回原处的时间内,空气阻力的冲量为零
D、上升阶段小球的动量变化大于下落阶段小球的动量变化B、D 在光滑水平面上水平固定放置一端固定的轻质弹簧,质量为 m 的小球沿弹簧所位于的直线方向以速度V运动,并和弹簧发生碰撞,小球和弹簧作用后又以相同的速度反弹回去。在球和弹簧相互作用过程中,弹簧对小球的冲量I 的大小和弹簧对小球所做的功W分别为( )
(A) I=0、 W=mv2
(B) I=2mv、W = 0
(C) I=mv、 W = mv2/2
(D) I=2mv、W = mv2/2B例6五、用动量定理解题的一般步骤 1、确定研究对象; 2、确定所研究的物理过程及始末状态的动量; 3、分析研究对象在所研究的物理过程中的受力情况,画受力图; 4、规定正方向,用动量定理列式; 5、公式变形,统一单位,代数据求解;必要时对结果进行讨论。判断1:质量为50kg 的工人,身上系着长为5m的弹性安全带在高空作业,不慎掉下,若从弹性绳开始伸直到工人落到最低点经历的时间为0.5s,求弹性绳对工人的平均作用力。(g = 10m/s2)判断2:质量为50kg 的工人,身上系着长为5m的弹性安全带在高空作业,不慎掉下,若从弹性绳开始伸直到工人落到最低点弹性绳伸长了2m,求弹性绳对工人的平均作用力。(g = 10m/s2) 小结:在题中涉及到的物理量主要是F、t、m、v 时,考虑用动量定理求解。 小结:在题中涉及到的物理量主要是F、s、m、v 时,考虑用动能定理求解。一、明确什么类型的题目
用动量定理解步骤简单练习:如图所示,物体质量为m,初速度为v,冲上倾角为θ 的固定斜面,物体与斜面之间的动摩擦因数为μ ,求物体冲到最高点所用的时间。解法一:用牛顿运动定律知识解解得 t=v/(gsin θ + μ gcos θ )解法二:用动量定理解F合= mg sinθ + μ mgcos θ-F合t=0-mv 规定沿斜面向上为正方向解得 t=v/(gsin θ + μ gcos θ )用任何一种方法,只要解出来就是高手!但考试时你会如何选择?
物体A和B用轻绳相连挂在轻弹簧下静止不动,如图(a)所示。A的质量为m,B的质量为M,将连接A、B的绳烧断后,物体A上升经某一位置时的速度大小为v,这时物体B的下落速度大小为u,如图(b)所示,在这段时间里,弹簧弹力对物体A的冲量等于( )(A)mv (B)mv-Mu
(C)mv+Mu (D)mv+mu解:对B物,由动量定理Mgt=Mu∴ gt=u对A物,由动量定理IF – mgt = mv∴ IF =mgt + mv = mu + mvD 例7(二)动量定理的应用1、用动量定理解释一些现象(一)、用动量定理解释现象 例8:人从高处跳下,与地面接触时双腿弯曲,这样是为了( )
A、减少落地时的动量 B、减少动量的变化
C、减少冲量 D、减小地面对人的冲力 1、物体的动量的变化一定,此时力的作用时间越短,力就越大;力的作用时间越长,力就越小。D 2、作用力一定,力的作用时间越长,动量变化就越大;力的作用时间越短,动量变化就越小。 例9:把重物压在纸带上,用一水平力缓缓拉动纸带,重物跟着纸带一起运动;若迅速拉动纸带,纸带就会从重物下抽出,解释这个现象的原因是( )
A、在缓缓拉动纸带时,纸带给重物的摩擦力大
B、在迅速拉动纸带时,纸带给重物的摩擦力大
C、在缓缓拉动纸带时,纸带给重物的冲量大
D、在迅速拉动纸带时,纸带给重物的冲量大C能力·思维·方法【解析】在缓缓拉动时,两物体之间的作用力是静摩擦力;在迅速拉动时,它们之间的作用力是滑动摩擦力.由于滑动摩擦力f=μN(μ是动摩擦因数),而最大静摩擦力fm=μmN(μm是静摩擦系数)且μ= μm.一般情况下可以认为f=fm即滑动摩擦力f近似等于最大静摩擦力fm.因此,一般情况是:缓拉,摩擦力小;快拉,摩擦力大,故判断A、B都错.能力·思维·方法 缓拉纸带时,摩擦力虽小些,但作用时间可以很长,故重物获得的冲量,即动量的改变量可以很大,所以能把重物带动;快拉时,摩擦力虽大些,但作用时间很短,故冲量小,所以重物动量的改变量小.因此答案C、D正确.【例10】某消防队员质量60Kg从一平台上跳下,下落2m后双脚触地,接着他用双腿弯曲的方法缓冲,使自身重心又下降了0.5s.在着地过程中,对他双脚的平均作用力估计为 能力·思维·方法△t= △h/v平均=△h/(v/2)=2△h/v.
在触地过程中,有(N-mg)△t=m△v,
即N=mg+m△v/△t=mg+mv/(2△h/v)
=mg+mv2/2h,
=mg+mgh/△h=5mg.
因此答案B正确.能力·思维·方法【解题回顾】题中的(N-mg)△t=m△v,许多同学在独立做题时容易做成N△t=m△v而得出N=4mg的错误结论.2、曲线运动中动量的变化和冲量
(二)、曲线运动中动量的变化和冲量 例11:质量为m 的物体作平抛运动,求抛出后第2个t 秒内物体动量的变化。 分析:由动量定理,Δp = I合= mg t ,方向竖直向下。 例12:质量为m 的小球用长为L 的细线挂在O 点,将小球向右拉开,使细线与竖直方向成θ角后无初速释放,已知小球运动到最低点所需的时间为t,求这个过程中重力和合力的冲量。 分析: IG= mg t ,方向竖直向下;由动量定理, I合=Δp = mv - 0由机械能守恒可得:v =[ 2gL(1 - cos θ)]1/2方向水平向左。则 I合= m [ 2gL(1 - cos θ)]1/2,拉力的冲量呢?例13 一质点在水平面内以速度v做匀速圆周运动,如图,质点从位置A开始,经1/2圆周,质点所受合力的冲量是多少? 解:?质点做匀速圆周运动,合力是一个大小不变、但方向不断变化的力,注意:?变力的冲量一般不能直接由F·Δt求出,可借助ΣF·Δt=Δp间接求出,即合外力力的冲量由末动量与初动量的矢量差来决定. 以vB方向为正,因为vA =- v , vB = v ,则Δp=mvB - mvA =m[v - ( - v )]=2mv,合力冲量与vB同向.(三)、用动量定理解决变质量问题思考:宇宙飞船以v的速度在宇宙空间运动,飞船的横截面积为s,当进入有宇宙尘埃的区域时,每立方米中有n个小颗粒,每个小颗粒的质量为m,如小颗粒碰到飞船时可认为是静止的,且碰上就粘在飞船上,为保持匀速运动,飞船发动机的牵引力大小为多少?练习.高压采煤水枪出水口的截面积为S,水的射速为υ,射到煤层上后,水速度为零,若水的密度为ρ,求水对煤层的冲力。 一质量为m的小球,以初速度v0 沿水平方向射出,恰好垂直地射到一倾角为30° 的固定斜面上,并立即反方向弹回。已知反弹速度的大小是入射速度大小的3/4,求在碰撞中斜面对小球的冲量大小思维训练 1。04年广东解:小球在碰撞斜面前做平抛运动.设刚要碰撞斜面时小球速度为v. 由题意,v 的方向与竖直线的夹角为30°,且水平分量仍为v0,如右图. 由此得 v = 2v0 ① 碰撞过程中,小球速度由v变为反向的3v/4,
碰撞时间极短,可不计重力的冲量,由动量定理,斜面对小球的冲量为由①、②得 思维训练 2(02年26题)(20分)蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目。一个质量为60kg的运动员,从离水平网面3.2m高处自由下落,着网后沿竖直方向蹦回到离水平网面5.0m高处。已知运动员与网接触的时间为1.2s。若把在这段时间内网对运动员的作用力当作恒力处理,求此力的大小。(g=10m/s2) 质量为m1的气球下端用细绳吊一质量为m2 的物体,由某一高处从静止开始以加速度a下降,经时间t1绳断开,气球与物体分开,再经时间t2气球速度为零(不计空气阻力),求此时物体m2的速度是多大? 思维训练3解:?画出运动过程示意图:本题可用牛顿第二定律求解,但过程繁琐,用动量定理可使解题过程大大简化.以(m1 +m2 )物体系为研究对象,分析受力,细绳断开前后整体所受合外力为:ΣF=(m1 +m2 )a 一直不变,对系统(m1 +m2 )用动量定理: (m1+m2 )a t1+(m1+m2 )a t2 =m2v′- 0得?v′=(m1+m2 )(t1+t2 )a /m2 方向竖直向下.思维训练 4***长为L的轻绳一端系
于固定点O,另一端系质
量为m的小球,将小球从
O点正下方L/4处,以一定
初速度水平向右抛出,经一定时间绳被拉直以后,小球将以O为支点在竖直平面内摆动,已知绳刚被拉直时绳与竖直线成600角,如图所示,求:
(1)小球水平抛出时的初速度υ0
(2)在绳拉紧的瞬间,支点O受到的冲量I;
(3)小球摆到最低点时,绳所受拉力T。***思维训练 5: 据报载:1962年,一架“子爵号”客机,在美国的伊利奥特市上空与一只天鹅相撞,客机坠毁,十七人丧生.1980年,一架英国的“鸽式”战斗机在威夫士地区上空与一只秃鹰相撞,飞机坠毁,飞行员弹射逃生.
小小的飞禽何以能撞毁飞机这样的庞然大物?下面我们通过简要计算来说明这一问题.
设:鸟的质量m=1.0kg,鸟的身长L=15cm,鸟与飞机相撞面积S=0.01,相撞前鸟的速度约为零(因远小于飞机速度),相撞后其速度与飞机相同,飞机飞行速度v=600m/s(现代超音速飞机的飞行速度是声速的二到三倍),因飞机质量M?m,故相撞过程中飞机速度不变。
