万有引力理论的成就
图片预览










文档简介
课件39张PPT。万有引力理论的成就请同学们粗略的来计算一下两个质量为50kg,相距0.5m的人之间的引力?思考:为什么说是忽略?
◆ 那么太阳与地球之间的万有引力又是多大呢?已知:太阳的质量为M=2.0×1030kg,地球质量为m=6.0×1024kg,日地之间的距离为R=1.5×1011kmF=GMm/R23.5×1022N非常大,能够拉断直径为9000km的钢柱。=3.5×1022(N)而太阳对质量为50kg的人,引力很小,不到0.3N。
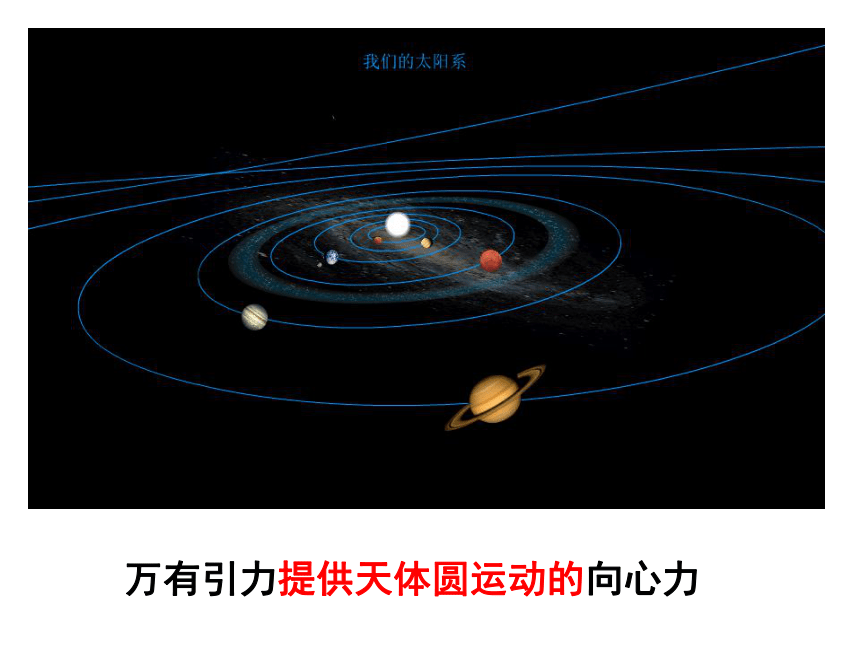
当然我们感受不到太阳的引力。=6.67×10-11×2.0×1030×6.0×1024/(1.5×1011)2 万有引力支配天体的运动 万有引力理论的成就万有引力提供天体圆运动的向心力万有引力定律对物理学、天文学的发展具有深远的影响;它把地面上物体运动的规律和天体运动的规律统一起来;对科学文化发展起到了积极的推动作用,解放了人们的思想,给人们探索自然的奥秘建立了极大信心,使人们有能力理解天地间的各种事物。时至今日,数千颗人造卫星正在按照万有引力定律为它们设定的轨道绕地球运转着。所以没有万有引力定律,就没有今天的天空漫步,当然也没有卫星通信时代了。以至于阿波罗8号从月球返航的途中,当地面控制中心问及“是谁在驾驶”的时候,指令长这样回答:“我想现在是牛顿在驾驶。”思考一:万有引力在天文学上有哪些方面的应用呢?“科学真是迷人”-测地球的质量问题一:如何测地球的质量? 天平能用吗?
问题一:如果要知道地球的质量,应该知道哪些条件?
当时已知:
地表重力加速度:g = 9.8m/s2
地球半径: R = 6400km
引力常量: G=6.67×10-11Nm2/kg2
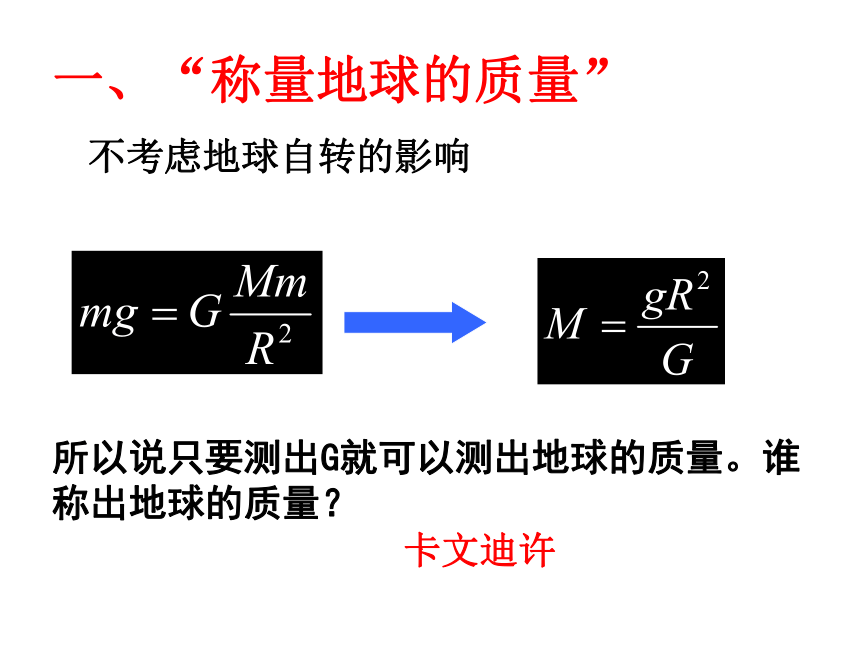
一、“称量地球的质量”不考虑地球自转的影响所以说只要测出G就可以测出地球的质量。谁称出地球的质量?卡文迪许把数据代入具体算一下地球质量:地表重力加速度:g = 9.8m/s2
地球半径: R = 6400km
引力常量: G=6.67×10-11Nm2/kg2=6.0x1024kg思考:用同样的方法如何来测其它天体的质量呢?小结:求天体质量方法一:不考虑天体自转的影响:已知:三个量g、R、G三个量就可以求 一宇航员为了估测一星球的质量,他在该星球的表面做自由落体实验:让小球在离地面h高处自由下落,他测出经时间t小球落地,又已知该星球的半径为R,试估算该星球的质量。2hR2/Gt2练习一:思考二:如何才能知道太阳的质量呢?上面的方法可行吗?
能不能借用行星来称量呢?
请同学们看书后回答二、计算太阳的质量 我们可以测出太阳某行星的公转周期T、轨道半径r,能不能由此求出太阳的质量M?分析:
1.将行星的运动看成是匀速圆周运动.
2.万有引力充当向心力 F引=Fn.
只可求出中心天体的质量,
求不出环绕天体的质量。求天体质量方法二: 计算中心天体的质量情景: m(环绕天体)绕着M(中心天体)转,测出m运动周期T和离中心天体M的轨道半径r就可求出中心天体M: F引=Fn练习二:用上面方法如何求地球质量呢?已知 地球半径: R = 6400×103m
月亮周期: T = 27.3天≈2.36×106s
月亮轨道半径: r ≈ 60R,
求 地球的质量M? F引=Fn思考:如果不知道环绕天体的周期而是知道它的线速度或角速度,可以求中心天体质量吗?总结: 应用万有引力定律可以计算天体的质量:
(1)M=v2r/G.
(2)M=ω2r3/G.
(3)M=4π2r3/GT2.
(4) M=gR2/G.
ρ三、计算天体的密度 若环绕天体m接近中心天体M表面飞行则密度多少?r=R练习三;一艘宇宙飞船飞近一个不知名的行星,并进入靠近该行星表面的圆形轨道,宇航员进入预定的考察工作,宇航员能不能仅用一只表通过测定时间来测定该行星的密度?说明理由及推导过程四、发现未知天体背景:
1781年由英国物理学家威廉.赫歇尔发现了天王星,但人们观测到的天王星的运行轨迹与万有引力定律推测的结果有一些误差…… 天王星的运行轨道有些古怪 四、发现未知天体四、发现未知天体1:1845年英国人亚当斯和法国天文学家勒威耶据各自独立用万有引力定律计算发现了“海王星”(第8个行星)。
2.1846年9月23日,德国的伽勒在勒维耶预言的位置发现这这颗行星,人们称其为---“”笔尖下发现的行星
3.1930年3月14日人们用同样的方法发现了— 冥王星
4.用类似的方法,人们又发现了太阳系及太阳系外的其他天体。1705年,英国天文学家哈雷根据万有引力定律计算了一颗著名彗星的轨道并正确预言了它的回归。这就是哈雷彗星。小结:基本思路2.将行星(或卫星)的运动看成
是匀速圆周运动.3.万有引力充当向心力 F引=F向.1. 在星体表面附近 F引=G重中心天体M转动天体m明确各个物理量天体半经R练习:1:利用下列哪组数据可以举算出地球的质量
( )
A:已知地球的半径r和地球表面的重力加速度g
B:已知卫星围绕地球运动的轨道半径r和周期T
C:已知卫星围绕地球运动的轨道半径r和周期T
D:已知卫星围绕地球运动的线速度V和周期TABCD2、月亮绕地球转动的周期为T、轨道半径为r,则由此可得地球质量的表达式为_________。(万有引力恒量为G)
3、如果某恒星有一颗卫星,此卫星沿非常靠近此恒星的表面做匀速圆周运动的周期为T,则可估算此恒星的平均密度为 。(万有引力恒量为G)太阳水星水星表面金星金星表面火星火星表面火星的卫星火星日出木星木星表面木星大气木卫1木卫4土星天王星海王星冥王星和卫星
◆ 那么太阳与地球之间的万有引力又是多大呢?已知:太阳的质量为M=2.0×1030kg,地球质量为m=6.0×1024kg,日地之间的距离为R=1.5×1011kmF=GMm/R23.5×1022N非常大,能够拉断直径为9000km的钢柱。=3.5×1022(N)而太阳对质量为50kg的人,引力很小,不到0.3N。
当然我们感受不到太阳的引力。=6.67×10-11×2.0×1030×6.0×1024/(1.5×1011)2 万有引力支配天体的运动 万有引力理论的成就万有引力提供天体圆运动的向心力万有引力定律对物理学、天文学的发展具有深远的影响;它把地面上物体运动的规律和天体运动的规律统一起来;对科学文化发展起到了积极的推动作用,解放了人们的思想,给人们探索自然的奥秘建立了极大信心,使人们有能力理解天地间的各种事物。时至今日,数千颗人造卫星正在按照万有引力定律为它们设定的轨道绕地球运转着。所以没有万有引力定律,就没有今天的天空漫步,当然也没有卫星通信时代了。以至于阿波罗8号从月球返航的途中,当地面控制中心问及“是谁在驾驶”的时候,指令长这样回答:“我想现在是牛顿在驾驶。”思考一:万有引力在天文学上有哪些方面的应用呢?“科学真是迷人”-测地球的质量问题一:如何测地球的质量? 天平能用吗?
问题一:如果要知道地球的质量,应该知道哪些条件?
当时已知:
地表重力加速度:g = 9.8m/s2
地球半径: R = 6400km
引力常量: G=6.67×10-11Nm2/kg2
一、“称量地球的质量”不考虑地球自转的影响所以说只要测出G就可以测出地球的质量。谁称出地球的质量?卡文迪许把数据代入具体算一下地球质量:地表重力加速度:g = 9.8m/s2
地球半径: R = 6400km
引力常量: G=6.67×10-11Nm2/kg2=6.0x1024kg思考:用同样的方法如何来测其它天体的质量呢?小结:求天体质量方法一:不考虑天体自转的影响:已知:三个量g、R、G三个量就可以求 一宇航员为了估测一星球的质量,他在该星球的表面做自由落体实验:让小球在离地面h高处自由下落,他测出经时间t小球落地,又已知该星球的半径为R,试估算该星球的质量。2hR2/Gt2练习一:思考二:如何才能知道太阳的质量呢?上面的方法可行吗?
能不能借用行星来称量呢?
请同学们看书后回答二、计算太阳的质量 我们可以测出太阳某行星的公转周期T、轨道半径r,能不能由此求出太阳的质量M?分析:
1.将行星的运动看成是匀速圆周运动.
2.万有引力充当向心力 F引=Fn.
只可求出中心天体的质量,
求不出环绕天体的质量。求天体质量方法二: 计算中心天体的质量情景: m(环绕天体)绕着M(中心天体)转,测出m运动周期T和离中心天体M的轨道半径r就可求出中心天体M: F引=Fn练习二:用上面方法如何求地球质量呢?已知 地球半径: R = 6400×103m
月亮周期: T = 27.3天≈2.36×106s
月亮轨道半径: r ≈ 60R,
求 地球的质量M? F引=Fn思考:如果不知道环绕天体的周期而是知道它的线速度或角速度,可以求中心天体质量吗?总结: 应用万有引力定律可以计算天体的质量:
(1)M=v2r/G.
(2)M=ω2r3/G.
(3)M=4π2r3/GT2.
(4) M=gR2/G.
ρ三、计算天体的密度 若环绕天体m接近中心天体M表面飞行则密度多少?r=R练习三;一艘宇宙飞船飞近一个不知名的行星,并进入靠近该行星表面的圆形轨道,宇航员进入预定的考察工作,宇航员能不能仅用一只表通过测定时间来测定该行星的密度?说明理由及推导过程四、发现未知天体背景:
1781年由英国物理学家威廉.赫歇尔发现了天王星,但人们观测到的天王星的运行轨迹与万有引力定律推测的结果有一些误差…… 天王星的运行轨道有些古怪 四、发现未知天体四、发现未知天体1:1845年英国人亚当斯和法国天文学家勒威耶据各自独立用万有引力定律计算发现了“海王星”(第8个行星)。
2.1846年9月23日,德国的伽勒在勒维耶预言的位置发现这这颗行星,人们称其为---“”笔尖下发现的行星
3.1930年3月14日人们用同样的方法发现了— 冥王星
4.用类似的方法,人们又发现了太阳系及太阳系外的其他天体。1705年,英国天文学家哈雷根据万有引力定律计算了一颗著名彗星的轨道并正确预言了它的回归。这就是哈雷彗星。小结:基本思路2.将行星(或卫星)的运动看成
是匀速圆周运动.3.万有引力充当向心力 F引=F向.1. 在星体表面附近 F引=G重中心天体M转动天体m明确各个物理量天体半经R练习:1:利用下列哪组数据可以举算出地球的质量
( )
A:已知地球的半径r和地球表面的重力加速度g
B:已知卫星围绕地球运动的轨道半径r和周期T
C:已知卫星围绕地球运动的轨道半径r和周期T
D:已知卫星围绕地球运动的线速度V和周期TABCD2、月亮绕地球转动的周期为T、轨道半径为r,则由此可得地球质量的表达式为_________。(万有引力恒量为G)
3、如果某恒星有一颗卫星,此卫星沿非常靠近此恒星的表面做匀速圆周运动的周期为T,则可估算此恒星的平均密度为 。(万有引力恒量为G)太阳水星水星表面金星金星表面火星火星表面火星的卫星火星日出木星木星表面木星大气木卫1木卫4土星天王星海王星冥王星和卫星
