29.3切线的性质和判定(1)课件(22张PPT)
文档属性
| 名称 | 29.3切线的性质和判定(1)课件(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-25 12:26:43 | ||
图片预览




文档简介
切线的性质
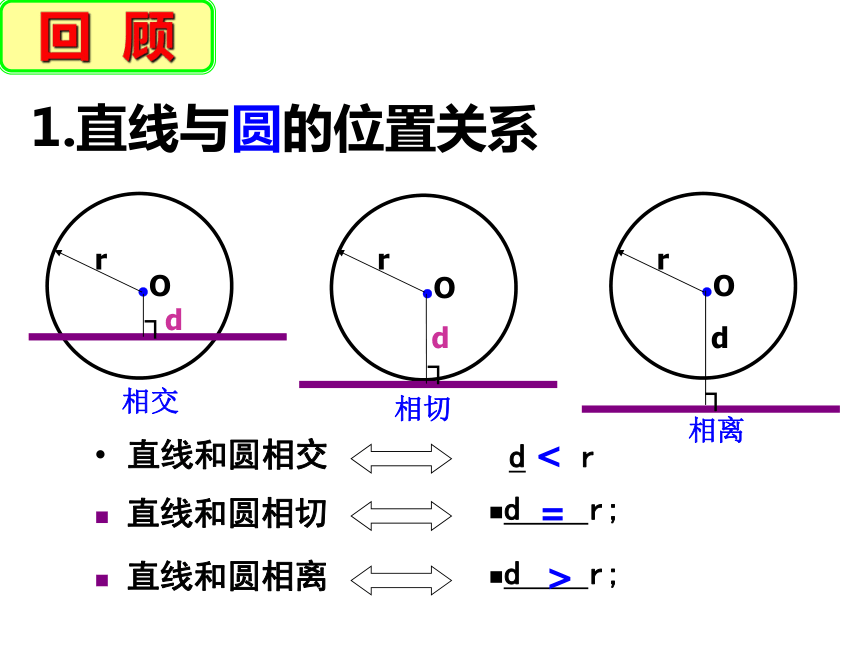
29.3与圆有关的位置关系
直线和圆相交
d r;
直线和圆相切
直线和圆相离
d r;
1.直线与圆的位置关系
d < r
=
>
回 顾
2.前面我们已学过的切线的性质有哪些?
答:
①、切线和圆有且只有一个公共点;
②、切线和圆心的距离等于半径。
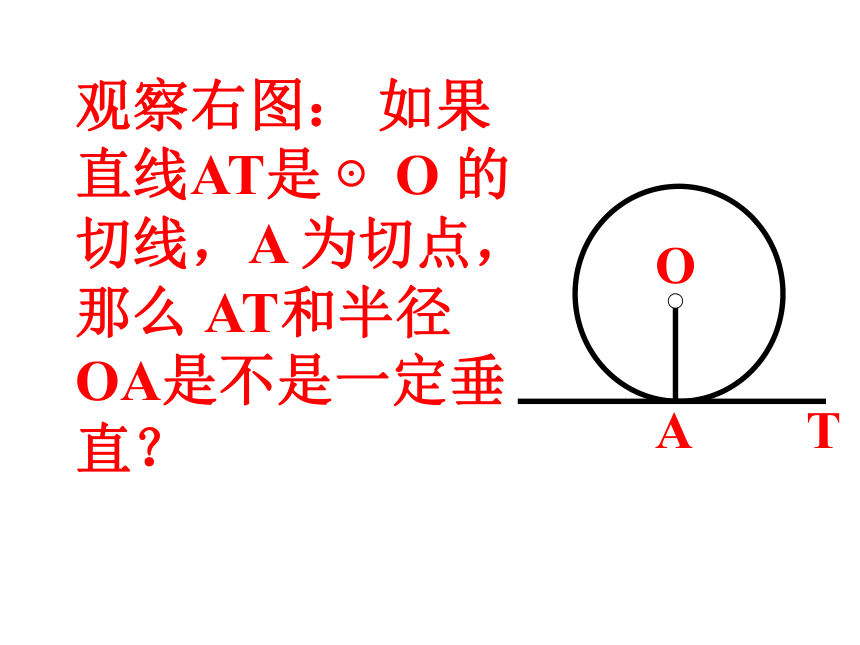
3.切线还有什么性质?
观察右图: 如果直线AT是 ⊙O 的切线,A 为切点,那么 AT和半径OA是不是一定垂直?
A
T
O
如果AT是 ⊙O 的切线,A 为切点,那么AT⊥OA.
你能说明理由吗?
O
M
反证法:假设AT与OA不垂直
则过点O作OM⊥AT,垂足为M
根据垂线段最短,得OM<OA
即圆心O到直线AT的距离d<R
∴直线AT 与⊙O 相交
这与已知“AT是 ⊙O 的切线”矛盾
∴假设不成立,即AT⊥OA
O
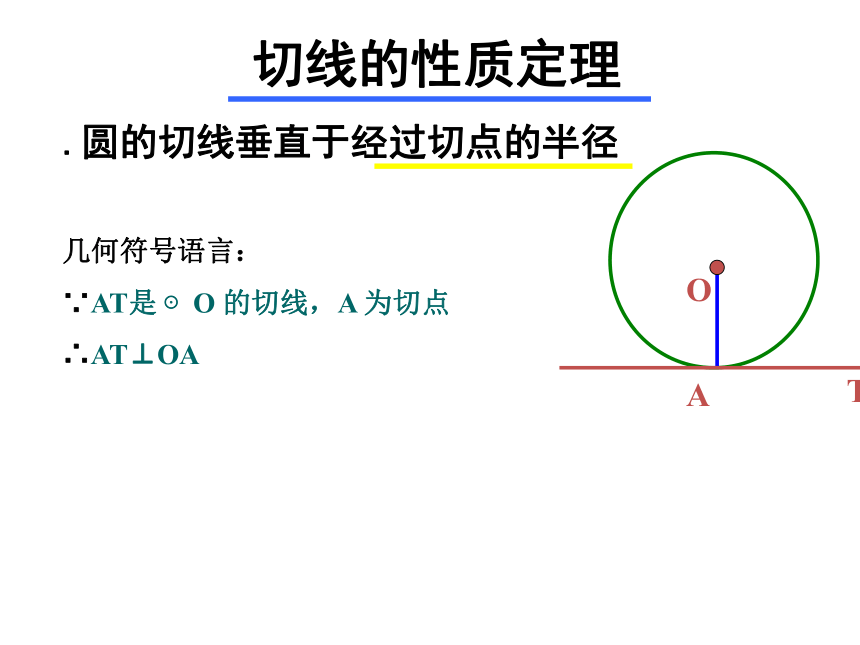
切线的性质定理
.圆的切线垂直于经过切点的半径
几何符号语言:
∵AT是 ⊙O 的切线,A 为切点
∴AT⊥OA
预备练习:
1、已知:如图:在△ABC中,AC与⊙O相切于点C,BC过圆心),∠BAC=63°,求∠ABC的度数。
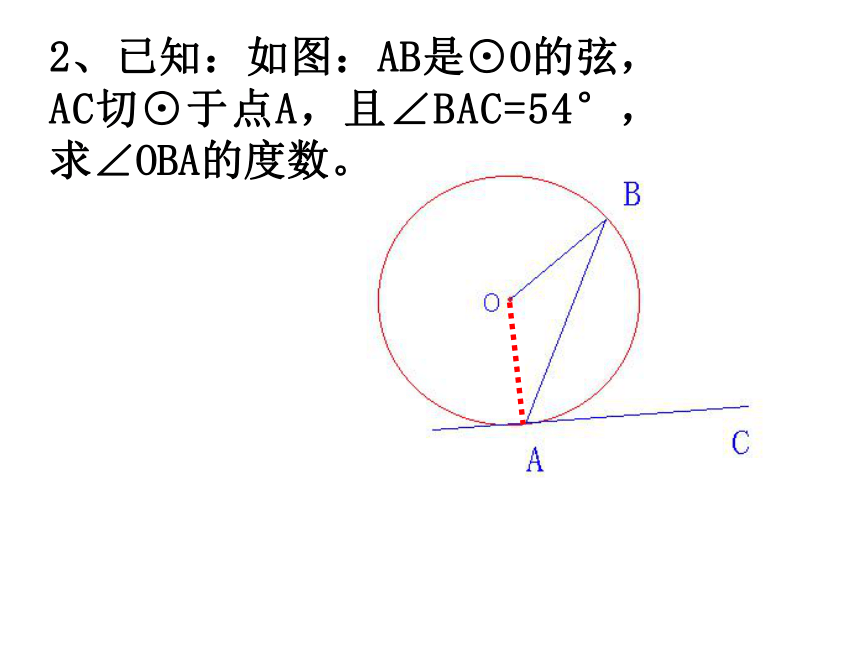
2、已知:如图:AB是⊙O的弦,AC切⊙于点A,且∠BAC=54°,求∠OBA的度数。
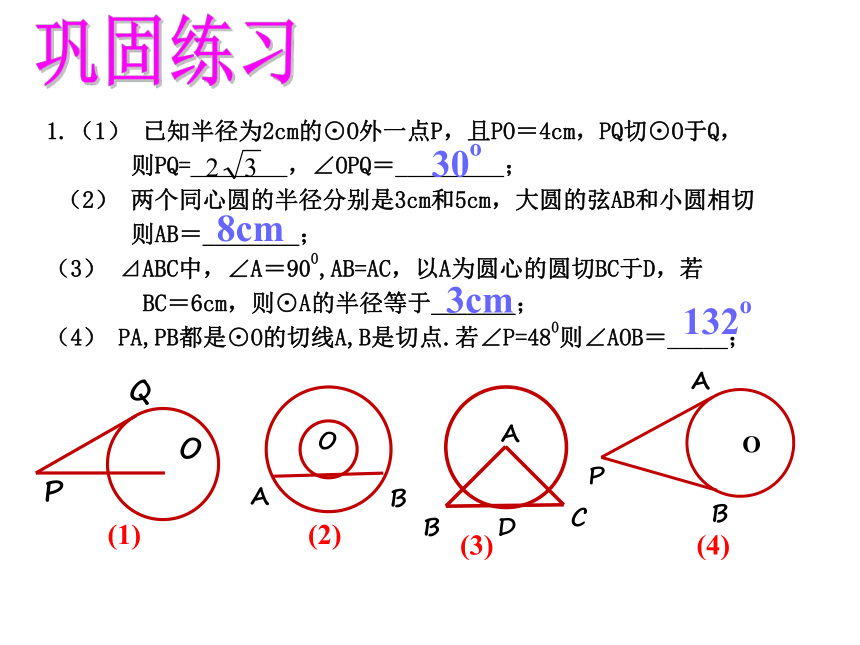
1.(1) 已知半径为2cm的⊙O外一点P,且PO=4cm,PQ切⊙O于Q,
则PQ=________,∠OPQ=_________;
?(2) 两个同心圆的半径分别是3cm和5cm,大圆的弦AB和小圆相切
则AB=________;
(3) ⊿ABC中,∠A=900,AB=AC,以A为圆心的圆切BC于D,若
BC=6cm,则⊙A的半径等于_______;
(4) PA,PB都是⊙O的切线A,B是切点.若∠P=480则∠AOB=_____;
30o
8cm
3cm
132o
2、求证:经过直径的两端点的圆的切线互相平行。
C
D
O
A
B
已知:如图,AB是圆O的直径,直线AC,BD分别是过点A,B的圆O的切线。
证明:如图,
AB 是⊙O的直径
∵AC、BD是⊙O的切线
∴AB⊥AC
AB⊥BD
∴AC∥BD
3
2
1
O
B
A
C
D
3.如图,AB为⊙O的直径, C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
4:如图, PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点(不与点A 、B 重合),若∠APB=40°,
求∠ACB的度数.
已知直线和圆相切时:常
连接切点与圆心。-----辅助线
若不给出图形,结果是否一样?
B
A
O
P
C
C
PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点(不与点A 、B 重合),若∠APB=40°,
求∠ACB的度数.
∠ACB=70°
,或 ∠ACB=110°
D
C
B
O
A
5 如图,在⊙O中,AB为直径, AD为弦, 过B点的切线与AD的延长线交于点C,且AD=DC
求∠ABD的度数.
解:∵ AB为直径
又∵BC为切线
∴∠ABC=90°
∵ △ABC为直角三角形
AD=DC
∴∠ADB=90°
∴AD=DB
∴△ABD为等腰直角三角形
∴∠ABD=45°
6:如图,在Rt△ABC中,∠C=90°,AE=4,AB=8,D是AB 上一点,以BD为直径的⊙O切AC于E,求AD的长.
7:如图,在平面直角坐标系中, 与Y轴相切于原点O,平行于X轴的直线交 于M、N两点,若点M的坐标是 ,则点N的坐标为________;
1、已知:AB是圆O的直径,C是AB延长线上的一点,CD切圆O于点D,DE⊥AB于点E。
求证: ∠CDB = ∠EDB
2、已知:AB是圆O的直径,AC 切圆O于点A,DE切圆O于点E,交AC于点D。求证:AD=CD
3:如果在地球赤道上空同样高度的位置上放置等距的三颗地球同步通信卫星,使卫星发射的信号刚好能够覆盖全部赤道,那么卫星高度应是多少?(地球半径R≈6370km)
分析:我们把赤道看成一个圆,同样高度且等距的三颗卫星的信号刚好覆盖全部赤道,等同于一个等边三角形的三边与赤道所在的圆都相切。
设三颗卫星分别位于点A,B,C处,这时,三个切点把圆三等分,每份圆弧为圆周的三分之一,易知:∠AOD=60°。
∵直线AB与圆相切于点D,
∴OD与直线AB垂直。
如右图:
设卫星高度为h,在Rt△AOD中,
cos60°=
即
解这个方程,得: H=R≈6370km。
因此,当三颗卫星的高度是6370km时,信号就能够覆盖全部赤道。
课堂小结
①切线和圆有且只有一个公共点
③圆的切线垂直于经过切点的半径
②切线和圆心的距离等于半径
切线性质
2.能运用切线性质定理进行计算与证明。
3.掌握常见的关于切线辅助线作法
29.3与圆有关的位置关系
直线和圆相交
d r;
直线和圆相切
直线和圆相离
d r;
1.直线与圆的位置关系
d < r
=
>
回 顾
2.前面我们已学过的切线的性质有哪些?
答:
①、切线和圆有且只有一个公共点;
②、切线和圆心的距离等于半径。
3.切线还有什么性质?
观察右图: 如果直线AT是 ⊙O 的切线,A 为切点,那么 AT和半径OA是不是一定垂直?
A
T
O
如果AT是 ⊙O 的切线,A 为切点,那么AT⊥OA.
你能说明理由吗?
O
M
反证法:假设AT与OA不垂直
则过点O作OM⊥AT,垂足为M
根据垂线段最短,得OM<OA
即圆心O到直线AT的距离d<R
∴直线AT 与⊙O 相交
这与已知“AT是 ⊙O 的切线”矛盾
∴假设不成立,即AT⊥OA
O
切线的性质定理
.圆的切线垂直于经过切点的半径
几何符号语言:
∵AT是 ⊙O 的切线,A 为切点
∴AT⊥OA
预备练习:
1、已知:如图:在△ABC中,AC与⊙O相切于点C,BC过圆心),∠BAC=63°,求∠ABC的度数。
2、已知:如图:AB是⊙O的弦,AC切⊙于点A,且∠BAC=54°,求∠OBA的度数。
1.(1) 已知半径为2cm的⊙O外一点P,且PO=4cm,PQ切⊙O于Q,
则PQ=________,∠OPQ=_________;
?(2) 两个同心圆的半径分别是3cm和5cm,大圆的弦AB和小圆相切
则AB=________;
(3) ⊿ABC中,∠A=900,AB=AC,以A为圆心的圆切BC于D,若
BC=6cm,则⊙A的半径等于_______;
(4) PA,PB都是⊙O的切线A,B是切点.若∠P=480则∠AOB=_____;
30o
8cm
3cm
132o
2、求证:经过直径的两端点的圆的切线互相平行。
C
D
O
A
B
已知:如图,AB是圆O的直径,直线AC,BD分别是过点A,B的圆O的切线。
证明:如图,
AB 是⊙O的直径
∵AC、BD是⊙O的切线
∴AB⊥AC
AB⊥BD
∴AC∥BD
3
2
1
O
B
A
C
D
3.如图,AB为⊙O的直径, C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
4:如图, PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点(不与点A 、B 重合),若∠APB=40°,
求∠ACB的度数.
已知直线和圆相切时:常
连接切点与圆心。-----辅助线
若不给出图形,结果是否一样?
B
A
O
P
C
C
PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点(不与点A 、B 重合),若∠APB=40°,
求∠ACB的度数.
∠ACB=70°
,或 ∠ACB=110°
D
C
B
O
A
5 如图,在⊙O中,AB为直径, AD为弦, 过B点的切线与AD的延长线交于点C,且AD=DC
求∠ABD的度数.
解:∵ AB为直径
又∵BC为切线
∴∠ABC=90°
∵ △ABC为直角三角形
AD=DC
∴∠ADB=90°
∴AD=DB
∴△ABD为等腰直角三角形
∴∠ABD=45°
6:如图,在Rt△ABC中,∠C=90°,AE=4,AB=8,D是AB 上一点,以BD为直径的⊙O切AC于E,求AD的长.
7:如图,在平面直角坐标系中, 与Y轴相切于原点O,平行于X轴的直线交 于M、N两点,若点M的坐标是 ,则点N的坐标为________;
1、已知:AB是圆O的直径,C是AB延长线上的一点,CD切圆O于点D,DE⊥AB于点E。
求证: ∠CDB = ∠EDB
2、已知:AB是圆O的直径,AC 切圆O于点A,DE切圆O于点E,交AC于点D。求证:AD=CD
3:如果在地球赤道上空同样高度的位置上放置等距的三颗地球同步通信卫星,使卫星发射的信号刚好能够覆盖全部赤道,那么卫星高度应是多少?(地球半径R≈6370km)
分析:我们把赤道看成一个圆,同样高度且等距的三颗卫星的信号刚好覆盖全部赤道,等同于一个等边三角形的三边与赤道所在的圆都相切。
设三颗卫星分别位于点A,B,C处,这时,三个切点把圆三等分,每份圆弧为圆周的三分之一,易知:∠AOD=60°。
∵直线AB与圆相切于点D,
∴OD与直线AB垂直。
如右图:
设卫星高度为h,在Rt△AOD中,
cos60°=
即
解这个方程,得: H=R≈6370km。
因此,当三颗卫星的高度是6370km时,信号就能够覆盖全部赤道。
课堂小结
①切线和圆有且只有一个公共点
③圆的切线垂直于经过切点的半径
②切线和圆心的距离等于半径
切线性质
2.能运用切线性质定理进行计算与证明。
3.掌握常见的关于切线辅助线作法
