专题07+逆向思维法-高中物理八大解题方法+Word版含解析
文档属性
| 名称 | 专题07+逆向思维法-高中物理八大解题方法+Word版含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 26.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-09-25 12:11:19 | ||
图片预览

文档简介
高中物理解题方法之逆向思维法
内容提要:本文通过几道物理题的解法分析,阐述逆向思维解题方法的几种应用:一、在解题程序上逆向思维;二、在因果关系上逆向思维;三、在迁移规律上逆向思维。
所谓“逆向思维”,简单说来就是“倒过来想一想”。这种方法用于解物理题,特别是某些难题,很有好处。下面通过高考物理试卷中的几道题的解法分析,谈谈逆向思维解题法的应用的几种情况。
在解题程序上逆向思维
解题程序,一般是从已知到未知,一步步求解,通常称为正向思维。但有些题目反过来思考,从未知到已知逐步推理,反而方便些。
例1.如图1所示,
图1
一理想变压器的原副线圈分别由双线圈ab和cd(匝数都为n1)、ef和gh(匝数都为n2)组成。用I1和U1表示输入电流和电压,用I2和U2表示输出电流和电压。在下列四种接法中,符合关系的有:
b与c相连,以a、d为输入端;f与g相连,以e、h为输入端。
b与c相连,以a、d为输入端;e与g相连、f与h相连作为输入端。
a与c相连,b与d相连作为输入端;f与g相连,以e、h为输出端。
a与c相连,b与d相连作为输入端;e与g相连、f与h相连作为输出端。
析与解:一般的选择题,是从题干所给的已知条件去求解,解出结果与选项比较,哪个正确选哪个。但本题我们不能根据两个公式去求解法,而只能逐一选项讨论哪种解法能得出题干给出的公式。
对(A),初级ab和cd两线圈串联,总匝数为2 n1,次级ef和gh两线圈亦串联,总匝数为2 n2,据变压器变压比公式及变流比公式有。
对(B),初级总匝数为2 n1,次级总匝数为n2(ef与gh并联),不符合题给两公式。
对(C),初级总匝数为n1,次级总匝数为2n2,亦不符合题给两公式。
对(D),初级总匝数为 n1,次级总匝数为n2 , 符合题给两公式。
故本题选(A、D)。
这种在解题程序上的逆向思维法,较多用于选择题和证明题,因为此类题给出了要求的结果,便于逆推。
二、在因果关系上逆向思维
物理过程有一定的因果关系,通常从原因出发推导结果,称为正向思维。但有时反过来,从结果倒推原因,可称为逆向思维。
例2.某人透过焦距为10厘米,直径为4.0厘米的薄凸透镜观看方格纸,每个方格的边长均为0.30厘米。他使透镜的主轴与方格垂直,透镜与纸面相距10厘米,眼睛位于透镜主轴上离透镜5.0厘米处。问他至多能看到同一行上几个完整的方格?
析与解:眼睛看到方格,应是方格纸反射的自然光经透镜折射后射到人的眼中,我们根据光路的可逆性,把眼睛看作光源,求此光源发出的光经透镜折射(会聚)后能照到方格纸上多大的范围?
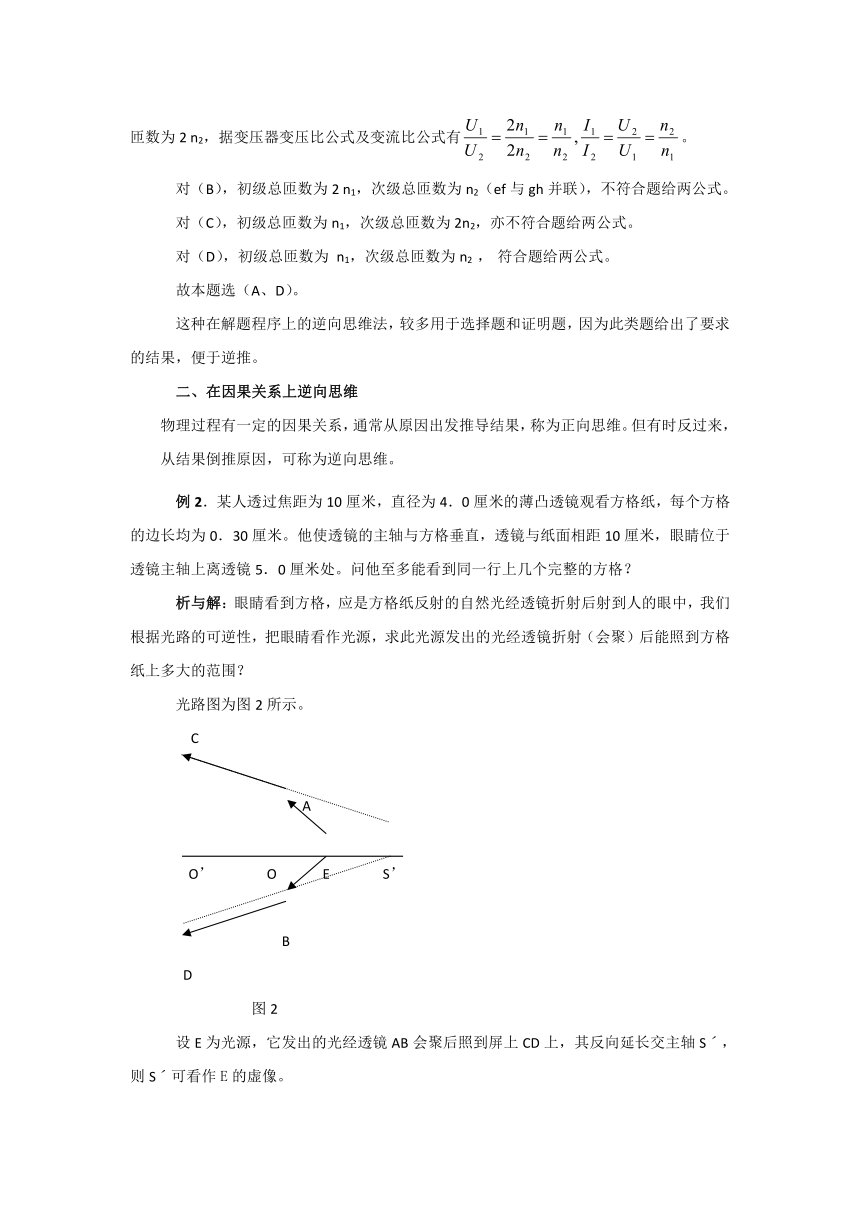
光路图为图2所示。
C
A
O’ O E S’
B
D
图2
设E为光源,它发出的光经透镜AB会聚后照到屏上CD上,其反向延长交主轴Sˊ,则Sˊ可看作E的虚像。
据透镜成像公式得像距v为:厘米。
由图2,相似三角形SˊA B与SˊC D中,,
C D=2A B=2(厘米)。
C D中包含的方格数至多为(个)其中a为每个方格的边长。
有同学问:把物体放在焦点处不是不能成像吗?笔者一提示:用逆向思维法。同学恍然大悟。可见对物理知识,切忌死记硬背现成的结论。
此类逆推法也应用不少。例如在碰撞中,已知物体碰撞后的速度求碰撞前的速度,在电磁感应中,已知感生电流的方向求导体如何运动等等。
三、在迁移规律上逆向思维
在见到一个新题后,有时会联想到以前解过的题目或已有的物理知识、物理情境,把“陈题”的思维方法应用到“新题”上,称为“迁移”。但有时“新题”与“陈题”的关系是互逆关系,即在新题中为已知的,在陈题中为所求,在新题中为所求的,在陈题中为已知。这就要求用逆向思维去迁移。
例3.有一准确的杆秤。今只给你一把有刻度的直尺,要求用它测出这杆秤的秤砣的质量。试导出表示秤砣质量的公式,并说明所需测量的量。
这是一道考查考生独立思维能力的题,已知条件甚少,许多同学无从下手。
看到此题后,首先应该联想到课本上制作杆秤的小实验(见《物理》课本上册P36—37),小实验是给出秤秤和已知质量的秤砣,用实验法找出秤杆上各个刻度的位置,其中首先找出零刻度的位置。本题逆其向而行之,已知秤杆上的刻度,求秤砣的质量。这里,秤杆上的各刻度是已知量,是隐含的已知量。
解:秤的结构如图3所示。
图3
秤钩B到提钮的距离为d,零刻度(即定盘星)A到提钮的距离为0,满刻度D到提钮的距离为,秤杆和秤钩所受的重力为P,秤水平时,P对提钮的力臂为d0,设秤砣的质量为m,秤的最大称量为M。
当空称平衡时,有 mg0=Pd0 ①
当满称量平衡时有 Mgd=Pd0+mg ②
解①、② 式得: ③
或 ④
本题的答案是③式,从秤杆上读出最大称量M,用直尺测出d和从A到D的距离(),代入③式即可求得m。
小实验的答案是④式,即已知秤砣的质量m和d,用试验法找出()的位置D。从③式与④式的比较中可看出,二者是互逆的过程。
四、在命题方法上逆向思维
逆向思维就是在题目中已知原因判结果与已知结果判原因之间的变换。逆向思维的应用很广泛,如动力学,已知物体运动特点或运动图像,受力应有何特点?电磁感应现象,如图4,一通电直导线附近放置一导线框,导线框与直导线在一个平面内,什么情况下可以使导线框中产生顺时针的感应电流?振动及波动现象,若两相干波源振动相反,则加强和减弱的条件如何?电学,根据电路特点判断电流的情况等等。
?
例4.如图5,若x轴表示时间,y轴表示位置,则该图象反映了某质点做匀速直线运动时,位置与时间的关系.若令x轴和y轴分别表示其他的物理量,则该图象又可以反映在某种情况下,相应的物理量之间的关系。下列说法中正确的是( )
A.若x轴表示时间,y轴表示动能,则该图象可以反映某物体受恒定合外力作用做直线运动过程中,物体动能与时间的关系
B.若x轴表示频率,y轴表示动能,则该图象可以反映光电效应中,光电子最大初动能与入射光频率之间的关系
C.若x轴表示时间,y轴表示动量,则该图象可以反映某物体在沿运动方向的恒定合外力作用下,物体动量与时间的关系
D.若x轴表示时间,y轴表示感应电动势,则该图象可以反映静置于磁场中的某闭合回路,当磁感应强度随时间均匀增大时,闭合回路的感应电动势与时间的关系
【答案】C
点评:本题考查动能定理、爱因斯坦光电效应方程、动量定理、法拉第电磁感应定律中的物理图像。根据物理规律画图象学生平时训练很多,可以说熟练掌握,而此题通过图象分析物理规律。这类新题与已有习题思维过程反向,考查学生对物理规律的形成过程是否掌握,更好的锻炼学生的逆向思维能力,符合新课改精神注重过程与方法的要求。
把好的题加以变形或推广,换一个面貌出现,这是常用的命题方法,叫命题转换。逆向思维法是探求转换命题的解法的途径。
内容提要:本文通过几道物理题的解法分析,阐述逆向思维解题方法的几种应用:一、在解题程序上逆向思维;二、在因果关系上逆向思维;三、在迁移规律上逆向思维。
所谓“逆向思维”,简单说来就是“倒过来想一想”。这种方法用于解物理题,特别是某些难题,很有好处。下面通过高考物理试卷中的几道题的解法分析,谈谈逆向思维解题法的应用的几种情况。
在解题程序上逆向思维
解题程序,一般是从已知到未知,一步步求解,通常称为正向思维。但有些题目反过来思考,从未知到已知逐步推理,反而方便些。
例1.如图1所示,
图1
一理想变压器的原副线圈分别由双线圈ab和cd(匝数都为n1)、ef和gh(匝数都为n2)组成。用I1和U1表示输入电流和电压,用I2和U2表示输出电流和电压。在下列四种接法中,符合关系的有:
b与c相连,以a、d为输入端;f与g相连,以e、h为输入端。
b与c相连,以a、d为输入端;e与g相连、f与h相连作为输入端。
a与c相连,b与d相连作为输入端;f与g相连,以e、h为输出端。
a与c相连,b与d相连作为输入端;e与g相连、f与h相连作为输出端。
析与解:一般的选择题,是从题干所给的已知条件去求解,解出结果与选项比较,哪个正确选哪个。但本题我们不能根据两个公式去求解法,而只能逐一选项讨论哪种解法能得出题干给出的公式。
对(A),初级ab和cd两线圈串联,总匝数为2 n1,次级ef和gh两线圈亦串联,总匝数为2 n2,据变压器变压比公式及变流比公式有。
对(B),初级总匝数为2 n1,次级总匝数为n2(ef与gh并联),不符合题给两公式。
对(C),初级总匝数为n1,次级总匝数为2n2,亦不符合题给两公式。
对(D),初级总匝数为 n1,次级总匝数为n2 , 符合题给两公式。
故本题选(A、D)。
这种在解题程序上的逆向思维法,较多用于选择题和证明题,因为此类题给出了要求的结果,便于逆推。
二、在因果关系上逆向思维
物理过程有一定的因果关系,通常从原因出发推导结果,称为正向思维。但有时反过来,从结果倒推原因,可称为逆向思维。
例2.某人透过焦距为10厘米,直径为4.0厘米的薄凸透镜观看方格纸,每个方格的边长均为0.30厘米。他使透镜的主轴与方格垂直,透镜与纸面相距10厘米,眼睛位于透镜主轴上离透镜5.0厘米处。问他至多能看到同一行上几个完整的方格?
析与解:眼睛看到方格,应是方格纸反射的自然光经透镜折射后射到人的眼中,我们根据光路的可逆性,把眼睛看作光源,求此光源发出的光经透镜折射(会聚)后能照到方格纸上多大的范围?
光路图为图2所示。
C
A
O’ O E S’
B
D
图2
设E为光源,它发出的光经透镜AB会聚后照到屏上CD上,其反向延长交主轴Sˊ,则Sˊ可看作E的虚像。
据透镜成像公式得像距v为:厘米。
由图2,相似三角形SˊA B与SˊC D中,,
C D=2A B=2(厘米)。
C D中包含的方格数至多为(个)其中a为每个方格的边长。
有同学问:把物体放在焦点处不是不能成像吗?笔者一提示:用逆向思维法。同学恍然大悟。可见对物理知识,切忌死记硬背现成的结论。
此类逆推法也应用不少。例如在碰撞中,已知物体碰撞后的速度求碰撞前的速度,在电磁感应中,已知感生电流的方向求导体如何运动等等。
三、在迁移规律上逆向思维
在见到一个新题后,有时会联想到以前解过的题目或已有的物理知识、物理情境,把“陈题”的思维方法应用到“新题”上,称为“迁移”。但有时“新题”与“陈题”的关系是互逆关系,即在新题中为已知的,在陈题中为所求,在新题中为所求的,在陈题中为已知。这就要求用逆向思维去迁移。
例3.有一准确的杆秤。今只给你一把有刻度的直尺,要求用它测出这杆秤的秤砣的质量。试导出表示秤砣质量的公式,并说明所需测量的量。
这是一道考查考生独立思维能力的题,已知条件甚少,许多同学无从下手。
看到此题后,首先应该联想到课本上制作杆秤的小实验(见《物理》课本上册P36—37),小实验是给出秤秤和已知质量的秤砣,用实验法找出秤杆上各个刻度的位置,其中首先找出零刻度的位置。本题逆其向而行之,已知秤杆上的刻度,求秤砣的质量。这里,秤杆上的各刻度是已知量,是隐含的已知量。
解:秤的结构如图3所示。
图3
秤钩B到提钮的距离为d,零刻度(即定盘星)A到提钮的距离为0,满刻度D到提钮的距离为,秤杆和秤钩所受的重力为P,秤水平时,P对提钮的力臂为d0,设秤砣的质量为m,秤的最大称量为M。
当空称平衡时,有 mg0=Pd0 ①
当满称量平衡时有 Mgd=Pd0+mg ②
解①、② 式得: ③
或 ④
本题的答案是③式,从秤杆上读出最大称量M,用直尺测出d和从A到D的距离(),代入③式即可求得m。
小实验的答案是④式,即已知秤砣的质量m和d,用试验法找出()的位置D。从③式与④式的比较中可看出,二者是互逆的过程。
四、在命题方法上逆向思维
逆向思维就是在题目中已知原因判结果与已知结果判原因之间的变换。逆向思维的应用很广泛,如动力学,已知物体运动特点或运动图像,受力应有何特点?电磁感应现象,如图4,一通电直导线附近放置一导线框,导线框与直导线在一个平面内,什么情况下可以使导线框中产生顺时针的感应电流?振动及波动现象,若两相干波源振动相反,则加强和减弱的条件如何?电学,根据电路特点判断电流的情况等等。
?
例4.如图5,若x轴表示时间,y轴表示位置,则该图象反映了某质点做匀速直线运动时,位置与时间的关系.若令x轴和y轴分别表示其他的物理量,则该图象又可以反映在某种情况下,相应的物理量之间的关系。下列说法中正确的是( )
A.若x轴表示时间,y轴表示动能,则该图象可以反映某物体受恒定合外力作用做直线运动过程中,物体动能与时间的关系
B.若x轴表示频率,y轴表示动能,则该图象可以反映光电效应中,光电子最大初动能与入射光频率之间的关系
C.若x轴表示时间,y轴表示动量,则该图象可以反映某物体在沿运动方向的恒定合外力作用下,物体动量与时间的关系
D.若x轴表示时间,y轴表示感应电动势,则该图象可以反映静置于磁场中的某闭合回路,当磁感应强度随时间均匀增大时,闭合回路的感应电动势与时间的关系
【答案】C
点评:本题考查动能定理、爱因斯坦光电效应方程、动量定理、法拉第电磁感应定律中的物理图像。根据物理规律画图象学生平时训练很多,可以说熟练掌握,而此题通过图象分析物理规律。这类新题与已有习题思维过程反向,考查学生对物理规律的形成过程是否掌握,更好的锻炼学生的逆向思维能力,符合新课改精神注重过程与方法的要求。
把好的题加以变形或推广,换一个面貌出现,这是常用的命题方法,叫命题转换。逆向思维法是探求转换命题的解法的途径。
同课章节目录
