动量和能量综合训练
图片预览



文档简介
动量和能量综合训练
1、如图1所示,在光滑的水平面上,静放着一个质量为M=980g的长方形匀质木块,现有一颗质量为m=20g的子弹以300m/s的水平速度沿木块的轴线射向木块,结果子弹留在木块中没有射出,和木块一起以共同共速度运动。已知木块沿子弹运动方向的厚度为L=10cm,子弹射入的深度为d=6cm。设木块对子弹的阻力保持不变。
(1)求子弹和木块的共同速度以及它们在此过程中所增加的内能;
(2)若子弹以400m/s的水平速度从同一方向水平射向该木块时,则它能否穿透该木块?
2、一个人站在静止于光滑平直轨道的平板车上,人和车的总质量为M=80kg,现在让此人双手各握一个质量均为m=10kg的铅球,以两种方式顺首轨道方向水平投出铅球:第一次是一个一个地投;第二次是两个一起投。设每次投掷时铅球相对车的速度相同,求前后两次投掷铅球后小车获得的速度之比。
3、如图2所示,两木块A、B由轻弹簧连接,起初静止于光滑水平面上。某时刻一粒子弹以水平速度v0射入木块A并留在其中,子弹打入木块的过程持续时间极短,可不考虑此过程中木块A的位移。已知木块A的质量为(M—m),木块B的质量为M,子弹的质量为m,弹簧原长为L0,劲度系数为k,弹簧的弹性势能与形变量的对应关系为。如果此后运动过程中弹簧始终处于弹性限度内,且木块A、B不会发生直接碰撞。试求:
(1)当弹簧压缩到最短时,木块B的速度大小;
(2)运动中弹簧出的最大长度。
4、质量为M的小车静止在光滑的水平布。小车上表面是一个光滑的曲面,末端上水平的,如图所示,小车被挡板P挡住,质量为m的物体从距地面高度为H处自由落下,然后沿光滑曲面继续下滑,物体的落地点与小车右端距离为S0,若撤去挡板P,物体仍从原处自由落下,求物体落地点与小车右端的距离是多少?
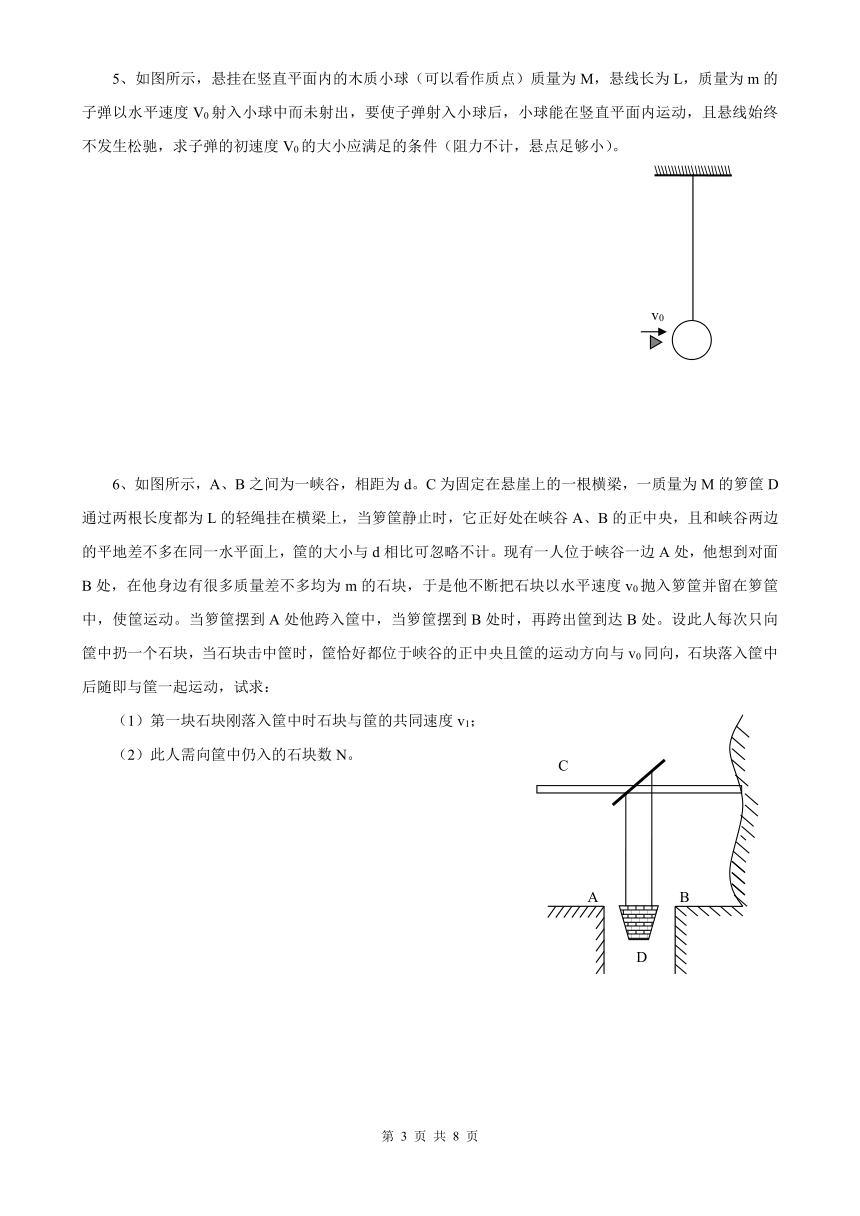
5、如图所示,悬挂在竖直平面内的木质小球(可以看作质点)质量为M,悬线长为L,质量为m的子弹以水平速度V0射入小球中而未射出,要使子弹射入小球后,小球能在竖直平面内运动,且悬线始终不发生松驰,求子弹的初速度V0的大小应满足的条件(阻力不计,悬点足够小)。
6、如图所示,A、B之间为一峡谷,相距为d。C为固定在悬崖上的一根横梁,一质量为M的箩筐D通过两根长度都为L的轻绳挂在横梁上,当箩筐静止时,它正好处在峡谷A、B的正中央,且和峡谷两边的平地差不多在同一水平面上,筐的大小与d相比可忽略不计。现有一人位于峡谷一边A处,他想到对面B处,在他身边有很多质量差不多均为m的石块,于是他不断把石块以水平速度v0抛入箩筐并留在箩筐中,使筐运动。当箩筐摆到A处他跨入筐中,当箩筐摆到B处时,再跨出筐到达B处。设此人每次只向筐中扔一个石块,当石块击中筐时,筐恰好都位于峡谷的正中央且筐的运动方向与v0同向,石块落入筐中后随即与筐一起运动,试求:
(1)第一块石块刚落入筐中时石块与筐的共同速度v1;
(2)此人需向筐中仍入的石块数N。
7、有一内表面光滑的金属盒,底面长L=1.2m,质量为m1=0.5kg,放在水平面上,与水平面间的动摩擦因数μ=1/8,在盒内最右端放一个半径为r=0.1m的光滑金属球,质量为m2=0.5kg。现在盒最左端给盒施加一个水平冲量I =1.5N·s,如图所示(盒壁厚度,球与盒发生碰撞的时间和能量损失不计)。g=10m/s2,求:
(1)金属盒能在地面上运动多远?
(2)金属盒从开始运动到最后静止所经历的时间多长?
8、n个相同的木块,每块的质量都是m,放置在倾角为θ的斜面上,相邻两木块间的距离为L,最下端的木块距斜面底端也是L,木块与斜面间的动摩擦因数为μ,如图所示。在开始时刻,第一块木块以初速度v0沿斜面下滑,其余所有的木块都静止。由于第一个木块的下滑将依次引起一系列的碰撞,在每次发生碰撞后,发生碰撞的木块都粘在一起运动,直到最后第n个木块到达斜面底端时,刚好停在底端。求:
(1)第一次碰撞前第一个木块的动能Ek1;
(2)第一次碰撞时系统损失的机械能△E1与Ek1的比值;
(3)在整个过程中由于碰撞而损失的总机械能△E。
答案
1、(1)设子弹的初速度为v0,射入木块后两者的共同速度为v,以子弹和木块为系统,由动量守恒定律,有: v=
此过程系统所增加的内能为:
(2)设子弹以的速度刚好能够射穿材料相同、厚度为的另一木块。则对子弹和木块组成的系统,由动量守恒定律有:
此过程系统所损耗的机械能为:
由功能关系有:
故: 于是: 所以能射穿此木块。
2、设每次投掷时铅球相对车的速度为u,前一种方式投出一个球后,车速为,由动量守恒定律得:
投出第二个球后,车速为,由动量守恒定律得:
后一种方式投出球后,车速为,由动量守恒定律得:
故前后两次投掷铅球后小车获得的速度之比为:
3、(1)子弹打入木块以及木块运动的整个过程中,子弹和两木块组成的系统动量守恒,当弹簧压缩到最短时,A、B的速度相等,设为,则:
(2)子弹打入木块A的过程中,子弹和木块组成的系统动量守恒,设二者的共同速度为,则:
,
当弹簧达到最大长度时两木块速度相等,由动量守恒定律得:
从子弹射入木块A到两者具有共同速度以后的运动过程中,系统机械能守恒,故:
弹簧的最大长度为:
4、设小车被挡板挡住时,物体离开小车的水平速度为,从抛出点到落地点时间为,抛出点到落地点的高度为,则机械能守恒有: (1)
由平抛运动规律有: (2)
撤去挡板后,物体离开小车时车速大小为,物体速为,则由机械能守恒有:
(3)
由动量守恒有: (4)
由平抛运动规律有: (h不变,t不变) (5)
由(1)(3)(4)得:
由(2)式有,将、、代入(5)式得:
5、子弹射入小球前后,由动量守恒定律得: (1)
子弹射入小球后,小球上摆的高时小球的运动符合题意,设小球上摆的高度正好为,由机械能守恒得: (2)
由(1)(2)式得:
故,当时,小球在竖直平面内运动,绳不会松驰。
子弹射入小球后,若小球恰好能摆到2L的高度,则小球在竖直平面内做圆运动。设小球到达畅通高点时的速度为,则有: (3)
由机械能守恒得: (4)
由(1)(3)(4)得:
故当时,小球在竖直平面内做圆周运动,绳也不会松驰。
6、(1)设第一块石块扔入箩筐后,筐开始运动的速度为,由动量守恒定律有:
① ②
(2)第二块石块扔入箩筐时,由动量守恒定律有:
③ 由②③式得: ④
当第n个石块扔入筐时,筐的速度为: ⑤
若箩筐具有速度后恰能摆到A处,此时筐上升的高度为,由机械能守恒定律得:
⑥ ⑦
解⑤⑥⑦式得:
7、(1)由冲量的作用,,金属盒所受的摩擦力为:
,设它能在地面上滑行S(m),则由动能定理得:
解得:
(2)当盒前进时与球发生碰撞,设碰前盒的速度为,碰后的速度为,球碰后的速度为,则对盒用动能定理得: 解得:
由碰撞过程动量守恒和能量守恒有:
联立以上三式得:。同时,当球与盒再次碰撞时,球静止,盒以的速度前进,,所以不会再与球碰撞,则盒运动的时间可由动量定理求得:
解得:
在盒与球两次碰撞之间还有一段时间为小球在运动,
则金属盒从开始运动到最后静止所经历的时间为:
8、(1)依题意,最后一个木块停在斜面底端,表明木块除碰撞以外其它时间内所受合外力与运动方向相反,木块沿斜面做匀减速运动,设其加速度大小为,方向沿斜面向上,则:
①
第一次碰撞前第一个木块的动能为: ②
①式代入②式得: ③
(2)1、2两木块碰撞过程中动量守恒,有: ④ ⑤
上述过程中损失的机械能为: ⑥
解得: ⑦
由①式可知木块下滑的加速度与木块质量无关,从第1个木块开始下滑的整个过程中,除每一次碰撞的瞬间外,下滑加速度均为,方向沿斜面向上;在整个过程中,第n个木块运动距离为L,第n-1个木块运动的距离为2L,……第1个木块运动距离为nL,除碰撞瞬间外各木块克服合外力做功为:
⑧
整个过程中,各次碰撞损失的总机械能为: ⑨
由①⑧⑨式得:
1、如图1所示,在光滑的水平面上,静放着一个质量为M=980g的长方形匀质木块,现有一颗质量为m=20g的子弹以300m/s的水平速度沿木块的轴线射向木块,结果子弹留在木块中没有射出,和木块一起以共同共速度运动。已知木块沿子弹运动方向的厚度为L=10cm,子弹射入的深度为d=6cm。设木块对子弹的阻力保持不变。
(1)求子弹和木块的共同速度以及它们在此过程中所增加的内能;
(2)若子弹以400m/s的水平速度从同一方向水平射向该木块时,则它能否穿透该木块?
2、一个人站在静止于光滑平直轨道的平板车上,人和车的总质量为M=80kg,现在让此人双手各握一个质量均为m=10kg的铅球,以两种方式顺首轨道方向水平投出铅球:第一次是一个一个地投;第二次是两个一起投。设每次投掷时铅球相对车的速度相同,求前后两次投掷铅球后小车获得的速度之比。
3、如图2所示,两木块A、B由轻弹簧连接,起初静止于光滑水平面上。某时刻一粒子弹以水平速度v0射入木块A并留在其中,子弹打入木块的过程持续时间极短,可不考虑此过程中木块A的位移。已知木块A的质量为(M—m),木块B的质量为M,子弹的质量为m,弹簧原长为L0,劲度系数为k,弹簧的弹性势能与形变量的对应关系为。如果此后运动过程中弹簧始终处于弹性限度内,且木块A、B不会发生直接碰撞。试求:
(1)当弹簧压缩到最短时,木块B的速度大小;
(2)运动中弹簧出的最大长度。
4、质量为M的小车静止在光滑的水平布。小车上表面是一个光滑的曲面,末端上水平的,如图所示,小车被挡板P挡住,质量为m的物体从距地面高度为H处自由落下,然后沿光滑曲面继续下滑,物体的落地点与小车右端距离为S0,若撤去挡板P,物体仍从原处自由落下,求物体落地点与小车右端的距离是多少?
5、如图所示,悬挂在竖直平面内的木质小球(可以看作质点)质量为M,悬线长为L,质量为m的子弹以水平速度V0射入小球中而未射出,要使子弹射入小球后,小球能在竖直平面内运动,且悬线始终不发生松驰,求子弹的初速度V0的大小应满足的条件(阻力不计,悬点足够小)。
6、如图所示,A、B之间为一峡谷,相距为d。C为固定在悬崖上的一根横梁,一质量为M的箩筐D通过两根长度都为L的轻绳挂在横梁上,当箩筐静止时,它正好处在峡谷A、B的正中央,且和峡谷两边的平地差不多在同一水平面上,筐的大小与d相比可忽略不计。现有一人位于峡谷一边A处,他想到对面B处,在他身边有很多质量差不多均为m的石块,于是他不断把石块以水平速度v0抛入箩筐并留在箩筐中,使筐运动。当箩筐摆到A处他跨入筐中,当箩筐摆到B处时,再跨出筐到达B处。设此人每次只向筐中扔一个石块,当石块击中筐时,筐恰好都位于峡谷的正中央且筐的运动方向与v0同向,石块落入筐中后随即与筐一起运动,试求:
(1)第一块石块刚落入筐中时石块与筐的共同速度v1;
(2)此人需向筐中仍入的石块数N。
7、有一内表面光滑的金属盒,底面长L=1.2m,质量为m1=0.5kg,放在水平面上,与水平面间的动摩擦因数μ=1/8,在盒内最右端放一个半径为r=0.1m的光滑金属球,质量为m2=0.5kg。现在盒最左端给盒施加一个水平冲量I =1.5N·s,如图所示(盒壁厚度,球与盒发生碰撞的时间和能量损失不计)。g=10m/s2,求:
(1)金属盒能在地面上运动多远?
(2)金属盒从开始运动到最后静止所经历的时间多长?
8、n个相同的木块,每块的质量都是m,放置在倾角为θ的斜面上,相邻两木块间的距离为L,最下端的木块距斜面底端也是L,木块与斜面间的动摩擦因数为μ,如图所示。在开始时刻,第一块木块以初速度v0沿斜面下滑,其余所有的木块都静止。由于第一个木块的下滑将依次引起一系列的碰撞,在每次发生碰撞后,发生碰撞的木块都粘在一起运动,直到最后第n个木块到达斜面底端时,刚好停在底端。求:
(1)第一次碰撞前第一个木块的动能Ek1;
(2)第一次碰撞时系统损失的机械能△E1与Ek1的比值;
(3)在整个过程中由于碰撞而损失的总机械能△E。
答案
1、(1)设子弹的初速度为v0,射入木块后两者的共同速度为v,以子弹和木块为系统,由动量守恒定律,有: v=
此过程系统所增加的内能为:
(2)设子弹以的速度刚好能够射穿材料相同、厚度为的另一木块。则对子弹和木块组成的系统,由动量守恒定律有:
此过程系统所损耗的机械能为:
由功能关系有:
故: 于是: 所以能射穿此木块。
2、设每次投掷时铅球相对车的速度为u,前一种方式投出一个球后,车速为,由动量守恒定律得:
投出第二个球后,车速为,由动量守恒定律得:
后一种方式投出球后,车速为,由动量守恒定律得:
故前后两次投掷铅球后小车获得的速度之比为:
3、(1)子弹打入木块以及木块运动的整个过程中,子弹和两木块组成的系统动量守恒,当弹簧压缩到最短时,A、B的速度相等,设为,则:
(2)子弹打入木块A的过程中,子弹和木块组成的系统动量守恒,设二者的共同速度为,则:
,
当弹簧达到最大长度时两木块速度相等,由动量守恒定律得:
从子弹射入木块A到两者具有共同速度以后的运动过程中,系统机械能守恒,故:
弹簧的最大长度为:
4、设小车被挡板挡住时,物体离开小车的水平速度为,从抛出点到落地点时间为,抛出点到落地点的高度为,则机械能守恒有: (1)
由平抛运动规律有: (2)
撤去挡板后,物体离开小车时车速大小为,物体速为,则由机械能守恒有:
(3)
由动量守恒有: (4)
由平抛运动规律有: (h不变,t不变) (5)
由(1)(3)(4)得:
由(2)式有,将、、代入(5)式得:
5、子弹射入小球前后,由动量守恒定律得: (1)
子弹射入小球后,小球上摆的高时小球的运动符合题意,设小球上摆的高度正好为,由机械能守恒得: (2)
由(1)(2)式得:
故,当时,小球在竖直平面内运动,绳不会松驰。
子弹射入小球后,若小球恰好能摆到2L的高度,则小球在竖直平面内做圆运动。设小球到达畅通高点时的速度为,则有: (3)
由机械能守恒得: (4)
由(1)(3)(4)得:
故当时,小球在竖直平面内做圆周运动,绳也不会松驰。
6、(1)设第一块石块扔入箩筐后,筐开始运动的速度为,由动量守恒定律有:
① ②
(2)第二块石块扔入箩筐时,由动量守恒定律有:
③ 由②③式得: ④
当第n个石块扔入筐时,筐的速度为: ⑤
若箩筐具有速度后恰能摆到A处,此时筐上升的高度为,由机械能守恒定律得:
⑥ ⑦
解⑤⑥⑦式得:
7、(1)由冲量的作用,,金属盒所受的摩擦力为:
,设它能在地面上滑行S(m),则由动能定理得:
解得:
(2)当盒前进时与球发生碰撞,设碰前盒的速度为,碰后的速度为,球碰后的速度为,则对盒用动能定理得: 解得:
由碰撞过程动量守恒和能量守恒有:
联立以上三式得:。同时,当球与盒再次碰撞时,球静止,盒以的速度前进,,所以不会再与球碰撞,则盒运动的时间可由动量定理求得:
解得:
在盒与球两次碰撞之间还有一段时间为小球在运动,
则金属盒从开始运动到最后静止所经历的时间为:
8、(1)依题意,最后一个木块停在斜面底端,表明木块除碰撞以外其它时间内所受合外力与运动方向相反,木块沿斜面做匀减速运动,设其加速度大小为,方向沿斜面向上,则:
①
第一次碰撞前第一个木块的动能为: ②
①式代入②式得: ③
(2)1、2两木块碰撞过程中动量守恒,有: ④ ⑤
上述过程中损失的机械能为: ⑥
解得: ⑦
由①式可知木块下滑的加速度与木块质量无关,从第1个木块开始下滑的整个过程中,除每一次碰撞的瞬间外,下滑加速度均为,方向沿斜面向上;在整个过程中,第n个木块运动距离为L,第n-1个木块运动的距离为2L,……第1个木块运动距离为nL,除碰撞瞬间外各木块克服合外力做功为:
⑧
整个过程中,各次碰撞损失的总机械能为: ⑨
由①⑧⑨式得:
同课章节目录
