2.3相反数课件（20张PPT)

２.５

２.５
1

1
每对数均为一正一负，只有＿＿＿＿不同．
符号
3

3
（1）－2.5与＋2.5，（2）＋1与－1，（3）＋3与－3
请同学们并观察下面每一组数中的两个数有什么相同点和不同点?
相反数的概念是什么？
观察这两个数，有什么相同和不同？
数字相同
符号不同
像1和-1、2.5和-2.5…这样只有符号不同的两个数叫做互为相反数。如 1是-1的相反数，-1是1的相反数。
规定：0的相反数是0。
你还能举出其它的相反数吗？
相 反 数
像1和-1、2.5和-2.5…这样符号不同数字相同的两个数叫做互为相反数。
分别写出下列数的相反数。
+11.2 , 7 , 0 , － 3 , － 100
例1：
解： +11.2 的相反数是－11.2 ,

7 的相反数是－7 ,
0 的相反数是 0 ,
－3 的相反数是 3 ,
－ 100 的相反数是 100 。
练 一 练
二、判断改错：
（1） 符号不同的两个数叫做相反数。（ ）
（2） 零的相反数是它本身。 （ ）
（3） 正数的相反数一定是负数。 （ ）
（4） －8是相反数。 （ ）
正数的相反数是（ ）数

负数的相反数是（ ）数

0的相反数是（ ）
负
正
想一想：
0
-4 -3 –2 –1 0 1 2 3 4
2
2
4
4
.
.
.
.
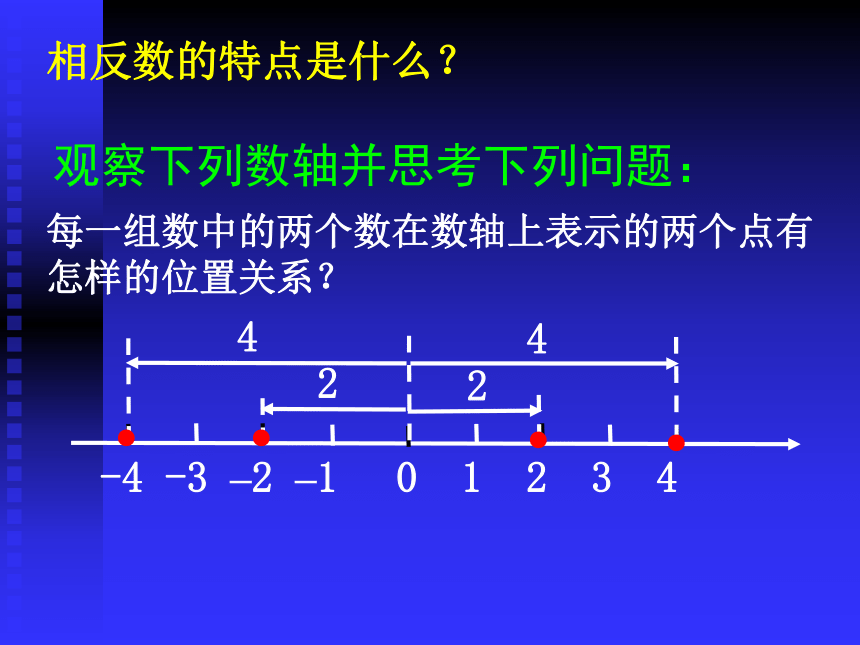
观察下列数轴并思考下列问题：
每一组数中的两个数在数轴上表示的两个点有怎样的位置关系？
相反数的特点是什么？
－2.5与＋2.5，＋1与－1，＋3与－3
．
．
＋２.５
－２.５
．
．
＋１
－１
．
．
每一对数在数轴上的对应点位于原点的两侧，且到原点的距离相等．
－3
+3
1、两个相反数在数轴上的对应点位于原点两侧，且到原点的距离相等
相反数的特点是什么？
2、两个相反数之和为（ ），之商为（ ）
0
-1
我们通常在一个数的前面加一个“—”号表示这个数的相反数，例如-4、 +5.5的相反数分别为：
-(-4)= , -(+5.5)= ，- 0 = .
例2：化简下列各数
⑴ -（+5）
⑵ +（-3）
⑶ +（+2）
⑷ -（-6）
同样，在一个数前面添上“+”号，表示这个数本身.例如
+(-4)=-4，+(+12)=12， +0 = 0.
=-5
=-3
=+2
=+6
=2
=6
正号可以省略不写
求相反数
4
-5.5
0
例 说出下列各式的意义并化简符号
（1）-（+3） （2）+（-4）
解 （1） -（+3）表示+3的相反数
所以 -（+3）=-3
（2）+（- 4）表示- 4的本身
所以+（- 4）= - 4
结论：要化简符号，首先要弄清意义。
例3：先说出下列式子的意义，再化简符号。

（1）－（ －7. 3 ) ( 2 ) －( + 5 )

( 3 ) +(－ 7 )


解：（1）－（－7.3 )表示－7.3的相反数，
∴－（－7.3 ) = 7.3
（2）－( + 5 )表示+ 5的相反数，
∴－( + 5 ) = - 5
要化简符号，首先要弄清意义。
（3）+( - 7 )表示-7的本身，
∴+( -7 ) = - 7

解：原式=-10
解：原式=-0.5
解：原式=3
解：原式=20
结论：要化简符号，首先要弄清意义。
结论：同号得正，异号得负
1、 ７是＿＿的相反数；
－（－７） 也是＿＿＿的相反数．
在一个数的前面添上“－”号表示原来这个数的相反数．
在一个数的前面添上“＋”号表示这个数本身．
－ 7
－7
求相反数中的有趣发现:
结论：－（－７） =7 ．
2、 a的相反数是＿＿ , 或者说－a的相反数是＿＿ ；
－a 的相反数又可表示为＿＿＿ ．
－ (－ a)
－a
结论：－（－a） = a ．.
a
2 、化解下列各数：
–（+10） ； ② +（ – 0.15）；
③ +（ + 3 ） ； ④ – ( –128 ) ;
解：① –（+10）= –10 ；
② +（ – 0.15）= – 0.15；
③ +（ + 3 ）= 3 ；
④ – ( –128 ) = 128 ;
我们一起来议一议：
小丸子说：一个数的相反数一定小于它本身.你认同她的说法吗？
同学们说：正数的相反数小于它本身；
　 负数的相反数大于它本身；
　 零的相反数是零．
1：先说出下列式子的意义，再化简符号。
（1） －（ －7. 3 ) ( 2 ) －( + 5 )
( 3 ) － ( + 2 . 8 ) ( 4 ) －(－2004)
多重符号的化简
偶正——奇负
练习： 化简下列各式:
(1) -(+3)= (2) – (-10)=
(3) –(+6.1)= (4) – (-7.8)=
(5) – [- (- 5) ] = (6) - [- (+5) ] =
(7) + [- (-5) ] = (8) + [- (+5) ] =

结果 (1) – 3, (2) +10, (3) - 6.1, (4) +7.8
(5) – 5, (6) + 5, (7) + 5 , (8) – 5 .
课本P21:习题2.3 第 1、2、3 、4 题
自我小结：1、相反数的概念
2、相反数的特点
3、化简符号的方法
导学案P5: 第 6题