2.6有理数的加法课件(31张PPT)
文档属性
| 名称 | 2.6有理数的加法课件(31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-25 16:58:56 | ||
图片预览







文档简介
一、温故知新、引入课题
问题:
小明在一条东西向上午跑道上,先走了20米,又走了30米,能否确定他现在的位于原来位置的哪个方向,与原来位置相距多少米?
试验:
因为这个问题涉及到方向,不妨规定向东为正,向西为负。
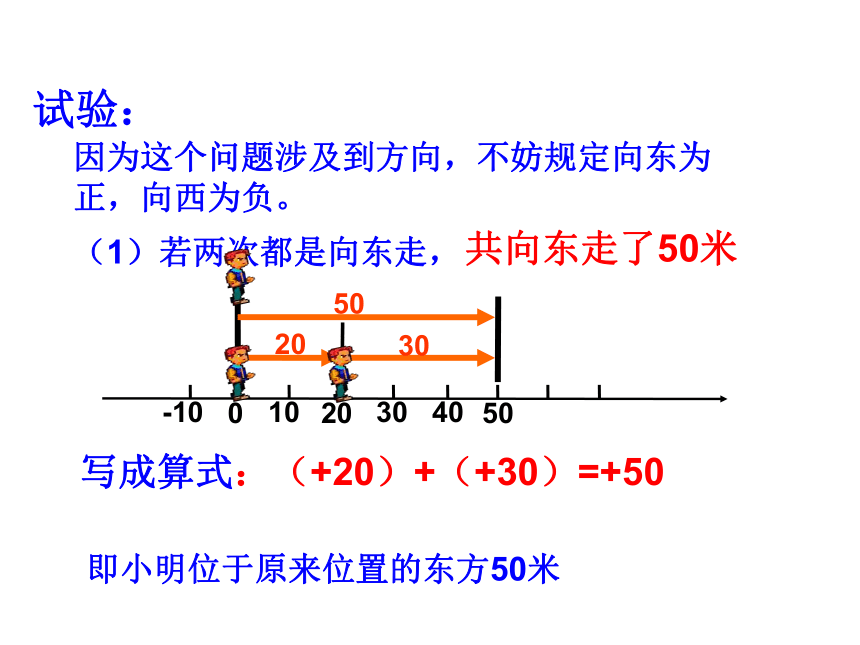
(1)若两次都是向东走,
10
30
40
30
50
-10
0
20
20
50
写成算式:(+20)+(+30)=+50
即小明位于原来位置的东方50米
共向东走了50米
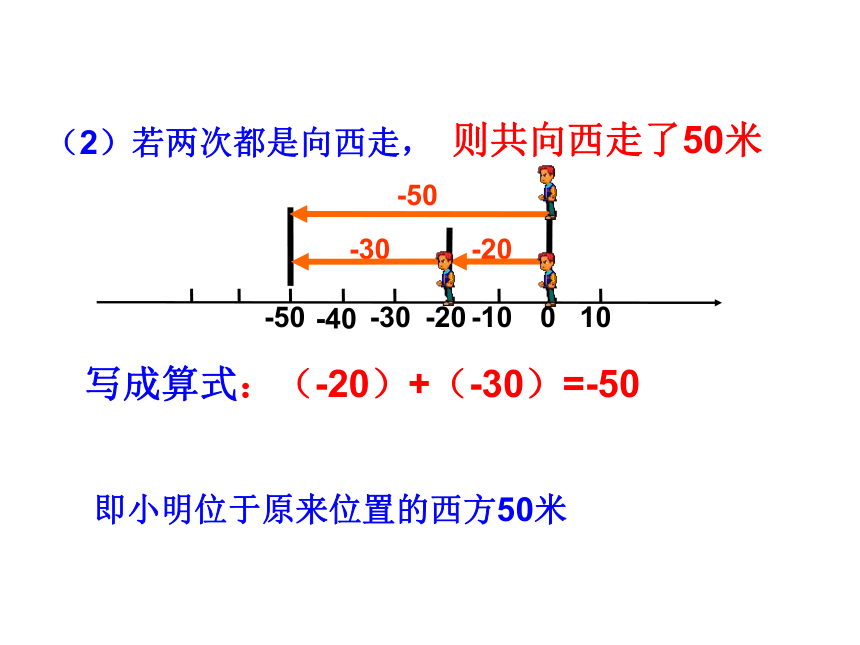
(2)若两次都是向西走,
10
-30
-40
-30
-50
-10
0
-20
-20
-50
写成算式:(-20)+(-30)=-50
即小明位于原来位置的西方50米
则共向西走了50米
同号两数相加,取与加数相同的符号,并把绝对值相加.
同正取正,绝对值相加
同负取负,绝对值相加
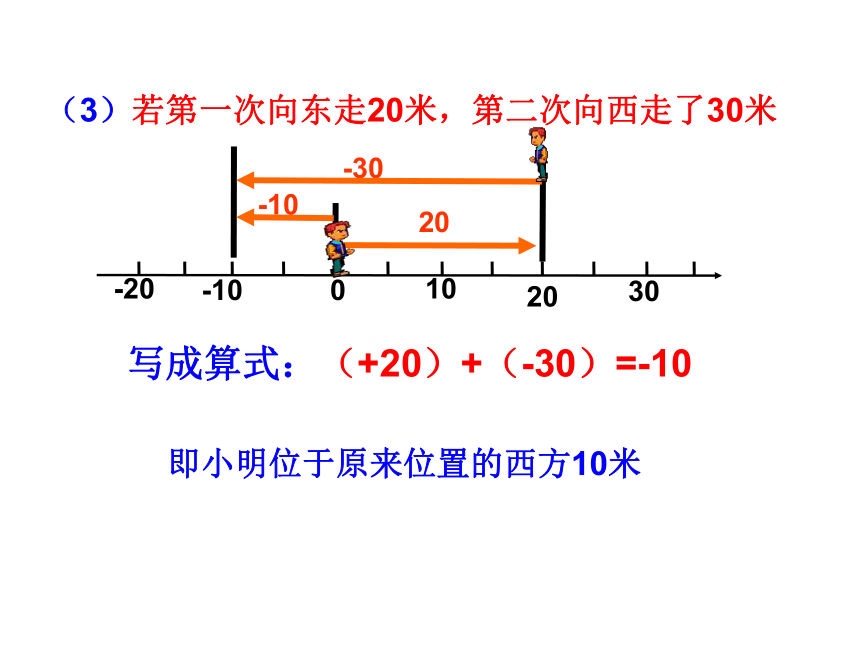
(3)若第一次向东走20米,第二次向西走了30米
10
30
-30
-20
-10
0
20
20
-10
写成算式:(+20)+(-30)=-10
即小明位于原来位置的西方10米
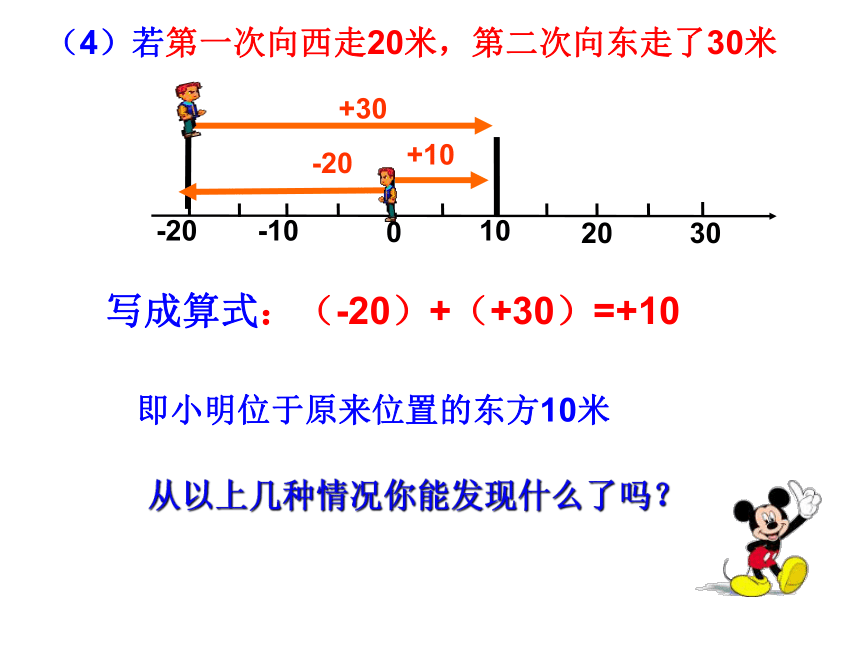
(4)若第一次向西走20米,第二次向东走了30米
10
30
-20
+30
-10
0
20
-20
+10
写成算式:(-20)+(+30)=+10
即小明位于原来位置的东方10米
从以上几种情况你能发现什么了吗?
从以上两个算式你能从中发现什么?
绝对值不等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
异号两数相加:负大取负,绝对值大减小.
异号两数相加:正大取正,绝对值大减小.
让我们再试几次:
(+4)+(+3)= (-5)+(-7)=
(+6)+(-8)= (-3)+(+5)=
-12
+7
-2
+2
同号两数相加,
取相同的符号,并把绝对值相加。
绝对值不等的异号两数相加,
取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
二、??得出法则,揭示内涵
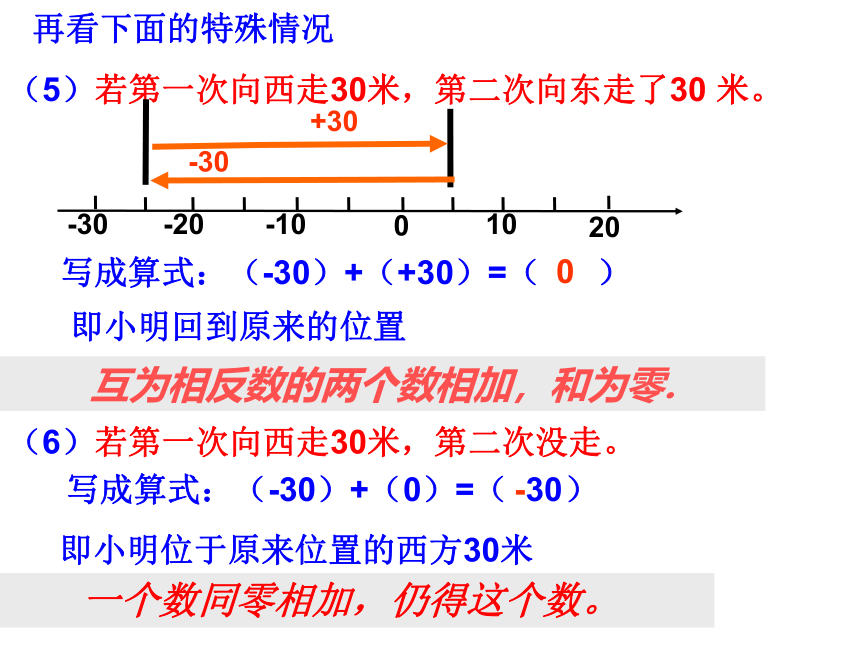
再看下面的特殊情况
(5)若第一次向西走30米,第二次向东走了30 米。
+30
-30
写成算式:(-30)+(+30)=( )
0
(6)若第一次向西走30米,第二次没走。
即小明回到原来的位置
写成算式:(-30)+(0)=( )
-30
即小明位于原来位置的西方30米
互为相反数的两个数相加,和为零.
一个数同零相加,仍得这个数。
通过以上探索,你来观察一下,在两个有理数相加的过程中“和的符号”怎样确定?“和的绝对值”怎样确定?
有理数的加法法则
一、同号两数相加:
二、绝对值不等的异号两数相加:
三、互为相反数的两个数相加:
四、一个数同零相加:
取与加数相同的符号,并把绝对值相加.
取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
得零.
仍得这个数.
同号相加一边倒
? 异号相加大减小”
? 符号跟着大的跑
注意:一个有理数由符号和绝对值两部分组成,进行加法运算时,应注意确定和的符号和绝对值.
即要先定符号,
再定绝对值
绝对值不等的异号两数相加,分步思考:
①确定和的符号;
②确定和的绝对值,写出所得和;
③相反数相加直接得出零。
注意:
有理数的加法运算
例1:
1、(-4)+(-5 )
=-( ) (取相同的符号)
=-(4 + 5) (把绝对值相加)
=- 9
(同号两数相加)
2、( -6) + 2
(绝对值不相等的异号两数相加)
(取绝对值较大的加数符号)
(用较大的绝对值减去较小的绝对值)
=-( )
=- 4
=-(6 – 2 )
应用
(1) (-3)+(-9)
(2)( )+(+ )
(3) 0 +( -0﹒1 )
例2: 计算
解:(1)原式 =-(3+9)
=-12
(2)原式=-( - )
=-
(3) 原式= -0﹒1
5
7
12
_
+
1
0
13
+
_
看谁先学会!
阅读下列解题过程,是否有错?若有错,请说出错的原因。
计算 (+3)+(-5)
解:(+3)+(-5)=2
正确解法(+3)+(-5)
=-(5-3)
=-2
错解分析:本题计算忽略了“先定符号,后定绝对值”的顺序,因此平时解题时,一定要遵循法则等
异号两数相加(取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值)
三、强化法则,深入理解
发挥你的聪明才智,若回答问题正确,则可打开一扇门.
1.(口答)计算:
(+5)+(+3) (-5)+(-3)
(-11)+(-6)
=+8
=-8
=-17
(+5)+(-3) ; (-5)+(+3) ;
(-11)+(+6)
=+2
=- 2
=- 5
变换题型了
2:在括号里填上适当的符号,使下列式子成立:
(1)(__5)+( ___5)=0
(2)( __7 )+(- 5)=-12
_
_
+
(3)(-10)+( __11)=+1
(4)(__2.5)+(__2.5 )=-5
_
+
_
打开这一扇门,你会有所发现
解:
(1) (+2)+(-11)
=
-(11-2)
=-9
(2)(+20)+(+12)
=
+(20+12)
=+32
(3) ( )+( )
=
=
-( + )
(4) ( -3.2 )+4.3
=
+(4.3-3.2)
=+0.9
四、例题示范,初步运用
1、(+4)+(+3)= 2、(+4)+(-3)=
3、(+3)+(-10)= 4、(-5)+(+7)=
5、(-6)+(+2) = 6、(-4)+(-11)=
7、(+30)+(-30)= 8、(-2)+(+2)=
9、 0+(-23)= 10、(+16)+0=
+7
+1
-7
+2
-4
-15
0
0
-23
+16
五、分层练习,形成能力
计算
1、4+3= 2、4-3=
3、3-10= 4、-5+7=
5、-6+2= 6、-4-11=
7、30-30= 8、-2+2=
9、0-23= 10、16+0=
+7
+1
-7
+2
-4
-15
0
0
-23
+16
分层练习,形成能力
计算
+
18+8
+26
+
16-9
+7
-
9+5
-14
加数
加数 和的组成
和
符号 绝对值
-12 3 - 12-3 -9
18 8
-9 16
-9 -5
填空
1.( )+(-3)= -8 2.( ) +(-3)= 8
3.( -3)+( )= -1 4.( - 3)+( )= 0
-5
+11
+2
+3
判断
1.两数和一定大于每一个加数.( )
2.两数和一定大于两数绝对值的和.( )
3.两数和一定小于两数绝对值的和.( )
1.两数相加,如果和比每个加数都小,那么这两个数( )
A、 同为负数 B、异号 C、同为正数
D、零或负数
2、如果两数的和为正数,那么一定有( )
A、一个加数为正,另一个加数为0
B、这两个加数都是正数
C、一个为正数,另一个为负数,且正数的绝对值较大
D、至少有一个加数为正数
A
D
3、两数相加,如果和比其中一个加数大,而比另一个加数小,那么这两个数( )
A、同为负数 B、异号
C、同为正数 D、有一个是0
4、下面哪个数集中减法总是可以进行的( )
A、自然数集合 B、有理数集合
C、正数集合 D、负数集合
B
B
这节课的收获是……
这节课我们从实例出发,经过比较、归纳,得出了有理数加法的法则.今后我们经常要用类似的思想方法研究其他问题。
应用有理数加法法则进行计算时,要同时注意确定“和”的符号,计算“和”的绝对值两件事。?
用“<”或“>”填空:
(1)如果a>0,b>0,那么a+b 0。
(2)如果a>0,b<0,且︱a ︱> ︱b︱,那么a+b 0。
(3)如果a<0,a+b>0,那么︱a ︱ ︱b︱
>
>
<
(b>0)
课本P31:练习第1、2、3题
P34习题2.6第 1、2 题
导学案P11: 第4题
P12: 第1、2、3题
问题:
小明在一条东西向上午跑道上,先走了20米,又走了30米,能否确定他现在的位于原来位置的哪个方向,与原来位置相距多少米?
试验:
因为这个问题涉及到方向,不妨规定向东为正,向西为负。
(1)若两次都是向东走,
10
30
40
30
50
-10
0
20
20
50
写成算式:(+20)+(+30)=+50
即小明位于原来位置的东方50米
共向东走了50米
(2)若两次都是向西走,
10
-30
-40
-30
-50
-10
0
-20
-20
-50
写成算式:(-20)+(-30)=-50
即小明位于原来位置的西方50米
则共向西走了50米
同号两数相加,取与加数相同的符号,并把绝对值相加.
同正取正,绝对值相加
同负取负,绝对值相加
(3)若第一次向东走20米,第二次向西走了30米
10
30
-30
-20
-10
0
20
20
-10
写成算式:(+20)+(-30)=-10
即小明位于原来位置的西方10米
(4)若第一次向西走20米,第二次向东走了30米
10
30
-20
+30
-10
0
20
-20
+10
写成算式:(-20)+(+30)=+10
即小明位于原来位置的东方10米
从以上几种情况你能发现什么了吗?
从以上两个算式你能从中发现什么?
绝对值不等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
异号两数相加:负大取负,绝对值大减小.
异号两数相加:正大取正,绝对值大减小.
让我们再试几次:
(+4)+(+3)= (-5)+(-7)=
(+6)+(-8)= (-3)+(+5)=
-12
+7
-2
+2
同号两数相加,
取相同的符号,并把绝对值相加。
绝对值不等的异号两数相加,
取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
二、??得出法则,揭示内涵
再看下面的特殊情况
(5)若第一次向西走30米,第二次向东走了30 米。
+30
-30
写成算式:(-30)+(+30)=( )
0
(6)若第一次向西走30米,第二次没走。
即小明回到原来的位置
写成算式:(-30)+(0)=( )
-30
即小明位于原来位置的西方30米
互为相反数的两个数相加,和为零.
一个数同零相加,仍得这个数。
通过以上探索,你来观察一下,在两个有理数相加的过程中“和的符号”怎样确定?“和的绝对值”怎样确定?
有理数的加法法则
一、同号两数相加:
二、绝对值不等的异号两数相加:
三、互为相反数的两个数相加:
四、一个数同零相加:
取与加数相同的符号,并把绝对值相加.
取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
得零.
仍得这个数.
同号相加一边倒
? 异号相加大减小”
? 符号跟着大的跑
注意:一个有理数由符号和绝对值两部分组成,进行加法运算时,应注意确定和的符号和绝对值.
即要先定符号,
再定绝对值
绝对值不等的异号两数相加,分步思考:
①确定和的符号;
②确定和的绝对值,写出所得和;
③相反数相加直接得出零。
注意:
有理数的加法运算
例1:
1、(-4)+(-5 )
=-( ) (取相同的符号)
=-(4 + 5) (把绝对值相加)
=- 9
(同号两数相加)
2、( -6) + 2
(绝对值不相等的异号两数相加)
(取绝对值较大的加数符号)
(用较大的绝对值减去较小的绝对值)
=-( )
=- 4
=-(6 – 2 )
应用
(1) (-3)+(-9)
(2)( )+(+ )
(3) 0 +( -0﹒1 )
例2: 计算
解:(1)原式 =-(3+9)
=-12
(2)原式=-( - )
=-
(3) 原式= -0﹒1
5
7
12
_
+
1
0
13
+
_
看谁先学会!
阅读下列解题过程,是否有错?若有错,请说出错的原因。
计算 (+3)+(-5)
解:(+3)+(-5)=2
正确解法(+3)+(-5)
=-(5-3)
=-2
错解分析:本题计算忽略了“先定符号,后定绝对值”的顺序,因此平时解题时,一定要遵循法则等
异号两数相加(取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值)
三、强化法则,深入理解
发挥你的聪明才智,若回答问题正确,则可打开一扇门.
1.(口答)计算:
(+5)+(+3) (-5)+(-3)
(-11)+(-6)
=+8
=-8
=-17
(+5)+(-3) ; (-5)+(+3) ;
(-11)+(+6)
=+2
=- 2
=- 5
变换题型了
2:在括号里填上适当的符号,使下列式子成立:
(1)(__5)+( ___5)=0
(2)( __7 )+(- 5)=-12
_
_
+
(3)(-10)+( __11)=+1
(4)(__2.5)+(__2.5 )=-5
_
+
_
打开这一扇门,你会有所发现
解:
(1) (+2)+(-11)
=
-(11-2)
=-9
(2)(+20)+(+12)
=
+(20+12)
=+32
(3) ( )+( )
=
=
-( + )
(4) ( -3.2 )+4.3
=
+(4.3-3.2)
=+0.9
四、例题示范,初步运用
1、(+4)+(+3)= 2、(+4)+(-3)=
3、(+3)+(-10)= 4、(-5)+(+7)=
5、(-6)+(+2) = 6、(-4)+(-11)=
7、(+30)+(-30)= 8、(-2)+(+2)=
9、 0+(-23)= 10、(+16)+0=
+7
+1
-7
+2
-4
-15
0
0
-23
+16
五、分层练习,形成能力
计算
1、4+3= 2、4-3=
3、3-10= 4、-5+7=
5、-6+2= 6、-4-11=
7、30-30= 8、-2+2=
9、0-23= 10、16+0=
+7
+1
-7
+2
-4
-15
0
0
-23
+16
分层练习,形成能力
计算
+
18+8
+26
+
16-9
+7
-
9+5
-14
加数
加数 和的组成
和
符号 绝对值
-12 3 - 12-3 -9
18 8
-9 16
-9 -5
填空
1.( )+(-3)= -8 2.( ) +(-3)= 8
3.( -3)+( )= -1 4.( - 3)+( )= 0
-5
+11
+2
+3
判断
1.两数和一定大于每一个加数.( )
2.两数和一定大于两数绝对值的和.( )
3.两数和一定小于两数绝对值的和.( )
1.两数相加,如果和比每个加数都小,那么这两个数( )
A、 同为负数 B、异号 C、同为正数
D、零或负数
2、如果两数的和为正数,那么一定有( )
A、一个加数为正,另一个加数为0
B、这两个加数都是正数
C、一个为正数,另一个为负数,且正数的绝对值较大
D、至少有一个加数为正数
A
D
3、两数相加,如果和比其中一个加数大,而比另一个加数小,那么这两个数( )
A、同为负数 B、异号
C、同为正数 D、有一个是0
4、下面哪个数集中减法总是可以进行的( )
A、自然数集合 B、有理数集合
C、正数集合 D、负数集合
B
B
这节课的收获是……
这节课我们从实例出发,经过比较、归纳,得出了有理数加法的法则.今后我们经常要用类似的思想方法研究其他问题。
应用有理数加法法则进行计算时,要同时注意确定“和”的符号,计算“和”的绝对值两件事。?
用“<”或“>”填空:
(1)如果a>0,b>0,那么a+b 0。
(2)如果a>0,b<0,且︱a ︱> ︱b︱,那么a+b 0。
(3)如果a<0,a+b>0,那么︱a ︱ ︱b︱
>
>
<
(b>0)
课本P31:练习第1、2、3题
P34习题2.6第 1、2 题
导学案P11: 第4题
P12: 第1、2、3题
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
