人教版数学五上梯形的面积课件(共16张)
图片预览





文档简介
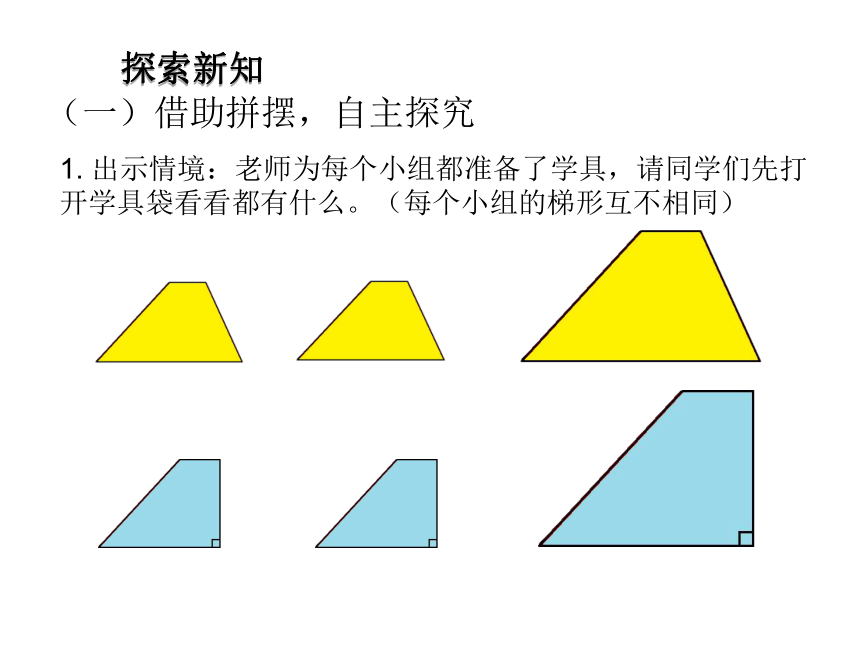
课件16张PPT。梯形的面积人教版五年级上册第一单元《小数乘法》学习目标1.使学生在理解的基础上探索并掌握梯形面积计算公式的推导过程,能利用公式求梯形的面积。2.进一步体会利用转化的方法解决问题。通过动手操作、观察和比较,发展学生的空间观念,培养学生观察操作、推理的能力以及解决问题的能力。3.在探索学习活动中,培养探索意识、合作意识和创新意识,并获得积极的、成功的情感体验。(一)出示情境:情景导入(二)提出问题:过渡:这节课我们就来一起学习梯形的面积。问题:回忆一下,我们是怎样推导出三角形面积的计算公式的?预设:我们用两个完全一样的三角形拼成了一个平行四边形,或者把一个三角形用割补法拼成一个平行四边形;然后找到新旧图形之间整体和局部的联系;最后推导出三角形的面积公式。车窗玻璃的形状是梯形!怎样求出它的面积呢?你能用学过的方法推导出梯形的面积计算公式吗?探索新知(一)借助拼摆,自主探究1. 出示情境:老师为每个小组都准备了学具,请同学们先打开学具袋看看都有什么。(每个小组的梯形互不相同)探索新知(一)借助拼摆,自主探究2. 提出问题:你能根据已有的经验,借助手中的学具推导出梯形的面积计算公式吗?3. 提出要求:请同学们两人一组,借助你们手中的梯形纸
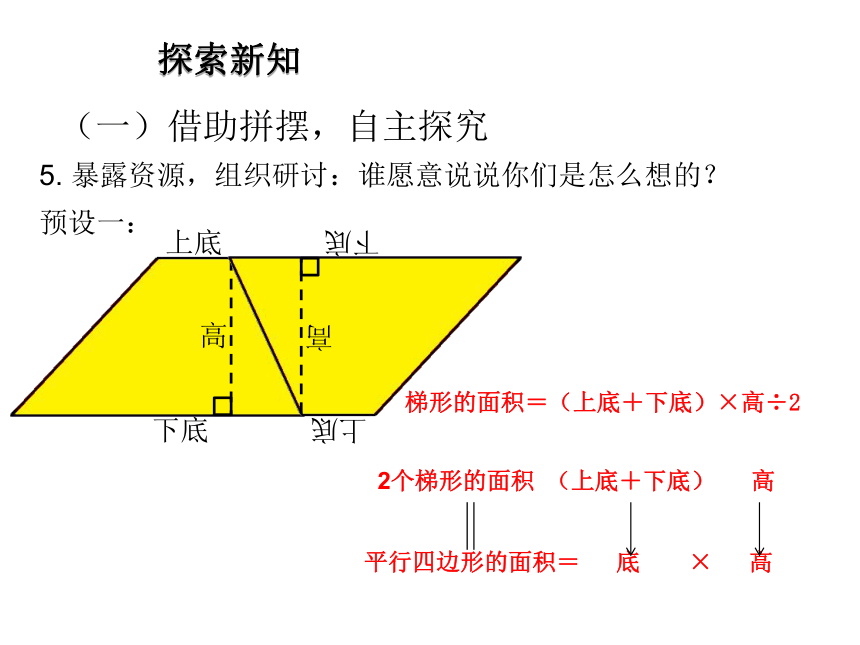
片,可以拼一拼,画一画,剪一剪,看看能不能把梯形转化成我们学习过的图形,并找到转化前后图形间的联系,把你找到的联系在纸上写一写,让别人一眼就能看出你是如何推导出梯形面积计算方法的,看哪组的方法最多,学具不够用可以找老师领取。4. 学生自主探究,教师巡视搜集资源。探索新知(一)借助拼摆,自主探究5. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?预设一:平行四边形的面积= 底 × 高 2个梯形的面积 (上底+下底) 高 梯形的面积=(上底+下底)×高÷2探索新知(一)借助拼摆,自主探究预设二:平行四边形的面积= 底 × 高 2个梯形的面积 (上底+下底) 高 梯形的面积=(上底+下底)×高÷25. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?探索新知(一)借助拼摆,自主探究6. 总结概括,提升认识:通过同学们刚才的汇报,我们发现只要是两个完全一样的梯形,我们就能把它们拼成一个平行四边形或长方形,充分论证了梯形的面积=(上底+下底)×高÷2。过渡:刚才我还发现有的同学只用一个梯形就推导出了梯形的面积计算公式,你们想看看吗?探索新知(一)借助拼摆,自主探究7. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?预设一:梯形的面积=小三角形的面积+大三角形的面积=上底×高÷2+下底×高÷2=(上底+下底)×高÷2探索新知(一)借助拼摆,自主探究预设二:梯形的面积=平行四边形的面积+三角形的面积=上底×高+(下底-上底)×高÷2=(上底+下底)×高÷27. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?探索新知(一)借助拼摆,自主探究预设四:平行四边形的面积 = 底 × 高 梯形的面积 (上底+下底)÷2 高 梯形的面积= (上底+下底) ×高÷2上底下底高7. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?探索新知(一)借助拼摆,自主探究8. 总结概括,提升认识:通过同学们刚才的汇报,我们发现只要是运用相应的方法把梯形分割或割补成学过的图形,然后找到相应的新旧图形的联系,充分论证了梯形的面积=(上底+下底)×高÷2。9. 如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,那么梯形的面积计算公式是:
S=(a+b)h÷2探索新知我国三峡水电站大坝的横截面的一部分是梯形(如下
图),求它的面积。S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
=10530(m2)探索新知一辆汽车侧面的两块玻璃的形状是梯形(如下图),
它们的面积分别是多少?S=(a+b)h÷2
=(40+71)×40÷2
=111×40÷2
=2220(cm2)S=(a+b)h÷2
=(45+65)×40÷2
=110×40÷2
=2200(cm2)学以致用课堂小结
片,可以拼一拼,画一画,剪一剪,看看能不能把梯形转化成我们学习过的图形,并找到转化前后图形间的联系,把你找到的联系在纸上写一写,让别人一眼就能看出你是如何推导出梯形面积计算方法的,看哪组的方法最多,学具不够用可以找老师领取。4. 学生自主探究,教师巡视搜集资源。探索新知(一)借助拼摆,自主探究5. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?预设一:平行四边形的面积= 底 × 高 2个梯形的面积 (上底+下底) 高 梯形的面积=(上底+下底)×高÷2探索新知(一)借助拼摆,自主探究预设二:平行四边形的面积= 底 × 高 2个梯形的面积 (上底+下底) 高 梯形的面积=(上底+下底)×高÷25. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?探索新知(一)借助拼摆,自主探究6. 总结概括,提升认识:通过同学们刚才的汇报,我们发现只要是两个完全一样的梯形,我们就能把它们拼成一个平行四边形或长方形,充分论证了梯形的面积=(上底+下底)×高÷2。过渡:刚才我还发现有的同学只用一个梯形就推导出了梯形的面积计算公式,你们想看看吗?探索新知(一)借助拼摆,自主探究7. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?预设一:梯形的面积=小三角形的面积+大三角形的面积=上底×高÷2+下底×高÷2=(上底+下底)×高÷2探索新知(一)借助拼摆,自主探究预设二:梯形的面积=平行四边形的面积+三角形的面积=上底×高+(下底-上底)×高÷2=(上底+下底)×高÷27. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?探索新知(一)借助拼摆,自主探究预设四:平行四边形的面积 = 底 × 高 梯形的面积 (上底+下底)÷2 高 梯形的面积= (上底+下底) ×高÷2上底下底高7. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?探索新知(一)借助拼摆,自主探究8. 总结概括,提升认识:通过同学们刚才的汇报,我们发现只要是运用相应的方法把梯形分割或割补成学过的图形,然后找到相应的新旧图形的联系,充分论证了梯形的面积=(上底+下底)×高÷2。9. 如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,那么梯形的面积计算公式是:
S=(a+b)h÷2探索新知我国三峡水电站大坝的横截面的一部分是梯形(如下
图),求它的面积。S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
=10530(m2)探索新知一辆汽车侧面的两块玻璃的形状是梯形(如下图),
它们的面积分别是多少?S=(a+b)h÷2
=(40+71)×40÷2
=111×40÷2
=2220(cm2)S=(a+b)h÷2
=(45+65)×40÷2
=110×40÷2
=2200(cm2)学以致用课堂小结
