3.2 平行线分线段成比例课时作业

中小学教育资源及组卷应用平台


3.2 平行线分线段成比例课时作业
学校:___________姓名：___________班级：___________考号：___________
　
一．选择题（共8小题）
1．如图，DE∥FG∥BC，若DB=4FB，则EG与GC的关系是（　　）

A．EG=4GC B．EG=3GC C．EG=GC D．EG=2GC
2．如图，已知直线a∥b∥c，直线m交直线a，b，c于点A，B，C，直线n交直线a，b，c于点D，E，F，若=，则=（　　）

A． B． C． D．1
3．如图，在△ABC中，点D在AB上，BD=2AD，DE∥BC交AC于E，则下列结论不正确的是（　　）

A．BC=3DE B．=
C．△ADE∽△ABC D．S△ADE=S△ABC
4．如图，在△ABC中，DE∥BC，AD=6，DB=3，AE=4，则EC的长为（　　）

A．1 B．2 C．3 D．4
5．如图，直线l1∥l2∥l3，直线AC分别交l1，l2，l3于点A，B，C，直线DF分别交l1，l2，l3于点D，E，F，AC与DF相交于点G，且AG=2，GB=1，BC=5，则的值为（　　）

A． B．2 C． D．
6．如图，在△ABC中，DE∥BC，若=，则=（　　）

A． B． C． D．
7．如图，AG：GD=4：1，BD：DC=2：3，则AE：EC的值是（　　）

A．3：2 B．4：3 C．6：5 D．8：5
8．如图，AD∥BC，AD⊥AB，点A，B在y轴上，CD与x轴交于点E（2，0），且AD=DE，BC=2CE，则BD与x轴交点F的横坐标为（　　）

A． B． C． D．
　
二．填空题（共7小题）
9．如图，直线l1∥l2∥l3，直线AC交l1，l2，l3于点A，B，C；直线DF交l1，l2，l3于点D，E，F，已知=，则=　 　．

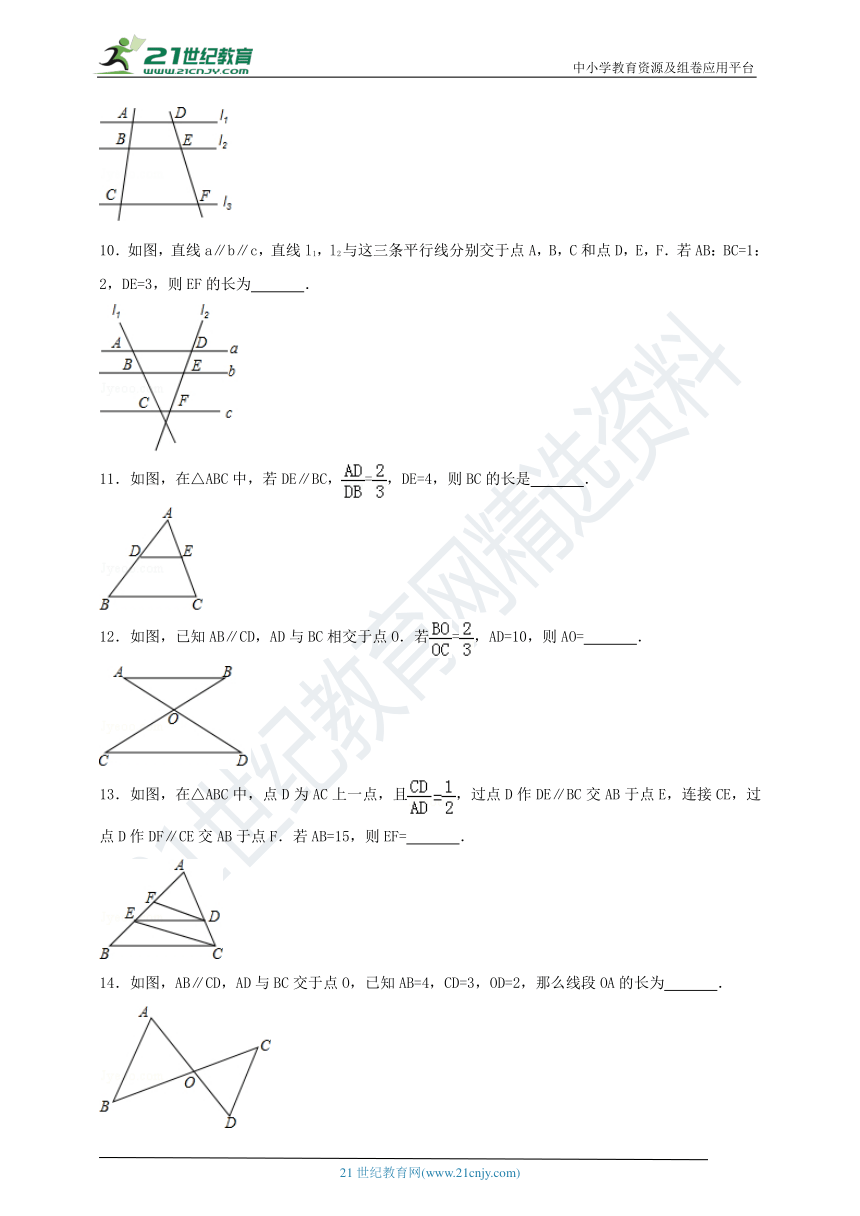
10．如图，直线a∥b∥c，直线l1，l2与这三条平行线分别交于点A，B，C和点D，E，F．若AB：BC=1：2，DE=3，则EF的长为　 　．

11．如图，在△ABC中，若DE∥BC，=，DE=4，则BC的长是　 　．

12．如图，已知AB∥CD，AD与BC相交于点O．若=，AD=10，则AO=　 　．

13．如图，在△ABC中，点D为AC上一点，且，过点D作DE∥BC交AB于点E，连接CE，过点D作DF∥CE交AB于点F．若AB=15，则EF=　 　．

14．如图，AB∥CD，AD与BC交于点O，已知AB=4，CD=3，OD=2，那么线段OA的长为　 　．

15．如图，△ABC中，点D、E分别在边AB、BC上，DE∥AC．若BD=4，DA=2，BE=3，则EC=　 　．

　
三．解答题（共6小题）
16．如图，在△ABC中，点D，E分别在边AB，AC上，若DE∥BC，AD=3，AB=5，求的值．

17．如图，在△ABC中，AB=AC，BE平分∠ABC，DE∥BC．
求证：DE=EC．

18．如图，在正方形ABCD中，E是AB的中点，连接CE，过B作BF⊥CE交AC于F．求证：CF=2FA．

19．已知：如图，在△ABC中，∠ACB的平分线CD交AB于D，过B作BE∥CD交AC的延长线于点E．
（1）求证：BC=CE；
（2）求证：．

20．如图，已知E是平行四边形ABCD中DA边的延长线上一点，且AE=AD，连接EC分别交AB，BE于点F、G．
（1）求证：BF=AF；
（2）若BD=12cm，求DG的长．

21．如图所示，在矩形ABCD中，AC、BD相交于点O，OE⊥BC于E，连接DE交OC于点F，作FG⊥BC于G．
（1）说明点G是线段BC的一个三等分点；
（2）请你依照上面的画法，在原图上画出BC的一个四等分点（保留作图痕迹，不必证明）．

　




参考答案与试题解析
　
一．选择题（共8小题）
1．【考点】平行线分线段成比例
【分析】根据平行线分线段成比例定理即可得到答案．
解：∵DE∥FG∥BC，DB=4FB，
∴．
故选：B．
【点评】此题主要考查平行线分线段成比例定理的理解及运用．根据平行线分线段成比例定理解答是解题的关键．
　
2．【考点】平行线分线段成比例
【分析】直接根据平行线分线段成比例定理求解．
解：∵a∥b∥c，
∴==．
故选：B．
【点评】本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．
　
3．【考点】平行线分线段成比例
【分析】根据平行线分线段成比例定理、相似三角形的性质解答即可．
解：∵BD=2AD，
∴AB=3AD，
∵DE∥BC，
∴==，
∴BC=3DE，A结论正确；
∵DE∥BC，
∴=，B结论正确；
∵DE∥BC，
∴△ADE∽△ABC，C结论正确；
∵DE∥BC，AB=3AD，
∴S△ADE=S△ABC，D结论错误，
故选：D．
【点评】本题考查的是平行线分线段成比例定理和相似三角形的性质，灵活运用平行线分线段成比例定理、掌握相似三角形的面积比等于相似比的平方是解题的关键．
　
4．【考点】平行线分线段成比例
【分析】根据平行线分线段成比例可得，代入计算即可解答．
解：∵DE∥BC，
∴，
即，
解得：EC=2，
故选：B．
【点评】本题主要考查平行线分线段成比例，掌握平行线分线段所得线段对应成比例是解题的关键．
　
5．【考点】平行线分线段成比例
【分析】根据平行线分线段成比例可得，代入计算，可求得答案．
解：∵AG=2，GB=1，
∴AB=AG+BG=3，
∵直线l1∥l2∥l3，
∴=，
故选：D．
【点评】本题主要考查平行线分线段成比例，掌握平行线分线段所得线段对应成比例是解题的关键．
　
6．【考点】平行线分线段成比例
【分析】直接利用平行线分线段成比例定理写出答案即可．
解：∵DE∥BC，
∴==，
故选：C．
【点评】本题考查了平行线分线段成比例定理，了解定理的内容是解答本题的关键，属于基础定义或定理，难度不大．
　
7．【考点】平行线分线段成比例
【分析】过点D作DF∥CA交BE于F，如图，利用平行线分线段成比例定理，由DF∥CE得到==，则CE=DF，由DF∥AE得到===，则AE=4DF，然后计算的值．
解：过点D作DF∥CA交BE于F，如图，
∵DF∥CE，
∴=，
而BD：DC=2：3，
∴=，则CE=DF，
∵DF∥AE，
∴=，
∵AG：GD=4：1，
∴=，则AE=4DF，
∴==．
故选：D．

【点评】本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．平行于三角形一边的直线截其他两边（或两边的延长线），所截得的三角形的三边与原三角形的三边对应成比例．
　
8．【考点】坐标与图形性质；平行线分线段成比例
【分析】如图，设OF=a，AD=DE=x，CE=y，则BC=2y，根据平行线分线段成比例可得xy=a（x+y），2xy=（2﹣a）（x+y），联立得到2a（x+y）=（2﹣a）（x+y）且x+y≠0，即2a=（2﹣a），解方程求得a，从而求解．
解：如图，设OF=a，AD=DE=x，CE=y，则BC=2y，
则==，
即=，
xy=a（x+y），
又∵=，即=，
2xy=（2﹣a）（x+y），
∴2a（x+y）=（2﹣a）（x+y）且x+y≠0，
∴2a=（2﹣a），
解得a=．
故点F的横坐标为．
故选：A．

【点评】考查了坐标与图形性质，平行线分线段成比例，关键是熟练掌握平行线分线段成比例的性质，注意方程思想的运用．
　
二．填空题（共7小题）
9．【考点】平行线分线段成比例
【分析】根据题意求出，根据平行线分线段成比例定理解答．
解：∵=，
∴=2，
∵l1∥l2∥l3，
∴==2，
故答案为：2．
【点评】本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键．
　
10．【考点】平行线分线段成比例
【分析】由a∥b∥c，可得=，由此即可解决问题．
解：∵a∥b∥c，
∴=，
∴=，
∴EF=6，
故答案为6．

【点评】本题考查平行线分线段成比例定理，解题的关键是正确应用平行线分线段成比例定理，属于中考常考题型．
　
11．【考点】平行线分线段成比例
【分析】因为DE∥BC，可利用平行线分线段成比例定理求出BC的长．
解：∵DE∥BC，
∴=，
又∵=，
∴=，
∴=，
∴BC=10cm．
故答案为：10cm．
【点评】本题考查了平行线分线段成比例定理，找出图中的比例关系是解题的关键．
　
12．【考点】平行线分线段成比例
【分析】根据平行线分线段成比例定理列出比例式，计算即可．
解：∵AB∥CD，
∴==，即=，
解得，AO=4，
故答案为：4．
【点评】本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键．
　
13．【考点】平行线分线段成比例
【分析】由DE与BC平行，由平行得比例求出AE的长，再由DF与CE平行，由平行得比例求出EF的长即可．
解：∵DE∥BC，
∴=，
∵=，
∴=，即=，
∵AB=15，
∴AE=10，
∵DF∥CE，
∴=，即=，
解得：AF=，
则EF=AE﹣AF=10﹣=，
故答案为：
【点评】此题考查了平行线分线段成比例，熟练掌握平行线分线段成比例性质是解本题的关键．
　
14．【考点】平行线分线段成比例
【分析】根据平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例得到OA：OD=AB：CD，然后利用比例性质计算OA的长．
解：∵AB∥CD，
∴OA：OD=AB：CD，即OA：2=4：3，
∴OA=．
故答案为．
【点评】本题考查了平行线分线段成比例：平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．
　
15．
【考点】平行线分线段成比例
【分析】根据平行线分线段成比例定理即可直接求解．
解：∵DE∥AC，
∴，
即，
解得：EC=．
故答案为：．
【点评】本题考查了平行线分线段成比例定理，理解定理内容是解题的关键．
　
三．解答题（共6小题）
16．【考点】平行线分线段成比例
【分析】根据平行线分线段成比例定理得出=，再根据AD=3，AB=5，即可得出答案．
解：∵DE∥BC，
∴=，
∵AD=3，AB=5，
∴=．
【点评】此题考查了平行线分线段成比例定理．此题难度不大，解题的关键是注意准确应用平行线分线段成比例定理与数形结合思想的应用．
　
17．【考点】JA：平行线的性质；等腰三角形的性质；平行线分线段成比例
【分析】由DE∥BC，可知=，由AB=AC，可知DB=EC，由角平分线及平行线的性质可知∠DEB=∠DBE．故DE=EC．
证明：∵DE∥BC，
∴=．
又∵AB=AC，
∴DB=EC．
∵DE∥BC，
∴∠DEB=∠EBC．
而∵∠DBE=∠EBC，
∴∠DEB=∠DBE．
∴DB=DE．
∴DE=EC．
【点评】本题主要考查等腰三角形的性质，综合利用了平行线的性质和角平分线的定义，是中学阶段的基本题目．
　
18．【考点】全等三角形的判定与性质；正方形的性质；平行线分线段成比例
【分析】延长BF交AD于G，根据正方形的性质得到∠ABG=∠BCE，可证△ABG≌△BCE，所以AG=BE，利用AG∥BC，可知FA：CF=AG：BC=1：2，所以CF=2FA．
证明：延长BF交AD于G，
∵四边形ABCD是正方形，
∴AB=BC=AD，∠DAB=∠ABC=90°，AD∥BC，
∴∠ABG+∠CBG=90°，
∵BF⊥CE，
∴∠CBG+∠BCE=90°，
∴∠ABG=∠BCE，
∴△ABG≌△BCE，
∴AG=BE，
∵BE=AB，
∴AG=AB=BC，
∴AG：BC=1：2，
∵AD∥BC，
∴FA：CF=AG：BC=1：2，
∴CF=2FA．

【点评】主要考查了正方形的性质和全等三角形的判定以及相似三角形中成比例线段的运用．根据正方形的性质找到相等的边和角来证明三角形全等，并利用相似比求线段之间的数量关系是解题的关键．
　
19．【考点】等腰三角形的性质；平行线分线段成比例
【分析】（1）根据CD平分∠ACB，可知∠ACD=∠BCD；由BE∥CD，可求出△BCE是等腰三角形，故BC=CE；
（2）根据平行线的性质，及BC=CE可得出结论．
证明：（1）∵CD平分∠ACB，
∴∠ACD=∠BCD．
又∵BE∥CD，
∴∠CBE=∠BCD，∠CEB=∠ACD．
∵∠ACD=∠BCD，
∴∠CBE=∠CEB．
故△BCE是等腰三角形，BC=CE．

（2）∵BE∥CD，根据平行线分线段成比例定理可得=，
又∵BC=CE，∴=．
【点评】本题主要考查了等腰三角形的判定及性质和角平分线定理．
　
20．【考点】全等三角形的判定与性质；平行四边形的性质；平行线分线段成比例
【分析】（1）欲证BF=AF，只需证△AEF≌△BCF即可．
（2）DG是BD的一部分，要找DG与BD的关系，可找DG与BG的关系，由BC∥DE可以得出．
（1）证明：∵平行四边形ABCD，
∴AD∥BC，AD=BC．
∴∠E=∠BCF．
∵AE=AD，
∴AE=BC．
∵∠AFE=∠BFC，
∴△AEF≌△BCF．
∴BF=AF．

（2）解：∵BC∥DE，
∴BC：DE=BG：DG．
∵DE=2BC，
∴DG=2BG．
∴DG=BD．
∵BD=12，
∴DG=8．
【点评】本题考查的是利用平行四边形的性质结合三角形全等，及平行线分线段成比例定理来解决有关线段长度的问题．
　
21．【考点】矩形的性质；平行线分线段成比例
【分析】（1）根据矩形对角线的性质可以判断E为BC的二等分点，再由OE∥CD，OE=CD，得出EG=GC，从而得出GC=CE=BC．
（2）依题意，根据平行线分线段成比例定理直接在图中作图即可．
解：（1）∵OE⊥BC，CD⊥BC，
∴OE∥CD．
∵△OEF∽△CDF，
∴．
∵四边形ABCD是矩形，
∴AD∥BC．
∴．
∴G是BC的三等分点；

（2）依题意画图如右．

【点评】本题考查平行线分线段成比例定理，需要根据平行找准对应关系，要和相似三角形对应边成比例加以区别．
　





















































21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)