3.4 相似三角形的判定与性质(2)课时作业
文档属性
| 名称 | 3.4 相似三角形的判定与性质(2)课时作业 |

|
|
| 格式 | zip | ||
| 文件大小 | 256.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-26 00:00:00 | ||
图片预览




文档简介
3.4 相似三角形的判定与性质(2)课时作业
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题)
1.如图,AB∥CD,AE∥FD,则图中的相似三角形共有( )
A.2对 B.4对 C.6对 D.8对
2.如图,在△ABC中,已知EF∥BC,=,四边形BCFE的面积为8,则△ABC的面积等于( )
A.9 B.10 C.12 D.13
3.如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则的值为( )
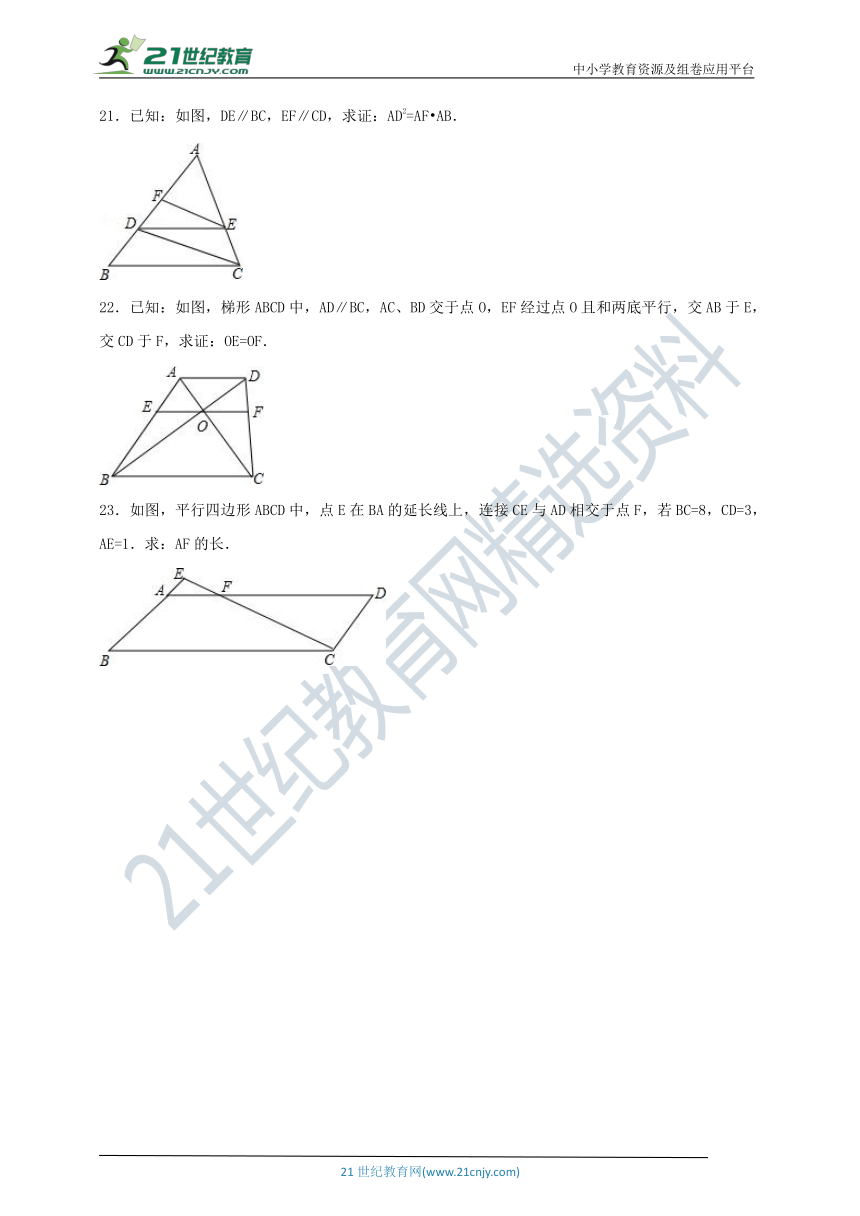
A.1 B. C.1 D.
4.如图,在菱形ABCD中,点E为边AD的中点,且∠ABC=60°,AB=6,BE交AC于点F,则AF=( )
A.1 B.2 C.2.5 D.3
5.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.3:4 B.9:16 C.9:1 D.3:1
6.如图,在?ABCD中,点E在边AD上,射线CE、BA交于点F,下列等式成立的是( )
A. B. C. D.
7.如图,在平行四边形ABCD中,点E在边DC上,联结AE并延长交BC的延长线于点F,若AD=3CF,那么下列结论中正确的是( )
A.FC:FB=1:3 B.CE:CD=1:3 C.CE:AB=1:4 D.AE:AF=1:2.
8.如图,已知DE∥BC,CD和BE相交于点O,S△DOE:S△COB=9:16,则DE:BC为( )
A.2:3 B.3:4 C.9:16 D.1:2
9.如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,DE:EC=2:3,则S△DEF:S△ABF=( )
A.2:3 B.4:9 C.2:5 D.4:25
10.在△ABC中,边BC=6,高AD=4,正方形EFGH的顶点E、F在边BC上,顶点H、G分别在边AB和AC上,那么这个正方形的边长等于( )
A.3 B.2.5 C.2.4 D.2
二.填空题(共6小题)
11.如图,AB∥CD∥EF,则图中相似的三角形有 对.
12.如图所示,点E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形: .
13.如图,△ABC中,D、E分别在AB、AC上,DE∥BC,AD:AB=2:3,则△ADE与△ABC的面积之比为 .
14.如图,在?ABCD中,AC是一条对角线,EF∥BC,且EF与AB相交于点E,与AC相交于点F,3AE=2EB,连接DF.若S△AEF=1,则S△ADF的值为 .
15.如图,在△ABC中,DE∥BC,=,则= .
16.如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF:GF=1:2,那么矩形DEFG的周长是 .
三.解答题(共7小题)
17.已知如图:DE∥BC,并分别交AB、AC于点D、E.求证:△ADE∽△ABC.
18.如图,已知△ABC中,四边形DEGF为正方形,D、E在线段AC、BC上,F、G在AB上,如果S△ADF=S△CDE=1,S△BEG=3,求△ABC的面积.
19.如图,已知梯形上下底边的长分别为36和60,高为32,这个梯形两腰的延长线的交点到两底的距离分别是多少?
20.如图,在△ABC中,DE∥BC,AD=2cm,BD=3cm.
(1)求的值.
(2)若梯形BCED的面积为63cm2,求△ADE的面积.
21.已知:如图,DE∥BC,EF∥CD,求证:AD2=AF?AB.
22.已知:如图,梯形ABCD中,AD∥BC,AC、BD交于点O,EF经过点O且和两底平行,交AB于E,交CD于F,求证:OE=OF.
23.如图,平行四边形ABCD中,点E在BA的延长线上,连接CE与AD相交于点F,若BC=8,CD=3,AE=1.求:AF的长.
参考答案与试题解析
一.选择题(共10小题)
1.【考点】相似三角形的判定
【分析】根据AB∥CD,AE∥FD可以判定图中所有的三角形相似,故从4个中任意选2个均相似,即可解题.
解:AB∥CD,AE∥FD
∴图中4个三角形均相似,
从4个中任选2个均相似,
故有C42对相似三角形,故有6对,
故选:C.
【点评】本题考查了相似三角形的判定,考查了相似三角形的传递性,本题中求证4个三角形均相似是解题的关键.
2.【考点】相似三角形的判定与性质
【分析】由题意可证△AEF∽△ABC,可得=()2=,即可求△ABC的面积.
解:∵
∴=
∵EF∥BC
∴△AEF∽△ABC
∴=()2=
∴S△ABC=9S△AEF
∵S四边形BCFE=S△ABC﹣S△AEF=8S△AEF=8
∴S△AEF=1
∴S△ABC=9
故选:A.
【点评】本题考查了相似三角形的性质和判定,熟练运用相似三角形的性质解决问题是本题关键.
3.【考点】相似三角形的判定与性质
【分析】由DE∥BC可得出△ADE∽△ABC,利用相似三角形的性质结合S△ADE=S四边形BCED,可得出=,结合BD=AB﹣AD即可求出的值,此题得解.
解:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴()2=.
∵S△ADE=S四边形BCED,
∴=,
∴===﹣1.
故选:C.
【点评】本题考查了相似三角形的判定与性质,牢记相似三角形的面积比等于相似比的平方是解题的关键.
4.【考点】菱形的性质;相似三角形的判定与性质
【分析】由题意可证△ABC是等边三角形,可得AC=AB=BC=6,由AD∥BC,可得CF=2AF,即可求AF的长.
解:∵四边形ABCD是菱形
∴AD∥BC,AD=AB=BC=6且∠ABC=60°
∴△ABC是等边三角形
∴AC=6
∵点E为边AD的中点
∴AE=DE=3
∵AD∥BC
∴△AEF∽△BFC
∴==
∴CF=2AF
∵AC=CF+AF=3AF=6
∴AF=2
故选:B.
【点评】本题考查相似三角形的判定和性质,菱形的性质,关键是灵活运用这些性质解决问题.
5.【考点】平行四边形的性质;相似三角形的判定与性质
【分析】可证明△DFE∽△BFA,根据相似三角形的面积之比等于相似比的平方即可得出答案.
解:∵四边形ABCD为平行四边形,
∴DC∥AB,
∴△DFE∽△BFA,
∵DE:EC=3:1,
∴DE:DC=3:4,
∴DE:AB=3:4,
∴S△DFE:S△BFA=9:16.
故选:B.
【点评】本题考查了平行四边形的性质以及相似三角形的判定和性质,注:相似三角形的面积之比等于相似比的平方.
6.【考点】平行四边形的性质;相似三角形的判定与性质
【分析】根据平行四边形的性质及平行线分线段成比例的性质即可得出答案.
解:A、∵△AEF∽△EDC,∴,错误;
B、∵△AEF∽△EDC,∴,错误;
C、∵△AEF∽△EDC,∴,∵AE∥BC,∴,∴,正确;
D、∵△AEF∽△EDC,∴,错误;
故选:C.
【点评】本题主要考查了相似三角形的判定和性质,关键是根据平行四边形的性质及平行线分线段成比例的性质解答.
7.【考点】平行四边形的性质;相似三角形的判定与性质
【分析】由四边形ABCD是平行四边形得AD∥BC,证△ECF∽△ADE,进而判断即可.
解:∵在平行四边形ABCD中,
∴AD∥BC,
∴△ECF∽△ADE,
∵AD=3CF,
A、FC:FB=1:4,错误;
B、CE:CD=1:4,错误;
C、CE:AB=1:4,正确;
D、AE:AF=3:4.错误;
故选:C.
【点评】本题主要考查相似三角形的判定与性质及平行四边形的性质,熟练掌握相似三角形的判定和性质是解题的关键.
8.【考点】相似三角形的判定与性质
【分析】根据相似三角形的面积比即可求出答案.
解:∵DE∥BC,
∴△DOE∽△BOC,
∴=()2
∴
故选:B.
【点评】本题考查相似三角形的性质,解题的关键是熟练运用相似三角形的性质,本题属于基础题型.
9.【考点】平行四边形的性质;相似三角形的判定与性质
【分析】根据已知可得到相似三角形,从而可得到其相似比,再根据相似三角形的面积比等于相似比的平方就可得到答案.
解:如图,∵四边形ABCD是平行四边形,
∴DC∥AB,CD=AB.
∴△DFE∽△BFA,
∴S△DEF:S△ABF=DE2:AB2,
∵DE:EC=2:3,
∴DE:DC=DE:AB=2:5,
∴S△DEF:S△ABF=4:25
故选:D.
【点评】本题考查的是相似三角形的判定与性质及平行四边形的性质,熟知相似三角形边长的比等于相似比,面积的比等于相似比的平方是解答此题的关键.
10.【考点】正方形的性质;相似三角形的判定与性质
【分析】利用正方形的性质可知EH∥BC,再利用平行线分线段成比例定理的推论可得△AHE∽△ACB,利用相似三角形的性质可得比例线段,利用比例线段可求正方形的边长
解:∵四边形EFMN是正方形,
∴EH∥BC,EH=EF,
∴△AEH∽△ABC,
又∵AD⊥BC,
∴AD⊥BC,EH=EF=MD,
∴=,
设EH=x,则AM=3﹣x,
∴=,
解得:x=2.4,
∴EH=2.4.
答:这个正方形的边长为2.4.
故选:C.
【点评】本题考查了相似三角形的判定和性质、正方形的性质和平行线分线段成比例定理,是各地中考考查相似三角形常见题型.
二.填空题(共6小题)
11.【考点】平行线的性质;相似三角形的判定
【分析】本题主要掌握相似三角形的定义,根据已知条件识别相似的三角形.
解:∵AB∥CD∥EF,
∴△DCE∽△BAE,△DCA∽△FEA,△BDA∽△DFE,
∴共有3对相似三角形;
故答案为:3
【点评】此题主要考查学生对相似三角形的判定方法的掌握情况,关键是根据已知条件识别相似的三角形.
12.【考点】平行四边形的性质;相似三角形的判定
【分析】利用平行四边形的性质得到AD∥CE,则根据相似三角形的判定方法可判断△ADF∽△ECF.
解:∵四边形ABCD为平行四边形,
∴AD∥CE,
∴△ADF∽△ECF.
故答案为△ADF∽△ECF.
【点评】本题考查了相似三角形的判定:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;有两组角对应相等的两个三角形相似.也考查了平行四边形的性质.
13.【考点】相似三角形的判定与性质
【分析】由DE与BC平行,得到两对同位角相等,利用两对角相等的三角形相似得到三角形ADE与三角形ABC相似,利用相似三角形的面积之比等于相似比的平方即可得到结果.
解:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴S△ADE:S△ABC=(AD:AB)2=4:9,
故答案为:4:9.
【点评】此题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.
14.【考点】平行四边形的性质;相似三角形的判定与性质
【分析】由3AE=2EB可设AE=2a、BE=3a,根据EF∥BC得=()2=,结合S△AEF=1知S△ADC=S△ABC=,再由==知=,继而根据S△ADF=S△ADC可得答案.
解:∵3AE=2EB,
∴可设AE=2a、BE=3a,
∵EF∥BC,
∴△AEF∽△ABC,
∴=()2=()2=,
∵S△AEF=1,
∴S△ABC=,
∵四边形ABCD是平行四边形,
∴S△ADC=S△ABC=,
∵EF∥BC,
∴===,
∴==,
∴S△ADF=S△ADC=×=,
故答案为:.
【点评】本题主要考查相似三角形的判定与性质,解题的关键是掌握相似三角形的判定及性质、平行线分线段成比例定理及平行四边形的性质.
15.【考点】相似三角形的判定与性质
【分析】由DE∥BC可得出∠ADE=∠B、∠AED=∠C,进而可得出△ADE∽△ABC,根据相似三角形的性质可得出的值.
解:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴==.
故答案为:.
【点评】本题考查了相似三角形的判定与性质,利用相似三角形的判定定理证出△ADE∽△ABC是解题的关键
16.【考点】矩形的性质;相似三角形的判定与性质
【分析】根据矩形的性质可得出GF∥BC,进而可得出△AGF∽△ABC,设EF=x,则GF=2x,根据相似三角形的性质即可得出关于x的一元一次方程,解之即可得出x的值,再利用矩形的周长公式即可求出矩形DEFG的周长.
解:设EF=x,则GF=2x,
根据题意得:=,
解得:x=3,
矩形DEFG的周长为(2x+x)×2=6x=18.
故答案为:18.
【点评】本题考查了相似三角形的判定与性质、矩形的性质以及解一元一次方程,根据相似三角形的性质列出关于x的一元一次方程是解题的关键.
三.解答题(共7小题)
17.【考点】相似三角形的判定
【分析】先根据平行线的性质可得∠ADE=∠B,∠AED=∠C,然后根据有两组角对应相等的两个三角形相似即可得到结论.
证明:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC.
【点评】本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了平行线的性质.
18.【考点】LE:正方形的性质;相似三角形的判定与性质
【分析】过C作CH⊥AB于H,交DE于M,设AF=a,正方形DFGE的边长为b,CM=h,由于S△CDE=bh=1,S△AFD=ab=1,于是得到a=h,CH=h+b=a+b,根据S△BEG=BG?b=3,得到GB=3a,于是求出S△ABC=AB?CH=(a+b+3a)(a+b)=b2+5,由于ab=2,于是求得2a2+b2=b2,通过化简即可得到结论.
解:过C作CH⊥AB于H,交DE于M,设AF=a,正方形DFGE的边长为b,CM=h,
∴S△CDE=bh=1,S△AFD=ab=1,
∴a=h,∴CH=h+b=a+b,
∵S△BEG=BG?b=3,
∴GB=3a,
∴S△ABC=AB?CH=(a+b+3a)(a+b)=b2+5,
∵ab=2,
∴2a2+b2=b2,
∴b=2a,
∴bb=2,
∴b2=4,
∴S△ABC=b2+5=9.
【点评】本题考查了三角形的面积直角三角形的性质,正方形的性质,熟练掌握各性质定理是解题的关键.
19.【考点】梯形;相似三角形的判定与性质
【分析】设两腰的延长线交于点E,过E作EG⊥CD,交AB于点F,交CD于点G,则FG=32,由条件可得△EAB∽△EDC,可得=,且EG=EF+FG,代入可求得EF,进一步可求得EG.
解:如图,设两腰的延长线交于点E,过E作EG⊥CD,交AB于点F,交CD于点G,则EF⊥AB,FG=32,
∵AB∥CD,
∴△EAB∽△EDC,
∴=,且EG=EF+FG=EF+32,
∴=,
解得EF=48,
则EG=48+32=80,
即梯形两腰的延长线的交点到两底的距离分别为48和32.
【点评】本题主要考查相似三角形的判定和性质,掌握相似三角形对应高的比等于相似比是解题的关键,注意方程思想的应用.
20.【考点】相似三角形的判定与性质
【分析】(1)由DE∥BC,利用平行线分线段成比例定理的推论,可知△ADE∽△ABC,再利用比例线段可求的值;
(2)由DE∥BC,可证△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方,即可得到结论.
解:(1)∵DE∥BC,
∴△ADE∽△ABC,
∴,
∵AD=2cm,BD=3cm,
∴=;
(2)∵DE∥BC,
∴△ADE∽△ABC,
∴=()2=,
∵梯形BCED的面积为63cm2,
∴S△ADE=12cm2.
【点评】本题考查了相似三角形的判定与性质.关键是利用平行线得相似,利用相似三角形的面积的性质求解.
21.【考点】相似三角形的判定与性质
【分析】由DE∥BC,EF∥CD,可得△ADE∽△ABC,△AFE∽△ADC,然后由相似三角形的对应边成比例,证得结论.
证明:∵DE∥BC,EF∥CD,
∴△ADE∽△ABC,△AFE∽△ADC,
∴AD:AB=AE:AC,AF:AD=AE:AC,
∴AD:AB=AF:AD,
∴AD2=AF?AB.
【点评】此题考查了相似三角形的判定与性质.注意掌握相似三角形的对应边成比例.
22.【考点】梯形;相似三角形的判定与性质
【分析】由梯形ABCD中,AD∥BC,EF经过点O且和两底平行,易得△AOD∽△COB,△AEO∽△ABC,△DOF∽△DBC,然后由相似三角形的对应边成比例,证得结论.
证明:∵梯形ABCD中,AD∥BC,
∴△AOD∽△COB,
∴OA:OC=OA:OB,
∴OA:AC=OD:BD,
∵EF∥BC,
∴△AEO∽△ABC,△DOF∽△DBC,
∴OE:BC=OA:AC,OF:BC=OD:BD,
∴OE:BC=OF:BC,
∴OE=OF.
【点评】此题考查了相似三角形的判定与性质.注意证得△AOD∽△COB,△AEO∽△ABC,△DOF∽△DBC是关键.
23.【考点】平行四边形的性质;相似三角形的判定与性质
【分析】由四边形ABCD是平行四边形,得到AD∥BC,AB=CD=3,推出△EAF∽△EBC,然后根据相似三角形的性质列比例式,即可得到结论.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=3,
∴△EAF∽△EBC,
∴,
∵BC=8,CD=3,AE=1,
∴BE=4,
∴,
∴AF=2.
【点评】本题考查了相似三角形的判定和性质,平行四边形的性质,熟练掌握相似三角形的判定和性质是解题的关键.
第1页(共17页)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
