2.7.1有理数的乘法课件

《义务教育教科书》
鲁教版（五四制）
2.7 有理数的乘法（第一课时）
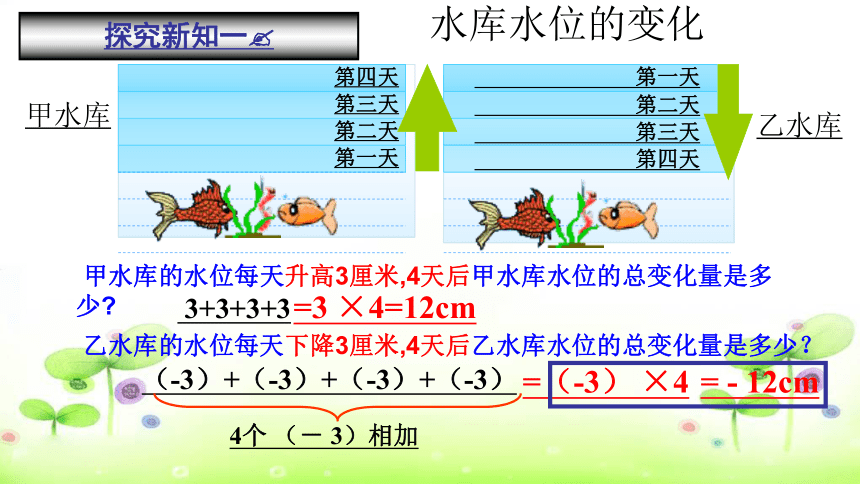
水库水位的变化







第一天







第二天
第三天
第四天
第一天
第二天
第三天
第四天
甲水库
乙水库
甲水库的水位每天升高3厘米,4天后甲水库水位的总变化量是多少?
探究新知一?
3+3+3+3
（-3）+（-3）+（-3）+（-3）
4个 （－ 3）相加
=（-3） ×4
= - 12cm
=3 ×4=12cm
乙水库的水位每天下降3厘米,4天后乙水库水位的总变化量是多少？
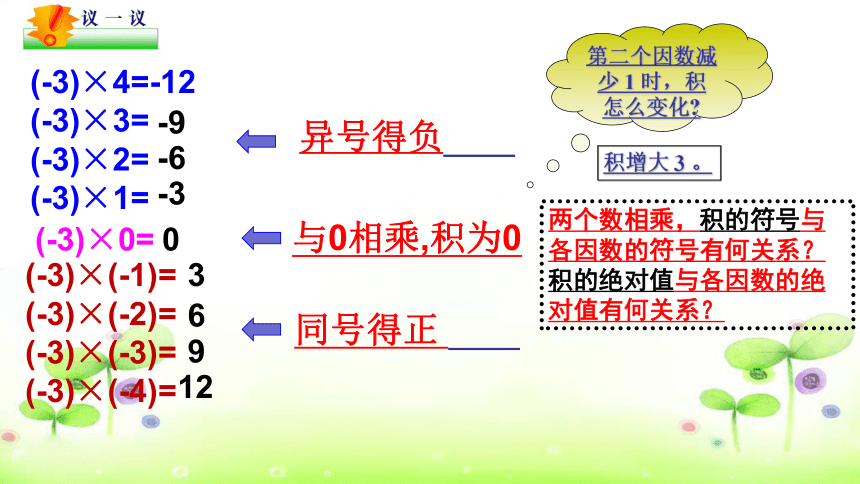
第二个因数减少 1 时，积 怎么变化?
积增大 3 。
(-3)×4=-12
(-3)×3=
(-3)×2=
(-3)×1=
(-3)×0=
(-3)×(-1)=
(-3)×(-2)=
(-3)×(-3)=
(-3)×(-4)=
-9
-6
0
-3
6
9
12
3
两个数相乘，积的符号与各因数的符号有何关系？积的绝对值与各因数的绝对值有何关系？
异号得负
同号得正
与0相乘,积为0
有理数的乘法法则
两数相乘，同号得 ，异号得 ，绝对值相乘；
任何数与0相乘,积仍为0.
正
负
归纳总结?
摸牌小游戏：
游戏规则：两人搭档，一人从四张牌中任选两张，利用出现的数字组成乘法算式，另一人完成剩下两张牌的计算.其他同学完成以上两个乘法算式.
例 题 解 析
例1 计算：
(1)
(2)
求解中的第一步是 ；
确定积的符号
第二步
是 ；
绝对值相乘
? 方法总结 ?
计算：
（1）（-4）×(+10) （2） 0×（-2014）
（3）（-5）×1 （4） 7×1
（5）（-12）×（-1） （6） 36×（-1）

（7）（- ）×（- ） （8）（-3）×（- ）

1
-1
大显身手?
（7）（- ）×（- ）=1 （8）（-3）×（- ）=1
如果两个有理数的乘积为1，那么称其中一个数是另一个数的倒数，也称这两个有理数互为倒数.
0没有倒数
判断：
摸牌小游戏：
(1)(－1)×2×3×4
(2)(－1)×(－2)×3×4
(3)(－1)×(－2)×(－3)×4
(4)(－1)×(－2)×(－3)×(－4)
(5)(－1)×(－2)×(－3)×(－4)×0
= - 24
= +24
= - 24
= 0
?探究新知二
= +24
计算下列各式：
它们的积的符号怎样确定？积的绝对值怎样确定？
几个不等于0的数相乘，积的符号
由 的个数决定.
当负因数有 个时，积的符号为 ；
当负因数有 个时，积的符号为 .
积的绝对值等于 。
负因数
奇数
负
偶数
正
各个因数的绝对值的积
(1)(－1)×2×3×4=-24
(2)(－1)×(－2)×3×4=24
(3)(－1)×(－2)×(－3)×4=-24
(4)(－1)×(－2)×(－3)×(－4)=24
几个数相乘，有一个因数为0时，积就为 .
? 应用反思 ?
如果我们把乘法法则推广到三个或三个以上有理数相乘，可“一次性地”先定号再绝对值相乘.
归纳总结?
(5)(－1)×(－2)×(－3)×(－4)×0=0
0
通过本课的学习，你学到了什么知识？
1.（1）（-8）×
思维大舞台?
A层.
B层.
1. 用正负数表示气温的变化量，上升为正，下降为负，登山队攀登一座山峰，每登高1km气温的变化量为－6 0C，攀登3km后，气温有什么变化？
2.点A、B在数轴上的位置如图所示，则A与B所表示的两个数的积（???）.?
A.?一定是正数????????B.?一定是负数?
C.?等于零????????????D.?正、负数不确定
拓展提高：


1.某地气象统计资料表明，高度每增加1000m，气温就降低大约6℃。现在地面气温是37 ℃ ，问10000m高空的气温大约是多少？
C层：
问题解决：
2.计算：
谢 谢！
恳请各位评委老师批评指正！