22.1.5 用待定系数法求二次函数的解析式同步练习(含答案)
文档属性
| 名称 | 22.1.5 用待定系数法求二次函数的解析式同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 49.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-27 20:02:54 | ||
图片预览

文档简介
用待定系数法求二次函数的解析式 同步练习题
基础题
知识点1 利用“三点式”求二次函数解析式
1.已知二次函数y=-x2+bx+c的图象经过A(2,0),B(0,-6)两点,则这个二次函数的解析式为______________________.
2.若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
x
-7
-6
-5
-4
-3
-2
y
-27
-13
-3
3
5
3
则此二次函数的解析式为____________________.
3.已知二次函数y=ax2+bx+c,当x=0时,y=1;当x=-1时,y=6;当x=1时,y=0.求这个二次函数的解析式.
4.如图,抛物线y=x2+bx+c与x轴交于A,B两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标.
知识点2 利用“顶点式”求二次函数解析式
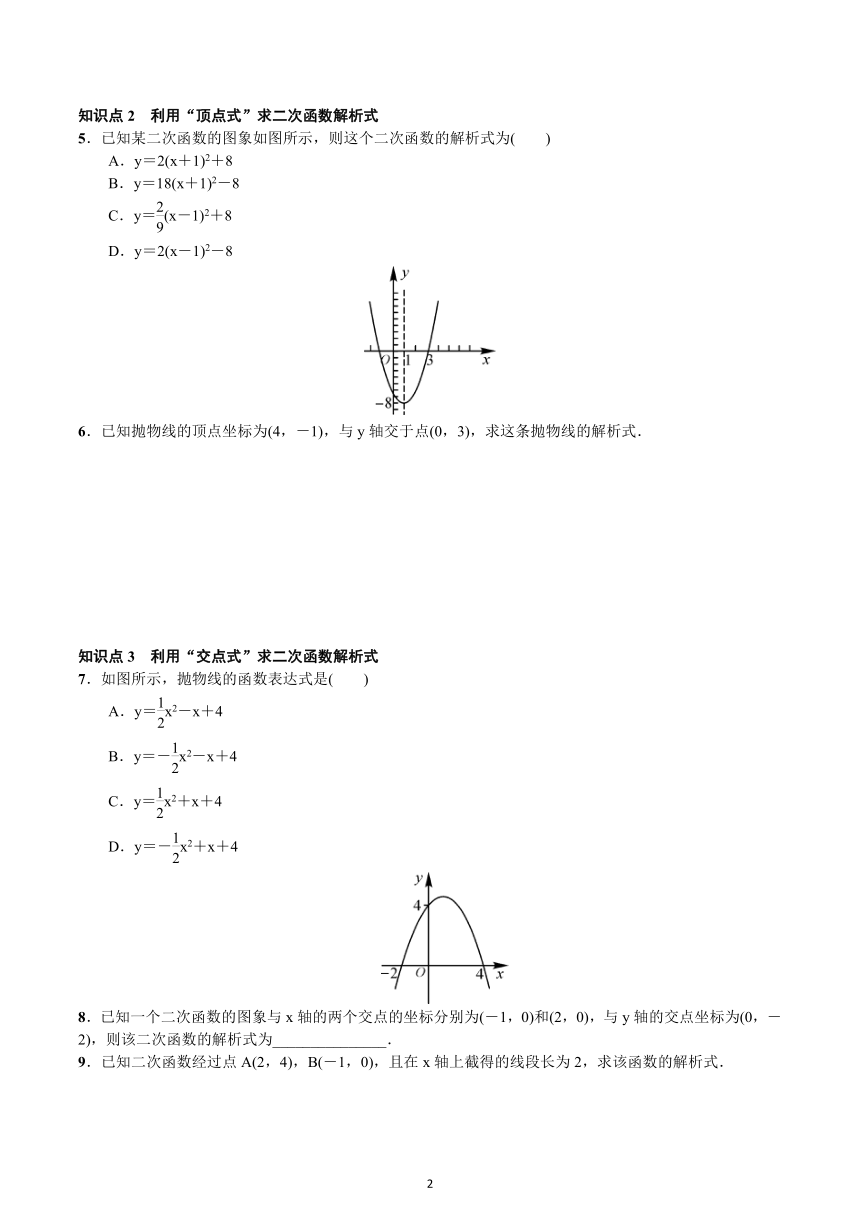
5.已知某二次函数的图象如图所示,则这个二次函数的解析式为( )
A.y=2(x+1)2+8
B.y=18(x+1)2-8
C.y=(x-1)2+8
D.y=2(x-1)2-8
6.已知抛物线的顶点坐标为(4,-1),与y轴交于点(0,3),求这条抛物线的解析式.
知识点3 利用“交点式”求二次函数解析式
7.如图所示,抛物线的函数表达式是( )
A.y=x2-x+4
B.y=-x2-x+4
C.y=x2+x+4
D.y=-x2+x+4
8.已知一个二次函数的图象与x轴的两个交点的坐标分别为(-1,0)和(2,0),与y轴的交点坐标为(0,-2),则该二次函数的解析式为_______________.
9.已知二次函数经过点A(2,4),B(-1,0),且在x轴上截得的线段长为2,求该函数的解析式.
中档题
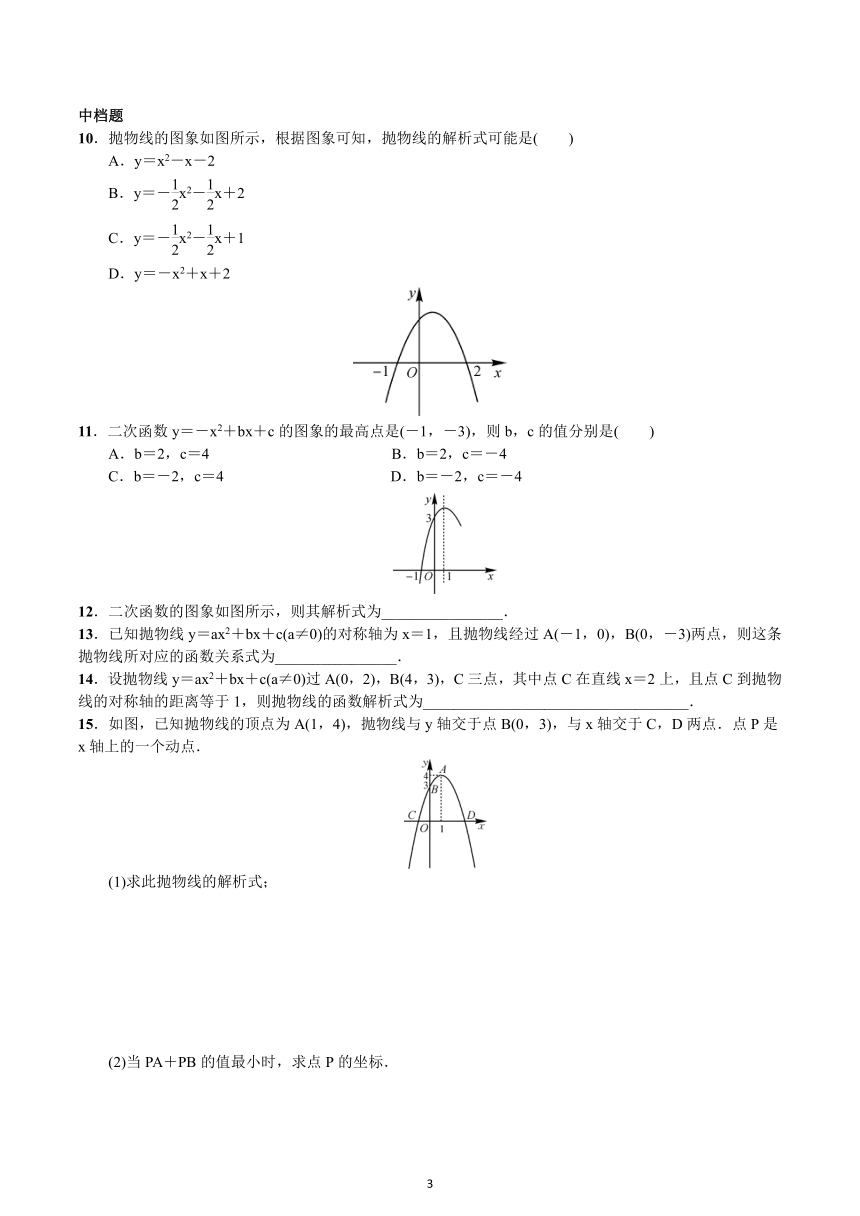
10.抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是( )
A.y=x2-x-2
B.y=-x2-x+2
C.y=-x2-x+1
D.y=-x2+x+2
11.二次函数y=-x2+bx+c的图象的最高点是(-1,-3),则b,c的值分别是( )
A.b=2,c=4 B.b=2,c=-4
C.b=-2,c=4 D.b=-2,c=-4
12.二次函数的图象如图所示,则其解析式为________________.
13.已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0),B(0,-3)两点,则这条抛物线所对应的函数关系式为________________.
14.设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数解析式为___________________________________.
15.如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标.
16.已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.
综合题
17.设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时函数的图象;
(2)根据图象,写出你发现的一条结论;
(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到函数y3的图象,求函数y3的最小值.
参考答案
基础题
1.y=-x2+4x-6 2.y=-2x2-12x-13
3.由题意,得解得∴二次函数的解析式为y=2x2-3x+1.
4.(1)∵抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,∴解得∴二次函数解析式是y=x2-2x-3.(2)∵y=x2-2x-3=(x-1)2-4,∴抛物线的对称轴为x=1,顶点坐标为(1,-4).
5.D
6.依题意,设y=a(x-h)2+k.将顶点坐标(4,-1)和与y轴交点(0,3)代入,得3=a(0-4)2-1.解得a=.∴这条抛物线的解析式为y=(x-4)2-1.
7.D 8.y=x2-x-2
9.∵B(-1,0)且在x轴上截得的线段长为2,∴与x轴的另一个交点坐标为(1,0)或(-3,0).设该函数解析式为y=a(x-x1)(x-x2),把A(2,4),B(-1,0),(1,0)代入得a(2+1)(2-1)=4,解得a=.所以y=(x+1)(x-1).同理,把A(2,4),B(-1,0),(-3,0)代入,可以求得y=(x+1)(x+3).∴函数的解析式为y=(x+1)(x-1)或y=(x+1)(x+3).
中档题
10.D 11.D 12.y=-x2+2x+3 13.y=x2-2x-3 14.y=x2-x+2或y=-x2+x+2
15.(1)∵抛物线顶点坐标为(1,4),∴设y=a(x-1)2+4.∵抛物线过点B(0,3),∴3=a(0-1)2+4,解得a=-1.∴抛物线的解析式为y=-(x-1)2+4,即y=-x2+2x+3.(2)作点B关于x轴的对称点E(0,-3),连接AE交x轴于点P.设AE解析式为y=kx+b,则解得∴yAE=7x-3.∵当y=0时,x=,∴点P的坐标为(,0).
16.(1)∵A(1,0),B(3,0),∴设抛物线解析式为y=a(x-1)(x-3).∵抛物线过(0,-3),∴-3=a(-1)×(-3).解得a=-1.∴y=-(x-1)(x-3)=-x2+4x-3.∵y=-x2+4x-3=-(x-2)2+1,∴顶点坐标为(2,1).(2)答案不唯一,如:先向左平移2个单位,再向下平移1个单位,得到的抛物线的解析式为y=-x2,平移后抛物线的顶点为(0,0)落在直线y=-x上.
综合题
(1)当k=0时,y=-(x-1)(x+3),所画函数图象图略.
①三个图象都过点(1,0)和点(-1,4);②图象总交x轴于点(1,0);③k取0和2时的函数图象关于点(0,2)中心对称;④函数y=(x-1)[(k-1)x+(x-3)]的图象都经过点(1,0)和点(-1,4);等等.(其他正确结论也行)
(3)将函数y2=(x-1)2的图象向左平移4个单位,再向下平移2个单位,得到函数y3=(x+3)2-2,∴当x=-3时,函数y3取最小值,等于-2.
基础题
知识点1 利用“三点式”求二次函数解析式
1.已知二次函数y=-x2+bx+c的图象经过A(2,0),B(0,-6)两点,则这个二次函数的解析式为______________________.
2.若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
x
-7
-6
-5
-4
-3
-2
y
-27
-13
-3
3
5
3
则此二次函数的解析式为____________________.
3.已知二次函数y=ax2+bx+c,当x=0时,y=1;当x=-1时,y=6;当x=1时,y=0.求这个二次函数的解析式.
4.如图,抛物线y=x2+bx+c与x轴交于A,B两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标.
知识点2 利用“顶点式”求二次函数解析式
5.已知某二次函数的图象如图所示,则这个二次函数的解析式为( )
A.y=2(x+1)2+8
B.y=18(x+1)2-8
C.y=(x-1)2+8
D.y=2(x-1)2-8
6.已知抛物线的顶点坐标为(4,-1),与y轴交于点(0,3),求这条抛物线的解析式.
知识点3 利用“交点式”求二次函数解析式
7.如图所示,抛物线的函数表达式是( )
A.y=x2-x+4
B.y=-x2-x+4
C.y=x2+x+4
D.y=-x2+x+4
8.已知一个二次函数的图象与x轴的两个交点的坐标分别为(-1,0)和(2,0),与y轴的交点坐标为(0,-2),则该二次函数的解析式为_______________.
9.已知二次函数经过点A(2,4),B(-1,0),且在x轴上截得的线段长为2,求该函数的解析式.
中档题
10.抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是( )
A.y=x2-x-2
B.y=-x2-x+2
C.y=-x2-x+1
D.y=-x2+x+2
11.二次函数y=-x2+bx+c的图象的最高点是(-1,-3),则b,c的值分别是( )
A.b=2,c=4 B.b=2,c=-4
C.b=-2,c=4 D.b=-2,c=-4
12.二次函数的图象如图所示,则其解析式为________________.
13.已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0),B(0,-3)两点,则这条抛物线所对应的函数关系式为________________.
14.设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数解析式为___________________________________.
15.如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标.
16.已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.
综合题
17.设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时函数的图象;
(2)根据图象,写出你发现的一条结论;
(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到函数y3的图象,求函数y3的最小值.
参考答案
基础题
1.y=-x2+4x-6 2.y=-2x2-12x-13
3.由题意,得解得∴二次函数的解析式为y=2x2-3x+1.
4.(1)∵抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,∴解得∴二次函数解析式是y=x2-2x-3.(2)∵y=x2-2x-3=(x-1)2-4,∴抛物线的对称轴为x=1,顶点坐标为(1,-4).
5.D
6.依题意,设y=a(x-h)2+k.将顶点坐标(4,-1)和与y轴交点(0,3)代入,得3=a(0-4)2-1.解得a=.∴这条抛物线的解析式为y=(x-4)2-1.
7.D 8.y=x2-x-2
9.∵B(-1,0)且在x轴上截得的线段长为2,∴与x轴的另一个交点坐标为(1,0)或(-3,0).设该函数解析式为y=a(x-x1)(x-x2),把A(2,4),B(-1,0),(1,0)代入得a(2+1)(2-1)=4,解得a=.所以y=(x+1)(x-1).同理,把A(2,4),B(-1,0),(-3,0)代入,可以求得y=(x+1)(x+3).∴函数的解析式为y=(x+1)(x-1)或y=(x+1)(x+3).
中档题
10.D 11.D 12.y=-x2+2x+3 13.y=x2-2x-3 14.y=x2-x+2或y=-x2+x+2
15.(1)∵抛物线顶点坐标为(1,4),∴设y=a(x-1)2+4.∵抛物线过点B(0,3),∴3=a(0-1)2+4,解得a=-1.∴抛物线的解析式为y=-(x-1)2+4,即y=-x2+2x+3.(2)作点B关于x轴的对称点E(0,-3),连接AE交x轴于点P.设AE解析式为y=kx+b,则解得∴yAE=7x-3.∵当y=0时,x=,∴点P的坐标为(,0).
16.(1)∵A(1,0),B(3,0),∴设抛物线解析式为y=a(x-1)(x-3).∵抛物线过(0,-3),∴-3=a(-1)×(-3).解得a=-1.∴y=-(x-1)(x-3)=-x2+4x-3.∵y=-x2+4x-3=-(x-2)2+1,∴顶点坐标为(2,1).(2)答案不唯一,如:先向左平移2个单位,再向下平移1个单位,得到的抛物线的解析式为y=-x2,平移后抛物线的顶点为(0,0)落在直线y=-x上.
综合题
(1)当k=0时,y=-(x-1)(x+3),所画函数图象图略.
①三个图象都过点(1,0)和点(-1,4);②图象总交x轴于点(1,0);③k取0和2时的函数图象关于点(0,2)中心对称;④函数y=(x-1)[(k-1)x+(x-3)]的图象都经过点(1,0)和点(-1,4);等等.(其他正确结论也行)
(3)将函数y2=(x-1)2的图象向左平移4个单位,再向下平移2个单位,得到函数y3=(x+3)2-2,∴当x=-3时,函数y3取最小值,等于-2.
同课章节目录
