第三章位置与坐标整章教案(表格形式)
文档属性
| 名称 | 第三章位置与坐标整章教案(表格形式) |  | |
| 格式 | zip | ||
| 文件大小 | 330.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-28 10:39:33 | ||
图片预览




文档简介
课 时 教 案
第 周 星期 第 节 年 月 日
课 题 1. 确定位置
教 学 目 标 (1)理解用一对数表示物体在平面内所在的位置,灵活运用不同的方式确定物体的位置; (2)经历在现实生活中确定物体位置的过程,感受确定物体位置的多种方法; (3)体验生活中处处有确定位置,感受现实生活中确定位置的必要性.
教 材 分析 重 点 理解在平面内确定一个物体的位置一般需要两个数据;
难 点 灵活地运用不同的方式确定物体的位置。
教 具 电脑、投影仪 二次备课
教 学 过 程 第一环节 感受生活中的情境,导入新课通过若干图片,引导学生感受生活中常常需要确定位置.导入新课:怎样确定位置呢?——§3.1确定位置。第二环节 分类讨论,探索新知 1.温故启新(1)温故:在数轴上,确定一个点的位置需要几个数据呢? 答:一个,例如,若A点表示-2,B点表示3,则由-2和3就可以在数轴上找到A点和B点的位置。总结得出结论:在直线上, 确定一个点的位置一般需要一个数据.(2)启新:在平面内,又如何确定一个点的位置呢?请同学们根据生活中确定位置的实例,请谈谈自己的看法.2.举例探究 Ⅰ. 探究1 (1)在电影院内如何找到电影票上指定的位置?(2)在电影票上“6排3号”与“3排6号”中的“6”的含义有什么不同?(3)如果将“6排3号”简记作(6,3),那么“3排6号”如何表示?(5,6)表示什么含义? (4) 在只有一层的电影院内,确定一个座位一般需要几个数据?结论:生活中常常用“排数”和“号数”来确定位置.
教 学 过 程 Ⅱ. 学有所用(1) 你能用两个数据表示你现在所坐的位置吗?结论:生活中常常用“行数”和“列数”来确定位置. Ⅲ. 探究2. 据新华社报道,1976年7月28日 凌晨3时40分,我国河北省唐山市发生里氏7.8级的大地震,震中位于唐山市吉祥路一带,即北纬39°38′,东经118°11′.这次地震中,有24万人丧生,是有史以来地震给人类造成的特大灾难之一.你能在地图上找出震中的大致位置吗?结论:生活中常常用“经度”和“纬度”来确定位置. Ⅳ. 探究3 下图是某次海战中敌我双方舰艇对峙示意图(图中1厘米表示20海里).对我方舰艇来说:(1)北偏东40°的方向上有哪些目标?要想确定敌舰B的位置,还需要什么数据?(2)距我方潜艇20海里处的敌舰有哪几艘?(3)要确定每艘敌舰的位置,各需要几个数据?(4) 如何表示敌舰A,B,C的位置?结论:生活中常常用“方位角”和“距离”来确定位置. Ⅵ.探究4 如图是西安市地图的一部分,如何向同伴介绍“省政府”所在的区域?“省图书馆”?结论:生活中常常用“区域定位”来确定位置.第三环节 学有所用.1.在平面内,下列数据不能确定物体位置的是( ) A.3楼5号 B.北偏西40° C.解放路30号 D.东经120°,北纬30°第四环节 感悟与收获1.知识能力: (1)在现实情境中感受了确定物体位置的多种方式,并能灵活运用不同方式确定物体的位置. (2)在直线上,确定一个点的位置一般需要一个数据;在平面内,确定一个点的位置一般需要两个数据; 在空间内,确定一个点的位置一般需要三个数据.2.思想方法: (1)数形结合;(2)分类讨论;(3)感受生活—认知规律—运用规律.
作业 C 类:教材习题3.1第1,2,3题; B 类:用适当的方法向你的同学介绍你所熟悉的一处西安旅游景点的位置;A 类:写一篇关于生活中如何确定位置的小文章.
后记
课 时 教 案
第 周 星期 第 节 年 月 日
课 题 2 平面直角坐标系(第1课时)
教 学 目 标 1.理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念; 2.认识并能画出平面直角坐标系; 3.能在给定的直角坐标系中,由点的位置写出它的坐标。 1.通过画坐标系、由点找坐标等过程,发展学生的数形结合意识、合作交流意识; 2.通过对一些点的坐标进行观察,探索坐标轴上点的坐标有什么特点,纵坐标或横坐标相同的点所连成的线段与两坐标轴之间的关系。
教 材 分析 重 点 1.理解平面直角坐标系的有关知识; 2.在给定的平面直角坐标系中,会根据点的位置写出它的坐标;
难 点 1.横(或纵)坐标相同的点的连线与坐标轴的关系的探究; 2.坐标轴上点的坐标有什么特点的总结。
教 具 电脑、投影仪 二次备课
教 学 过 程 第一环节 感受生活中的情境,导入新课同学们,你们喜欢旅游吗? 假如你到了某一个城市旅游,那么你应怎样确定旅游景点的位置呢?下面给出一张某市旅游景点的示意图,根据示意图(图5-6),回答以下问题: 你是怎样确定各个景点位置的? “大成殿”在“中心广场”南、西各多少个格?“碑林”在“中心广场”北、东各多少个格? 如果以“中心广场”为原点作两条互相垂直的数轴,分别取向右、向上的方向为数轴的正方向,一个方格的边长看做一个单位长度,那么你能表示“碑林”的位置吗?“大成殿”的位置呢? 在上一节课,我们已经学习了许多确定位置的方法,这个问题中,大家看用哪种方法比较合适?第二环节 分类讨论,探索新知1.平面直角坐标系、横轴、纵轴、横坐标、纵坐标、原点的定义和象限的划分。 学生自学课本,理解上述概念。
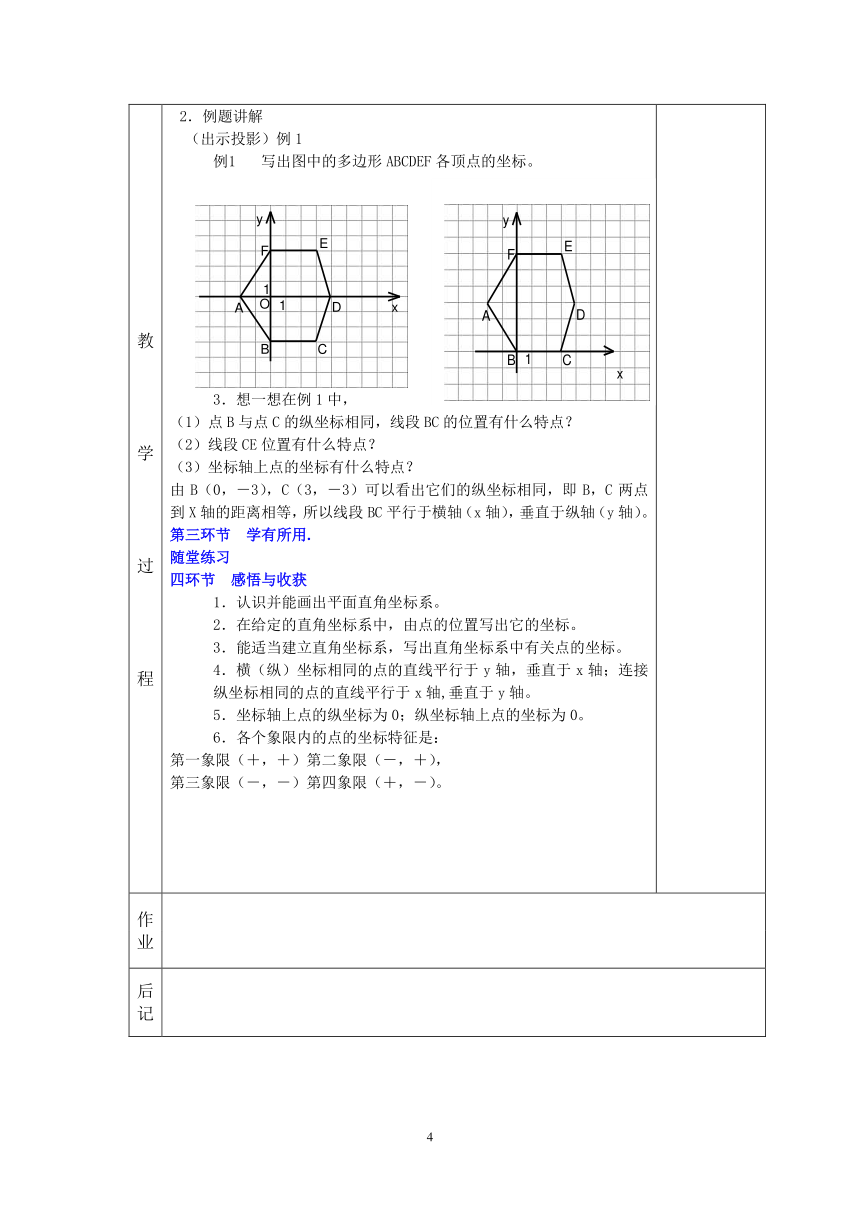
教 学 过 程 2.例题讲解 (出示投影)例1 写出图中的多边形ABCDEF各顶点的坐标。想一想在例1中, (1)点B与点C的纵坐标相同,线段BC的位置有什么特点? (2)线段CE位置有什么特点? (3)坐标轴上点的坐标有什么特点? 由B(0,-3),C(3,-3)可以看出它们的纵坐标相同,即B,C两点到X轴的距离相等,所以线段BC平行于横轴(x轴),垂直于纵轴(y轴)。第三环节 学有所用.随堂练习四环节 感悟与收获1.认识并能画出平面直角坐标系。 2.在给定的直角坐标系中,由点的位置写出它的坐标。 3.能适当建立直角坐标系,写出直角坐标系中有关点的坐标。 4.横(纵)坐标相同的点的直线平行于y轴,垂直于x轴;连接纵坐标相同的点的直线平行于x轴,垂直于y轴。 5.坐标轴上点的纵坐标为0;纵坐标轴上点的坐标为0。 6.各个象限内的点的坐标特征是:
第一象限(+,+)第二象限(-,+),
第三象限(-,-)第四象限(+,-)。
作业
后记
课 时 教 案
第 周 星期 第 节 年 月 日
课 题 2.平面直角坐标系(第2课时)
教 学 目 标 1.知道在坐标轴上的点以及与坐标轴平行的直线上点的坐标的特征. 2.知道不同象限点的坐标的特征。 3.经历画坐标系、描点、连线、看图以及由点找坐标等过程,进一步体会平面直角坐标系中点与坐标之间的对应关系,发展数形结合意识。
教 材 分析 重 点 体会平面直角坐标系中点与坐标之间的对应关系,发展数形结合意识。
难 点 体会平面直角坐标系中点与坐标之间的对应关系,发展数形结合意识。
教 具 电脑、投影仪 二次备课
教 学 过 程 第一环节 感受生活中的情境,导入新课.在上节课中我们学习了平面直角坐标系的定义,以及横轴、纵轴、点的坐标的定义,练习了在平面直角坐标系中由点找坐标,还探讨了横坐标或纵坐标相同的点的连线与坐标轴的关系,坐标轴上点的坐标有什么特点。1、探究坐标轴上点或与坐标轴平行的直线上点的坐标的特征.在直角坐标系中描出下列各点,并将各组内这些点依次用线段连接起来.(1)D(-3,5),E(-7,3),F(-6,3),B(0,3),C(1,3),D(-3,5); (2)F(-6,3),G(-6,0),A(0,0),B(0,3); 观察所描出的图形,它像什么? 解答下列问题 (1)点G与点A的坐标有什么共同特点?在坐标系中它们的位置又有什么共同特点? (2)线段EC与x轴有什么特殊的位置关系?点E、点C的坐标有什么特点?线段EC上其它点的坐标呢? (3)点F、点G的坐标有什么共同特点,线段FG与Y轴有怎样的位置关系?解答:(1)线段 AG 上的点都在 x 轴上,它们的纵坐标等于 0; 线段 AB 上的点都在 y 轴上,它们的横坐标等于 0. (2)线段 EC 平行于 x 轴,点 E 和点 C 的纵坐标相同. 线段 EC 上其他点的纵坐标相同,都是 3.(3)点 F 和点G 的横坐标相同,线段 FG 与 y 轴平行.
教 学 过 程 由点找坐标是已知点在直角坐标系中的位置,根据这点在方格纸上对应的x轴、y轴上的数字写出它的坐标,反过来,已知坐标,让你在直角坐标系中找点,你能找到吗?这就是本节课的内容。第二环节 分类讨论,探索新知.1.请同学们拿出准备好的方格纸,自己建立平面直角坐标系,然后按照我给出的坐标,在直角坐标系中描点,并依次用线段连接起来。 (-9,3),(-9,0),(-3,0),(-3,3) (学生操作) 2.(出示投影)还是在这个平面直角坐标系中,描出下列各组内的点用线段依次连接起来。 (1)(-6,5),(-10,3),(-9,3),(-3,3),(-2,3),(-6,5); (2)(3.5,9),(2,7),(3,7),(4,7),(5,7),(3.5,9); (3)(3,7),(1,5),(2,5),(5,5),(6,5),(4,7); (4)(2,5),(0,3),(3,3),(3,0),(4,0),(4,3),(7,3),(5,5)。 观察所得的图形,你觉得它像什么?。 3.做一做 (出示投影) 在书上已建立的直角坐标系画,要求每位同学独立完成。第三环节 学有所用.1.在直角坐标系中描出下列各点,并将各组内的点用线段顺次连接起来。 (1)(0,3),(-4,0),(0,-3),(4,0),(0,3); (2)(0,0),(4,-3),(8,0),(4,3),(0,0); (3)(2,0)2. 如图所示的笑脸中, (1)在“笑脸”上找出几个位于第一象限的点,指出它们的坐标,说说这些点的坐标有什么特点。 (2)在其他象限内分别找几个点,看看其他各个象限内的点的坐标有什么特点。2.不具体标出这些点,分别判断(1,2),(-1,-3),(2.,-1),(-3,4)这些点所在的象限,说说你是怎么判断的。第四环节 感悟与收获1.位于x轴上的点的坐标的特征是: ; 位于y轴上的点的坐标的特征是: 。 2.与x轴平行的直线上点的坐标的特征是: ; 与y轴平行的直线上点的坐标的特征是: 。
作业
后记
课 时 教 案
第 周 星期 第 节 年 月 日
课 题 2.平面直角坐标系(第三课时)
教 学 目 标 1、能结合所给图形的特点,建立适当的坐标系,写出点的坐标; 2、能根据一些特殊点的坐标复原坐标系; 3、经历建立坐标系描述图形的过程,进一步发展数形结合意识。
教 材 分析 重 点 根据实际问题建立适当的坐标系,并能写出各点的坐标。
难 点 根据一些特殊点的坐标复原坐标系;
教 具 电脑、投影仪 二次备课
教 学 过 程 第一环节:探究建立平面直角坐标系,描述图形1.如图,矩形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标。『师』:在没有直角坐标系的情况下不能写出各个顶点的坐标,所以应先建立直角坐标系,那么应如何选取直角坐标系呢?请大家思考。 『生1』:如下图所示,以点C为坐标原点,分别以CD,CB所在直线为x轴、y轴,建立直角坐标系。 由CD的长为6,CB长为4,可得A,B,C,D的坐标分别为A(6,4),B(0,4),C(0,0),D(6,0)。 『生2』 :如下图所示,以点D为坐标原点,分别以CD,AD所在直线为x轴、y轴,建立直角坐标系。 『生3』:有,如下图所示,以矩形的中心(即对角线的交点)为坐标原点,平行于矩形相邻两边的直线为x轴、y轴建立直角坐标系,则A,B,C,D的坐标分别为A(3,2),B(-3,2),C(-3,-2),D(3,-2)。
教 学 过 程 第二环节:应用对于边长为4的整三角形ABC,建立适当的直角坐标系,写出各个顶点的坐标。 解:略(见书)。 议一议 你认为怎样建立适合的直角坐标系?第三环节:巩固如图,建立两个不同的直角坐标系,在各个直角坐标系中,分别写出八角星8个角的顶点的坐标,并比较同一顶点在两个坐标系中的坐标. 2.如图,在一次军棋比赛中,如果团长所在的位置的坐标为(2,-5),司令所在的位置的坐标为(4,-2),那么工兵所在的位置的坐标为 。这里仅仅提出问题,激发兴趣,并不要求现在解决,而希望在本节课后面再回解该问题。第四环节:练习随堂练习 (体现建立直角坐标系的多样性)第五环节:小结内容:小结本节课自己的收获和进步,从知识和能力上两个方面总结,老师予于肯定和鼓励。 目的:鼓励学生大胆发言,敢于表达自己的观点,同时学生之间可以相互学习,共同提高,老师给予肯定和鼓励,激发学生的学习热情。
作业 课本习题5.5
后记
课 时 教 案
第 周 星期 第 节 年 月 日
课 题 3. 轴对称与坐标变化
教 学 目 标 1、在同一直角坐标系中,感受图形上点的坐标变化与图形的轴对称变换之间的关系. 2、经历图形坐标变化与图形轴对称之间关系的探索过程,发展形象思维能力和数形结合意识。3.经历探究物体与图形的形状、大小、位置关系和变换的过程,掌握空间与图形的基础知识和基本技能,培养学生的探索能力。
教 材 分析 重 点 经历图形坐标变化与图形轴对称之间关系的探索过程,明确图形坐标变化与图形轴对称之间关系。
难 点 由坐标的变化探索新旧图形之间的变化探索过程,发展形象思维能力和数形结合意识。
教 具 电脑、投影仪 二次备课
教 学 过 程 第一环节 创设问题情境,引入新课『师』:在前几节课中我们学习了平面直角坐标系的有关知识,会画平面直角坐标系;能在方格纸上建立适当的直角坐标系,描述物体的位置;在给定的直角坐标系下,会根据坐标描出点的位置,由点的位置写出它的坐标。 我们知道点的位置不同写出的坐标就不同,反过来,不同的坐标确定不同的点。如果坐标中的横(纵)坐标不变,纵(横)坐标按一定的规律变化,或者横纵坐标都按一定的规律变化,那么图形是否会变化,变化的规律是怎样的,这将是本节课中我们要研究的问题。 探索两个关于坐标轴对称的图形的坐标关系1.在如图所示的平面直角坐标系中,第一、二象限内各有一面小旗。 两面小旗之间有怎样的位置关系?对应点A与A1的坐标又有什么特点?其它对应的点也有这个特点吗? 2.在右边的坐标系内,任取一点,做出这个点关于y轴对称的点,看看两个点的坐标有什么样的位置关系,说说其中的道理。 3.如果关于x轴对称呢? 在这个坐标系里作出小旗ABCD关于x轴的对称图形,它的各个顶点的坐标与原来的点的坐标有什么关系?
教 学 过 程 4.关于x轴对称的两点,它们的横坐标 ,纵坐标 ; 关于y轴对称的两点,它们的横坐标 ,纵坐标 。 5.已知点P(2a-3,3),点A(-1,3b+2), (1)如果点P与点A关于x轴对称,那么a+b= ; (2)如果点P与点A关于y轴对称,那么a+b= 。 拿出方格纸,并在方格纸上建立直角坐标系,根据我读出的点的坐标在纸上找到相应的点,并依次用线段将这些点连接起来。坐标是(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)。 观察所得的图形,你们觉得它像什么? 下面我们把坐标适当地作些变化,这条鱼就能变大或变胖,即变化的鱼。第二环节 探究新知:例1 将上图中的点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)做以下变化: (1)纵坐标保持不变,横坐标分别乘以-1,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化? (2)横坐标保持不变,纵坐标分别乘以-1,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化? (3)横坐标、纵坐标都分别乘以-1,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?第三环节 拓展练习:1.点 A(2,- 3)关 于 x 轴 对 称 的 点 的 坐 标 是( ).
2.点 B( - 2,1)关 于 y 轴 对 称 的 点 的 坐 标 是( ). 3.点(4,3)与点(4,- 3)的关系是( ) . A.关于原点对称 B.关于 x轴对称
C.关于 y轴对称 D.不能构成对称关系
4.点(m,- 1)和点(2,n)关于 x轴对称,则 mn等于( ) A.- 2 B.2 C.1 D.- 1 5.(1)若 mn = 0,则点 P(m,n)必定在 上.
(2)已知点 P( a,b),Q(3,6),且 PQ ∥ x轴,则b的值为 . 第四环节 课堂小结1、关于y轴对称的两个图形上点的坐标特征:(x , y)——(- x , y)2、关于x轴对称的两个图形上点的坐标特征:(x , y)——(x , - y)3、关于原点对称的两个图形上点的坐标特征:(x , y)——(- x , -y)
作业 习题3.5 1,2,3
后记 教学中务必给学生创造自主学习与合作交流的机会,留给学生充足的动手机会和思考空间,教师不要急于下结论。事先一定要准备好坐标纸等,提高课堂效率。
课 时 教 案
第 周 星期 第 节 年 月 日
课 题 《位置与坐标》回顾与思考
教 学 目 标 从现实生活中体会确定位置的不同方式与方法,感受确定位置的多样性; 掌握利用直角坐标系确定位置的方法; 会用平面直角坐标系来解决一些简单的实际问题;
教 材 分析 重 点 掌握利用直角坐标系确定位置的方法;
难 点 会用平面直角坐标系来解决一些简单的
教 具 电脑、投影仪 二次备课
教 学 过 程 学习过程 活动1 知识梳理1、在平面内,确定点的位置一般需要几个数据?举例说明。 2、平面直角坐标系中,如何确定给定点的坐标?给定坐标,如何确定对应的点?分别举例说明。 3、平面直角坐标系中,坐标轴上的点具有什么特点?平行于坐标轴的线段上的点,它们的坐标之间有什么样的关系?分别举例说明。 4.平面直角坐标系中,关于坐标轴对称的点的坐标之间具有怎样的关系?反过来坐标具有这样的关系的点关于坐标轴对称吗?这些结论可以帮助你解决哪些问题? 5、通过上述知识的回顾,请你整理出本章的知识框架图:活动2:典型例析例1.右图是某市几个旅游景点的示意图(图中每个小正方形的边长为1个单位长度)。 请以某景点为原点,画出直角坐标系,并用坐标表示出下列景点的位置:光岳楼___________、 湖心岛___________、金凤广场__________、动物园___________。
教 学 过 程 反思。交流与同伴比较,你们得到的各个景点的坐标一样吗?判断各自的做法是否正确,说说出现差异的原因。例2.已知平面直角坐标系上有六个点: 请将上述六个点按下列要求分成两类,并写出同类点具有而另一类点不具有的一个特征(请将答案按要求写在横线上,点用字母表示). ⑴甲类含两个点,乙类含其余四个点. 甲类:点____,____是同一类点,其特征是__ ___; 乙类:点____,____,____,____是同一类点,其特征是__ ____; ⑵甲类含三个点,乙类含其余三个点. 甲类:点___,___,____是同一类点,其特征是__ _____; 乙类:点___,___,____是同一类点,其特征是___ ____.反思交流你们的结果一样吗?关于分类,你们有哪些经验?与同伴交流。例3.如图,已知A、B两村庄的坐标分别为(2,2)、(7,4),一辆汽车在轴上行驶,从原点O出发。 (1)汽车行驶到什么位置时离A村最近?写出此点的坐标。(2)汽车行驶到什么位置时离B村最近?写出此点的坐标。*(3)汽车行驶到什么位置时,距离两村的和最短?请在图中画出这个位置,并求出此时汽车到两村距离的和。活动3:自主反馈1(1)如图,正八边形的边长为2,点C的坐标是(,0)写出其余各点的坐标:(2)如果在(1)中做出正八边形关于x轴对称的图形,则可以得到一个“8”字形,试尽快写出这个“8”字形另外六个顶点的坐标。 (3)试换一个点为原点,建立另一个坐标系,并写出各个顶点的坐标。
作业
后记
A
B
C
D
O
H
G
E
F
x
第 周 星期 第 节 年 月 日
课 题 1. 确定位置
教 学 目 标 (1)理解用一对数表示物体在平面内所在的位置,灵活运用不同的方式确定物体的位置; (2)经历在现实生活中确定物体位置的过程,感受确定物体位置的多种方法; (3)体验生活中处处有确定位置,感受现实生活中确定位置的必要性.
教 材 分析 重 点 理解在平面内确定一个物体的位置一般需要两个数据;
难 点 灵活地运用不同的方式确定物体的位置。
教 具 电脑、投影仪 二次备课
教 学 过 程 第一环节 感受生活中的情境,导入新课通过若干图片,引导学生感受生活中常常需要确定位置.导入新课:怎样确定位置呢?——§3.1确定位置。第二环节 分类讨论,探索新知 1.温故启新(1)温故:在数轴上,确定一个点的位置需要几个数据呢? 答:一个,例如,若A点表示-2,B点表示3,则由-2和3就可以在数轴上找到A点和B点的位置。总结得出结论:在直线上, 确定一个点的位置一般需要一个数据.(2)启新:在平面内,又如何确定一个点的位置呢?请同学们根据生活中确定位置的实例,请谈谈自己的看法.2.举例探究 Ⅰ. 探究1 (1)在电影院内如何找到电影票上指定的位置?(2)在电影票上“6排3号”与“3排6号”中的“6”的含义有什么不同?(3)如果将“6排3号”简记作(6,3),那么“3排6号”如何表示?(5,6)表示什么含义? (4) 在只有一层的电影院内,确定一个座位一般需要几个数据?结论:生活中常常用“排数”和“号数”来确定位置.
教 学 过 程 Ⅱ. 学有所用(1) 你能用两个数据表示你现在所坐的位置吗?结论:生活中常常用“行数”和“列数”来确定位置. Ⅲ. 探究2. 据新华社报道,1976年7月28日 凌晨3时40分,我国河北省唐山市发生里氏7.8级的大地震,震中位于唐山市吉祥路一带,即北纬39°38′,东经118°11′.这次地震中,有24万人丧生,是有史以来地震给人类造成的特大灾难之一.你能在地图上找出震中的大致位置吗?结论:生活中常常用“经度”和“纬度”来确定位置. Ⅳ. 探究3 下图是某次海战中敌我双方舰艇对峙示意图(图中1厘米表示20海里).对我方舰艇来说:(1)北偏东40°的方向上有哪些目标?要想确定敌舰B的位置,还需要什么数据?(2)距我方潜艇20海里处的敌舰有哪几艘?(3)要确定每艘敌舰的位置,各需要几个数据?(4) 如何表示敌舰A,B,C的位置?结论:生活中常常用“方位角”和“距离”来确定位置. Ⅵ.探究4 如图是西安市地图的一部分,如何向同伴介绍“省政府”所在的区域?“省图书馆”?结论:生活中常常用“区域定位”来确定位置.第三环节 学有所用.1.在平面内,下列数据不能确定物体位置的是( ) A.3楼5号 B.北偏西40° C.解放路30号 D.东经120°,北纬30°第四环节 感悟与收获1.知识能力: (1)在现实情境中感受了确定物体位置的多种方式,并能灵活运用不同方式确定物体的位置. (2)在直线上,确定一个点的位置一般需要一个数据;在平面内,确定一个点的位置一般需要两个数据; 在空间内,确定一个点的位置一般需要三个数据.2.思想方法: (1)数形结合;(2)分类讨论;(3)感受生活—认知规律—运用规律.
作业 C 类:教材习题3.1第1,2,3题; B 类:用适当的方法向你的同学介绍你所熟悉的一处西安旅游景点的位置;A 类:写一篇关于生活中如何确定位置的小文章.
后记
课 时 教 案
第 周 星期 第 节 年 月 日
课 题 2 平面直角坐标系(第1课时)
教 学 目 标 1.理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念; 2.认识并能画出平面直角坐标系; 3.能在给定的直角坐标系中,由点的位置写出它的坐标。 1.通过画坐标系、由点找坐标等过程,发展学生的数形结合意识、合作交流意识; 2.通过对一些点的坐标进行观察,探索坐标轴上点的坐标有什么特点,纵坐标或横坐标相同的点所连成的线段与两坐标轴之间的关系。
教 材 分析 重 点 1.理解平面直角坐标系的有关知识; 2.在给定的平面直角坐标系中,会根据点的位置写出它的坐标;
难 点 1.横(或纵)坐标相同的点的连线与坐标轴的关系的探究; 2.坐标轴上点的坐标有什么特点的总结。
教 具 电脑、投影仪 二次备课
教 学 过 程 第一环节 感受生活中的情境,导入新课同学们,你们喜欢旅游吗? 假如你到了某一个城市旅游,那么你应怎样确定旅游景点的位置呢?下面给出一张某市旅游景点的示意图,根据示意图(图5-6),回答以下问题: 你是怎样确定各个景点位置的? “大成殿”在“中心广场”南、西各多少个格?“碑林”在“中心广场”北、东各多少个格? 如果以“中心广场”为原点作两条互相垂直的数轴,分别取向右、向上的方向为数轴的正方向,一个方格的边长看做一个单位长度,那么你能表示“碑林”的位置吗?“大成殿”的位置呢? 在上一节课,我们已经学习了许多确定位置的方法,这个问题中,大家看用哪种方法比较合适?第二环节 分类讨论,探索新知1.平面直角坐标系、横轴、纵轴、横坐标、纵坐标、原点的定义和象限的划分。 学生自学课本,理解上述概念。
教 学 过 程 2.例题讲解 (出示投影)例1 写出图中的多边形ABCDEF各顶点的坐标。想一想在例1中, (1)点B与点C的纵坐标相同,线段BC的位置有什么特点? (2)线段CE位置有什么特点? (3)坐标轴上点的坐标有什么特点? 由B(0,-3),C(3,-3)可以看出它们的纵坐标相同,即B,C两点到X轴的距离相等,所以线段BC平行于横轴(x轴),垂直于纵轴(y轴)。第三环节 学有所用.随堂练习四环节 感悟与收获1.认识并能画出平面直角坐标系。 2.在给定的直角坐标系中,由点的位置写出它的坐标。 3.能适当建立直角坐标系,写出直角坐标系中有关点的坐标。 4.横(纵)坐标相同的点的直线平行于y轴,垂直于x轴;连接纵坐标相同的点的直线平行于x轴,垂直于y轴。 5.坐标轴上点的纵坐标为0;纵坐标轴上点的坐标为0。 6.各个象限内的点的坐标特征是:
第一象限(+,+)第二象限(-,+),
第三象限(-,-)第四象限(+,-)。
作业
后记
课 时 教 案
第 周 星期 第 节 年 月 日
课 题 2.平面直角坐标系(第2课时)
教 学 目 标 1.知道在坐标轴上的点以及与坐标轴平行的直线上点的坐标的特征. 2.知道不同象限点的坐标的特征。 3.经历画坐标系、描点、连线、看图以及由点找坐标等过程,进一步体会平面直角坐标系中点与坐标之间的对应关系,发展数形结合意识。
教 材 分析 重 点 体会平面直角坐标系中点与坐标之间的对应关系,发展数形结合意识。
难 点 体会平面直角坐标系中点与坐标之间的对应关系,发展数形结合意识。
教 具 电脑、投影仪 二次备课
教 学 过 程 第一环节 感受生活中的情境,导入新课.在上节课中我们学习了平面直角坐标系的定义,以及横轴、纵轴、点的坐标的定义,练习了在平面直角坐标系中由点找坐标,还探讨了横坐标或纵坐标相同的点的连线与坐标轴的关系,坐标轴上点的坐标有什么特点。1、探究坐标轴上点或与坐标轴平行的直线上点的坐标的特征.在直角坐标系中描出下列各点,并将各组内这些点依次用线段连接起来.(1)D(-3,5),E(-7,3),F(-6,3),B(0,3),C(1,3),D(-3,5); (2)F(-6,3),G(-6,0),A(0,0),B(0,3); 观察所描出的图形,它像什么? 解答下列问题 (1)点G与点A的坐标有什么共同特点?在坐标系中它们的位置又有什么共同特点? (2)线段EC与x轴有什么特殊的位置关系?点E、点C的坐标有什么特点?线段EC上其它点的坐标呢? (3)点F、点G的坐标有什么共同特点,线段FG与Y轴有怎样的位置关系?解答:(1)线段 AG 上的点都在 x 轴上,它们的纵坐标等于 0; 线段 AB 上的点都在 y 轴上,它们的横坐标等于 0. (2)线段 EC 平行于 x 轴,点 E 和点 C 的纵坐标相同. 线段 EC 上其他点的纵坐标相同,都是 3.(3)点 F 和点G 的横坐标相同,线段 FG 与 y 轴平行.
教 学 过 程 由点找坐标是已知点在直角坐标系中的位置,根据这点在方格纸上对应的x轴、y轴上的数字写出它的坐标,反过来,已知坐标,让你在直角坐标系中找点,你能找到吗?这就是本节课的内容。第二环节 分类讨论,探索新知.1.请同学们拿出准备好的方格纸,自己建立平面直角坐标系,然后按照我给出的坐标,在直角坐标系中描点,并依次用线段连接起来。 (-9,3),(-9,0),(-3,0),(-3,3) (学生操作) 2.(出示投影)还是在这个平面直角坐标系中,描出下列各组内的点用线段依次连接起来。 (1)(-6,5),(-10,3),(-9,3),(-3,3),(-2,3),(-6,5); (2)(3.5,9),(2,7),(3,7),(4,7),(5,7),(3.5,9); (3)(3,7),(1,5),(2,5),(5,5),(6,5),(4,7); (4)(2,5),(0,3),(3,3),(3,0),(4,0),(4,3),(7,3),(5,5)。 观察所得的图形,你觉得它像什么?。 3.做一做 (出示投影) 在书上已建立的直角坐标系画,要求每位同学独立完成。第三环节 学有所用.1.在直角坐标系中描出下列各点,并将各组内的点用线段顺次连接起来。 (1)(0,3),(-4,0),(0,-3),(4,0),(0,3); (2)(0,0),(4,-3),(8,0),(4,3),(0,0); (3)(2,0)2. 如图所示的笑脸中, (1)在“笑脸”上找出几个位于第一象限的点,指出它们的坐标,说说这些点的坐标有什么特点。 (2)在其他象限内分别找几个点,看看其他各个象限内的点的坐标有什么特点。2.不具体标出这些点,分别判断(1,2),(-1,-3),(2.,-1),(-3,4)这些点所在的象限,说说你是怎么判断的。第四环节 感悟与收获1.位于x轴上的点的坐标的特征是: ; 位于y轴上的点的坐标的特征是: 。 2.与x轴平行的直线上点的坐标的特征是: ; 与y轴平行的直线上点的坐标的特征是: 。
作业
后记
课 时 教 案
第 周 星期 第 节 年 月 日
课 题 2.平面直角坐标系(第三课时)
教 学 目 标 1、能结合所给图形的特点,建立适当的坐标系,写出点的坐标; 2、能根据一些特殊点的坐标复原坐标系; 3、经历建立坐标系描述图形的过程,进一步发展数形结合意识。
教 材 分析 重 点 根据实际问题建立适当的坐标系,并能写出各点的坐标。
难 点 根据一些特殊点的坐标复原坐标系;
教 具 电脑、投影仪 二次备课
教 学 过 程 第一环节:探究建立平面直角坐标系,描述图形1.如图,矩形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标。『师』:在没有直角坐标系的情况下不能写出各个顶点的坐标,所以应先建立直角坐标系,那么应如何选取直角坐标系呢?请大家思考。 『生1』:如下图所示,以点C为坐标原点,分别以CD,CB所在直线为x轴、y轴,建立直角坐标系。 由CD的长为6,CB长为4,可得A,B,C,D的坐标分别为A(6,4),B(0,4),C(0,0),D(6,0)。 『生2』 :如下图所示,以点D为坐标原点,分别以CD,AD所在直线为x轴、y轴,建立直角坐标系。 『生3』:有,如下图所示,以矩形的中心(即对角线的交点)为坐标原点,平行于矩形相邻两边的直线为x轴、y轴建立直角坐标系,则A,B,C,D的坐标分别为A(3,2),B(-3,2),C(-3,-2),D(3,-2)。
教 学 过 程 第二环节:应用对于边长为4的整三角形ABC,建立适当的直角坐标系,写出各个顶点的坐标。 解:略(见书)。 议一议 你认为怎样建立适合的直角坐标系?第三环节:巩固如图,建立两个不同的直角坐标系,在各个直角坐标系中,分别写出八角星8个角的顶点的坐标,并比较同一顶点在两个坐标系中的坐标. 2.如图,在一次军棋比赛中,如果团长所在的位置的坐标为(2,-5),司令所在的位置的坐标为(4,-2),那么工兵所在的位置的坐标为 。这里仅仅提出问题,激发兴趣,并不要求现在解决,而希望在本节课后面再回解该问题。第四环节:练习随堂练习 (体现建立直角坐标系的多样性)第五环节:小结内容:小结本节课自己的收获和进步,从知识和能力上两个方面总结,老师予于肯定和鼓励。 目的:鼓励学生大胆发言,敢于表达自己的观点,同时学生之间可以相互学习,共同提高,老师给予肯定和鼓励,激发学生的学习热情。
作业 课本习题5.5
后记
课 时 教 案
第 周 星期 第 节 年 月 日
课 题 3. 轴对称与坐标变化
教 学 目 标 1、在同一直角坐标系中,感受图形上点的坐标变化与图形的轴对称变换之间的关系. 2、经历图形坐标变化与图形轴对称之间关系的探索过程,发展形象思维能力和数形结合意识。3.经历探究物体与图形的形状、大小、位置关系和变换的过程,掌握空间与图形的基础知识和基本技能,培养学生的探索能力。
教 材 分析 重 点 经历图形坐标变化与图形轴对称之间关系的探索过程,明确图形坐标变化与图形轴对称之间关系。
难 点 由坐标的变化探索新旧图形之间的变化探索过程,发展形象思维能力和数形结合意识。
教 具 电脑、投影仪 二次备课
教 学 过 程 第一环节 创设问题情境,引入新课『师』:在前几节课中我们学习了平面直角坐标系的有关知识,会画平面直角坐标系;能在方格纸上建立适当的直角坐标系,描述物体的位置;在给定的直角坐标系下,会根据坐标描出点的位置,由点的位置写出它的坐标。 我们知道点的位置不同写出的坐标就不同,反过来,不同的坐标确定不同的点。如果坐标中的横(纵)坐标不变,纵(横)坐标按一定的规律变化,或者横纵坐标都按一定的规律变化,那么图形是否会变化,变化的规律是怎样的,这将是本节课中我们要研究的问题。 探索两个关于坐标轴对称的图形的坐标关系1.在如图所示的平面直角坐标系中,第一、二象限内各有一面小旗。 两面小旗之间有怎样的位置关系?对应点A与A1的坐标又有什么特点?其它对应的点也有这个特点吗? 2.在右边的坐标系内,任取一点,做出这个点关于y轴对称的点,看看两个点的坐标有什么样的位置关系,说说其中的道理。 3.如果关于x轴对称呢? 在这个坐标系里作出小旗ABCD关于x轴的对称图形,它的各个顶点的坐标与原来的点的坐标有什么关系?
教 学 过 程 4.关于x轴对称的两点,它们的横坐标 ,纵坐标 ; 关于y轴对称的两点,它们的横坐标 ,纵坐标 。 5.已知点P(2a-3,3),点A(-1,3b+2), (1)如果点P与点A关于x轴对称,那么a+b= ; (2)如果点P与点A关于y轴对称,那么a+b= 。 拿出方格纸,并在方格纸上建立直角坐标系,根据我读出的点的坐标在纸上找到相应的点,并依次用线段将这些点连接起来。坐标是(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)。 观察所得的图形,你们觉得它像什么? 下面我们把坐标适当地作些变化,这条鱼就能变大或变胖,即变化的鱼。第二环节 探究新知:例1 将上图中的点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)做以下变化: (1)纵坐标保持不变,横坐标分别乘以-1,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化? (2)横坐标保持不变,纵坐标分别乘以-1,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化? (3)横坐标、纵坐标都分别乘以-1,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?第三环节 拓展练习:1.点 A(2,- 3)关 于 x 轴 对 称 的 点 的 坐 标 是( ).
2.点 B( - 2,1)关 于 y 轴 对 称 的 点 的 坐 标 是( ). 3.点(4,3)与点(4,- 3)的关系是( ) . A.关于原点对称 B.关于 x轴对称
C.关于 y轴对称 D.不能构成对称关系
4.点(m,- 1)和点(2,n)关于 x轴对称,则 mn等于( ) A.- 2 B.2 C.1 D.- 1 5.(1)若 mn = 0,则点 P(m,n)必定在 上.
(2)已知点 P( a,b),Q(3,6),且 PQ ∥ x轴,则b的值为 . 第四环节 课堂小结1、关于y轴对称的两个图形上点的坐标特征:(x , y)——(- x , y)2、关于x轴对称的两个图形上点的坐标特征:(x , y)——(x , - y)3、关于原点对称的两个图形上点的坐标特征:(x , y)——(- x , -y)
作业 习题3.5 1,2,3
后记 教学中务必给学生创造自主学习与合作交流的机会,留给学生充足的动手机会和思考空间,教师不要急于下结论。事先一定要准备好坐标纸等,提高课堂效率。
课 时 教 案
第 周 星期 第 节 年 月 日
课 题 《位置与坐标》回顾与思考
教 学 目 标 从现实生活中体会确定位置的不同方式与方法,感受确定位置的多样性; 掌握利用直角坐标系确定位置的方法; 会用平面直角坐标系来解决一些简单的实际问题;
教 材 分析 重 点 掌握利用直角坐标系确定位置的方法;
难 点 会用平面直角坐标系来解决一些简单的
教 具 电脑、投影仪 二次备课
教 学 过 程 学习过程 活动1 知识梳理1、在平面内,确定点的位置一般需要几个数据?举例说明。 2、平面直角坐标系中,如何确定给定点的坐标?给定坐标,如何确定对应的点?分别举例说明。 3、平面直角坐标系中,坐标轴上的点具有什么特点?平行于坐标轴的线段上的点,它们的坐标之间有什么样的关系?分别举例说明。 4.平面直角坐标系中,关于坐标轴对称的点的坐标之间具有怎样的关系?反过来坐标具有这样的关系的点关于坐标轴对称吗?这些结论可以帮助你解决哪些问题? 5、通过上述知识的回顾,请你整理出本章的知识框架图:活动2:典型例析例1.右图是某市几个旅游景点的示意图(图中每个小正方形的边长为1个单位长度)。 请以某景点为原点,画出直角坐标系,并用坐标表示出下列景点的位置:光岳楼___________、 湖心岛___________、金凤广场__________、动物园___________。
教 学 过 程 反思。交流与同伴比较,你们得到的各个景点的坐标一样吗?判断各自的做法是否正确,说说出现差异的原因。例2.已知平面直角坐标系上有六个点: 请将上述六个点按下列要求分成两类,并写出同类点具有而另一类点不具有的一个特征(请将答案按要求写在横线上,点用字母表示). ⑴甲类含两个点,乙类含其余四个点. 甲类:点____,____是同一类点,其特征是__ ___; 乙类:点____,____,____,____是同一类点,其特征是__ ____; ⑵甲类含三个点,乙类含其余三个点. 甲类:点___,___,____是同一类点,其特征是__ _____; 乙类:点___,___,____是同一类点,其特征是___ ____.反思交流你们的结果一样吗?关于分类,你们有哪些经验?与同伴交流。例3.如图,已知A、B两村庄的坐标分别为(2,2)、(7,4),一辆汽车在轴上行驶,从原点O出发。 (1)汽车行驶到什么位置时离A村最近?写出此点的坐标。(2)汽车行驶到什么位置时离B村最近?写出此点的坐标。*(3)汽车行驶到什么位置时,距离两村的和最短?请在图中画出这个位置,并求出此时汽车到两村距离的和。活动3:自主反馈1(1)如图,正八边形的边长为2,点C的坐标是(,0)写出其余各点的坐标:(2)如果在(1)中做出正八边形关于x轴对称的图形,则可以得到一个“8”字形,试尽快写出这个“8”字形另外六个顶点的坐标。 (3)试换一个点为原点,建立另一个坐标系,并写出各个顶点的坐标。
作业
后记
A
B
C
D
O
H
G
E
F
x
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
