第三章3.3三视图练习试卷
图片预览


文档简介
3.3 三视图
第1课时 由几何体到三视图
基础题
知识点 三视图
1.(2017·邵阳)下列立体图形中,主视图是圆的是(A)
A B C D
2.如图,下列几何体的左视图不是矩形的是(B)
3.(2018·嘉兴)下列几何体中,俯视图为三角形的是(C)
4.有一种圆柱体茶叶筒如图所示,则它的主视图是(D)
5.(2018·黄石)如图,该几何体的俯视图是(A)
6.(2018·菏泽)如图是两个等直径圆柱构成的“T”形管道,其左视图是(B)
7.(2017·泰安)下面三个几何体:
其中俯视图是四边形的几何体个数是(B)
A.1 B.2 C.3 D.0
8.下列几何体中,其主视图、左视图、俯视图中的图形只有两个相同的是(D)
A.正方体 B.球 C.直三棱柱 D.圆柱
9.图中物体的一个视图(a)的名称为主视图.
10.(教材P108练习T1变式)画出图中正三棱柱的主视图、左视图、俯视图.
解:如图所示:
中档题
11.(2017·丽水)如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是(B)
A.俯视图与主视图相同
B.左视图与主视图相同
C.左视图与俯视图相同
D.三个视图都相同
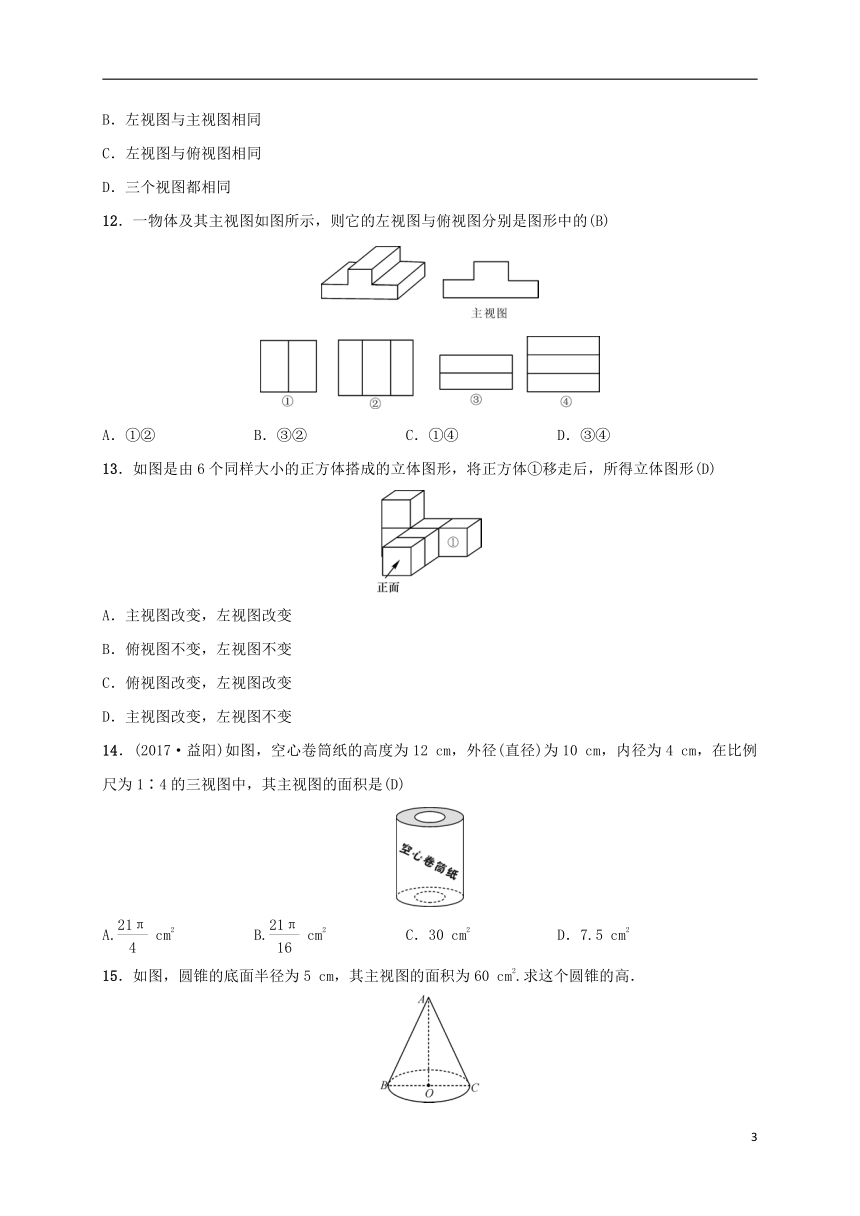
12.一物体及其主视图如图所示,则它的左视图与俯视图分别是图形中的(B)
A.①② B.③② C.①④ D.③④
13.如图是由6个同样大小的正方体搭成的立体图形,将正方体①移走后,所得立体图形(D)
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图改变,左视图改变
D.主视图改变,左视图不变
14.(2017·益阳)如图,空心卷筒纸的高度为12 cm,外径(直径)为10 cm,内径为4 cm,在比例尺为1∶4的三视图中,其主视图的面积是(D)
A. cm2 B. cm2 C.30 cm2 D.7.5 cm2
15.如图,圆锥的底面半径为5 cm,其主视图的面积为60 cm2.求这个圆锥的高.
解:该圆锥的主视图为等腰△ABC,底边BC=2×5=10(cm).
∵S△ABC=BC·AO=60 cm2,
∴AO==12(cm),即这个圆锥的高为12 cm.
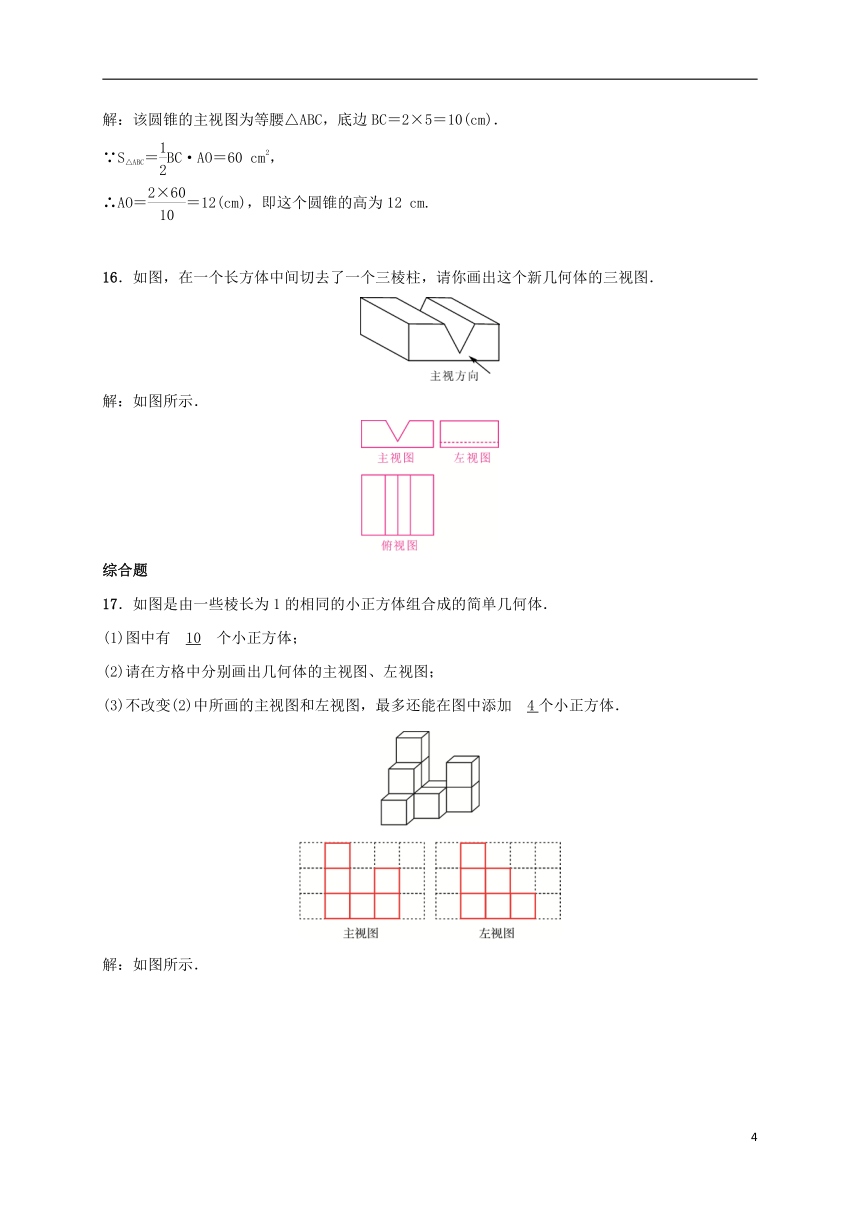
16.如图,在一个长方体中间切去了一个三棱柱,请你画出这个新几何体的三视图.
解:如图所示.
综合题
17.如图是由一些棱长为1的相同的小正方体组合成的简单几何体.
(1)图中有 10 个小正方体;
(2)请在方格中分别画出几何体的主视图、左视图;
(3)不改变(2)中所画的主视图和左视图,最多还能在图中添加 4个小正方体.
解:如图所示.
第2课时 由三视图到几何体
基础题
知识点 由三视图判断几何体
1.(2017·长沙)某几何体的三视图如图所示,则此几何体是(B)
A.长方形
B.圆柱
C.球
D.正三棱柱
2.(2018·襄阳)一个几何体的三视图如图所示,那么该几何体是(C)
A B C D
3.一个几何体的三视图完全相同,该几何体可以是(D)
A.圆锥 B.圆柱
C.长方体 D.球
4.与如图所示的三视图对应的几何体是(B)
A B C D
5.若某几何体的三视图如图所示,则这个几何体是(C)
6.一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为8.
左视图 俯视图
7.(教材P116复习题T5变式)如图是一个用相同的小立方块搭成的几何体的三视图,则组成这个几何体的小立方块的个数是4个.
8.根据如图所示几何体的三视图描述物体的形状.
解:几何体的形状为:
9.如图为一几何体的三视图:
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种表面展开图.
解:(1)正三棱柱.
(2)如图.
中档题
10.一天小明的爸爸送给小明一个礼物,小明打开包装后,利用所学的知识画出了它的主视图和俯视图分别如图所示,根据小明所画的三视图,猜测小明的爸爸送给小明的礼物可能是(B)
A.钢笔 B.生日蛋糕 C.光盘 D.一套衣服
11.如图是由几个相同的小正方体搭成的几何体的主视图和俯视图,组成这个几何体的小正方体的个数是(B)
A.5或6 B.6或7 C.7或8 D.8或9
12.(2018·孝感)如图是一个几何体的三视图(图中尺寸单位:cm),根据图中数据计算,这个几何体的表面积为16πcm2.
13.(教材P110例5变式)如图是一个零件的三视图,试描述出这个零件的形状.
解:这个零件由两部分组成,上面是一个圆锥,下面是一个圆柱,圆锥在圆柱的中央.
14.一个零件的主视图、左视图、俯视图如图所示(尺寸单位:厘米).
(1)这个零件是什么几何体?
(2)求这个零件的表面积、体积.(结果保留π)
解:(1)这个零件是圆柱体.
(2)表面积为π×52×2+15×π×10=200π(平方厘米),
体积为π×52×15=375π(立方厘米).
综合题
15.某工厂要加工一批密封罐,设计者给出了它的三视图,请你根据如图所示的三视图确定制作每个罐所需钢板的面积.(单位:mm2,精确到1 mm2)
解:每个底面面积可以看成6个边长为50 mm的正三角形的面积和,
即S底=6××50×50×(mm2),
侧面面积等于6个边长为50 mm的正方形的面积的和,
即S侧=6×50×50(mm2),
∴制作一个密封罐所需钢板的面积为6×50×50+2×6××50×50×=6×502×(1+)≈27 990(mm2).
第1课时 由几何体到三视图
基础题
知识点 三视图
1.(2017·邵阳)下列立体图形中,主视图是圆的是(A)
A B C D
2.如图,下列几何体的左视图不是矩形的是(B)
3.(2018·嘉兴)下列几何体中,俯视图为三角形的是(C)
4.有一种圆柱体茶叶筒如图所示,则它的主视图是(D)
5.(2018·黄石)如图,该几何体的俯视图是(A)
6.(2018·菏泽)如图是两个等直径圆柱构成的“T”形管道,其左视图是(B)
7.(2017·泰安)下面三个几何体:
其中俯视图是四边形的几何体个数是(B)
A.1 B.2 C.3 D.0
8.下列几何体中,其主视图、左视图、俯视图中的图形只有两个相同的是(D)
A.正方体 B.球 C.直三棱柱 D.圆柱
9.图中物体的一个视图(a)的名称为主视图.
10.(教材P108练习T1变式)画出图中正三棱柱的主视图、左视图、俯视图.
解:如图所示:
中档题
11.(2017·丽水)如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是(B)
A.俯视图与主视图相同
B.左视图与主视图相同
C.左视图与俯视图相同
D.三个视图都相同
12.一物体及其主视图如图所示,则它的左视图与俯视图分别是图形中的(B)
A.①② B.③② C.①④ D.③④
13.如图是由6个同样大小的正方体搭成的立体图形,将正方体①移走后,所得立体图形(D)
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图改变,左视图改变
D.主视图改变,左视图不变
14.(2017·益阳)如图,空心卷筒纸的高度为12 cm,外径(直径)为10 cm,内径为4 cm,在比例尺为1∶4的三视图中,其主视图的面积是(D)
A. cm2 B. cm2 C.30 cm2 D.7.5 cm2
15.如图,圆锥的底面半径为5 cm,其主视图的面积为60 cm2.求这个圆锥的高.
解:该圆锥的主视图为等腰△ABC,底边BC=2×5=10(cm).
∵S△ABC=BC·AO=60 cm2,
∴AO==12(cm),即这个圆锥的高为12 cm.
16.如图,在一个长方体中间切去了一个三棱柱,请你画出这个新几何体的三视图.
解:如图所示.
综合题
17.如图是由一些棱长为1的相同的小正方体组合成的简单几何体.
(1)图中有 10 个小正方体;
(2)请在方格中分别画出几何体的主视图、左视图;
(3)不改变(2)中所画的主视图和左视图,最多还能在图中添加 4个小正方体.
解:如图所示.
第2课时 由三视图到几何体
基础题
知识点 由三视图判断几何体
1.(2017·长沙)某几何体的三视图如图所示,则此几何体是(B)
A.长方形
B.圆柱
C.球
D.正三棱柱
2.(2018·襄阳)一个几何体的三视图如图所示,那么该几何体是(C)
A B C D
3.一个几何体的三视图完全相同,该几何体可以是(D)
A.圆锥 B.圆柱
C.长方体 D.球
4.与如图所示的三视图对应的几何体是(B)
A B C D
5.若某几何体的三视图如图所示,则这个几何体是(C)
6.一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为8.
左视图 俯视图
7.(教材P116复习题T5变式)如图是一个用相同的小立方块搭成的几何体的三视图,则组成这个几何体的小立方块的个数是4个.
8.根据如图所示几何体的三视图描述物体的形状.
解:几何体的形状为:
9.如图为一几何体的三视图:
(1)写出这个几何体的名称;
(2)任意画出这个几何体的一种表面展开图.
解:(1)正三棱柱.
(2)如图.
中档题
10.一天小明的爸爸送给小明一个礼物,小明打开包装后,利用所学的知识画出了它的主视图和俯视图分别如图所示,根据小明所画的三视图,猜测小明的爸爸送给小明的礼物可能是(B)
A.钢笔 B.生日蛋糕 C.光盘 D.一套衣服
11.如图是由几个相同的小正方体搭成的几何体的主视图和俯视图,组成这个几何体的小正方体的个数是(B)
A.5或6 B.6或7 C.7或8 D.8或9
12.(2018·孝感)如图是一个几何体的三视图(图中尺寸单位:cm),根据图中数据计算,这个几何体的表面积为16πcm2.
13.(教材P110例5变式)如图是一个零件的三视图,试描述出这个零件的形状.
解:这个零件由两部分组成,上面是一个圆锥,下面是一个圆柱,圆锥在圆柱的中央.
14.一个零件的主视图、左视图、俯视图如图所示(尺寸单位:厘米).
(1)这个零件是什么几何体?
(2)求这个零件的表面积、体积.(结果保留π)
解:(1)这个零件是圆柱体.
(2)表面积为π×52×2+15×π×10=200π(平方厘米),
体积为π×52×15=375π(立方厘米).
综合题
15.某工厂要加工一批密封罐,设计者给出了它的三视图,请你根据如图所示的三视图确定制作每个罐所需钢板的面积.(单位:mm2,精确到1 mm2)
解:每个底面面积可以看成6个边长为50 mm的正三角形的面积和,
即S底=6××50×50×(mm2),
侧面面积等于6个边长为50 mm的正方形的面积的和,
即S侧=6×50×50(mm2),
∴制作一个密封罐所需钢板的面积为6×50×50+2×6××50×50×=6×502×(1+)≈27 990(mm2).
