第二章2.2圆心角圆周角练习试卷
图片预览



文档简介
2.2 圆心角、圆周角
2.2.1 圆心角
基础题
知识点1 认识圆心角
1.下面四个图中的角,是圆心角的是(D)
A B C D
2.将一个圆分成四个扇形,它们的圆心角的度数比为4∶4∶5∶7,则这四个扇形中,圆心角最大的是(D)
A.54° B.72° C.90° D.126°
知识点2 圆心角、弧、弦之间的关系
3.下列说法中,正确的是(B)
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等所对的圆心角相等
4.如图,在⊙O中,=,∠AOB=122°,则∠AOC的度数为(A)
A.122° B.120° C.61° D.58°
5.如图,A,B,C,D是⊙O上的四点,且AD=BC,则AB与CD的大小关系为(B)
A.AB>CD B.AB=CD
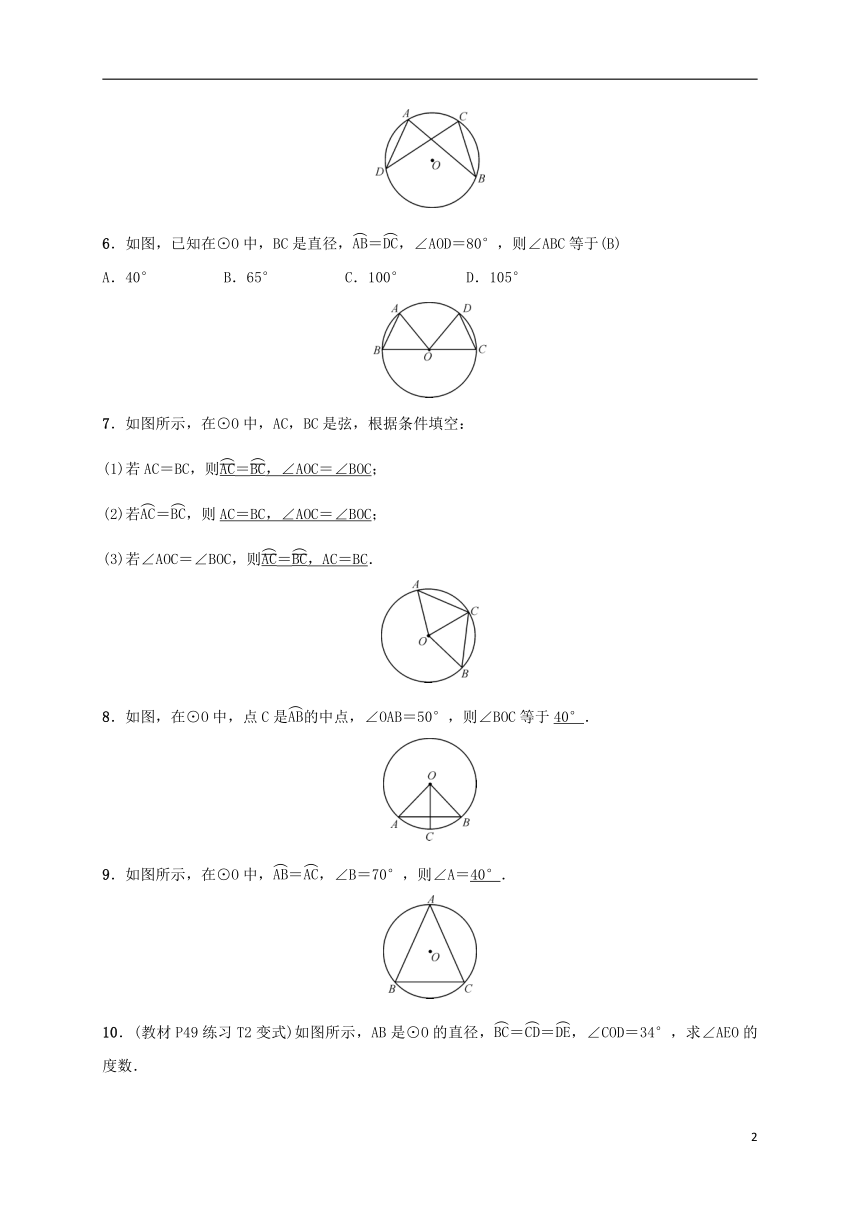
C.AB6.如图,已知在⊙O中,BC是直径,=,∠AOD=80°,则∠ABC等于(B)
A.40° B.65° C.100° D.105°
7.如图所示,在⊙O中,AC,BC是弦,根据条件填空:
(1)若AC=BC,则=,∠AOC=∠BOC;
(2)若=,则AC=BC,∠AOC=∠BOC;
(3)若∠AOC=∠BOC,则=,AC=BC.
8.如图,在⊙O中,点C是的中点,∠OAB=50°,则∠BOC等于40°.
9.如图所示,在⊙O中,=,∠B=70°,则∠A=40°.
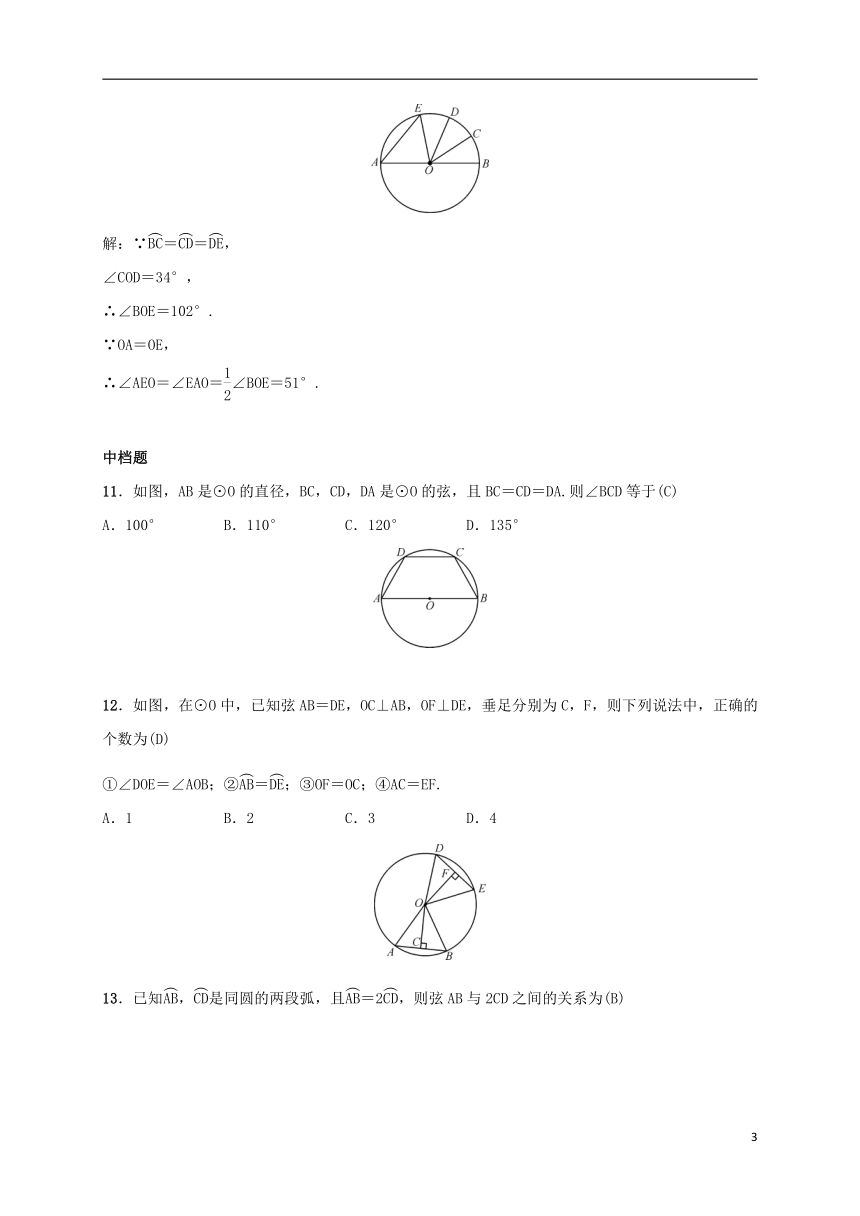
10.(教材P49练习T2变式)如图所示,AB是⊙O的直径,==,∠COD=34°,求∠AEO的度数.
解:∵==,
∠COD=34°,
∴∠BOE=102°.
∵OA=OE,
∴∠AEO=∠EAO=∠BOE=51°.
中档题
11.如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA.则∠BCD等于(C)
A.100° B.110° C.120° D.135°
12.如图,在⊙O中,已知弦AB=DE,OC⊥AB,OF⊥DE,垂足分别为C,F,则下列说法中,正确的个数为(D)
①∠DOE=∠AOB;②=;③OF=OC;④AC=EF.
A.1 B.2 C.3 D.4
13.已知,是同圆的两段弧,且=2,则弦AB与2CD之间的关系为(B)
A.AB=2CD
B.AB<2CD
C.AB>2CD
D.不能确定
提示:如图,在圆上截取=,连接DE,CE,则有=.∴AB=CE.又CD+DE=2CD>CE=AB,∴AB<2CD,故选B.
14.如图,A,B,C是⊙O上的三点,且有==.
(1)求∠AOB,∠BOC,∠AOC的度数;
(2)连接AB,BC,CA,试确定△ABC的形状.
解:(1)∵==,
∴∠AOB=∠BOC=∠AOC.
又∵∠AOB+∠BOC+∠COA=360°,
∴∠AOB=∠BOC=∠AOC=120°.
(2)∵==,
∴AB=BC=CA.
∴△ABC是等边三角形.
15.如图,AB,CD是⊙O的两条直径,过点A作AE∥CD交⊙O于点E,连接BD,DE,求证:BD=DE.
证明:连接OE,
∵OA=OE,
∴∠A=∠OEA.
∵AE∥CD,
∴∠BOD=∠A,∠DOE=∠OEA.
∴∠BOD=∠DOE.
∴BD=DE.
16.如图,已知AB是⊙O的直径,M,N分别是AO,BO的中点,CM⊥AB,DN⊥AB.求证:=.
证明:连接OC,OD,
∵AB是⊙O的直径,M,N分别是AO,BO的中点,
∴OM=ON.
∵CM⊥AB,DN⊥AB,
∴∠OMC=∠OND=90°.
在Rt△OMC和Rt△OND中,
∴Rt△OMC≌Rt△OND(HL).
∴∠COM=∠DON.
∴=.
综合题
17.如图,在⊙O中,AB,CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为E,F.
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么与的大小有什么关系?为什么?
解:(1)OE=OF.理由:
∵OE⊥AB,OF⊥CD,OA=OB,OC=OD,
∴∠OEB=∠OFD=90°,∠EOB=∠AOB,∠FOD=∠COD.
∵∠AOB=∠COD,∴∠EOB=∠FOD.
在△EOB和△FOD中,
∴△EOB≌△FOD(AAS).
∴OE=OF.
(2)=.
理由:∵OE⊥AB,OF⊥CD,AO=BO,CO=DO,
∴∠OEB=∠OFD=90°.
∴点E,F分别是AB,CD的中点.
在Rt△BEO和Rt△DFO中,
∴Rt△BEO≌Rt△DFO(HL).
∴BE=DF.
∵AB=2BE,CD=2DF,
∴AB=CD.
∴=.
2.2.2 圆周角
第1课时 圆周角定理及其推论1
基础题
知识点1 认识圆周角
1.下列四个图中,∠x是圆周角的是(C)
知识点2 圆周角定理
2.(2018·衢州)如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度数是(B)
A.75° B.70° C.65° D.35°
3.如图,△ABC内接于⊙O.若∠A=α,则∠OBC等于(D)
A.180°-2α B.2α
C.90°+α D.90°-α
4.如图,将直角三角板60°角的顶点放在圆心O上,斜边和一直角边分别与⊙O相交于A,B两点,P是优弧AB上任意一点(与A,B不重合),则∠APB=30°.
5.(2018·广东)在同圆中,已知弧AB所对的圆心角是100°,则弧AB所对的圆周角是50°.
知识点3 圆周角定理推论1
6.如图,点A,B,C,D都在⊙O上,AC,BD相交于点E,则∠ABD=(A)
A.∠ACD B.∠ADB
C.∠AED D.∠ACB
7.如图,已知AB,CD是⊙O的两条直径,∠ABC=28°,那么∠BAD=(A)
A.28° B.42° C.56° D.84°
8.(教材P52练习T3变式)如图,在⊙O中,弦AB,CD相交于点P.若∠A=30°,∠APD=70°,则∠B等于(C)
A.30° B.35° C.40° D.50°
9.如图,BD是⊙O的直径,点A,C在⊙O上,=,∠AOB=60°,则∠BDC的度数是(D)
A.60° B.45° C.35° D.30°
10.如图所示,弦AB,CD相交于点O,连接AD,BC,在不添加辅助线的情况下,请在图中找出一对相等的角,它们是答案不唯一,如:∠A=∠C,∠B=∠D,∠AOD=∠BOC,∠AOC=∠BOD.
11.如图,已知A,B,C,D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD,AD.求证:DB平分∠ADC.
证明:∵AB=BC,
∴=.
∴∠BDC=∠ADB.
∴DB平分∠ADC.
易错点 忽略弦所对的圆周角不唯一而致错
12.已知某个圆的弦长等于它的半径,则这条弦所对的圆周角的度数为30°或150°.
中档题
13.如图,P是⊙O外一点,PA,PB分别交⊙O于C,D两点,已知和所对的圆心角分别为90°和50°,则∠P=(D)
A.45° B.40° C.25° D.20°
14.(2018·菏泽)如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA等于(D)
A.64° B.58° C.32° D.26°
15.如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正弦值等于.
16.如图所示,在⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为50°.
17.(教材P52练习T3变式)如图,在⊙O中,A,B是圆上的两点,已知∠AOB=40°,直径CD∥AB,连接AC,则∠BAC=35°.
18.如图,点A,B,C三点在⊙O上,过C作CD∥AB与⊙O相交于D点,E是上一点,且满足AD=DE,连接BD与AE相交于点F.求证:△AFD∽△ABC.
证明:∵AB∥CD,
∴∠BAC=∠ACD.
∵AD=DE,∴=.
∴∠DAE=∠AED.
∴∠DAE=∠AED=∠ACD=∠BAC.
∵∠ADF=∠ACB,∠DAE=∠BAC,
∴△AFD∽△ABC.
综合题
19.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状,并证明你的结论;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论.
证明:(1)△ABC是等边三角形.
在⊙O中,
∵∠BAC与∠CPB是所对的圆周角,
∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC.
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°.
∴△ABC为等边三角形.
(2)在PC上截取PD=AP,连接AD,
∵∠APC=60°,
∴△APD是等边三角形.
∴AD=AP=PD,∠ADP=60°,
即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB.
在△APB和△ADC中,
∴△APB≌△ADC(AAS).
∴BP=CD.
又∵PD=AP.
∴CP=CD+PD=BP+AP.
第2课时 圆周角定理推论2及圆内接四边形的性质
基础题
知识点1 圆周角定理推论2
1.(2017·福建)如图,AB是⊙O的直径,C,D是⊙O上位于AB异侧的两点.则下列四个角中,一定与∠ACD互余的角是(D)
A.∠ADC B.∠ABD
C.∠BAC D.∠BAD
2.如图,小华同学设计了一个量直径的测量器,标有刻度的尺子OA,OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位长度,OF=6个单位长度,则圆的直径为(B)
A.12个单位长度 B.10个单位长度
C.4个单位长度 D.15个单位长度
3.如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为(C)
A.20° B.40° C.50° D.70°
4.如图,CD是⊙O的直径,已知∠1=30°,则∠2=(C)
A.30° B.45° C.60° D.70°
5.如图,把直角三角形的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M,N,量得OM=8 cm,ON=6 cm,则该圆玻璃镜的半径是(B)
A. cm
B.5 cm
C.6 cm
D.10 cm
6.如图,AB是⊙O的直径,点D在⊙O上,∠AOD=130°,BC∥OD交⊙O于C,求∠A的度数.
解:∵∠AOD=130°,
∴∠BOD=50°.
∵BC∥OD,∴∠B=∠BOD=50°.
∵AB是⊙O的直径,
∴∠ACB=90°.
∴∠A=90°-∠B=40°.
知识点2 圆内接四边形对角互补
7.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点.若∠BAD=105°,则∠DCE的大小是(B)
A.115° B.105° C.100° D.95°
8.(教材P55例4变式)(2018·邵阳)如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是(B)
A.80° B.120° C.100° D.90°
9.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD=110°,则∠BAD=70°.
10.如图,已知∠EAD是圆内接四边形ABCD的一个外角,并且BD=DC.求证:AD平分∠EAC.
证明:∵∠EAD+∠BAD=180°,∠DCB+∠BAD=180°,
∴∠EAD=∠DCB.
∵BD=DC,∴∠DBC=∠DCB.
又∵∠DBC=∠DAC,
∴∠EAD=∠DAC,即AD平分∠EAC.
易错点 对圆内接四边形的概念理解不清导致错误
11.如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=110°,则∠α=140°.
中档题
12.在圆内接四边形ABCD中,若∠A∶∠B∶∠C=1∶2∶5,则∠D等于(B)
A.60° B.120° C.140° D.150°
13.如图,AB为⊙O的直径,关于角p,q,r,s之间的关系:①p=2q;②q=r;③p+s=180°中,正确的是(A)
A.只有①和② B.只有①和③
C.只有②和③ D.①②③
14.(2018·白银)如图,⊙A过点O(0,0),C(,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是(B)
A.15° B.30° C.45° D.60°
15.(2018·北京)如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB=70°.
16.如图,已知点A,B,C,D均在⊙O上,CD为∠ACE的平分线.
(1)求证:△ABD为等腰三角形;
(2)若∠DCE=45°,BD=6,求⊙O的半径.
解:(1)证明:
∵CD平分∠ECA,
∴∠ECD=∠DCA.
∵∠ECD+∠DCB=180°,∠DCB+∠BAD=180°,
∴∠ECD=∠DAB.
又∵∠DCA=∠DBA,
∴∠DBA=∠DAB.
∴DB=DA.
∴△ABD是等腰三角形.
(2)∵∠DCE=∠DCA=45°,
∴∠ECA=∠ACB=90°.
∴∠BDA=90°.∴AB是直径.
∵BD=AD=6,
∴AB===6.
∴⊙O的半径为3.
17.(2018·宜昌)如图,在△ABC中,AB=AC.以AB为直径的半圆交AC于点D,交BC于点E.延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.
解:(1)证明:∵AB为半圆的直径,
∴∠AEB=90°,
∵AB=AC,
∴CE=BE.
又∵EF=AE,
∴四边形ABFC是平行四边形.
又∵AB=AC,(或∠AEB=90°)
∴平行四边形ABFC是菱形.
(2)连接BD.
∵AD=7,BE=CE=2,
设CD=x,则AB=AC=7+x.
∵AB为半圆的直径,
∴∠ADB=90°.
∴AB2-AD2=CB2-CD2.
∴(7+x)2-72=42-x2.
∴x1=1或x2=-8(舍去).
∴S半圆=×π×42=8π.
∴BD=.
∴S菱形ABFC=8.
综合题
18.如图,在⊙O中,直径AB的两侧有定点C和动点P,点P在上运动(不与A,B重合),过点C作CP的垂线,与PB的延长线交于点Q.
(1)试猜想:△PCQ与△ACB具有何种关系?(不要求证明)
(2)当点P运动到什么位置时,△ABC≌△PCB?并给出证明.
解:(1)△PCQ∽△ACB.
(2)当为半圆时,
△ABC≌△PCB.
证明:∵AB是直径,
∴∠ACB=90°.
∵为半圆,
∴CP是直径.
∴∠PBC=90°,AB=CP.
∵CB是公共边,∴Rt△ABC≌Rt△PCB(HL).
2.2.1 圆心角
基础题
知识点1 认识圆心角
1.下面四个图中的角,是圆心角的是(D)
A B C D
2.将一个圆分成四个扇形,它们的圆心角的度数比为4∶4∶5∶7,则这四个扇形中,圆心角最大的是(D)
A.54° B.72° C.90° D.126°
知识点2 圆心角、弧、弦之间的关系
3.下列说法中,正确的是(B)
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等所对的圆心角相等
4.如图,在⊙O中,=,∠AOB=122°,则∠AOC的度数为(A)
A.122° B.120° C.61° D.58°
5.如图,A,B,C,D是⊙O上的四点,且AD=BC,则AB与CD的大小关系为(B)
A.AB>CD B.AB=CD
C.AB
A.40° B.65° C.100° D.105°
7.如图所示,在⊙O中,AC,BC是弦,根据条件填空:
(1)若AC=BC,则=,∠AOC=∠BOC;
(2)若=,则AC=BC,∠AOC=∠BOC;
(3)若∠AOC=∠BOC,则=,AC=BC.
8.如图,在⊙O中,点C是的中点,∠OAB=50°,则∠BOC等于40°.
9.如图所示,在⊙O中,=,∠B=70°,则∠A=40°.
10.(教材P49练习T2变式)如图所示,AB是⊙O的直径,==,∠COD=34°,求∠AEO的度数.
解:∵==,
∠COD=34°,
∴∠BOE=102°.
∵OA=OE,
∴∠AEO=∠EAO=∠BOE=51°.
中档题
11.如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA.则∠BCD等于(C)
A.100° B.110° C.120° D.135°
12.如图,在⊙O中,已知弦AB=DE,OC⊥AB,OF⊥DE,垂足分别为C,F,则下列说法中,正确的个数为(D)
①∠DOE=∠AOB;②=;③OF=OC;④AC=EF.
A.1 B.2 C.3 D.4
13.已知,是同圆的两段弧,且=2,则弦AB与2CD之间的关系为(B)
A.AB=2CD
B.AB<2CD
C.AB>2CD
D.不能确定
提示:如图,在圆上截取=,连接DE,CE,则有=.∴AB=CE.又CD+DE=2CD>CE=AB,∴AB<2CD,故选B.
14.如图,A,B,C是⊙O上的三点,且有==.
(1)求∠AOB,∠BOC,∠AOC的度数;
(2)连接AB,BC,CA,试确定△ABC的形状.
解:(1)∵==,
∴∠AOB=∠BOC=∠AOC.
又∵∠AOB+∠BOC+∠COA=360°,
∴∠AOB=∠BOC=∠AOC=120°.
(2)∵==,
∴AB=BC=CA.
∴△ABC是等边三角形.
15.如图,AB,CD是⊙O的两条直径,过点A作AE∥CD交⊙O于点E,连接BD,DE,求证:BD=DE.
证明:连接OE,
∵OA=OE,
∴∠A=∠OEA.
∵AE∥CD,
∴∠BOD=∠A,∠DOE=∠OEA.
∴∠BOD=∠DOE.
∴BD=DE.
16.如图,已知AB是⊙O的直径,M,N分别是AO,BO的中点,CM⊥AB,DN⊥AB.求证:=.
证明:连接OC,OD,
∵AB是⊙O的直径,M,N分别是AO,BO的中点,
∴OM=ON.
∵CM⊥AB,DN⊥AB,
∴∠OMC=∠OND=90°.
在Rt△OMC和Rt△OND中,
∴Rt△OMC≌Rt△OND(HL).
∴∠COM=∠DON.
∴=.
综合题
17.如图,在⊙O中,AB,CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为E,F.
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么与的大小有什么关系?为什么?
解:(1)OE=OF.理由:
∵OE⊥AB,OF⊥CD,OA=OB,OC=OD,
∴∠OEB=∠OFD=90°,∠EOB=∠AOB,∠FOD=∠COD.
∵∠AOB=∠COD,∴∠EOB=∠FOD.
在△EOB和△FOD中,
∴△EOB≌△FOD(AAS).
∴OE=OF.
(2)=.
理由:∵OE⊥AB,OF⊥CD,AO=BO,CO=DO,
∴∠OEB=∠OFD=90°.
∴点E,F分别是AB,CD的中点.
在Rt△BEO和Rt△DFO中,
∴Rt△BEO≌Rt△DFO(HL).
∴BE=DF.
∵AB=2BE,CD=2DF,
∴AB=CD.
∴=.
2.2.2 圆周角
第1课时 圆周角定理及其推论1
基础题
知识点1 认识圆周角
1.下列四个图中,∠x是圆周角的是(C)
知识点2 圆周角定理
2.(2018·衢州)如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度数是(B)
A.75° B.70° C.65° D.35°
3.如图,△ABC内接于⊙O.若∠A=α,则∠OBC等于(D)
A.180°-2α B.2α
C.90°+α D.90°-α
4.如图,将直角三角板60°角的顶点放在圆心O上,斜边和一直角边分别与⊙O相交于A,B两点,P是优弧AB上任意一点(与A,B不重合),则∠APB=30°.
5.(2018·广东)在同圆中,已知弧AB所对的圆心角是100°,则弧AB所对的圆周角是50°.
知识点3 圆周角定理推论1
6.如图,点A,B,C,D都在⊙O上,AC,BD相交于点E,则∠ABD=(A)
A.∠ACD B.∠ADB
C.∠AED D.∠ACB
7.如图,已知AB,CD是⊙O的两条直径,∠ABC=28°,那么∠BAD=(A)
A.28° B.42° C.56° D.84°
8.(教材P52练习T3变式)如图,在⊙O中,弦AB,CD相交于点P.若∠A=30°,∠APD=70°,则∠B等于(C)
A.30° B.35° C.40° D.50°
9.如图,BD是⊙O的直径,点A,C在⊙O上,=,∠AOB=60°,则∠BDC的度数是(D)
A.60° B.45° C.35° D.30°
10.如图所示,弦AB,CD相交于点O,连接AD,BC,在不添加辅助线的情况下,请在图中找出一对相等的角,它们是答案不唯一,如:∠A=∠C,∠B=∠D,∠AOD=∠BOC,∠AOC=∠BOD.
11.如图,已知A,B,C,D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD,AD.求证:DB平分∠ADC.
证明:∵AB=BC,
∴=.
∴∠BDC=∠ADB.
∴DB平分∠ADC.
易错点 忽略弦所对的圆周角不唯一而致错
12.已知某个圆的弦长等于它的半径,则这条弦所对的圆周角的度数为30°或150°.
中档题
13.如图,P是⊙O外一点,PA,PB分别交⊙O于C,D两点,已知和所对的圆心角分别为90°和50°,则∠P=(D)
A.45° B.40° C.25° D.20°
14.(2018·菏泽)如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA等于(D)
A.64° B.58° C.32° D.26°
15.如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正弦值等于.
16.如图所示,在⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为50°.
17.(教材P52练习T3变式)如图,在⊙O中,A,B是圆上的两点,已知∠AOB=40°,直径CD∥AB,连接AC,则∠BAC=35°.
18.如图,点A,B,C三点在⊙O上,过C作CD∥AB与⊙O相交于D点,E是上一点,且满足AD=DE,连接BD与AE相交于点F.求证:△AFD∽△ABC.
证明:∵AB∥CD,
∴∠BAC=∠ACD.
∵AD=DE,∴=.
∴∠DAE=∠AED.
∴∠DAE=∠AED=∠ACD=∠BAC.
∵∠ADF=∠ACB,∠DAE=∠BAC,
∴△AFD∽△ABC.
综合题
19.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状,并证明你的结论;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论.
证明:(1)△ABC是等边三角形.
在⊙O中,
∵∠BAC与∠CPB是所对的圆周角,
∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC.
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°.
∴△ABC为等边三角形.
(2)在PC上截取PD=AP,连接AD,
∵∠APC=60°,
∴△APD是等边三角形.
∴AD=AP=PD,∠ADP=60°,
即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB.
在△APB和△ADC中,
∴△APB≌△ADC(AAS).
∴BP=CD.
又∵PD=AP.
∴CP=CD+PD=BP+AP.
第2课时 圆周角定理推论2及圆内接四边形的性质
基础题
知识点1 圆周角定理推论2
1.(2017·福建)如图,AB是⊙O的直径,C,D是⊙O上位于AB异侧的两点.则下列四个角中,一定与∠ACD互余的角是(D)
A.∠ADC B.∠ABD
C.∠BAC D.∠BAD
2.如图,小华同学设计了一个量直径的测量器,标有刻度的尺子OA,OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位长度,OF=6个单位长度,则圆的直径为(B)
A.12个单位长度 B.10个单位长度
C.4个单位长度 D.15个单位长度
3.如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为(C)
A.20° B.40° C.50° D.70°
4.如图,CD是⊙O的直径,已知∠1=30°,则∠2=(C)
A.30° B.45° C.60° D.70°
5.如图,把直角三角形的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M,N,量得OM=8 cm,ON=6 cm,则该圆玻璃镜的半径是(B)
A. cm
B.5 cm
C.6 cm
D.10 cm
6.如图,AB是⊙O的直径,点D在⊙O上,∠AOD=130°,BC∥OD交⊙O于C,求∠A的度数.
解:∵∠AOD=130°,
∴∠BOD=50°.
∵BC∥OD,∴∠B=∠BOD=50°.
∵AB是⊙O的直径,
∴∠ACB=90°.
∴∠A=90°-∠B=40°.
知识点2 圆内接四边形对角互补
7.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点.若∠BAD=105°,则∠DCE的大小是(B)
A.115° B.105° C.100° D.95°
8.(教材P55例4变式)(2018·邵阳)如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是(B)
A.80° B.120° C.100° D.90°
9.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD=110°,则∠BAD=70°.
10.如图,已知∠EAD是圆内接四边形ABCD的一个外角,并且BD=DC.求证:AD平分∠EAC.
证明:∵∠EAD+∠BAD=180°,∠DCB+∠BAD=180°,
∴∠EAD=∠DCB.
∵BD=DC,∴∠DBC=∠DCB.
又∵∠DBC=∠DAC,
∴∠EAD=∠DAC,即AD平分∠EAC.
易错点 对圆内接四边形的概念理解不清导致错误
11.如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=110°,则∠α=140°.
中档题
12.在圆内接四边形ABCD中,若∠A∶∠B∶∠C=1∶2∶5,则∠D等于(B)
A.60° B.120° C.140° D.150°
13.如图,AB为⊙O的直径,关于角p,q,r,s之间的关系:①p=2q;②q=r;③p+s=180°中,正确的是(A)
A.只有①和② B.只有①和③
C.只有②和③ D.①②③
14.(2018·白银)如图,⊙A过点O(0,0),C(,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是(B)
A.15° B.30° C.45° D.60°
15.(2018·北京)如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB=70°.
16.如图,已知点A,B,C,D均在⊙O上,CD为∠ACE的平分线.
(1)求证:△ABD为等腰三角形;
(2)若∠DCE=45°,BD=6,求⊙O的半径.
解:(1)证明:
∵CD平分∠ECA,
∴∠ECD=∠DCA.
∵∠ECD+∠DCB=180°,∠DCB+∠BAD=180°,
∴∠ECD=∠DAB.
又∵∠DCA=∠DBA,
∴∠DBA=∠DAB.
∴DB=DA.
∴△ABD是等腰三角形.
(2)∵∠DCE=∠DCA=45°,
∴∠ECA=∠ACB=90°.
∴∠BDA=90°.∴AB是直径.
∵BD=AD=6,
∴AB===6.
∴⊙O的半径为3.
17.(2018·宜昌)如图,在△ABC中,AB=AC.以AB为直径的半圆交AC于点D,交BC于点E.延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.
解:(1)证明:∵AB为半圆的直径,
∴∠AEB=90°,
∵AB=AC,
∴CE=BE.
又∵EF=AE,
∴四边形ABFC是平行四边形.
又∵AB=AC,(或∠AEB=90°)
∴平行四边形ABFC是菱形.
(2)连接BD.
∵AD=7,BE=CE=2,
设CD=x,则AB=AC=7+x.
∵AB为半圆的直径,
∴∠ADB=90°.
∴AB2-AD2=CB2-CD2.
∴(7+x)2-72=42-x2.
∴x1=1或x2=-8(舍去).
∴S半圆=×π×42=8π.
∴BD=.
∴S菱形ABFC=8.
综合题
18.如图,在⊙O中,直径AB的两侧有定点C和动点P,点P在上运动(不与A,B重合),过点C作CP的垂线,与PB的延长线交于点Q.
(1)试猜想:△PCQ与△ACB具有何种关系?(不要求证明)
(2)当点P运动到什么位置时,△ABC≌△PCB?并给出证明.
解:(1)△PCQ∽△ACB.
(2)当为半圆时,
△ABC≌△PCB.
证明:∵AB是直径,
∴∠ACB=90°.
∵为半圆,
∴CP是直径.
∴∠PBC=90°,AB=CP.
∵CB是公共边,∴Rt△ABC≌Rt△PCB(HL).
