第二章2.6弧长与扇形面积练习试卷
图片预览




文档简介
2.6 弧长与扇形面积
第1课时 弧长
基础题
知识点 弧长公式(l=)及其应用
1.已知扇形的圆心角为60°,半径为1,则扇形的弧长为(D)
A. B.π C. D.
2.已知一弧的半径为3,弧长为2π,则此弧所对的圆心角为(C)
A.300° B.240° C.120° D.60°
3.圆心角为120°,弧长为12π的扇形半径为(C)
A.6 B.9 C.18 D.36
4.(2018·黄石)如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO=4,则的长为(D)
A.π B.π C.2π D.π
5.(教材P78例2变式)如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得到△A′B′C,则点B转过的路径长为(B)
A. B. C.π D.Π
6.如图所示,小亮坐在秋千上,秋千的绳长OA为2米,秋千绕点O旋转了60°,点A旋转到点A′,则的长为米.(结果保留π)
7.如图,已知正方形的边长为2 cm,以对角的两个顶点为圆心,2 cm长为半径画弧,则所得到的两条弧长度之和为2π__cm.(结果保留π)
8.如图,网格图中每个小正方形的边长为1,则的长l=π.
9.如图,一根绳子与半径为30 cm的滑轮的接触部分是,绳子AC和BD所在的直线成30°角.请你测算一下接触部分的长.(结果保留π)
解:连接OC,OD,则OC⊥AC,BD⊥OD.
又∵AC与BD的夹角为30°,
∴∠COD=150°.
∴的长为=25π(cm).
易错点 忽视题中条件
10.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25 cm,贴纸部分的宽BD为15 cm.若纸扇两面贴纸,则贴纸的面积为350πcm2.
中档题
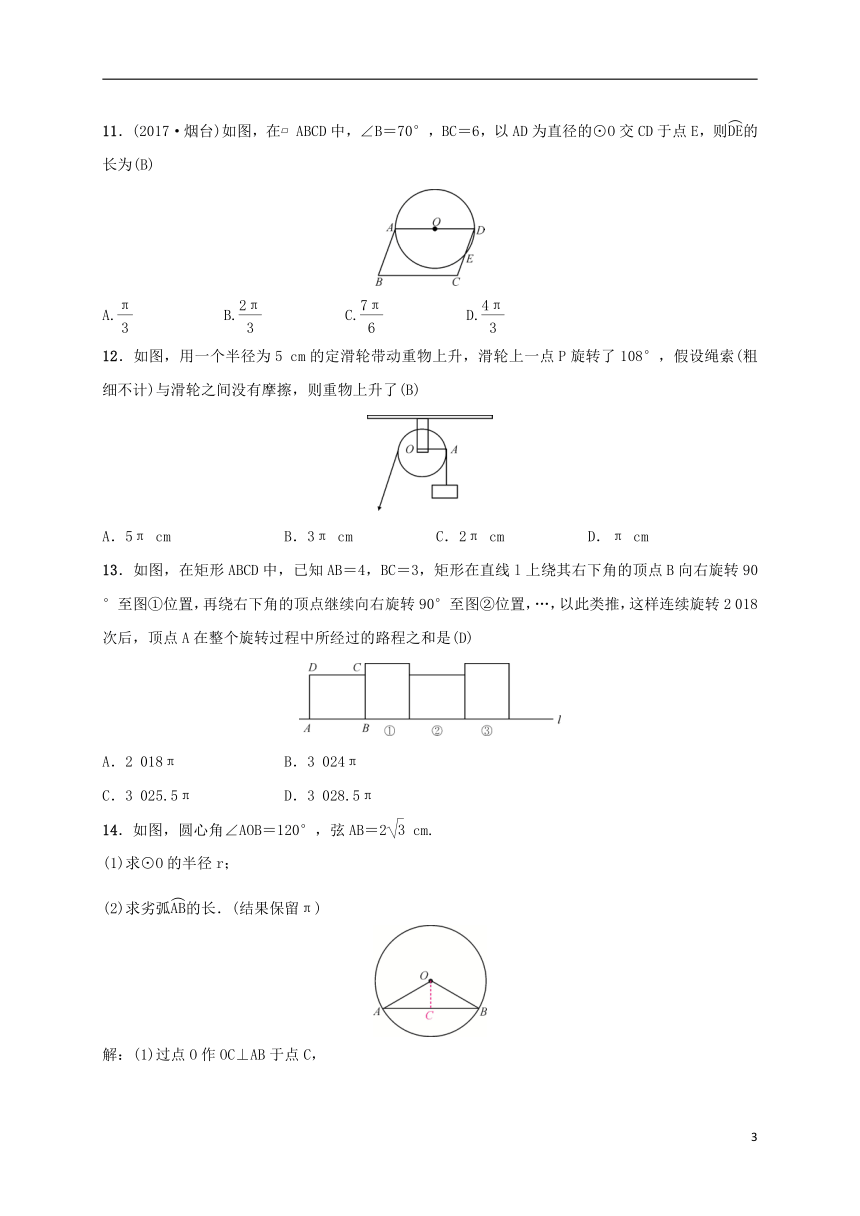
11.(2017·烟台)如图,在?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则的长为(B)
A. B. C. D.
12.如图,用一个半径为5 cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了(B)
A.5π cm B.3π cm C.2π cm D.π cm
13.如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2 018次后,顶点A在整个旋转过程中所经过的路程之和是(D)
A.2 018π B.3 024π
C.3 025.5π D.3 028.5π
14.如图,圆心角∠AOB=120°,弦AB=2 cm.
(1)求⊙O的半径r;
(2)求劣弧的长.(结果保留π)
解:(1)过点O作OC⊥AB于点C,
则AC=AB= cm.
∵∠AOB=120°,OA=OB,
∴∠A=30°.
∴在Rt△AOC中,
r=OA==2 cm.
(2)劣弧的长为= cm.
15.图1,2,…,m分别是边长均大于2的三角形,四边形,…,凸n边形,分别以它们的各顶点为圆心,以1为半径画弧与两邻边相交,得到3条弧,4条弧,…,n条弧.
(1)图1中3条弧的弧长的和为π,图2中4条弧的弧长的和为2π;
(2)求图m中n条弧的弧长的和.(用n表示)
解:(n-2)π.
综合题
16.某商场为了迎接“六一”儿童节的到来,制造了一个超大的“不倒翁”.小灵对“不倒翁”很感兴趣,原来“不倒翁”的底部是由一个空心的半球做成的,并在底部的中心(即图中的C处)固定一个重物,再从正中心立起一根杆子,在杆子上做些装饰,在重力和杠杆的作用下,“不倒翁”就会左摇右晃,又不会完全倒下去.小灵画出剖面图,进行细致研究:圆弧的圆心为点O,过点O的木杆CD长为260 cm,OA,OB为圆弧的半径,长为90 cm(作为木杆的支架),且OA,OB关于CD对称,的长为30π cm.当木杆CD向右摆动使点B落在地面上(即圆弧与直线l相切于点B)时,木杆的顶端点D到直线l的距离DF是多少厘米?
解:∵的长为30π cm,OA,OB为圆弧的半径,长为90 cm,
根据弧长公式l=,得30π=,
解得n=60°.
即∠AOB=60°,从而∠BOE=∠COA=30°.
∵OB=90 cm,∴OE=60 cm.
∴DE=(170+60)cm.
∴DF=(90+85 )cm.
第2课时 扇形的面积
基础题
知识点1 扇形的面积
1.已知扇形的半径为6 cm,圆心角为120°,则这个扇形的面积是(B)
A.36π cm2 B.12π cm2
C.9π cm2 D.6π cm2
2.如果扇形的圆心角为150°,它的面积为240π cm2,那么扇形的半径为(B)
A.48 cm B.24 cm
C.12 cm D.6 cm
3.若一个扇形的面积是12π,它的弧长是4π,则它的半径是(D)
A.3 B.4 C.5 D.6
4.圆心角是60°且半径为2的扇形面积为π.(结果保留π)
5.已知扇形的圆心角为150°,它所对应的弧长为20π cm,则此扇形的半径是24cm,面积是240πcm2.(结果保留π)
6.如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是.
7.(2018·巴中)如图所示,以六边形的每个顶点为圆心,1为半径画圆,则图中阴影部分的面积为2π.
知识点2 与扇形有关的阴影部分的面积
8.如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是(A)
A.- B.-2 C.- D.-
9.(2017·湘潭)如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为E,∠AOB=90°,则阴影部分的面积是(D)
A.4π-4 B.2π-4 C.4π D.2π
10.(2018·重庆A卷)如图,在矩形ABCD中,AB=3,AD=2,以点A为圆心,AD长为半径画弧,交AB于点E,图中阴影部分的面积是6-π.(结果保留π)
11.如图,PA,PB分别与⊙O相切于点A,B,∠APB=60°,连接AO,BO.
(1)所对的圆心角∠AOB=120°;
(2)若OA=3,求阴影部分的面积.
解:连接OP,
则∠OPA=∠OPB=∠APB=30°.
在Rt△OAP中,OA=3,∴AP=3.
∴S△OPA=×3×3=.
∴S阴影=2×-=9-3π.
中档题
12.(2018·德州)如图,从一块直径为2 m的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为(A)
A. m2 B.π m2 C.π m2 D.2π m2
13.如图,CD是半圆O的直径,弦AB∥CD,且CD=6,∠ADB=30°,则阴影部分的面积是(B)
A.π B.π C.3π D.6π
14.如图,在平面直角坐标系中,点A的坐标(-2,0),△ABO是直角三角形,∠AOB=60°.现将Rt△ABO绕原点O按顺时针方向旋转到Rt△A′B′O的位置,则此时边OB扫过的面积为π.
15.(2017·郴州)如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3.
(1)求证:AB平分∠OAD;
(2)若点E是优弧上一点,且∠AEB=60°,求扇形OAB的面积.(计算结果保留π)
解:(1)证明:连接OB,
∵BC切⊙O于点B,
∴OB⊥BC.
∵AD⊥BC,
∴AD∥OB.
∴∠DAB=∠OBA.
∵OA=OB,
∴∠OAB=∠OBA.
∴∠DAB=∠OAB.
∴AB平分∠OAD.
(2)∵点E是优弧上一点,且∠AEB=60°,
∴∠AOB=2∠AEB=120°,
∴扇形OAB的面积为=3π.
16.如图,线段AB与⊙O相切于点C,连接OA,OB,OB交⊙O于点D,已知OA=OB=6,AB=6.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
解:(1)连接OC,则OC⊥AB.∵OA=OB,
∴AC=BC=AB=×6=3.
在Rt△AOC中,OC==3,
∴⊙O的半径为3.
(2)∵OC=OB,∴∠B=30°,∠COD=60°.
∴S扇形OCD==π.
∴S阴影=SRt△OBC-S扇形OCD=OC·CB-π=-.
综合题
17.如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC,BD.
(1)求证:AC=BD;
(2)若图中阴影部分的面积是π cm2,OA=2 cm,求OC的长.
解:(1)证明:∵∠AOB=∠COD=90°,
∴∠AOC+∠AOD=∠BOD+∠AOD.
∴∠AOC=∠BOD.
∵AO=BO,CO=DO,
∴△AOC≌△BOD(SAS).
∴AC=BD.
(2)根据题意,得
S阴影=-=,
∴π=,解得OC=1.
∴OC=1cm.
第1课时 弧长
基础题
知识点 弧长公式(l=)及其应用
1.已知扇形的圆心角为60°,半径为1,则扇形的弧长为(D)
A. B.π C. D.
2.已知一弧的半径为3,弧长为2π,则此弧所对的圆心角为(C)
A.300° B.240° C.120° D.60°
3.圆心角为120°,弧长为12π的扇形半径为(C)
A.6 B.9 C.18 D.36
4.(2018·黄石)如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO=4,则的长为(D)
A.π B.π C.2π D.π
5.(教材P78例2变式)如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得到△A′B′C,则点B转过的路径长为(B)
A. B. C.π D.Π
6.如图所示,小亮坐在秋千上,秋千的绳长OA为2米,秋千绕点O旋转了60°,点A旋转到点A′,则的长为米.(结果保留π)
7.如图,已知正方形的边长为2 cm,以对角的两个顶点为圆心,2 cm长为半径画弧,则所得到的两条弧长度之和为2π__cm.(结果保留π)
8.如图,网格图中每个小正方形的边长为1,则的长l=π.
9.如图,一根绳子与半径为30 cm的滑轮的接触部分是,绳子AC和BD所在的直线成30°角.请你测算一下接触部分的长.(结果保留π)
解:连接OC,OD,则OC⊥AC,BD⊥OD.
又∵AC与BD的夹角为30°,
∴∠COD=150°.
∴的长为=25π(cm).
易错点 忽视题中条件
10.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25 cm,贴纸部分的宽BD为15 cm.若纸扇两面贴纸,则贴纸的面积为350πcm2.
中档题
11.(2017·烟台)如图,在?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则的长为(B)
A. B. C. D.
12.如图,用一个半径为5 cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了(B)
A.5π cm B.3π cm C.2π cm D.π cm
13.如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2 018次后,顶点A在整个旋转过程中所经过的路程之和是(D)
A.2 018π B.3 024π
C.3 025.5π D.3 028.5π
14.如图,圆心角∠AOB=120°,弦AB=2 cm.
(1)求⊙O的半径r;
(2)求劣弧的长.(结果保留π)
解:(1)过点O作OC⊥AB于点C,
则AC=AB= cm.
∵∠AOB=120°,OA=OB,
∴∠A=30°.
∴在Rt△AOC中,
r=OA==2 cm.
(2)劣弧的长为= cm.
15.图1,2,…,m分别是边长均大于2的三角形,四边形,…,凸n边形,分别以它们的各顶点为圆心,以1为半径画弧与两邻边相交,得到3条弧,4条弧,…,n条弧.
(1)图1中3条弧的弧长的和为π,图2中4条弧的弧长的和为2π;
(2)求图m中n条弧的弧长的和.(用n表示)
解:(n-2)π.
综合题
16.某商场为了迎接“六一”儿童节的到来,制造了一个超大的“不倒翁”.小灵对“不倒翁”很感兴趣,原来“不倒翁”的底部是由一个空心的半球做成的,并在底部的中心(即图中的C处)固定一个重物,再从正中心立起一根杆子,在杆子上做些装饰,在重力和杠杆的作用下,“不倒翁”就会左摇右晃,又不会完全倒下去.小灵画出剖面图,进行细致研究:圆弧的圆心为点O,过点O的木杆CD长为260 cm,OA,OB为圆弧的半径,长为90 cm(作为木杆的支架),且OA,OB关于CD对称,的长为30π cm.当木杆CD向右摆动使点B落在地面上(即圆弧与直线l相切于点B)时,木杆的顶端点D到直线l的距离DF是多少厘米?
解:∵的长为30π cm,OA,OB为圆弧的半径,长为90 cm,
根据弧长公式l=,得30π=,
解得n=60°.
即∠AOB=60°,从而∠BOE=∠COA=30°.
∵OB=90 cm,∴OE=60 cm.
∴DE=(170+60)cm.
∴DF=(90+85 )cm.
第2课时 扇形的面积
基础题
知识点1 扇形的面积
1.已知扇形的半径为6 cm,圆心角为120°,则这个扇形的面积是(B)
A.36π cm2 B.12π cm2
C.9π cm2 D.6π cm2
2.如果扇形的圆心角为150°,它的面积为240π cm2,那么扇形的半径为(B)
A.48 cm B.24 cm
C.12 cm D.6 cm
3.若一个扇形的面积是12π,它的弧长是4π,则它的半径是(D)
A.3 B.4 C.5 D.6
4.圆心角是60°且半径为2的扇形面积为π.(结果保留π)
5.已知扇形的圆心角为150°,它所对应的弧长为20π cm,则此扇形的半径是24cm,面积是240πcm2.(结果保留π)
6.如图所示,在3×3的方格纸中,每个小方格都是边长为1的正方形,点O,A,B均为格点,则扇形OAB的面积大小是.
7.(2018·巴中)如图所示,以六边形的每个顶点为圆心,1为半径画圆,则图中阴影部分的面积为2π.
知识点2 与扇形有关的阴影部分的面积
8.如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是(A)
A.- B.-2 C.- D.-
9.(2017·湘潭)如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为E,∠AOB=90°,则阴影部分的面积是(D)
A.4π-4 B.2π-4 C.4π D.2π
10.(2018·重庆A卷)如图,在矩形ABCD中,AB=3,AD=2,以点A为圆心,AD长为半径画弧,交AB于点E,图中阴影部分的面积是6-π.(结果保留π)
11.如图,PA,PB分别与⊙O相切于点A,B,∠APB=60°,连接AO,BO.
(1)所对的圆心角∠AOB=120°;
(2)若OA=3,求阴影部分的面积.
解:连接OP,
则∠OPA=∠OPB=∠APB=30°.
在Rt△OAP中,OA=3,∴AP=3.
∴S△OPA=×3×3=.
∴S阴影=2×-=9-3π.
中档题
12.(2018·德州)如图,从一块直径为2 m的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为(A)
A. m2 B.π m2 C.π m2 D.2π m2
13.如图,CD是半圆O的直径,弦AB∥CD,且CD=6,∠ADB=30°,则阴影部分的面积是(B)
A.π B.π C.3π D.6π
14.如图,在平面直角坐标系中,点A的坐标(-2,0),△ABO是直角三角形,∠AOB=60°.现将Rt△ABO绕原点O按顺时针方向旋转到Rt△A′B′O的位置,则此时边OB扫过的面积为π.
15.(2017·郴州)如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3.
(1)求证:AB平分∠OAD;
(2)若点E是优弧上一点,且∠AEB=60°,求扇形OAB的面积.(计算结果保留π)
解:(1)证明:连接OB,
∵BC切⊙O于点B,
∴OB⊥BC.
∵AD⊥BC,
∴AD∥OB.
∴∠DAB=∠OBA.
∵OA=OB,
∴∠OAB=∠OBA.
∴∠DAB=∠OAB.
∴AB平分∠OAD.
(2)∵点E是优弧上一点,且∠AEB=60°,
∴∠AOB=2∠AEB=120°,
∴扇形OAB的面积为=3π.
16.如图,线段AB与⊙O相切于点C,连接OA,OB,OB交⊙O于点D,已知OA=OB=6,AB=6.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
解:(1)连接OC,则OC⊥AB.∵OA=OB,
∴AC=BC=AB=×6=3.
在Rt△AOC中,OC==3,
∴⊙O的半径为3.
(2)∵OC=OB,∴∠B=30°,∠COD=60°.
∴S扇形OCD==π.
∴S阴影=SRt△OBC-S扇形OCD=OC·CB-π=-.
综合题
17.如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC,BD.
(1)求证:AC=BD;
(2)若图中阴影部分的面积是π cm2,OA=2 cm,求OC的长.
解:(1)证明:∵∠AOB=∠COD=90°,
∴∠AOC+∠AOD=∠BOD+∠AOD.
∴∠AOC=∠BOD.
∵AO=BO,CO=DO,
∴△AOC≌△BOD(SAS).
∴AC=BD.
(2)根据题意,得
S阴影=-=,
∴π=,解得OC=1.
∴OC=1cm.
