人教版九年级上数学24.3正多边形和圆 练习题(含答案)
文档属性
| 名称 | 人教版九年级上数学24.3正多边形和圆 练习题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 157.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-29 00:00:00 | ||
图片预览

文档简介
24.3 正多边形和圆
01 基础题
知识点1 认识正多边形
1.下面图形中,是正多边形的是(C)
A.矩形 B.菱形
C.正方形 D.等腰梯形
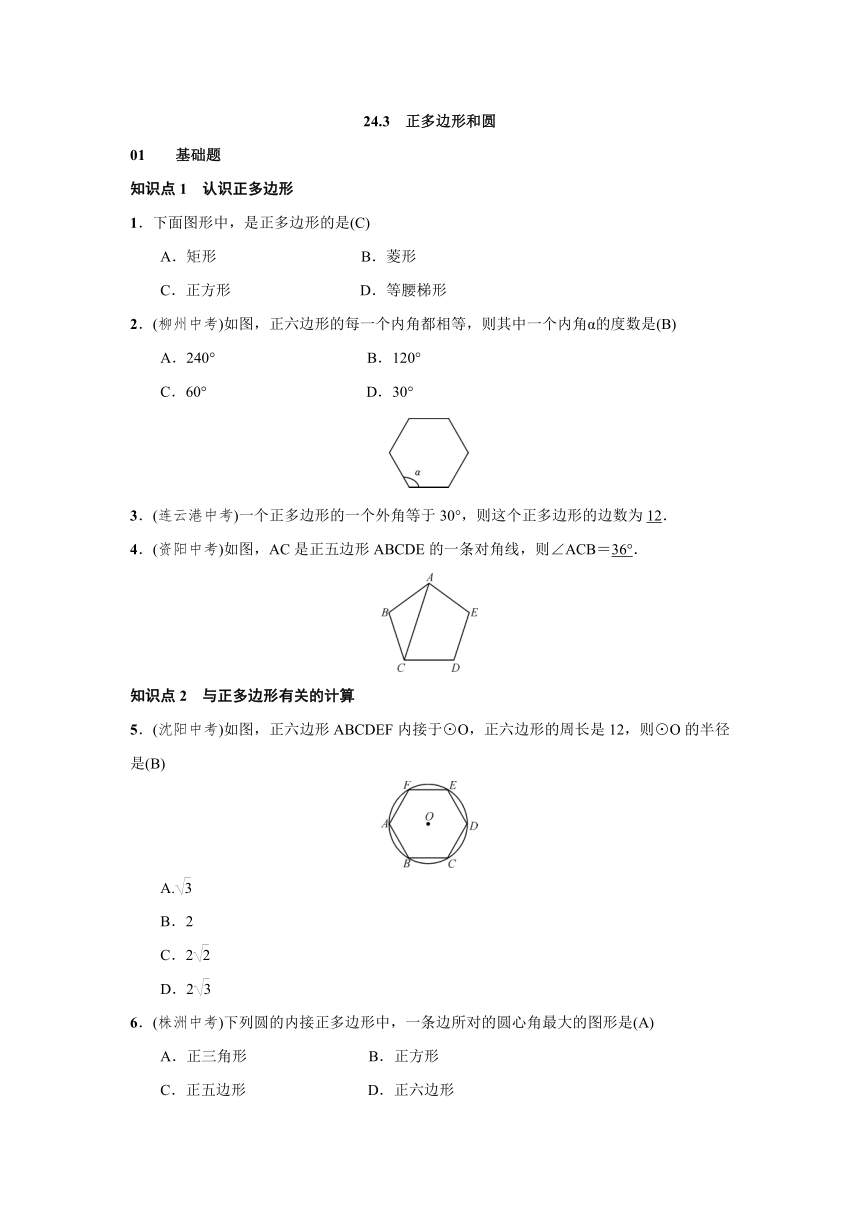
2.(柳州中考)如图,正六边形的每一个内角都相等,则其中一个内角α的度数是(B)
A.240° B.120°
C.60° D.30°
3.(连云港中考)一个正多边形的一个外角等于30°,则这个正多边形的边数为12.
4.(资阳中考)如图,AC是正五边形ABCDE的一条对角线,则∠ACB=36°.
知识点2 与正多边形有关的计算
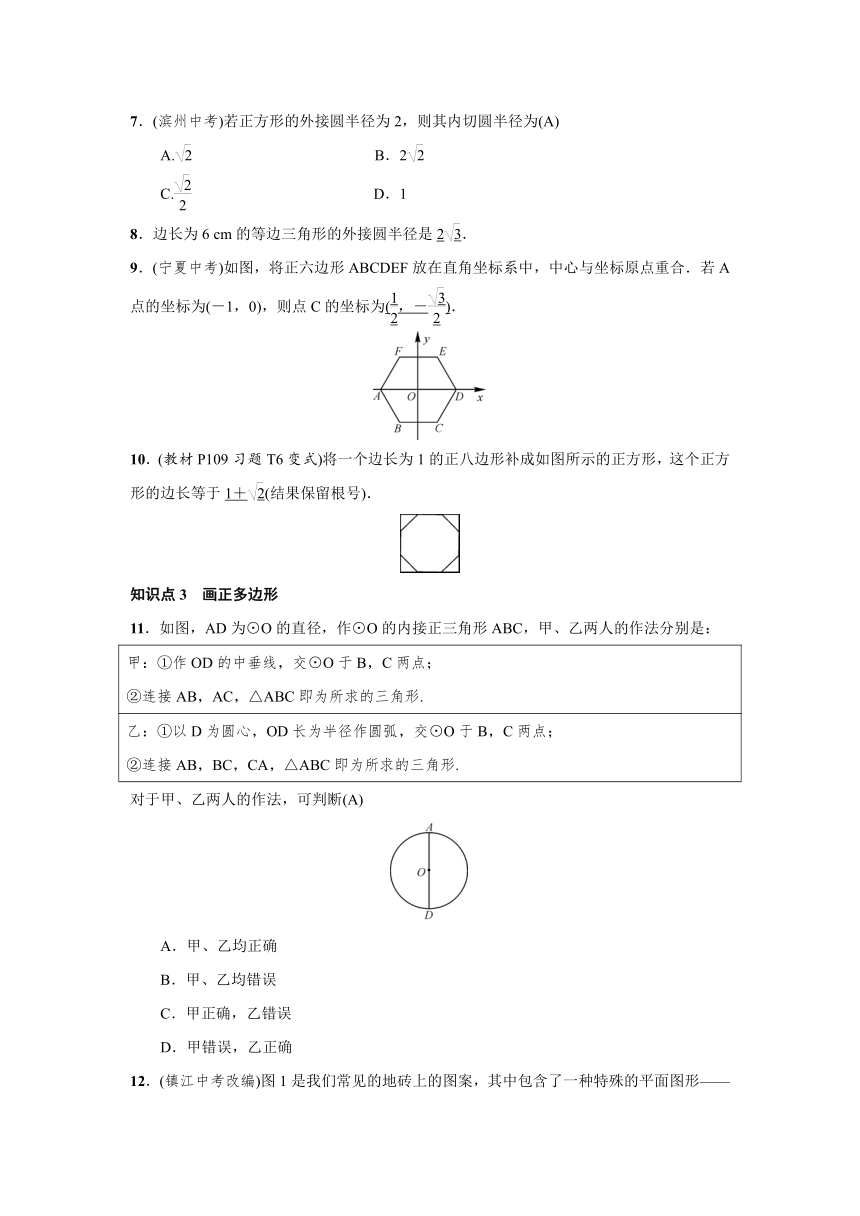
5.(沈阳中考)如图,正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是(B)
A.
B.2
C.2
D.2
6.(株洲中考)下列圆的内接正多边形中,一条边所对的圆心角最大的图形是(A)
A.正三角形 B.正方形
C.正五边形 D.正六边形
7.(滨州中考)若正方形的外接圆半径为2,则其内切圆半径为(A)
A. B.2
C. D.1
8.边长为6 cm的等边三角形的外接圆半径是2.
9.(宁夏中考)如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合.若A点的坐标为(-1,0),则点C的坐标为(,-).
10.(教材P109习题T6变式)将一个边长为1的正八边形补成如图所示的正方形,这个正方形的边长等于1+(结果保留根号).
知识点3 画正多边形
11.如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别是:
甲:①作OD的中垂线,交⊙O于B,C两点;
②连接AB,AC,△ABC即为所求的三角形.
乙:①以D为圆心,OD长为半径作圆弧,交⊙O于B,C两点;
②连接AB,BC,CA,△ABC即为所求的三角形.
对于甲、乙两人的作法,可判断(A)
A.甲、乙均正确
B.甲、乙均错误
C.甲正确,乙错误
D.甲错误,乙正确
12.(镇江中考改编)图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.
如图2,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).
解:如图.
02 中档题
13.正三角形内切圆半径r与外接圆半径R之间的关系为(D)
A.4R=5r B.3R=4r
C.2R=3r D.R=2r
14.(滨州中考)如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是(C)
A.(2,-3) B.(2,3)
C.(3,2) D.(3,-2)
15.(达州中考)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是(A)
A. B. C. D.
16.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为(A)
A.2a2 B.3a2 C.4a2 D.5a2
17.(山西中考命题专家原创)如图,圆O与正八边形OABCDEFG的边OA,OG分别交于点M,N,则弧MN所对的圆心角∠MPN的大小为67.5°.
18.(连云港中考)如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10=75°.
19.如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.
(1)正方形ABCD与正六边形AEFCGH的边长之比为∶1;
(2)连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.
解:BE是⊙O的内接正十二边形的一边,
理由:连接OA,OB,OE,
在正方形ABCD中,
∠AOB=90°,
在正六边形AEFCGH中,∠AOE=60°,
∴∠BOE=30°.
∵n==12,
∴BE是正十二边形的边.
03 综合题
20.如图1,2,3,…,m,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…正n边形ABCDEF…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是90°,图3中∠MON的度数是72°;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
解:(1)连接OA,OB.
∵正三角形ABC内接于⊙O,
∴OA=OB,∠OAM=∠OBA=30°,
∠AOB=120°.
∵BM=CN,AB=BC,
∴AM=BN.
∴△AOM≌△BON(SAS).
∴∠AOM=∠BON.
∴∠AOM+∠BOM=∠BON+∠BOM,
即∠AOB=∠MON.
∴∠MON=120°.
(3)∠MON=.
01 基础题
知识点1 认识正多边形
1.下面图形中,是正多边形的是(C)
A.矩形 B.菱形
C.正方形 D.等腰梯形
2.(柳州中考)如图,正六边形的每一个内角都相等,则其中一个内角α的度数是(B)
A.240° B.120°
C.60° D.30°
3.(连云港中考)一个正多边形的一个外角等于30°,则这个正多边形的边数为12.
4.(资阳中考)如图,AC是正五边形ABCDE的一条对角线,则∠ACB=36°.
知识点2 与正多边形有关的计算
5.(沈阳中考)如图,正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是(B)
A.
B.2
C.2
D.2
6.(株洲中考)下列圆的内接正多边形中,一条边所对的圆心角最大的图形是(A)
A.正三角形 B.正方形
C.正五边形 D.正六边形
7.(滨州中考)若正方形的外接圆半径为2,则其内切圆半径为(A)
A. B.2
C. D.1
8.边长为6 cm的等边三角形的外接圆半径是2.
9.(宁夏中考)如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合.若A点的坐标为(-1,0),则点C的坐标为(,-).
10.(教材P109习题T6变式)将一个边长为1的正八边形补成如图所示的正方形,这个正方形的边长等于1+(结果保留根号).
知识点3 画正多边形
11.如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别是:
甲:①作OD的中垂线,交⊙O于B,C两点;
②连接AB,AC,△ABC即为所求的三角形.
乙:①以D为圆心,OD长为半径作圆弧,交⊙O于B,C两点;
②连接AB,BC,CA,△ABC即为所求的三角形.
对于甲、乙两人的作法,可判断(A)
A.甲、乙均正确
B.甲、乙均错误
C.甲正确,乙错误
D.甲错误,乙正确
12.(镇江中考改编)图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.
如图2,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).
解:如图.
02 中档题
13.正三角形内切圆半径r与外接圆半径R之间的关系为(D)
A.4R=5r B.3R=4r
C.2R=3r D.R=2r
14.(滨州中考)如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是(C)
A.(2,-3) B.(2,3)
C.(3,2) D.(3,-2)
15.(达州中考)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是(A)
A. B. C. D.
16.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为(A)
A.2a2 B.3a2 C.4a2 D.5a2
17.(山西中考命题专家原创)如图,圆O与正八边形OABCDEFG的边OA,OG分别交于点M,N,则弧MN所对的圆心角∠MPN的大小为67.5°.
18.(连云港中考)如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10=75°.
19.如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.
(1)正方形ABCD与正六边形AEFCGH的边长之比为∶1;
(2)连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.
解:BE是⊙O的内接正十二边形的一边,
理由:连接OA,OB,OE,
在正方形ABCD中,
∠AOB=90°,
在正六边形AEFCGH中,∠AOE=60°,
∴∠BOE=30°.
∵n==12,
∴BE是正十二边形的边.
03 综合题
20.如图1,2,3,…,m,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…正n边形ABCDEF…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图1中∠MON的度数;
(2)图2中∠MON的度数是90°,图3中∠MON的度数是72°;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
解:(1)连接OA,OB.
∵正三角形ABC内接于⊙O,
∴OA=OB,∠OAM=∠OBA=30°,
∠AOB=120°.
∵BM=CN,AB=BC,
∴AM=BN.
∴△AOM≌△BON(SAS).
∴∠AOM=∠BON.
∴∠AOM+∠BOM=∠BON+∠BOM,
即∠AOB=∠MON.
∴∠MON=120°.
(3)∠MON=.
同课章节目录
