数学五年级上人教版5等式的性质 课件(共22张PPT)
文档属性
| 名称 | 数学五年级上人教版5等式的性质 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 110.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-01 07:28:23 | ||
图片预览






文档简介
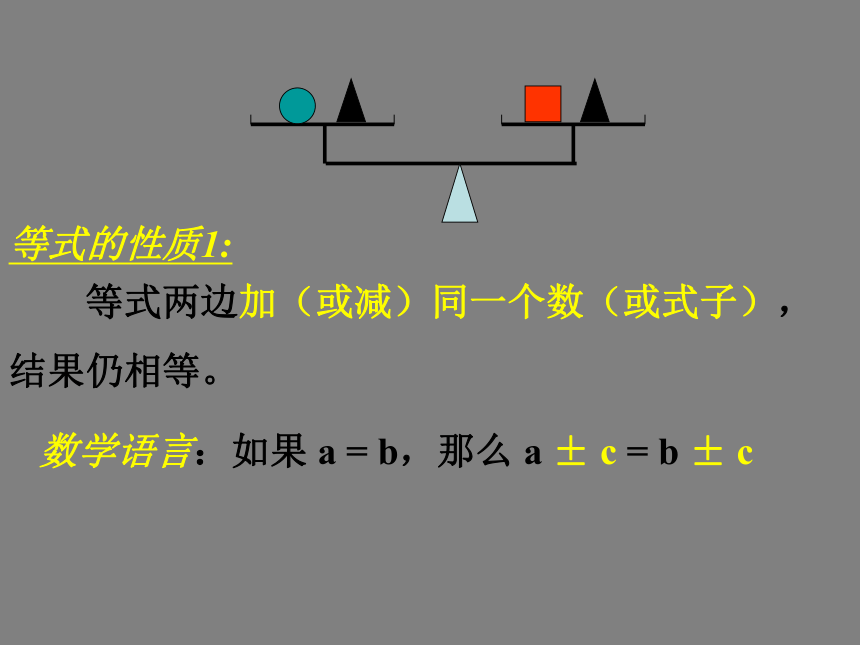
课件22张PPT。等式的性质等式的性质1: 等式两边加(或减)同一个数(或式子),
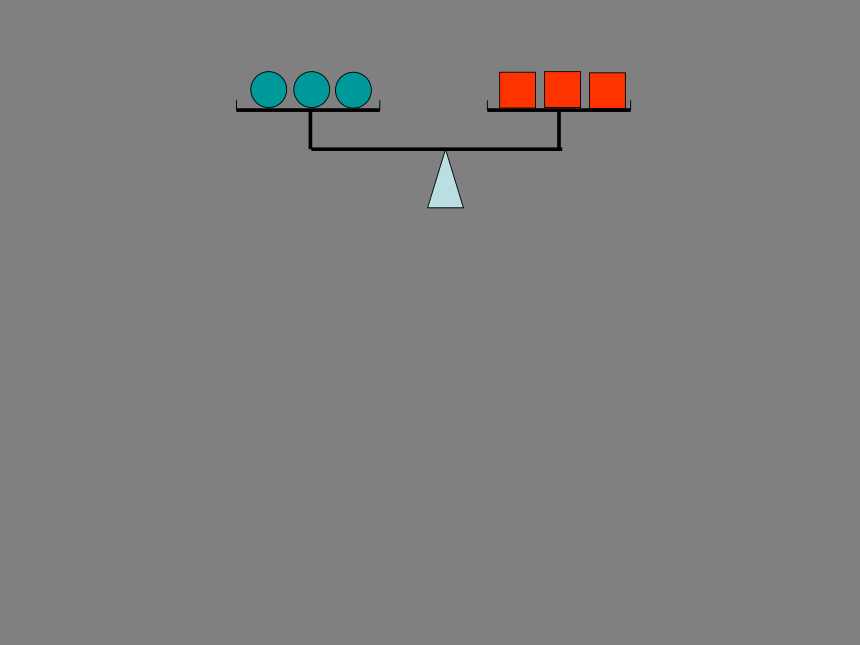
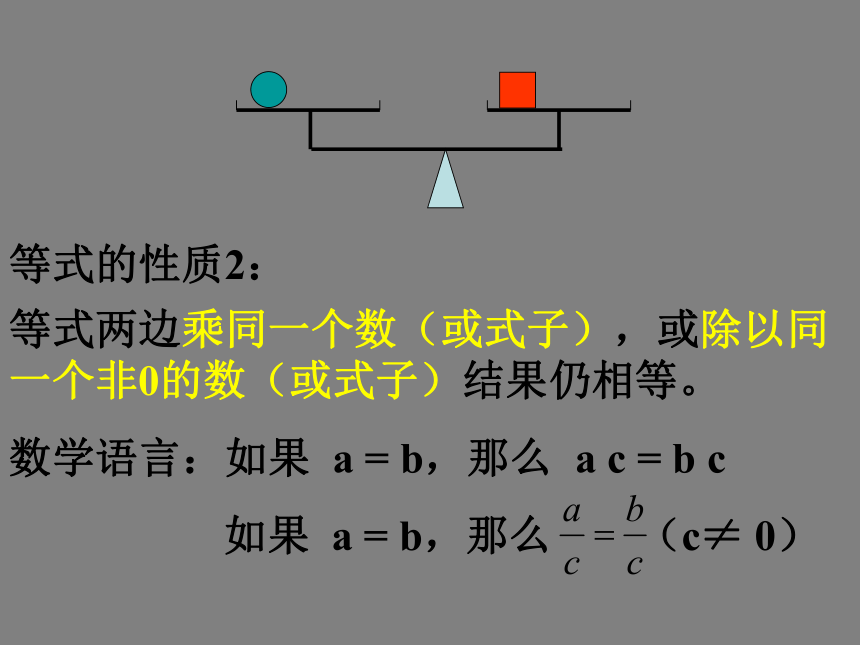
结果仍相等。数学语言:如果 a = b,那么 a ± c = b ± c等式的性质1等式的性质1等式的性质2等式的性质2-y-1随堂练习:
1.填空并说出是根据等式的哪条性质及怎样变形(改变式子的形式)
(1)如果3x+7=8,那么
3x=8-______.随堂练习:
1.填空并说出是根据性质及怎
样变形(改变式子的形式)
(1)如果3x+7=8那么 3x=8-_7_;
答:根据等式的性质1,两边 都减去7。(2)如果2x=5-3x, 那么 2x+__=5;
随堂练习:
1.填空并说出是根条性质及怎
样变形(改变式子的形式)
(2)如果2x=5-3x, 那么2x+3x=5;
答:根据性质1,两边都加3x.(3)如果2x=10,那么x=____;
随堂练习:
1.填空并说出是根据等性质及怎
样变形(改变式子的形式)
(3)如果2x=10,那么x=__5__;
答:根据等式的性质2,两 边同时除以2。(4)如果 0.2x=5 那么x=_.随堂练习:
1.填空并说出是根条性质及怎
样变形(改变式子的形式)
(4)如果 0.2x=5, 那么x=_25_.
答:根据等式性质2,两 边都乘以5。
BDx = 0x = 9练习4. 已知:X=Y,a为任意有理数.(1),(2),(3),(4)成立,(5)不一定成立.例2 解下列方程:
(1)x+2=5;(2) 3=x-5解:(1)方程两边同时减去2得 x+2-2=5-2
于是 x=3.例2 解下列方程:
(2) 3=x-5
(2)解:方程两边同时加上5,得 3+5=x-5+5于是 8=x.
习惯上,我们写为x=8.例3解下列方程:
(1)-3x=15; (2) -0.5n-2=10
解 (1)方程两边同时除以-3,
得化简,得 x=-5
例3解下列方程:
(2) -0.5n-2=10 (2)解: 方程两边同时加上2,得 - 0.5n -2+2=10+2 化简,得 - 0.5n =12方程两边同时乘-2,得 n=-24随堂练习:
5.利用等式的性质解下列方程:
(1)x-9=8; (2) x+2a=3a(a为已知常数)
(3) 3x+4=13; (4) 0.2x-1=5.解 (1)方程两边同时加上9,得x-9+9=8+9于是 x=17.
随堂练习:
5.利用等式的性质解下列方程:
(2) x+2a=3a(a为已知常数) (2)解:方程两边同时减去2a,得x+2a-2a=3a-2a
于是 x=a.
(3)方程两边同时减去4,有
(3) 3x+4=13; (4) 0.2x-1=5.3x=9方程两边同时再除以3,有
∴ x=3.
(4)解: 方程两边同时加上1,有 (4) 0.2x-1=5.0.2x-1+1=5+1于是 0.2x=6方程两边同时乘以5,有5 ×0.2x=5×6
于是 x=30.归纳总结2、解一元一次方程的实质就是利用等式的
性质求出未知数的值
结果仍相等。数学语言:如果 a = b,那么 a ± c = b ± c等式的性质1等式的性质1等式的性质2等式的性质2-y-1随堂练习:
1.填空并说出是根据等式的哪条性质及怎样变形(改变式子的形式)
(1)如果3x+7=8,那么
3x=8-______.随堂练习:
1.填空并说出是根据性质及怎
样变形(改变式子的形式)
(1)如果3x+7=8那么 3x=8-_7_;
答:根据等式的性质1,两边 都减去7。(2)如果2x=5-3x, 那么 2x+__=5;
随堂练习:
1.填空并说出是根条性质及怎
样变形(改变式子的形式)
(2)如果2x=5-3x, 那么2x+3x=5;
答:根据性质1,两边都加3x.(3)如果2x=10,那么x=____;
随堂练习:
1.填空并说出是根据等性质及怎
样变形(改变式子的形式)
(3)如果2x=10,那么x=__5__;
答:根据等式的性质2,两 边同时除以2。(4)如果 0.2x=5 那么x=_.随堂练习:
1.填空并说出是根条性质及怎
样变形(改变式子的形式)
(4)如果 0.2x=5, 那么x=_25_.
答:根据等式性质2,两 边都乘以5。
BDx = 0x = 9练习4. 已知:X=Y,a为任意有理数.(1),(2),(3),(4)成立,(5)不一定成立.例2 解下列方程:
(1)x+2=5;(2) 3=x-5解:(1)方程两边同时减去2得 x+2-2=5-2
于是 x=3.例2 解下列方程:
(2) 3=x-5
(2)解:方程两边同时加上5,得 3+5=x-5+5于是 8=x.
习惯上,我们写为x=8.例3解下列方程:
(1)-3x=15; (2) -0.5n-2=10
解 (1)方程两边同时除以-3,
得化简,得 x=-5
例3解下列方程:
(2) -0.5n-2=10 (2)解: 方程两边同时加上2,得 - 0.5n -2+2=10+2 化简,得 - 0.5n =12方程两边同时乘-2,得 n=-24随堂练习:
5.利用等式的性质解下列方程:
(1)x-9=8; (2) x+2a=3a(a为已知常数)
(3) 3x+4=13; (4) 0.2x-1=5.解 (1)方程两边同时加上9,得x-9+9=8+9于是 x=17.
随堂练习:
5.利用等式的性质解下列方程:
(2) x+2a=3a(a为已知常数) (2)解:方程两边同时减去2a,得x+2a-2a=3a-2a
于是 x=a.
(3)方程两边同时减去4,有
(3) 3x+4=13; (4) 0.2x-1=5.3x=9方程两边同时再除以3,有
∴ x=3.
(4)解: 方程两边同时加上1,有 (4) 0.2x-1=5.0.2x-1+1=5+1于是 0.2x=6方程两边同时乘以5,有5 ×0.2x=5×6
于是 x=30.归纳总结2、解一元一次方程的实质就是利用等式的
性质求出未知数的值
