2018年秋湘教版九年级数学上册《第1章反比例函数》测试题(解析版)
文档属性
| 名称 | 2018年秋湘教版九年级数学上册《第1章反比例函数》测试题(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 572.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-09-30 00:00:00 | ||
图片预览


文档简介
第1章 反比例函数
一、选择题(本大题共8小题,每小题4分,共32分)
1.下列函数表达式中,y不是x的反比例函数的是( )
A.y= B.y=
C.y= D.xy=
2.已知反比例函数y=的图象经过点(3,2),那么下列四个点中,也在这个函数图象上的是( )
A.(3,-2) B.(-2,-3)
C.(1,-6) D.(-6,1)
3.若双曲线y=经过第二、四象限,则k的取值范围是( )
A.k> B.k<
C.k= D.不存在
4.对于函数y=-,下列说法错误的是 ( )
A. 它的图象分布在第二、四象限
B. 它的图象既是轴对称图形又是中心对称图形
C. 当x>0时,y的值随x的增大而减小
D. 当x<0时,y的值随x的增大而增大
图1-Z-1
5.如图1-Z-1,市煤气公司计划在地下修建一个容积为104 m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是( )
图1-Z-2
6.已知(x1,y1),(x2,y2),(x3,y3)是反比例函数y=-的图象上的三个点,且x1<x2<0,x3>0,则y1,y2,y3的大小关系是( )
A.y3<y1<y2 B.y2<y1<y3
C.y1<y2<y3 D.y3<y2<y1
7.已知k1<0<k2,则函数y=和y=k2x-1的图象大致是( )
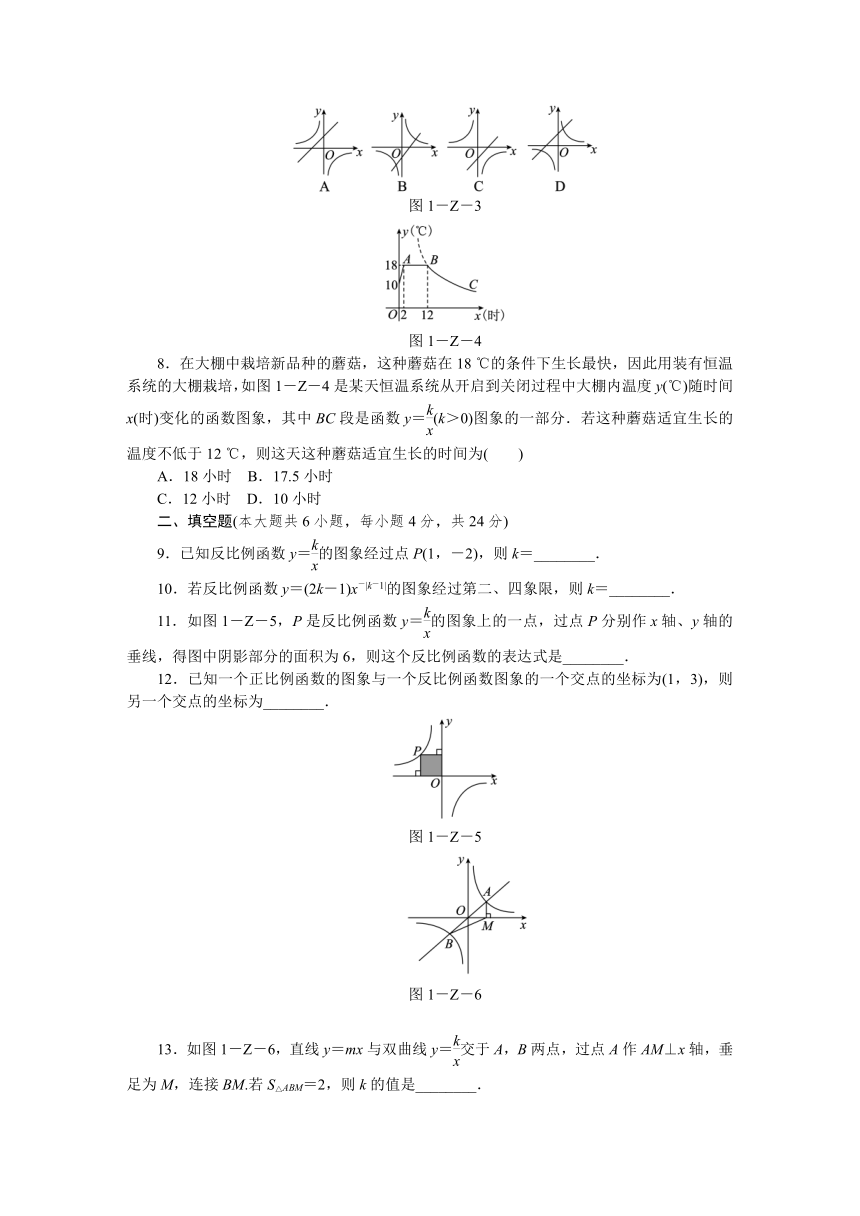
图1-Z-3
图1-Z-4
8.在大棚中栽培新品种的蘑菇,这种蘑菇在18 ℃的条件下生长最快,因此用装有恒温系统的大棚栽培,如图1-Z-4是某天恒温系统从开启到关闭过程中大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是函数y=(k>0)图象的一部分.若这种蘑菇适宜生长的温度不低于12 ℃,则这天这种蘑菇适宜生长的时间为( )
A.18小时 B.17.5小时
C.12小时 D.10小时
二、填空题(本大题共6小题,每小题4分,共24分)
9.已知反比例函数y=的图象经过点P(1,-2),则k=________.
10.若反比例函数y=(2k-1)x-|k-1|的图象经过第二、四象限,则k=________.
11.如图1-Z-5,P是反比例函数y=的图象上的一点,过点P分别作x轴、y轴的垂线,得图中阴影部分的面积为6,则这个反比例函数的表达式是________.
12.已知一个正比例函数的图象与一个反比例函数图象的一个交点的坐标为(1,3),则另一个交点的坐标为________.
图1-Z-5
图1-Z-6
13.如图1-Z-6,直线y=mx与双曲线y=交于A,B两点,过点A作AM⊥x轴,垂足为M,连接BM.若S△ABM=2,则k的值是________.
图1-Z-7
14.为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(min)的函数关系如图1-Z-7所示.已知,药物燃烧阶段,y与x成正比例,燃烧完后,y与x成反比例.现测得药物10 min燃烧完,此时教室内每立方米空气的含药量为8 mg.当每立方米空气中的含药量低于1.6 mg时,才能对人体无毒害作用.那么,从消毒开始,________min后教室内的空气才能达到安全要求.
三、解答题(本大题共4小题,共44分)
15.(10分)如图1-Z-8,已知反比例函数y=的图象经过点A(-3,-2).
(1)求反比例函数的表达式;
(2)若点B(1,m),C(3,n)在该函数的图象上,试比较m与n的大小.
图1-Z-8
16.(10分)已知反比例函数y=(m为常数,且m≠5).
(1)若在其图象的每个分支上,y随x的增大而增大,求m的取值范围;
(2)若其图象与一次函数y=-x+1图象的一个交点的纵坐标是3,求m的值.
17.(12分)如图1-Z-9,直线y=2x+3与y轴交于点A,与反比例函数y=(k>0)的图象交于点B,过点B作BC⊥x轴于点C,且点C的坐标为(1,0).
(1)求反比例函数的表达式.
(2)点D(a,1)是反比例函数y=(k>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
图1-Z-9
18.(12分)如图1-Z-10所示,制作一种产品的同时,需要将原材料加热,设该材料的温度为y(℃),从加热开始计算的时间为x(分).据了解,该材料在加热过程中温度y(℃)与时间x(分)成一次函数关系.已知该材料在加热前的温度为15 ℃,加热5分钟使材料温度达到60 ℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y(℃)与时间x(分)成反比例函数关系.
(1)分别求出该材料在加热和停止加热过程中,y与x之间的函数表达式(要求写出x的取值范围);
(2)根据工艺要求,在材料温度不低于30 ℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理可用的时间为多少分钟?
图1-Z-10
详解详析
1.B [解析] 选项B中y=是正比例函数.
2.B [解析] 把点(2,3)的坐标代入函数表达式y=,得k=6,∴反比例函数的表达式为y=,经验证,可知点(-2,-3)在这个函数图象上.故选B.
3.B 4.C
5.[全品导学号:46392035]A [解析] 由储存室的体积公式知:104=Sd,故储存室的底面积S(m2)与其深度d(m)之间的函数表达式为S=(d>0),为反比例函数.故选A.
6.A [解析] 反比例函数y=-中,k=-4<0,故其图象分布在第二、四象限内,所以在每一个象限内,y随x的增大而增大.又x1<x2<0,x3>0,所以0<y1<y2,y3<0,故有y37.C [解析] ∵k1<0<k2,b=-1<0,∴直线过第一、三、四象限,双曲线位于第二、四象限.故选C.
8.B [解析] 把B(12,18)的坐标代入y=,得
k=12×18=216.
设线段AD所在直线的函数表达式为y=mx+n,
把(0,10),(2,18)代入y=mx+n,
得解得
∴线段AD所在直线的函数表达式为y=4x+10.
当y=12时,12=4x+10,解得x=0.5,
12=,解得x=18,18-0.5=17.5.故选B.
9.-2 [解析] 把(1,-2)代入y=,得=-2,解得k=-2.
10.0 [解析] 因为y=(2k-1)x-是反比例函数,所以-=-1,解得k=0或k=2.又图象经过第二、四象限,所以2k-1<0,所以k<,故k=0.
11.y=- [解析] 设P(m,n),则阴影部分面积=-mn=6,即mn=-6,所以反比例函数的表达式为y=-.
12.[全品导学号:46392036](-1,-3)
[解析] ∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,∴另一个交点与点(1,3)关于原点对称,∴该点的坐标为(-1,-3).
13.2
14.50 [解析] 设药物燃烧完后y与x之间的函数表达式为y=,把(10,8)代入y=,
得8=,解得k=80,
∴y关于x的函数表达式为y=.
当y=1.6时,由1.6=,得x=50,
∴从消毒开始,50 min后教室内的空气才能达到安全要求.故答案为50.
15.解:(1)∵反比例函数y=的图象经过点A(-3,-2),∴k=-3×(-2)=6,
∴反比例函数的表达式为y=.
(2)∵k=6>0,
∴图象在第一、三象限,且在每一象限内,y随x的增大而减小.又∵0<1<3,
∴B(1,m),C(3,n)两个点都在第一象限,
∴m>n.
16.[全品导学号:46392037]解:(1)∵在反比例函数y=图象的每个分支上,y随x的增大而增大,
∴m-5<0,解得m<5.
(2)将y=3代入y=-x+1,得x=-2,
∴反比例函数y=的图象与一次函数y=-x+1图象的一个交点的坐标为(-2,3).
将(-2,3)代入y=,得3=,
解得m=-1.
17.解:(1)∵BC⊥x轴,且点C的坐标为(1,0),在y=2x+3中,当x=1时,y=5,∴点B的坐标为(1,5).
又∵点B(1,5)在反比例函数y=的图象上,
∴k=1×5=5,
∴反比例函数的表达式为y=.
(2)存在.将点D(a,1)的坐标代入y=,得a=5,
∴点D的坐标为(5,1).
设点D(5,1)关于x轴的对称点为D′,则点D′的坐标为(5,-1).
设过点B(1,5),点D′(5,-1)的直线的函数表达式为y=mx+b,
则解得
∴直线BD′的函数表达式为y=-x+.
根据题意,知直线BD′与x轴的交点即为所求点P.
当y=0时,-x+=0,解得x=,
故点P的坐标为(,0).
18.[全品导学号:46392038]解:(1)设加热过程中一次函数的表达式为y=kx+b(k≠0).
∵该函数的图象经过点(0,15),(5,60),
∴解得
∴一次函数的表达式为y=9x+15(0≤x≤5).
设停止加热后的反比例函数的表达式为y=(a≠0).
∵该函数的图象经过点(5,60),∴=60,
解得a=300,
∴反比例函数的表达式为y=(x>5).
(2)由y=9x+15=30,得x=;
由y==30,得x=10.而10-=.
∴对该材料进行特殊处理可用的时间为分钟.
一、选择题(本大题共8小题,每小题4分,共32分)
1.下列函数表达式中,y不是x的反比例函数的是( )
A.y= B.y=
C.y= D.xy=
2.已知反比例函数y=的图象经过点(3,2),那么下列四个点中,也在这个函数图象上的是( )
A.(3,-2) B.(-2,-3)
C.(1,-6) D.(-6,1)
3.若双曲线y=经过第二、四象限,则k的取值范围是( )
A.k> B.k<
C.k= D.不存在
4.对于函数y=-,下列说法错误的是 ( )
A. 它的图象分布在第二、四象限
B. 它的图象既是轴对称图形又是中心对称图形
C. 当x>0时,y的值随x的增大而减小
D. 当x<0时,y的值随x的增大而增大
图1-Z-1
5.如图1-Z-1,市煤气公司计划在地下修建一个容积为104 m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是( )
图1-Z-2
6.已知(x1,y1),(x2,y2),(x3,y3)是反比例函数y=-的图象上的三个点,且x1<x2<0,x3>0,则y1,y2,y3的大小关系是( )
A.y3<y1<y2 B.y2<y1<y3
C.y1<y2<y3 D.y3<y2<y1
7.已知k1<0<k2,则函数y=和y=k2x-1的图象大致是( )
图1-Z-3
图1-Z-4
8.在大棚中栽培新品种的蘑菇,这种蘑菇在18 ℃的条件下生长最快,因此用装有恒温系统的大棚栽培,如图1-Z-4是某天恒温系统从开启到关闭过程中大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是函数y=(k>0)图象的一部分.若这种蘑菇适宜生长的温度不低于12 ℃,则这天这种蘑菇适宜生长的时间为( )
A.18小时 B.17.5小时
C.12小时 D.10小时
二、填空题(本大题共6小题,每小题4分,共24分)
9.已知反比例函数y=的图象经过点P(1,-2),则k=________.
10.若反比例函数y=(2k-1)x-|k-1|的图象经过第二、四象限,则k=________.
11.如图1-Z-5,P是反比例函数y=的图象上的一点,过点P分别作x轴、y轴的垂线,得图中阴影部分的面积为6,则这个反比例函数的表达式是________.
12.已知一个正比例函数的图象与一个反比例函数图象的一个交点的坐标为(1,3),则另一个交点的坐标为________.
图1-Z-5
图1-Z-6
13.如图1-Z-6,直线y=mx与双曲线y=交于A,B两点,过点A作AM⊥x轴,垂足为M,连接BM.若S△ABM=2,则k的值是________.
图1-Z-7
14.为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y(mg)与时间x(min)的函数关系如图1-Z-7所示.已知,药物燃烧阶段,y与x成正比例,燃烧完后,y与x成反比例.现测得药物10 min燃烧完,此时教室内每立方米空气的含药量为8 mg.当每立方米空气中的含药量低于1.6 mg时,才能对人体无毒害作用.那么,从消毒开始,________min后教室内的空气才能达到安全要求.
三、解答题(本大题共4小题,共44分)
15.(10分)如图1-Z-8,已知反比例函数y=的图象经过点A(-3,-2).
(1)求反比例函数的表达式;
(2)若点B(1,m),C(3,n)在该函数的图象上,试比较m与n的大小.
图1-Z-8
16.(10分)已知反比例函数y=(m为常数,且m≠5).
(1)若在其图象的每个分支上,y随x的增大而增大,求m的取值范围;
(2)若其图象与一次函数y=-x+1图象的一个交点的纵坐标是3,求m的值.
17.(12分)如图1-Z-9,直线y=2x+3与y轴交于点A,与反比例函数y=(k>0)的图象交于点B,过点B作BC⊥x轴于点C,且点C的坐标为(1,0).
(1)求反比例函数的表达式.
(2)点D(a,1)是反比例函数y=(k>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
图1-Z-9
18.(12分)如图1-Z-10所示,制作一种产品的同时,需要将原材料加热,设该材料的温度为y(℃),从加热开始计算的时间为x(分).据了解,该材料在加热过程中温度y(℃)与时间x(分)成一次函数关系.已知该材料在加热前的温度为15 ℃,加热5分钟使材料温度达到60 ℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y(℃)与时间x(分)成反比例函数关系.
(1)分别求出该材料在加热和停止加热过程中,y与x之间的函数表达式(要求写出x的取值范围);
(2)根据工艺要求,在材料温度不低于30 ℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理可用的时间为多少分钟?
图1-Z-10
详解详析
1.B [解析] 选项B中y=是正比例函数.
2.B [解析] 把点(2,3)的坐标代入函数表达式y=,得k=6,∴反比例函数的表达式为y=,经验证,可知点(-2,-3)在这个函数图象上.故选B.
3.B 4.C
5.[全品导学号:46392035]A [解析] 由储存室的体积公式知:104=Sd,故储存室的底面积S(m2)与其深度d(m)之间的函数表达式为S=(d>0),为反比例函数.故选A.
6.A [解析] 反比例函数y=-中,k=-4<0,故其图象分布在第二、四象限内,所以在每一个象限内,y随x的增大而增大.又x1<x2<0,x3>0,所以0<y1<y2,y3<0,故有y3
8.B [解析] 把B(12,18)的坐标代入y=,得
k=12×18=216.
设线段AD所在直线的函数表达式为y=mx+n,
把(0,10),(2,18)代入y=mx+n,
得解得
∴线段AD所在直线的函数表达式为y=4x+10.
当y=12时,12=4x+10,解得x=0.5,
12=,解得x=18,18-0.5=17.5.故选B.
9.-2 [解析] 把(1,-2)代入y=,得=-2,解得k=-2.
10.0 [解析] 因为y=(2k-1)x-是反比例函数,所以-=-1,解得k=0或k=2.又图象经过第二、四象限,所以2k-1<0,所以k<,故k=0.
11.y=- [解析] 设P(m,n),则阴影部分面积=-mn=6,即mn=-6,所以反比例函数的表达式为y=-.
12.[全品导学号:46392036](-1,-3)
[解析] ∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,∴另一个交点与点(1,3)关于原点对称,∴该点的坐标为(-1,-3).
13.2
14.50 [解析] 设药物燃烧完后y与x之间的函数表达式为y=,把(10,8)代入y=,
得8=,解得k=80,
∴y关于x的函数表达式为y=.
当y=1.6时,由1.6=,得x=50,
∴从消毒开始,50 min后教室内的空气才能达到安全要求.故答案为50.
15.解:(1)∵反比例函数y=的图象经过点A(-3,-2),∴k=-3×(-2)=6,
∴反比例函数的表达式为y=.
(2)∵k=6>0,
∴图象在第一、三象限,且在每一象限内,y随x的增大而减小.又∵0<1<3,
∴B(1,m),C(3,n)两个点都在第一象限,
∴m>n.
16.[全品导学号:46392037]解:(1)∵在反比例函数y=图象的每个分支上,y随x的增大而增大,
∴m-5<0,解得m<5.
(2)将y=3代入y=-x+1,得x=-2,
∴反比例函数y=的图象与一次函数y=-x+1图象的一个交点的坐标为(-2,3).
将(-2,3)代入y=,得3=,
解得m=-1.
17.解:(1)∵BC⊥x轴,且点C的坐标为(1,0),在y=2x+3中,当x=1时,y=5,∴点B的坐标为(1,5).
又∵点B(1,5)在反比例函数y=的图象上,
∴k=1×5=5,
∴反比例函数的表达式为y=.
(2)存在.将点D(a,1)的坐标代入y=,得a=5,
∴点D的坐标为(5,1).
设点D(5,1)关于x轴的对称点为D′,则点D′的坐标为(5,-1).
设过点B(1,5),点D′(5,-1)的直线的函数表达式为y=mx+b,
则解得
∴直线BD′的函数表达式为y=-x+.
根据题意,知直线BD′与x轴的交点即为所求点P.
当y=0时,-x+=0,解得x=,
故点P的坐标为(,0).
18.[全品导学号:46392038]解:(1)设加热过程中一次函数的表达式为y=kx+b(k≠0).
∵该函数的图象经过点(0,15),(5,60),
∴解得
∴一次函数的表达式为y=9x+15(0≤x≤5).
设停止加热后的反比例函数的表达式为y=(a≠0).
∵该函数的图象经过点(5,60),∴=60,
解得a=300,
∴反比例函数的表达式为y=(x>5).
(2)由y=9x+15=30,得x=;
由y==30,得x=10.而10-=.
∴对该材料进行特殊处理可用的时间为分钟.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
