九年级二次函数求解析式和面积专题

中小学教育资源及组卷应用平台




【教学目标】
1、熟悉各种求解二次函数解析式的方法；
2、在不同场景中二次函数三种解析式的应用；
3、二次函数中典型面积问题的处理。
【教学重难点】
1、求二次函数解析式方法的灵活运用；
2、二次函数面积问题的解题思路。
【教学内容】
1、求二次函数解析式
1、三点型
若已知二次函数图像上任意三点的坐标，则可以用一般式y= ax2 +bx+c.
解题策略：通过各种途径搜索题目的各个信息找到三个点的坐标，然后用待定系数法球解析式，此类问题是中考中考得最频繁的一类。
例1、 将直角边长为6的等腰Rt△AOC放在如图所示的平面直角坐标系中，点O为坐标原点，点C、A分别在x、y轴的正半轴上，一条抛物线经过点A、C及点B(–3，0)． 求该抛物线的解析式；
解：由题意知：A（0，6），C（6，0），
设经过点A、B、C的抛物线解析式为y=ax2+bx+c,
则：
解得：
∴该抛物线的解析式为
例2、如图，在直角坐标系中，A（-1，0），B（0，2），一动点P沿过B点且垂直于AB的射线BM运动，P点的运动速度为每秒1个单位长度，射线BM与x轴交与点C．
（1）求点C的坐标．
（2）求过点A、B、C三点的抛物线的解析式．

解：（1）点C的坐标是（4，0）；
（2）设过点A、B、C三点的抛物线的解析式为y=ax2+bx+c（a≠0），将点A、B、C三点的坐标代入得：
解得，∴抛物线的解析式是：y= x2+x+2．

2、顶点型
若直接或间接已知二次函数图像的顶点坐标，则可以用顶点式y=a(x-h)2+k.
解题策略：想方设法找到顶点的坐标，然后用待定系数法球解析式，此法比较简单。
例3 、如图，四边形ABCD是菱形，点D的坐标是，以点C为顶点的抛物线 恰好经过轴上A、B两点．
(1) 求A、B、C三点的坐标；
(2) 求经过A、B、C三点的的抛物线的解析式；
(3) 若将上述抛物线沿其对称轴向上平移后恰好过D点，求平移后抛物线的解析式，并指出平移了多少各单位？


解：(1)由抛物线的对称性可知AM=BM．
在Rt△AOD和Rt△BMC中，
∵OD=MC，AD=BC，
∴△AOD≌△BMC
∴OA=MB=MA
设菱形的边长为2m，在Rt△AOD中，
，解得．
∴DC=2，OA=1，OB=3．
∴A、B、C三点的坐标分别为、、
(2)设抛物线的解析式为，带入A点的坐标，得
∴抛物线的解析式为
(3) 设抛物线的解析式为，代入D点的坐标，得
∴平移后的抛物线的解析式为
∴平移了个单位．

3、交点型
若直接或间接已知二次函数图像与x轴的两交点坐标，则可以用交点式y=a(x-x1)·(x-x2).
解题策略：要注意题目所给的点的坐标特征，如果已知或可求出与x轴的交点坐标（纵坐标为0），就可以采用此法。
例4、 如下图，二次函数y=ax2+bx+c的图像与x轴交于A、B两点，与y轴交于C点，若AC=20，BC=15，∠ABC=90°，求这个二次函数解析式.
解：在Rt△ABC中，AB=+=25，
∵S△ABC=AC·BC=AB·OC，
∴OC===12.
∵AC2=AO·AB， ∴OA===16，
∴OB=9.
从而得A、B、C三点坐标分别为（-16，0）、（9，0）、（0，12）.
于是，利用交点型可求得函数解析式为：y=-x2-x+12.

4、混合型
解题策略：选用合适的方法综合利用题目所给条件。抛物线的顶点坐标为，这是中考中最多的题型。
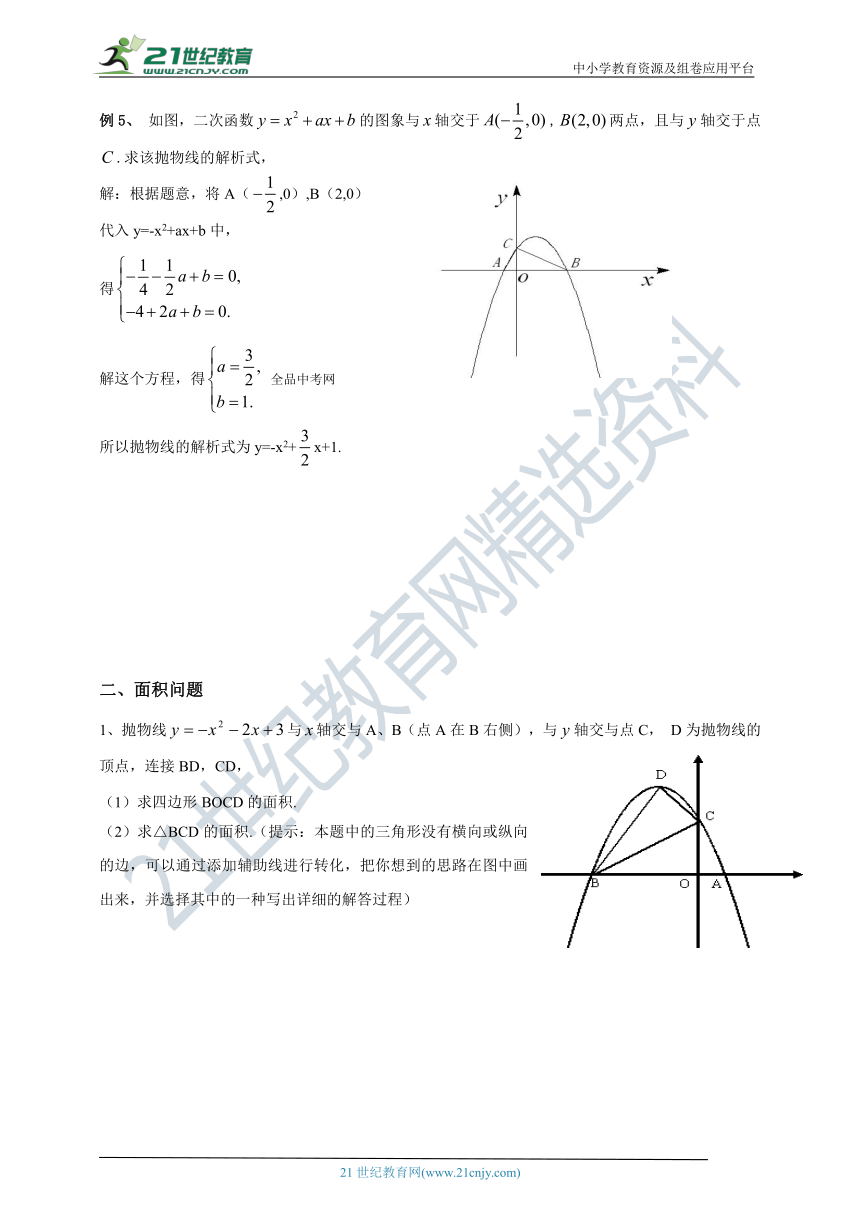
例5、 如图，二次函数的图象与轴交于,两点，且与轴交于点.求该抛物线的解析式，
解：根据题意，将A（,0）,B（2,0）
代入y=-x2+ax+b中，
得
解这个方程，得 全品中考网 (?http:?/??/?zk.canpoint.cn?/??)
所以抛物线的解析式为y=-x2+x+1.






2、面积问题
1、抛物线与轴交与A、B（点A在B右侧），与轴交与点C， D为抛物线的顶点，连接BD，CD，
（1）求四边形BOCD的面积.
（2）求△BCD的面积.（提示：本题中的三角形没有横向或纵向的边，可以通过添加辅助线进行转化，把你想到的思路在图中画出来，并选择其中的一种写出详细的解答过程）







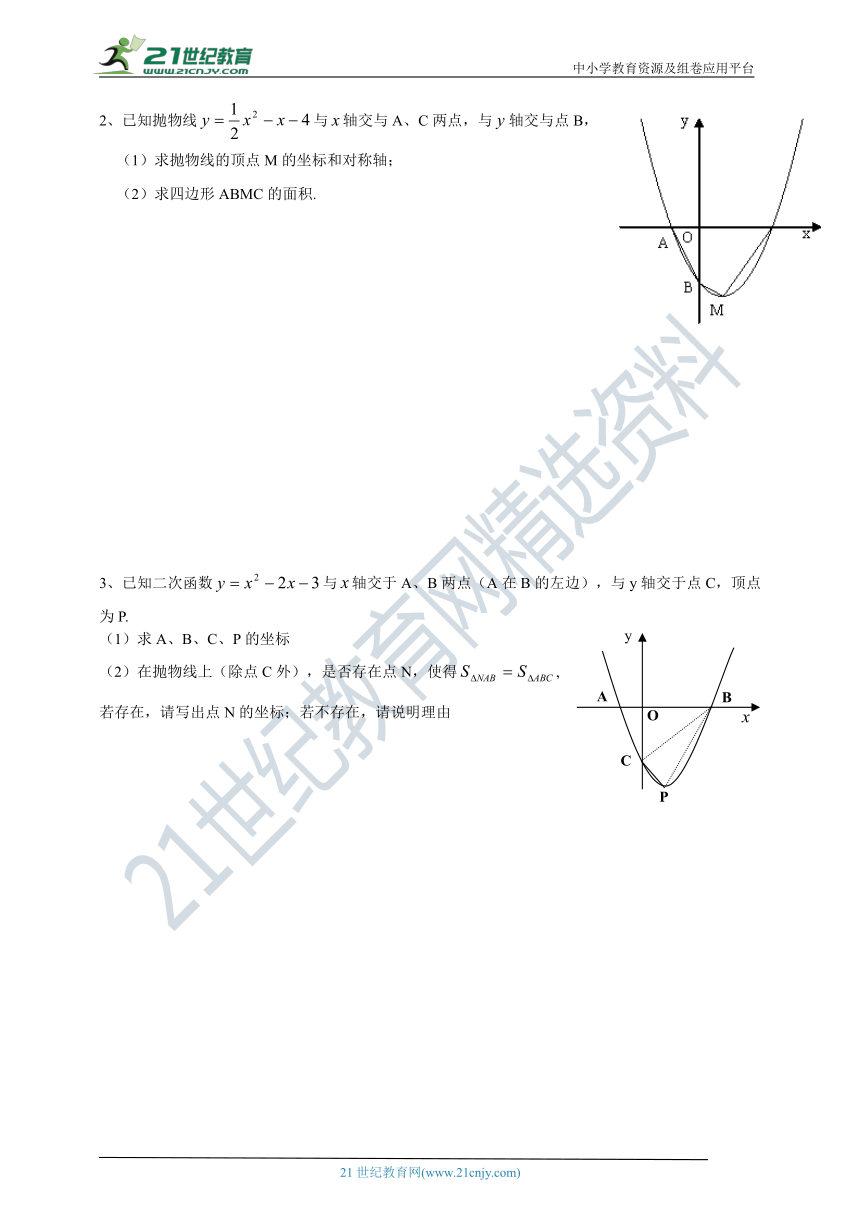
2、已知抛物线与轴交与A、C两点，与轴交与点B，
（1）求抛物线的顶点M的坐标和对称轴；
（2）求四边形ABMC的面积.















3、已知二次函数与轴交于A、B两点（A在B的左边），与y轴交于点C，顶点为P.
（1）求A、B、C、P的坐标
（2）在抛物线上（除点C外），是否存在点N，使得,
若存在，请写出点N的坐标；若不存在，请说明理由












4、抛物线与轴交与A、B（点A在B右侧），与轴交与点C，若点E为第二象限抛物线上一动点， 点E运动到什么位置时，△EBC的面积最大,并求出此时点E的坐标和△EBC的最大面积．
提示：点E的坐标可以设为（），x的取值范围是-3＜x＜0,根据题2求三角形面积的思路建立△EBC的面积关于x的函数关系式，体会点E位置的不确定性对方法的选择是否有影响．























【课后作业】
1.已知二次函数y=ax2＋bx＋c，当 x=0时，y=0；x=1时，y=2；x=-1时，y=1．求a、b、c，并写出函数解析式．






2．把抛物线y＝(x－1)2沿y轴向上或向下平移后所得抛物线经过点Q(3，0)，求平移后的抛物线的解析式．





3．二次函数y＝x2－mx＋m－2的图象的顶点到x轴的距离为求二次函数解析式．








4．已知二次函数的最小值为1，求m的值．









5．已知抛物线y＝ax2经过点A(2，1)．
(1)求这个函数的解析式；
(2)写出抛物线上点A关于y轴的对称点B的坐标；
(3)求△OAB的面积；
(4)抛物线上是否存在点C，使△ABC的面积等于△OAB面积的一半，若存在，求出C点的坐标；若不存在，请说明理由．












6、在体育测试时，初三的一名高个子男生推铅球，已知铅球所经过的路线是某个二次函数图象的一部分，如图所示，如果这名男同学出手处A点的坐标为（0,2），铅球路线的最高处B点的坐标为（6,5）。
（1）求这个二次函数的解析式；
（2）该同学把铅球推出多远？（精确到0.01米，提示：）












7．函数y＝x2＋2x－3(－2≤x≤2)的最大值和最小值分别为( )
A．4和－3 B．5和－3 C．5和－4 D．－1和4

8．如图，有一座抛物线型拱桥，已知桥下在正常水位AB时，水面宽8m，水位上升3m， 就达到警戒水位CD，这时水面宽4m，若洪水到来时，水位以每小时0.2m的速度上升，求水过警戒水位后几小时淹到桥拱顶．










9．抛物线y＝ax2＋bx＋c(a≠0)的图象如下图所示，那么a（ ）0，b（ ）0，c（）0

10．二次函数y＝mx2＋2mx－(3－m)的图象如下图所示，那么m的取值范围是( )

A．m＞0 B．m＞3
C．m＜0 D．0＜m＜3




11．在同一坐标系内，函数y＝kx2和y＝kx－2(k≠0)的图象大致如图( )

12.已知抛物线y=-x2+mx+n的顶点坐标是（-1，- 3 )，则m和n的值分别是（ ）
A.2,4 B.-2,-4 C.2,-4 D.-2,0
13.已知二次函数的图象经过原点和第一、二、三象限，则（ ）
（A） （B）
（C） （D）

15．如图，抛物线y=ax2+bx+c（a，b，c是常数，a≠0）与x轴交于A，B两点，与y轴交于点C，三个交点的坐标分别为A（﹣1，0），B（3，0），C（0，3）．
（1）求抛物线的解析式及顶点D的坐标；
（2）若P为线段BD上的一个动点，过点P作PM⊥x轴于点M，求四边形PMAC面积的最大值和此时P点的坐标；
（3）若P为抛物线在第一象限上的一个动点，过点P作PQ∥AC交x轴于点Q．当点P的坐标为　_________　时，四边形PQAC是平行四边形；当点P的坐标为　_________　时，四边形PQAC是等腰梯形（直接写出结果，不写求解过程）．




　16、已知抛物线与轴交于A、B两点（点A在点B的左侧），与y轴交于点C。
（1）求点A、B、C的坐标；
（2）设点D在已知抛物线的对称轴上，当⊿BCD的面积与⊿ACB的面积相等时，求点D的坐标；
（3）若点P在已知抛物线对称轴上，当∠BPC为钝角时，试求点P纵坐标的取值范围。





17、如图，平移抛物线使它经过坐标原点O和A(6，0)，顶点M；经过点M且平行于y轴的直线交抛物线于点P。（1）顶点M是 ；（2）阴影部分的面积是 。










18、如图，抛物线与直线交于点A、B，点M是抛物线上的一个动点，连接OM
（1）当M为抛物线的顶点时，求⊿OMB的面积；
（2）当⊿OMB的面积为10时，求点M的坐标；
（3）当点M在直线AB的下方且在抛物线对称轴的右侧，M运动到何处时，⊿OMB的面积最大。


























二次函数求解析式和面积专题





C

P



O

A

B

y



21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)