北师大九年级概率单元测试(含答案与解析)
文档属性
| 名称 | 北师大九年级概率单元测试(含答案与解析) |  | |
| 格式 | zip | ||
| 文件大小 | 268.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-01 09:00:52 | ||
图片预览



文档简介
北师大九年级概率单元测试
副标题
题号 一 二 三 总分
得分
一、选择题(本大题共12小题,共36.0分)
三张外观相同的卡片分别标有数字1、2、3,从中随机一次抽出两张,这两张卡片上的数字恰好都小于3的概率是( )
A. B. C. D.
一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球后不放回,再随机摸出一个小球,则两次摸出的小球标号之和等于5的概率为( )
A. B. C. D.
“六?一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法不正确的是( )
????转动转盘的次数n ?100 ?150 ?200 ?500 ?800 ?1000
??落在“铅笔”区域的次数m ??68 ??108 ??140 ??355 ??560 ??690
??落在“铅笔”区域的频率 ?0.68 ?0.72 ?0.70 ?0.71 ?0.70 ?0.69
A. 当n很大时,估计指针落在“铅笔”区域的频率大约是
B. 假如你去转动转盘一次,获得铅笔的概率大约是
C. 如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次
D. 转动转盘10次,一定有3次获得文具盒
从长为3,5,7,10的四条线段中任意选取三条作为边,能构成三角形的概率是( )
A. B. C. D. 1
如图,两个转盘分别自由转动一次,当停止转动时,两个转盘的指针都指向2的概率为( )
A. B. C. D.
一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为( )
A. 20 B. 24 C. 28 D. 30
现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )
A. B. C. D.
袋内装有标号分别为1、2、3、4的4个小球,从袋内随机取出一个小球,让其标号为一个两位数的十位数字,放回搅匀后,再随机取出一个小球,让其标号为这个两位数的个位数字,则组成的两位数是3的倍数的概率为( )
A. B. C. D.
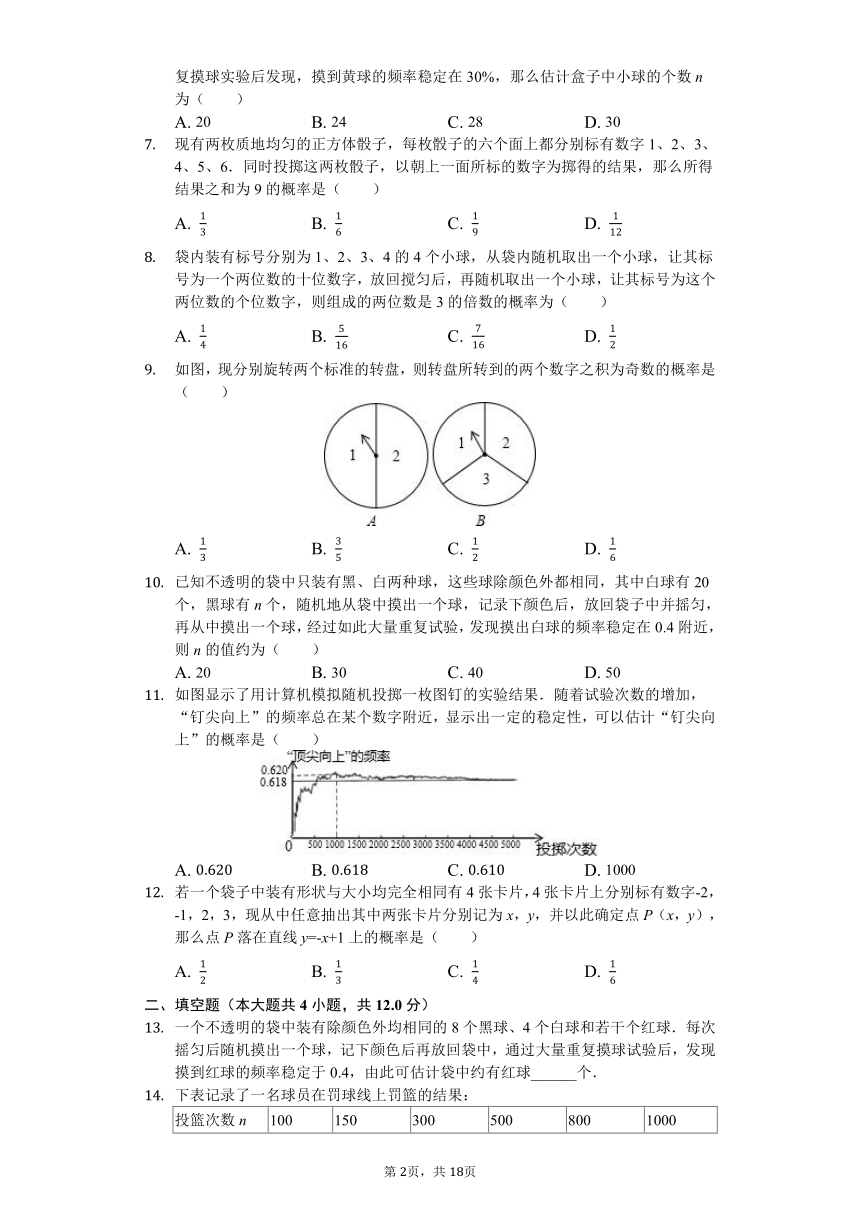
如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是( )
A. B. C. D.
已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有20个,黑球有n个,随机地从袋中摸出一个球,记录下颜色后,放回袋子中并摇匀,再从中摸出一个球,经过如此大量重复试验,发现摸出白球的频率稳定在0.4附近,则n的值约为( )
A. 20 B. 30 C. 40 D. 50
如图显示了用计算机模拟随机投掷一枚图钉的实验结果.随着试验次数的增加,“钉尖向上”的频率总在某个数字附近,显示出一定的稳定性,可以估计“钉尖向上”的概率是( )
A. B. C. D. 1000
若一个袋子中装有形状与大小均完全相同有4张卡片,4张卡片上分别标有数字-2,-1,2,3,现从中任意抽出其中两张卡片分别记为x,y,并以此确定点P(x,y),那么点P落在直线y=-x+1上的概率是( )
A. B. C. D.
二、填空题(本大题共4小题,共12.0分)
一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球.每次摇匀后随机摸出一个球,记下颜色后再放回袋中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.4,由此可估计袋中约有红球______个.
下表记录了一名球员在罚球线上罚篮的结果:
投篮次数n 100 150 300 500 800 1000
投中次数m 58 96 174 302 484 601
投中频率 0.580 0.640 0.580 0.604 0.605 0.601
这名球员投篮一次,投中的概率约是______ .
在四张完全相同的卡片上分别印有等边三角形、平行四边形、矩形、圆的图案,现将印有图案的一面朝下,混合后从中一次性随机抽取两张,则抽到的卡片上印有的图案都是轴对称图形的概率为______.
从-1,0,2,3这四个数中,任取两个数作为a,b,分别代入一元二次方程ax2+bx+2=0中,那么所有可能的一元二次方程中有实数解的一元二次方程的概率为______ .
三、解答题(本大题共7小题,共56.0分)
一个不透明的口袋中装有4个分别标有数字-1,-2,3,4的小球,它们的形状、大小完全相同.先从口袋中随机摸出一个小球,记下数字为x;再在剩下的3个小球中随机摸出一个小球,记下数字为y,得到点P的坐标(x,y).
(1)请用“列表”或“画树状图”等方法表示出点P(x,y)所有可能的结果;
(2)求出点P(x,y)在第一象限或第三象限的概率.
在课堂上,老师将除颜色外都相同的1个黑球和若干个白球放入一个不透明的口袋并搅匀,让全班同学依次进行摸球试验,每次随机摸出一个球,记下颜色再放回搅匀,下表是试验得到的一组数据.
摸球的次数n 100 150 200 500 800
摸到黑球的次数m 26 37 49 124 200
摸到黑球的频率 0.26 0.247 0.245 0.248 a
(1)表中a的值等于______;
(2)估算口袋中白球的个数;
(3)用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
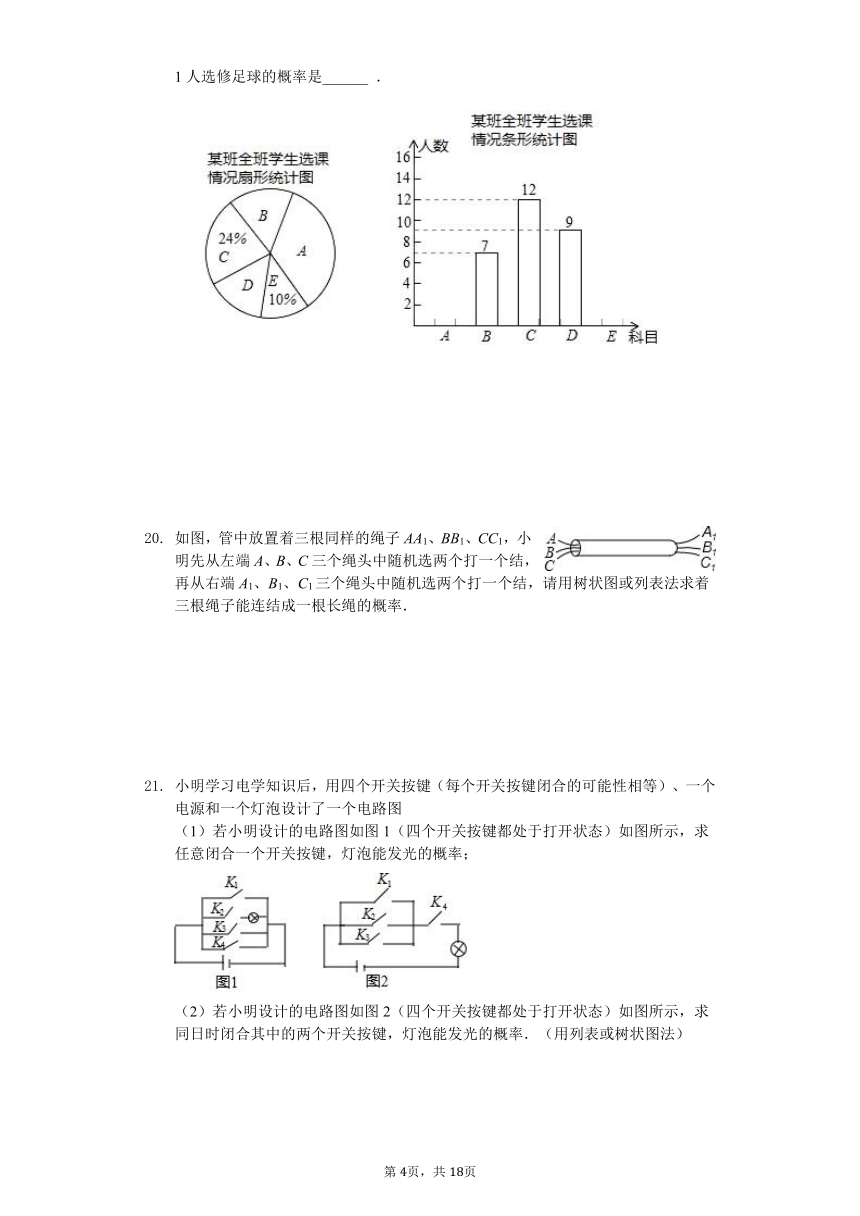
我市某校在推进新课改的过程中,开设的体育选修课有:A:篮球,B:足球,C:排球,D:羽毛球,E:乒乓球,学生可根据自己的爱好选修一门,学校李老师对某班全班学生的选课情况进行调查统计,制成了两幅不完整的统计图(如图).
(1)该班的总人数为______ 人,并补全频数分布直方图;
(2)表示“足球”所在扇形的圆心角是______ °.
(3)该班班委4人中,1人选修篮球,2人选修足球,1人选修排球,李老师要从这4人中任选2人了解他们对体育选修课的看法,则选出的2人恰好1人选修篮球,1人选修足球的概率是______ .
如图,管中放置着三根同样的绳子AA1、BB1、CC1,小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,请用树状图或列表法求着三根绳子能连结成一根长绳的概率.
小明学习电学知识后,用四个开关按键(每个开关按键闭合的可能性相等)、一个电源和一个灯泡设计了一个电路图
(1)若小明设计的电路图如图1(四个开关按键都处于打开状态)如图所示,求任意闭合一个开关按键,灯泡能发光的概率;
(2)若小明设计的电路图如图2(四个开关按键都处于打开状态)如图所示,求同日时闭合其中的两个开关按键,灯泡能发光的概率.(用列表或树状图法)
端午节当天,小丽的妈妈从超市买了一些粽子回家并用不透明的袋子装着(除味道不同外,其它均相同).小丽问买了什么味道的粽子,妈妈说:“其中两个是大枣味的,剩余是火腿味的”,若小丽从袋中任意拿出一个粽子是大枣味的概率为.
(1)求袋子中火腿味粽子的个数;
(2)请用画树状图或列表的方法求连续2次(每次拿1个)拿到的两个棕子恰好是同一味道的概率.
张老师为了解学生完成数学课前预习的具体情况,对部分学生进行了跟踪调查,并将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)C类中女生有______名,D类中男生有______名,将下面条形统计图补充完整;
(2)若该校九年级共有女生180名,则九年级女生完成数学作业达到很好和较好的公约多少人?
(3)为了共同进步,张老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好性别相同的概率.
答案和解析
1.【答案】A
【解析】
解:画树状图得:
∵共有6种等可能的结果,而两张卡片上的数字恰好都小于3有2种情况,
∴两张卡片上的数字恰好都小于3概率==.
故选:A.
首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两张卡片上的数字恰好都小于3的情况,再利用概率公式即可求得答案.
此题考查的是用列表法或树状图法求概率.解题的关键是要注意是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
2.【答案】C
【解析】
解:画树状图得:
∵共有12种等可能的结果,两次摸出的小球标号之和等于5的有4种情况,
∴两次摸出的小球标号之和等于5的概率是:=.
故选:C.
首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的小球标号之和等于5的情况,再利用概率公式求解即可求得答案.
此题考查了列表法或树状图法求概率.当有两个元素时,可用树形图列举,也可以列表列举.解题时注意:概率=所求情况数与总情况数之比.
3.【答案】D
【解析】
解:A、频率稳定在0.7左右,故用频率估计概率,指针落在“铅笔”区域的频率大约是0.70,故A选项正确;
由A可知B、转动转盘一次,获得铅笔的概率大约是0.70,故B选项正确;
C、指针落在“文具盒”区域的概率为0.30,转动转盘2000次,指针落在“文具盒”区域的次数大约有2000×0.3=600次,故C选项正确;
D、随机事件,结果不确定,故D选项正确.
故选:D.
根据图表可求得指针落在铅笔区域的概率,另外概率是多次实验的结果,因此不能说转动转盘10次,一定有3次获得文具盒.
本题要理解用面积法求概率的方法.注意概率是多次实验得到的一个相对稳定的值.
4.【答案】B
【解析】
解:从长为3,5,7,10的四条线段中任意选取三条作为边,所有等可能情况有:3,5,7;3,5,10;3,7,10;5,7,10,共4种,
其中能构成三角形的情况有:3,5,7;5,7,10,共2种,
则P(能构成三角形)==,
故选:B.
列举出所有等可能的情况数,找出能构成三角形的情况数,即可求出所求概率.
此题考查了列表法与树状图法,以及三角形的三边关系,其中概率=所求情况数与总情况数之比.
5.【答案】D
【解析】
解:列表如下:
? 1 2 3 4
1 (1,1) (2,1) (3,1) (4,1)
2 (1,2) (2,2) (3,2) (4,2)
3 (1,3) (2,3) (3,3) (4,3)
4 (1,4) (2,4) (3,4) (4,4)
∵共有16种等可能的结果,两个转盘的指针都指向2的只有1种结果,
∴两个转盘的指针都指向2的概率为,
故选:D.
首先根据题意列出表格,然后由表格即可求得所有等可能的结果与都指向2的情况数,继而求得答案.
此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
6.【答案】D
【解析】
解:根据题意得=30%,解得n=30,
所以这个不透明的盒子里大约有30个除颜色外其他完全相同的小球.
故选:D.
根据利用频率估计概率得到摸到黄球的概率为30%,然后根据概率公式计算n的值.
本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.当实验的所有可能结果不是有限个或结果个数很多,或各种可能结果发生的可能性不相等时,一般通过统计频率来估计概率.
7.【答案】C
【解析】
解:由题意可得,
同时投掷这两枚骰子,所得的所有结果是:
(1,1)、(1,2)、(1,3)、(1,4)、(1,5)、(1,6)、
(2,1)、(2,2)、(2,3)、(2,4)、(2,5)、(2,6)、
(3,1)、(3,2)、(3,3)、(3,4)、(3,5)、(3,6)、
(4,1)、(4,2)、(4,3)、(4,4)、(4,5)、(4,6)、
(5,1)、(5,2)、(5,3)、(5,4)、(5,5)、(5,6)、
(6,1)、(6,2)、(6,3)、(6,4)、(6,5)、(6,6),
则所有结果之和是:
2、3、4、5、6、7、
3、4、5、6、7、8、
4、5、6、7、8、9、
5、6、7、8、9、10、
6、7、8、9、10、11、
7、8、9、10、11、12,
∴所得结果之和为9的概率是:,
故选C.
根据题意可以通过列表的方法写出所有的可能性,从而可以得到所得结果之和为9的概率.
本题考查列表法和树状图法,解题的关键是明确题意,列出相应的表格,计算出相应的概率.
8.【答案】B
【解析】
解:画树状图为:
共有16种等可能的结果数,其中所成的两位数是3的倍数的结果数为5,
所以成的两位数是3的倍数的概率=.
故选:B.
画树状图展示所有16种等可能的结果数,再找出所成的两位数是3的倍数的结果数,然后根据概率公式求解.
本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率..
9.【答案】A
【解析】
解:画树状图得:
∵共有6种等可能的结果,转盘所转到的两个数字之积为奇数的有2种情况,
∴转盘所转到的两个数字之积为奇数的概率是:=.
故选:A.
首先根据题意画出树状图,然后由树状图求得所有等可能的结果与转盘所转到的两个数字之积为奇数的情况,再利用概率公式求解即可求得答案.
此题考查了列表法或树状图法求概率.注意此题属于放回实验,用到的知识点为:概率=所求情况数与总情况数之比.
10.【答案】B
【解析】
解:根据题意得=0.4,
解得:n=30,
故选:B.
根据白球的频率稳定在0.4附近得到白球的概率约为0.4,根据概率公式列出方程求解可得.
此题考查了利用频率估计概率,解答此题的关键是了解白球的频率稳定在0.4附近即为概率约为0.4.
11.【答案】B
【解析】
解:由图象可知随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618.
故选:B.
结合给出的图形以及在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,解答即可.
本题比较容易,考查利用频率估计概率.大量反复试验下频率稳定值即概率.用到的知识点为:概率=所求情况数与总情况数之比.
12.【答案】B
【解析】
解:画树状图如下:
由树状图可知共有12种等可能结果,其中点P落在直线y=-x+1上的有(-2,3)、(-1,2)、(2,-1)、(3,-2),
所以点P落在直线y=-x+1上的概率是=,
故选:B.
画出树状图,再求出在直线上的点的坐标的个数,然后根据概率公式列式计算即可得解.
本题考查了列表法与树状图法,一次函数图象上点的坐标特征,用到的知识点为:概率=所求情况数与总情况数之比.
13.【答案】8
【解析】
解:由题意可得,
摸到黑球和白球的频率之和为:1-0.4=0.6,
∴总的球数为:(8+4)÷0.6=20,
∴红球有:20-(8+4)=8(个),
故答案为:8.
根据摸到红球的频率,可以得到摸到黑球和白球的概率之和,从而可以求得总的球数,从而可以得到红球的个数.
本题考查利用频率估计概率,解题的关键是明确题意,找出所求问题需要的条件.
14.【答案】0.6
【解析】
解:由频率分布表可知,随着投篮次数越来越大时,频率逐渐稳定到常数0.6附近,
这名球员投篮一次,投中的概率约是0.6,
故答案为:0.6.
根据频率估计概率的方法结合表格可得答案.
此题考查了利用频率估计概率的知识,注意这种概率的得出是在大量实验的基础上得出的,不能单纯的依靠几次决定.
15.【答案】
【解析】
解:等边三角形、矩形和圆是轴对称图形,
用A、B、C、D分别表示等边三角形、平行四边形、矩形、圆,
画树状图如下:
共有12种等可能的结果数,其中抽到的卡片上印有的图案都是轴对称图形有6种结果,
所以抽到的卡片上印有的图案都是轴对称图形的概率为=.
故答案为:
根据轴对称图形的定义得到等边三角形、矩形和圆是轴对称图形,然后用A、B、C、D分别表示等边三角形、平行四边形、矩形、圆,画树状图展示所有12种等可能的结果数,其中抽到的卡片上印有的图案都是轴对称图形有6种,再利用概率的定义计算即可.
本题考查了利用列表或树状图求概率的方法:先通过列表或树状图展示所有等可能的结果数n,再找出其中某事件所占有的结果数m,然后根据概率的概念计算这个事件的概率为P=.
16.【答案】
【解析】
解:画树状图得:
则共有12种等可能的结果,
∵一元二次方程ax2+bx+2=0有实数解,
∴a≠0,且△=b2-8a≥0,
∴所有可能的一元二次方程中有实数解的一元二次方程的有3种情况,
∴所有可能的一元二次方程中有实数解的一元二次方程的概率为:=.
故答案为:.
首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所有可能的一元二次方程中有实数解的一元二次方程的情况,再利用概率公式即可求得答案.
本题考查的是用列表法或画树状图法求概率以及一元二次方程根的情况.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
17.【答案】解:(1)列表如下:
-1 -2 3 4
-1 (-1,-2) (-1,3) (-1,4)
-2 (-2,-1) (-2,3) (-2,4)
3 (3,-1) (3,-2) (3,4)
4 (4,-1) (4,-2) (4,3)
(2)从上面的表格可以看出,所有可能出现的结果共有12种,且每种结果出现的可能性相同,其中点(x,y)在第一象限或第三象限的结果有4种,所以其的概率==.
【解析】
(1)通过列表展示即可得到所有可能的结果;
(2)找出在第一象限或第三象限的结果数,然后根据概率公式计即可.
本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率
18.【答案】0.25
【解析】
解:(1)由题意可得:a=200÷800=0.25;
故答案为:0.25;
(2)又表格中数据可得出,摸到黑球的频率稳定在0.25,
故1÷0.25-1=3(个),
答:口袋中白球的个数为3个;
(3)画树状图得:
∵共有16种等可能的结果,两次都摸到白球的有9种情况,
∴两次都摸到白球的概率为:.
(1)直接利用频数÷总数=频率求出答案;
(2)直接利用表格中数据估算出得到白球的频率,进而得出答案;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次都摸到白球的情况,再利用概率公式即可求得答案.
此题考查了模拟实验以及频率求法和树状图法与列表法求概率,用到的知识点为:概率=所求情况数与总情况数之比.
19.【答案】50;50.4;
【解析】
解:(1)该班的总人数为12÷24%=50(人),
E科目人数为50×10%=5(人),A科目人数为50-(7+12+9+5)=17(人),
补全图形如下:
故答案为:50;
(2)表示“足球”所在扇形的圆心角是360°×=50.4°,
故答案为:50.4;
(3)画树状图为:
共有12种等可能的结果数,其中选出的2人恰好1人选修篮球,1人选修足球占4种,
所以选出的2人恰好1人选修篮球,1人选修足球的概率==,
故答案为:.
(1)用C组的人数除以它所占的百分比即可得到全班人数,先计算出E组人数和A组人数,然后补全频数分布直方图;
(2)用E组的所占百分比乘以360°即可得到在扇形统计图中“E”对应扇形的圆心角的度数;
(3)先画树状图展示所有12种等可能的结果数,找出选出的2人恰好1人选修篮球,1人选修足球所占结果数,然后根据概率公式求解.
本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查条形统计图与扇形统计图.
20.【答案】解:列表得:
???右端
左端 A1B1 B1C1 A1C1
AB AB,A1B1 AB,B1C1 AB,A1C1
BC BC,A1B1 BC,B1C1 BC,A1C1
AC AC,A1B1 AC,B1C1 AC,A1C1
∵分别在两端随机任选两个绳头打结,总共有三类9种情况,每种发生的可能性相等,且能连结成为一根长绳的情况有6种,
①左端连AB,右端连B1C1或A1C1;
②左端连BC,右端连A1B1或A1C1;
③左端连AB,右端连A1B1或B1C1.
∴这三根绳子能连结成一根长绳的概率为:=.
【解析】
首先根据题意列出表格,然后由表格即可求得所有等可能的结果与这三根绳子能连结成一根长绳的情况,再利用概率公式即可求得答案.
此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
21.【答案】解:(1)一共有四个开关按键,只有闭合开关按键K2,灯泡才会发光,
所以P(灯泡发光)=
(2)用树状图分析如下:
一共有12种不同的情况,其中有6种情况下灯泡能发光,
所以P(灯泡发光)=.
【解析】
(1)直接利用概率公式计算得出答案;
(2)利用树状图列举出所有可能,进而求出答案.
本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.
22.【答案】解:(1)袋子中火腿味粽子的个数为2÷=4个;
(2)解:(1)记两个是大枣味的粽子分别为A1,A2,两个火腿味的分别为B1,B2.
树状图如图所示,
由树状图知,一共有12种可能,小丽拿到的两个粽子刚好是同一味道有4种可能,
所以连续2次拿到的两个棕子恰好是同一味道的概率为.
【解析】
(1)用大枣味的数量除以其所占比例即可得.
(2)记两个是大枣味的粽子分别为A1,A2,两个火腿味的分别为B1,B2.画出树状图即可,利用所得的结果,即可解决问题;
本题考查树状图-列表法、概率的求法等知识,记住:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.
23.【答案】3;1
【解析】
解:(1)C类中女生有:20×25%-2=3(名),
D类中男生有20-3-10-5-1=1(人),
条形统计图补充完整如图所示:
(2)根据题意得:(名);
答:九年级女生完成数学作业达到很好和较好的约108人;
(3)根据题意画图如下:
由树状图可得共有6种可能的结果,其中两名同学性别相同的结果有3种,
所以所选两位同学恰好性别相同的概率是.
(1)根据B类有6+4=10人,所占的比例是50%,据此即可求得总人数,再求出C类中女生,D类中男生人数;
(2)求得女生的总人数,然后求得A、B类中女生人数,求出百分比即可解决问题.
(3)利用列举法即可表示出各种情况,然后利用概率公式即可求解.
本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
第2页,共2页
第1页,共1页
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
