3.1 探索勾股定理同步练习(第2课时)
图片预览


文档简介
第三章 勾股定理
1 探索勾股定理
第2课时
新知识记:勾股定理的验证
分类
图形
描述
拼
用两个全等的直角三角形和一个腰长为c的等腰直角三角形拼成一个直角梯形,依据整体面积等于各部分面积之和,可得S梯形= + ,因此有 = + ,化简,得 。
割(补)
把正方形ABCD分割4个直角三角形和一个正方形,则C2=
,即C2= 。
在正方形ABCD的每个边上补上一个边长为a,b,c的直角三角形,得到一个以a+b为边长的正方形,则正方形ABCD的面积C2=
,整理可得C2= 。
典例精析·拓新知
知识点一 勾股定理的证明
【典例1】如图是用硬纸板做成的四个全等的直角三角形,两直角边长分别是a,b,斜边长为c和一个边长为c的正方形,请你将它们拼成一个能证明勾股定理的图形。
(1)画出拼成的这个图形的示意图。
(2)证明勾股定理。
【自主解答】
●学霸提醒
证明勾股定理的三个步骤
(1)读图:观察整个图形是由哪些图形拼接而成,图中括几个直角三角形,几个正方形,它们的边长各是多少。
(2)列式:根据整个图形的面积等于各部分图形的积和,列出关于直角三角形三边长的等式。
(3)化简:根据整式的运算化简等式,得出勾股定理。
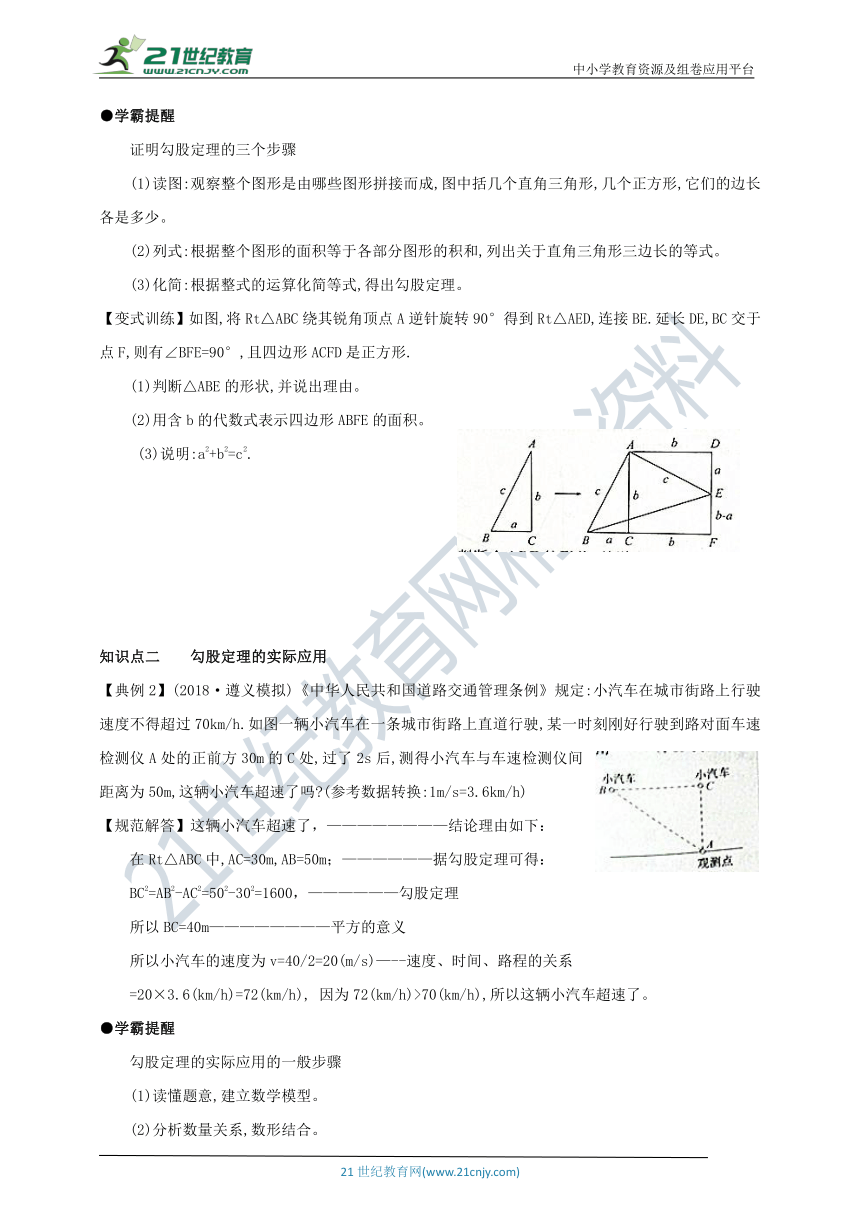
【变式训练】如图,将Rt△ABC绕其锐角顶点A逆针旋转90°得到Rt△AED,连接BE.延长DE,BC交于点F,则有∠BFE=90°,且四边形ACFD是正方形.
(1)判断△ABE的形状,并说出理由。
(2)用含b的代数式表示四边形ABFE的面积。
(3)说明:a2+b2=c2.
知识点二 勾股定理的实际应用
【典例2】(2018·遵义模拟)《中华人民共和国道路交通管理条例》规定:小汽车在城市街路上行驶速度不得超过70km/h.如图一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)
【规范解答】这辆小汽车超速了,————————结论理由如下:
在Rt△ABC中,AC=30m,AB=50m;——————据勾股定理可得:
BC2=AB2-AC2=502-302=1600,——————勾股定理
所以BC=40m————————平方的意义
所以小汽车的速度为v=40/2=20(m/s)—--速度、时间、路程的关系
=20×3.6(km/h)=72(km/h), 因为72(km/h)>70(km/h),所以这辆小汽车超速了。
●学霸提醒
勾股定理的实际应用的一般步骤
(1)读懂题意,建立数学模型。
(2)分析数量关系,数形结合。
(3)应用勾股定理进行计算或建立等量关系,构建方程求解。
(4)解决实际问题
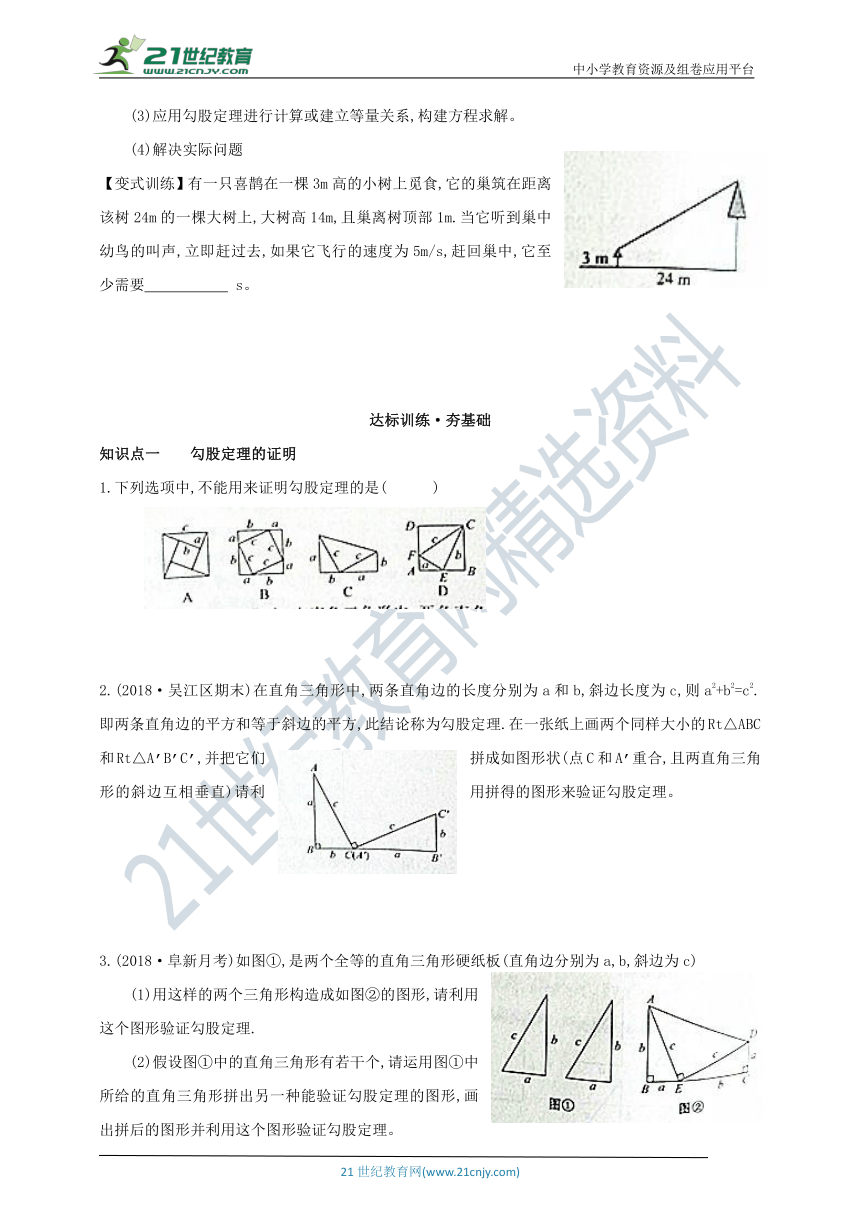
【变式训练】有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m的一棵大树上,大树高14m,且巢离树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,赶回巢中,它至少需要 s。
达标训练·夯基础
知识点一 勾股定理的证明
1.下列选项中,不能用来证明勾股定理的是( )
2.(2018·吴江区期末)在直角三角形中,两条直角边的长度分别为a和b,斜边长度为c,则a2+b2=c2.即两条直角边的平方和等于斜边的平方,此结论称为勾股定理.在一张纸上画两个同样大小的Rt△ABC和Rt△A’B’C’,并把它们拼成如图形状(点C和A’重合,且两直角三角形的斜边互相垂直)请利用拼得的图形来验证勾股定理。
3.(2018·阜新月考)如图①,是两个全等的直角三角形硬纸板(直角边分别为a,b,斜边为c)
(1)用这样的两个三角形构造成如图②的图形,请利用这个图形验证勾股定理.
(2)假设图①中的直角三角形有若干个,请运用图①中所给的直角三角形拼出另一种能验证勾股定理的图形,画出拼后的图形并利用这个图形验证勾股定理。
知识点二 勾股定理的实际应用
1.(2018·诏安模拟)如果梯子的底端离建筑物5m,13m长的梯子可以达到建筑物的高度是( )
A.12m B.13 C.14m D.15
2.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点AB之间的距离是 米。
3.(2018·厦门模拟)已知A,B,C三地位置如图所示,∠C=90°,A,C两地的距离是4km,B,C两地的距离是3km,则A,B两地的距离是 km;若A地在C地的正东方向,则B地在C地的 方向.纠错园
如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长最长可以选用( )
A.3 m B.4 m C.7 D.9 m
解:选A.因为A选项绳长最短,所以用栓羊,羊吃不到菜。
【错因】 。
考题变式·提能力
如图,一棵树在一次强台风中,从离地面3米处折断,量得倒下部分树尖与树根的距离是4米,这棵树在折断前的高度是( )
A.7米 B.8米 C.9米 D.10米
母题变式【变式-】
如图所示,一棵大树高8米,一场大风过后,大树在离地面3米处折断倒下,树的顶端倒在地上,则此时树的顶端离树的底部有 米。( )
A.4 B.3.5 C.5 D.13.6
【变式二】
木工师傅做一个人字形屋梁,如图所示,上弦AB=AC4m,跨度BC为6m,现有一根长为3m的木料打算做中柱AD(AD是△ABC的中线),请你通过计算说明这根木料的长度是否适合做中柱.(只考虑长度,不计损耗)
参考答案及解析
新知识记;
1/2ab×2 1/2C2 1/2(a+b)(a+b)
1/2ab×2 1/2C2 a2+b2=c2 4×1/2ab+(a+b)2
a2+b2 (a+b)2-4×1/2ab a2+b2
典例精析·拓新知
【典例1】【自主解答】方法一(补拼法)
(1)如图(1)所示。
(2)证明:因为大正方形的面积表示为(a+b)2,大正方形的面积也可表示为 c2+4×1/2ab,所以(a+b)2=c2+4×1/2ab,所以a2+b2+2ab=c2+2ab,所以a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方。
方法二(叠合法):(1)如图(2)所示。
(2)证明:因为大正方形的面积可以表示为c2,
也可以表示为1/2ab×4+(b-a)2,
所以c2=1/2 ab×4+(b-a)2,c2=2ab+b2-2ab+a2,
所以a2+b2=c2,即直角三角形两直角边的平方和等于斜边的平方.
【变式训练】解:(1)△ABE是等腰直角三角形。因为Rt△ABC绕其锐角顶点A逆时针旋转90o得到Rt△AED,所以∠BAC=∠DAE,
所以∠BAE=∠BAC+∠CAE=∠CAE+∠DAE=90o,又因为AB=AE,所以△ABE是等腰直角三角形。
(2)因为四边形ABFE的面积等于正方形ACFD的面积,所以四边形ABFE的面积等于b2.
(3)因为S正方形ACFD=S△BAE+S△BFE ,即b2=1/2 c2+1/2 (b+a)(b-a).
整理得2b2=c2+(b+a)(b-a),所以a2+b2=c2.
【典例2】【变式训练】5. 2
达标训练·夯基础
知识点一
1.D
2.解:在直角三角形ABC中,因为∠1+∠2=90o,∠1=∠3,所以∠2+∠3=90o,又因为∠ACC’=90o.
所以∠2+∠3+∠ACC’=180o,所以B,C(A’),B’在同一条直线上,
又∠B=90o,∠B’=90o,所以∠B+∠B’=180°,所以AB∥C’B’,
连接AC’,过点C’作C’D⊥AB交AB于点D,
则四边形ABB’C’面积等于三个直角三角形面积,
所以1/2(a-b)(a+b)+(a+b)b=1/2ab+1/2ab+1/2c2,
即1/2a2-1/2b2+ab+b2=1/2ab+1/2ab+1/2c2,a2+2ab+b2=2ab+c2所以a2+b2=c2
3.解:(1)因为四边形ABCD是梯形,
所以梯形的面积=1/2(a+b)(a+b)=2×1/2×ab+1/2c2,
即1/2(a2+2ab+b2)=ab+1/2c2,所以a2+b2=c2.
(2)如图所示,可以说明a2+ b2=c2
验证:大正方形的面积=4×1/2ab+(b-a)2.大正方形的面积=c2,
所以4×1/2ab+(b-a)2=c2,整理得:a2+b2=c2
知识点二 1.A 2.18 3.5正北
【纠错园】
B 连接OA,交圆于E,在Rt△AOB中,AB=8,OB=6,
由勾股定理得OA=10,所以AE=OA-OE=10-6=4.
考题变式·提能力
B
【母题变式】[变式一]A
[变式二]解:因为AB=AC=4,AD是△ABC的中线,BC=6,所以AD⊥BC,所以BD=1/2BC=3.由勾股定理,得 AD2=AB2-BD2=42-32=7.因为7<32,所以这根木料的长度适合做中柱.
1 探索勾股定理
第2课时
新知识记:勾股定理的验证
分类
图形
描述
拼
用两个全等的直角三角形和一个腰长为c的等腰直角三角形拼成一个直角梯形,依据整体面积等于各部分面积之和,可得S梯形= + ,因此有 = + ,化简,得 。
割(补)
把正方形ABCD分割4个直角三角形和一个正方形,则C2=
,即C2= 。
在正方形ABCD的每个边上补上一个边长为a,b,c的直角三角形,得到一个以a+b为边长的正方形,则正方形ABCD的面积C2=
,整理可得C2= 。
典例精析·拓新知
知识点一 勾股定理的证明
【典例1】如图是用硬纸板做成的四个全等的直角三角形,两直角边长分别是a,b,斜边长为c和一个边长为c的正方形,请你将它们拼成一个能证明勾股定理的图形。
(1)画出拼成的这个图形的示意图。
(2)证明勾股定理。
【自主解答】
●学霸提醒
证明勾股定理的三个步骤
(1)读图:观察整个图形是由哪些图形拼接而成,图中括几个直角三角形,几个正方形,它们的边长各是多少。
(2)列式:根据整个图形的面积等于各部分图形的积和,列出关于直角三角形三边长的等式。
(3)化简:根据整式的运算化简等式,得出勾股定理。
【变式训练】如图,将Rt△ABC绕其锐角顶点A逆针旋转90°得到Rt△AED,连接BE.延长DE,BC交于点F,则有∠BFE=90°,且四边形ACFD是正方形.
(1)判断△ABE的形状,并说出理由。
(2)用含b的代数式表示四边形ABFE的面积。
(3)说明:a2+b2=c2.
知识点二 勾股定理的实际应用
【典例2】(2018·遵义模拟)《中华人民共和国道路交通管理条例》规定:小汽车在城市街路上行驶速度不得超过70km/h.如图一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)
【规范解答】这辆小汽车超速了,————————结论理由如下:
在Rt△ABC中,AC=30m,AB=50m;——————据勾股定理可得:
BC2=AB2-AC2=502-302=1600,——————勾股定理
所以BC=40m————————平方的意义
所以小汽车的速度为v=40/2=20(m/s)—--速度、时间、路程的关系
=20×3.6(km/h)=72(km/h), 因为72(km/h)>70(km/h),所以这辆小汽车超速了。
●学霸提醒
勾股定理的实际应用的一般步骤
(1)读懂题意,建立数学模型。
(2)分析数量关系,数形结合。
(3)应用勾股定理进行计算或建立等量关系,构建方程求解。
(4)解决实际问题
【变式训练】有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m的一棵大树上,大树高14m,且巢离树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,赶回巢中,它至少需要 s。
达标训练·夯基础
知识点一 勾股定理的证明
1.下列选项中,不能用来证明勾股定理的是( )
2.(2018·吴江区期末)在直角三角形中,两条直角边的长度分别为a和b,斜边长度为c,则a2+b2=c2.即两条直角边的平方和等于斜边的平方,此结论称为勾股定理.在一张纸上画两个同样大小的Rt△ABC和Rt△A’B’C’,并把它们拼成如图形状(点C和A’重合,且两直角三角形的斜边互相垂直)请利用拼得的图形来验证勾股定理。
3.(2018·阜新月考)如图①,是两个全等的直角三角形硬纸板(直角边分别为a,b,斜边为c)
(1)用这样的两个三角形构造成如图②的图形,请利用这个图形验证勾股定理.
(2)假设图①中的直角三角形有若干个,请运用图①中所给的直角三角形拼出另一种能验证勾股定理的图形,画出拼后的图形并利用这个图形验证勾股定理。
知识点二 勾股定理的实际应用
1.(2018·诏安模拟)如果梯子的底端离建筑物5m,13m长的梯子可以达到建筑物的高度是( )
A.12m B.13 C.14m D.15
2.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点AB之间的距离是 米。
3.(2018·厦门模拟)已知A,B,C三地位置如图所示,∠C=90°,A,C两地的距离是4km,B,C两地的距离是3km,则A,B两地的距离是 km;若A地在C地的正东方向,则B地在C地的 方向.纠错园
如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长最长可以选用( )
A.3 m B.4 m C.7 D.9 m
解:选A.因为A选项绳长最短,所以用栓羊,羊吃不到菜。
【错因】 。
考题变式·提能力
如图,一棵树在一次强台风中,从离地面3米处折断,量得倒下部分树尖与树根的距离是4米,这棵树在折断前的高度是( )
A.7米 B.8米 C.9米 D.10米
母题变式【变式-】
如图所示,一棵大树高8米,一场大风过后,大树在离地面3米处折断倒下,树的顶端倒在地上,则此时树的顶端离树的底部有 米。( )
A.4 B.3.5 C.5 D.13.6
【变式二】
木工师傅做一个人字形屋梁,如图所示,上弦AB=AC4m,跨度BC为6m,现有一根长为3m的木料打算做中柱AD(AD是△ABC的中线),请你通过计算说明这根木料的长度是否适合做中柱.(只考虑长度,不计损耗)
参考答案及解析
新知识记;
1/2ab×2 1/2C2 1/2(a+b)(a+b)
1/2ab×2 1/2C2 a2+b2=c2 4×1/2ab+(a+b)2
a2+b2 (a+b)2-4×1/2ab a2+b2
典例精析·拓新知
【典例1】【自主解答】方法一(补拼法)
(1)如图(1)所示。
(2)证明:因为大正方形的面积表示为(a+b)2,大正方形的面积也可表示为 c2+4×1/2ab,所以(a+b)2=c2+4×1/2ab,所以a2+b2+2ab=c2+2ab,所以a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方。
方法二(叠合法):(1)如图(2)所示。
(2)证明:因为大正方形的面积可以表示为c2,
也可以表示为1/2ab×4+(b-a)2,
所以c2=1/2 ab×4+(b-a)2,c2=2ab+b2-2ab+a2,
所以a2+b2=c2,即直角三角形两直角边的平方和等于斜边的平方.
【变式训练】解:(1)△ABE是等腰直角三角形。因为Rt△ABC绕其锐角顶点A逆时针旋转90o得到Rt△AED,所以∠BAC=∠DAE,
所以∠BAE=∠BAC+∠CAE=∠CAE+∠DAE=90o,又因为AB=AE,所以△ABE是等腰直角三角形。
(2)因为四边形ABFE的面积等于正方形ACFD的面积,所以四边形ABFE的面积等于b2.
(3)因为S正方形ACFD=S△BAE+S△BFE ,即b2=1/2 c2+1/2 (b+a)(b-a).
整理得2b2=c2+(b+a)(b-a),所以a2+b2=c2.
【典例2】【变式训练】5. 2
达标训练·夯基础
知识点一
1.D
2.解:在直角三角形ABC中,因为∠1+∠2=90o,∠1=∠3,所以∠2+∠3=90o,又因为∠ACC’=90o.
所以∠2+∠3+∠ACC’=180o,所以B,C(A’),B’在同一条直线上,
又∠B=90o,∠B’=90o,所以∠B+∠B’=180°,所以AB∥C’B’,
连接AC’,过点C’作C’D⊥AB交AB于点D,
则四边形ABB’C’面积等于三个直角三角形面积,
所以1/2(a-b)(a+b)+(a+b)b=1/2ab+1/2ab+1/2c2,
即1/2a2-1/2b2+ab+b2=1/2ab+1/2ab+1/2c2,a2+2ab+b2=2ab+c2所以a2+b2=c2
3.解:(1)因为四边形ABCD是梯形,
所以梯形的面积=1/2(a+b)(a+b)=2×1/2×ab+1/2c2,
即1/2(a2+2ab+b2)=ab+1/2c2,所以a2+b2=c2.
(2)如图所示,可以说明a2+ b2=c2
验证:大正方形的面积=4×1/2ab+(b-a)2.大正方形的面积=c2,
所以4×1/2ab+(b-a)2=c2,整理得:a2+b2=c2
知识点二 1.A 2.18 3.5正北
【纠错园】
B 连接OA,交圆于E,在Rt△AOB中,AB=8,OB=6,
由勾股定理得OA=10,所以AE=OA-OE=10-6=4.
考题变式·提能力
B
【母题变式】[变式一]A
[变式二]解:因为AB=AC=4,AD是△ABC的中线,BC=6,所以AD⊥BC,所以BD=1/2BC=3.由勾股定理,得 AD2=AB2-BD2=42-32=7.因为7<32,所以这根木料的长度适合做中柱.
