高中物理课件教科版必修1第3章第5节:牛顿运动定律及其应用
文档属性
| 名称 | 高中物理课件教科版必修1第3章第5节:牛顿运动定律及其应用 |

|
|
| 格式 | rar | ||
| 文件大小 | 926.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2010-11-16 00:00:00 | ||
图片预览










文档简介
课件30张PPT。牛顿运动定律及其应用
牛顿第二定律定律内容(实验方法、表达式)特点:同时性、同向性、同体性应用动力学的两类基本问题同向性问题瞬时性问题力、加速度、速度关系超重与失重力学单位制1.力与运动关系的定性分析例1. 一个物体在几个力作用下处于静止状态,若保持其它力不变,将其中的一个力F1逐渐减小到零(方向保持不变),然后又将F1逐渐恢复原状,在这个过程中物体的( ) A、加速度增大,速度增大 B、加速度减小,速度增大 C、加速度先增大后减小,速度增大 D、加速度和速度都是先增大后减小思考:一小球自由下落,经h高度后落在弹簧上,试分析小球从碰到弹簧开始到弹簧被压缩到最短的过程中,小球位移、速度、加速度的变化规律。
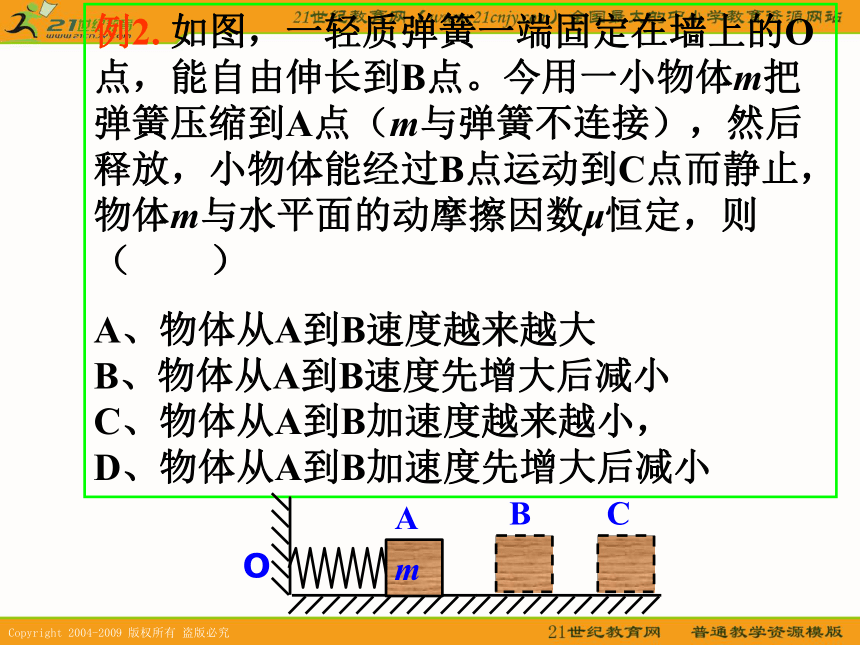
例2. 如图,一轻质弹簧一端固定在墙上的O点,能自由伸长到B点。今用一小物体m把弹簧压缩到A点(m与弹簧不连接),然后释放,小物体能经过B点运动到C点而静止,物体m与水平面的动摩擦因数μ恒定,则( )
A、物体从A到B速度越来越大 B、物体从A到B速度先增大后减小 C、物体从A到B加速度越来越小, D、物体从A到B加速度先增大后减小2.瞬时加速度的分析例3. 如图,在光滑的水平面上,质量分别为m1和m2的木块A和B之间用轻弹簧相连,在拉力F的作用下,以加速度a做匀加速直线运动,某时刻突然撤去拉力F,此瞬时A和B的加速度为a1和a2,则( ) A、a1=a2=0 B、a1=a,a2=0 C、
D、 a1=a,方法总结:确定物体在某一时刻的瞬时加速度,关键在于:1、正确确定该瞬时物体受到的作用力,还要注意
分析物体在这一瞬时前、后的受力及其变化情况。
2、明确两种基本模型的特点。
⑴轻绳不需要形变恢复时间,在瞬时问题中,其
弹力可以突变,成为零或别的值。
⑵轻弹簧(或橡皮绳)需要较长的形变恢复时间,
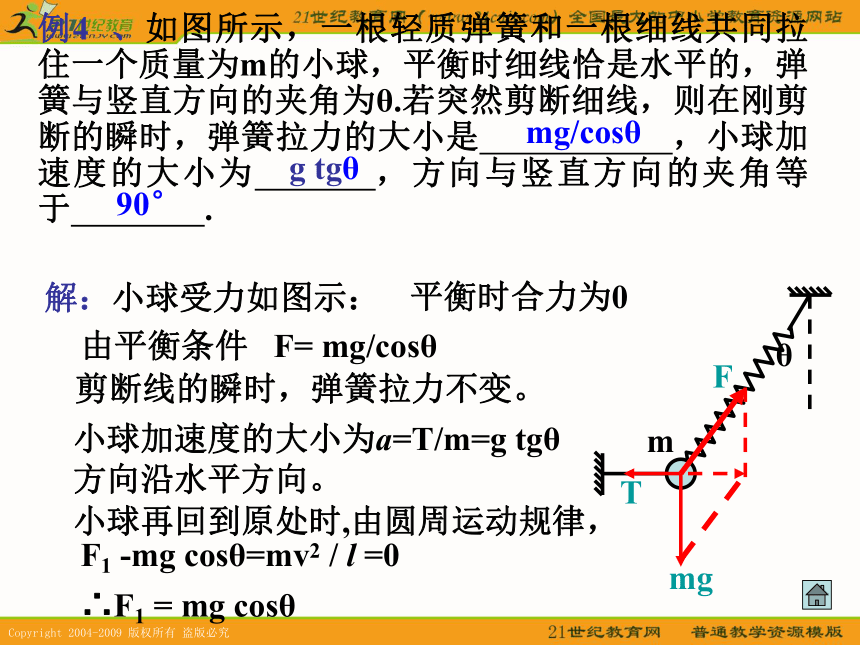
在瞬时间问题中,其弹力不能突变,大小不变。例4 、如图所示,一根轻质弹簧和一根细线共同拉住一个质量为m的小球,平衡时细线恰是水平的,弹簧与竖直方向的夹角为θ.若突然剪断细线,则在刚剪断的瞬时,弹簧拉力的大小是 ,小球加速度的大小为 ,方向与竖直方向的夹角等于 . 解:小球受力如图示: 平衡时合力为0由平衡条件 F= mg/cosθ剪断线的瞬时,弹簧拉力不变。小球加速度的大小为a=T/m=g tgθ
方向沿水平方向。小球再回到原处时,由圆周运动规律,
F1 -mg cosθ=mv2 / l =0∴F1 = mg cosθmg/cosθg tgθ90°2010全国卷.如右图,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态。现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为 、 。重力加速度大小为g。则有 例5 、在运动的升降机中天花板上用细线悬挂一个物体A,下面吊着一个轻质弹簧秤(弹簧秤的质量不计),弹簧秤下吊着物体B,如下图所示,物体A和B的质量相等,都为m=5kg,某一时刻弹簧秤的读数为40N,设g=10 m/s2,则细线的拉力等于_____ ,若将细线剪断,在剪断细线瞬间物体A的加速度是 ,方向 ______ ;
物体B的加速度是 ;
方向 _____ 。 80N18 m/s2向下2 m/s2向下同向性问题分析例6如图所示,在小车中的悬线上挂一个小球,当小车做变速运动时,悬线将不再竖直方向上,则当悬线保持与竖直方向夹角为θ时,小车的加速度是多少?试讨论小车的可能运动情况。 例7质量为m的物体放在倾角为α的斜面上,物体和斜面间的动摩擦系数为μ,如沿水平方向加一个力F,使物体沿斜面向上以加速度a做匀加速直线运动,如下图甲,则F多大?
【例8】如图表示某人站在一架与水平成θ角的以加速度a向上运动的自动扶梯台阶上,人的质量为m,鞋底与阶梯的摩擦系数为μ,求此时人所受的摩擦力. 例9. 一质量为M、倾角为θ的楔形木块,静止在水平桌面上,与桌面的动摩擦因素为μ,一物块质量为m,置于楔形木块的斜面上,物块与斜面的接触是光滑的,为了保持物块相对斜面静止,可用一水平力F推楔形木块,如图示,此水平力的大小等于 。解:对于物块,受力如图示:物块相对斜面静止,只能有向左的加速度,
所以合力一定向左。由牛顿运动定律得mg tg θ=ma a= gtg θ对于整体受力如图示:由牛顿运动定律得F – f = (m+M)aN2 =(m+M)gF = μN2= μ (m+M)g ∴F=f+(m+M)a= (m+M)g(μ +tg θ) (m+M)g(μ+ tgθ)例10、如图,有一斜木块,斜面是光滑的,倾角为θ,放在水平面上,用竖直放置的固定挡板A与斜面夹住一个光滑球,球质量为m,要使球对竖直挡板无压力,球连同斜木块一起应向 (填左、右)做加速运动,加速度大小是 . 解: 画出小球的受力图如图示: 合力一定沿水平方向向左,F=mgtg θ∴a= gtg θ左gtgθ练习、如图示,倾斜索道与水平方向夹角为θ,已知tg θ=3/4,当载人车厢匀加速向上运动时,人对厢底的压力为体重的1.25倍,这时人与车厢相对静止,则车厢对人的摩擦力是体重的 ( )
A. 1/3倍 B.4/3倍
C. 5/4倍 D.1/4倍解:将加速度分解如图示, 由a与合力同向关系,分析人的受力如图示:N-mg=may ay=0.25g f = max = m ay / tg θ
= 0.25mg×4/3 = mg/3 A方法总结:用牛顿第二定律解题时对物体受力的处理方法
1、合成法
2、正交分解法
3、分解加速度法动力学的两类基本问题(1)已知运动求力(2)已知力求运动两类动力学基本问题的解题思路图解如下:07江苏卷 直升机沿水平方向匀速飞往水源取水灭火,悬挂着m=500kg空箱的悬索与竖直方向的夹角θ1=450。直升机取水后飞往火场,加速度沿水平方向,大小稳定在a=1.5 m/s2时,悬索与竖直方向的夹角140。如果空气阻力大小不变,且忽略悬索的质量,谋求水箱中水的质量M。(取重力加速度g=10 m/s2;sin140=0.242;cos 140=0.970)例:如图所示,质量为m = 1㎏的小物块以v0 = 5m/s的初速度滑上一块原来静止在水平面上的木板,木板的质量为M = 4㎏,经过t = 2s后,物块从木板的另一端以v = 1m/s的对地速度滑出,在这一过程中木板的位移为S = 0.5m,求木板与水平面间的动摩擦因素。例:如图示,传送带与水平面夹角为370 ,并以v=10m/s运行,在传送带的A端轻轻放一个小物体,物体与传送带之间的动摩擦因数μ=0.5,AB长16米,求:以下两种情况下物体从A到B所用的时间.
(1)传送带顺时针方向转动
(2)传送带逆时针方向转动解: (1)传送带顺时针方向转动时受力如图示:mg sinθ-μmg cosθ= m aa = gsinθ-μgcosθ= 2m/s2S=1/2at2(2)传送带逆时针方向转动物体受力如图: 开始摩擦力方向向下,向下匀加速运动 a1=g sin370 +μ g cos370 = 10m/s2t1=v/a1=1s S1=1/2 ×a1t12 =5m S2=11m 1秒后,速度达到10m/s,摩擦力方向变为向上 a2=g sin370 -μg cos370 = 2 m/s2 物体以初速度v=10m/s , 向下作匀加速运动 S2= vt2+1/2×a2t22 11=10 t2+1/2×2×t22t2=1s∴t=t1+t2=2s 练习:原地起跳时,先屈腿下蹲,然后突然蹬地。从开始蹬地到离地是加速过程(视为匀加速)加速过程中重心上升的距离称为“加速距离”。离地后重心继续上升,在此过程中重心上升的最大距离称为“竖直高度”。现有下列数据:人原地上跳的“加速距离”,“竖直高度”;跳蚤原地上跳的“加速距离”,“竖直高度”。假想人具有与跳蚤相等的起跳加速度,而“加速距离”仍为0.50m,则人上跳的“竖直高度”是多少?(C05)例2、质量m=2.75t的载重汽车,在F=3000N牵引力的作用下,由静止开始上山坡,当车前进s=100m时速度变为v=26km/h,求该车运动时受到的阻力.(沿山坡每前进1m升高0.05m,g=10 m/s2)(C02) 例3、质量均为m的物体A和B用劲度系数为k的轻弹簧连接在一起,将B放在水平桌面上,A用弹簧支撑着,如图示,若用竖直向上的力拉A,使A以加速度a匀加速上升,试求: (1) 经过多少时间B开始离开桌面
(2) 在B离开桌面之前,拉力的最大值解: (1) 开始时弹簧压缩 x=mg/k B开始离开桌面时,弹簧伸长 x=mg/k A匀加速上升了 S=2x=2 mg/k 由匀加速运动公式(2) 在B离开桌面之前, 对A物体: F-mg-T=ma当T=mg时B离开桌面∴Fmax =2mg+ma例:如图示:竖直放置的弹簧下端固定,上端连接一个砝码盘B,盘中放一个物体A,A、 B的质量分别是M=10.5kg、m=1.5 kg,k=800N/m,对A施加一个竖直向上的拉力,使它做匀加速直线运动,经过0.2秒A与B脱离,刚脱离时刻的速度为v=1.2m/s,取g=10m/s2,求A在运动过程中拉力的最大值与最小值。解:对整体 kx1=(M+m)g F + kx - (M+m)g= (M+m)a脱离时,A 、B间无相互作 用力,
对B kx2-mg=max1- x2 =1/2 at2 a=v/t=6m/s2Fmax=Mg+Ma=168NFmin=(M+m)a=72N 例、如图示, 倾角30°的光滑斜面上,并排放着质量分别是mA=10kg和mB=2kg的A、B两物块,一个劲度系数k=400N/m的轻弹簧一端与物块B相连,另一端与固定挡板相连,整个系统处于静止状态,现对A施加一沿斜面向上的力F,使物块A沿斜面向上作匀加速运动,已知力 F在前0.2s内为变力,0.2s后为恒力,g取10m/s2 , 求F的最大值和最小值。解:开始静止时弹簧压缩 x1=(m1 +m2)g sinα/ k = 0.15m 0.2s 末A、B即将分离, A、B间无作用力,对B物块:kx2-m2g sinα = m2a ⑴x1-x2=1/2at2 ⑵ 解得 x2=0.05m a=5 m/s2 t=0时,F最小,对AB整体 Fmin = (m1 + m2) a = 60Nt=0.2s 时,F最大,对A物块:Fmax - m1g sinα = m1aFmax = m1g sinα + m1a = 100N
牛顿第二定律定律内容(实验方法、表达式)特点:同时性、同向性、同体性应用动力学的两类基本问题同向性问题瞬时性问题力、加速度、速度关系超重与失重力学单位制1.力与运动关系的定性分析例1. 一个物体在几个力作用下处于静止状态,若保持其它力不变,将其中的一个力F1逐渐减小到零(方向保持不变),然后又将F1逐渐恢复原状,在这个过程中物体的( ) A、加速度增大,速度增大 B、加速度减小,速度增大 C、加速度先增大后减小,速度增大 D、加速度和速度都是先增大后减小思考:一小球自由下落,经h高度后落在弹簧上,试分析小球从碰到弹簧开始到弹簧被压缩到最短的过程中,小球位移、速度、加速度的变化规律。
例2. 如图,一轻质弹簧一端固定在墙上的O点,能自由伸长到B点。今用一小物体m把弹簧压缩到A点(m与弹簧不连接),然后释放,小物体能经过B点运动到C点而静止,物体m与水平面的动摩擦因数μ恒定,则( )
A、物体从A到B速度越来越大 B、物体从A到B速度先增大后减小 C、物体从A到B加速度越来越小, D、物体从A到B加速度先增大后减小2.瞬时加速度的分析例3. 如图,在光滑的水平面上,质量分别为m1和m2的木块A和B之间用轻弹簧相连,在拉力F的作用下,以加速度a做匀加速直线运动,某时刻突然撤去拉力F,此瞬时A和B的加速度为a1和a2,则( ) A、a1=a2=0 B、a1=a,a2=0 C、
D、 a1=a,方法总结:确定物体在某一时刻的瞬时加速度,关键在于:1、正确确定该瞬时物体受到的作用力,还要注意
分析物体在这一瞬时前、后的受力及其变化情况。
2、明确两种基本模型的特点。
⑴轻绳不需要形变恢复时间,在瞬时问题中,其
弹力可以突变,成为零或别的值。
⑵轻弹簧(或橡皮绳)需要较长的形变恢复时间,
在瞬时间问题中,其弹力不能突变,大小不变。例4 、如图所示,一根轻质弹簧和一根细线共同拉住一个质量为m的小球,平衡时细线恰是水平的,弹簧与竖直方向的夹角为θ.若突然剪断细线,则在刚剪断的瞬时,弹簧拉力的大小是 ,小球加速度的大小为 ,方向与竖直方向的夹角等于 . 解:小球受力如图示: 平衡时合力为0由平衡条件 F= mg/cosθ剪断线的瞬时,弹簧拉力不变。小球加速度的大小为a=T/m=g tgθ
方向沿水平方向。小球再回到原处时,由圆周运动规律,
F1 -mg cosθ=mv2 / l =0∴F1 = mg cosθmg/cosθg tgθ90°2010全国卷.如右图,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态。现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为 、 。重力加速度大小为g。则有 例5 、在运动的升降机中天花板上用细线悬挂一个物体A,下面吊着一个轻质弹簧秤(弹簧秤的质量不计),弹簧秤下吊着物体B,如下图所示,物体A和B的质量相等,都为m=5kg,某一时刻弹簧秤的读数为40N,设g=10 m/s2,则细线的拉力等于_____ ,若将细线剪断,在剪断细线瞬间物体A的加速度是 ,方向 ______ ;
物体B的加速度是 ;
方向 _____ 。 80N18 m/s2向下2 m/s2向下同向性问题分析例6如图所示,在小车中的悬线上挂一个小球,当小车做变速运动时,悬线将不再竖直方向上,则当悬线保持与竖直方向夹角为θ时,小车的加速度是多少?试讨论小车的可能运动情况。 例7质量为m的物体放在倾角为α的斜面上,物体和斜面间的动摩擦系数为μ,如沿水平方向加一个力F,使物体沿斜面向上以加速度a做匀加速直线运动,如下图甲,则F多大?
【例8】如图表示某人站在一架与水平成θ角的以加速度a向上运动的自动扶梯台阶上,人的质量为m,鞋底与阶梯的摩擦系数为μ,求此时人所受的摩擦力. 例9. 一质量为M、倾角为θ的楔形木块,静止在水平桌面上,与桌面的动摩擦因素为μ,一物块质量为m,置于楔形木块的斜面上,物块与斜面的接触是光滑的,为了保持物块相对斜面静止,可用一水平力F推楔形木块,如图示,此水平力的大小等于 。解:对于物块,受力如图示:物块相对斜面静止,只能有向左的加速度,
所以合力一定向左。由牛顿运动定律得mg tg θ=ma a= gtg θ对于整体受力如图示:由牛顿运动定律得F – f = (m+M)aN2 =(m+M)gF = μN2= μ (m+M)g ∴F=f+(m+M)a= (m+M)g(μ +tg θ) (m+M)g(μ+ tgθ)例10、如图,有一斜木块,斜面是光滑的,倾角为θ,放在水平面上,用竖直放置的固定挡板A与斜面夹住一个光滑球,球质量为m,要使球对竖直挡板无压力,球连同斜木块一起应向 (填左、右)做加速运动,加速度大小是 . 解: 画出小球的受力图如图示: 合力一定沿水平方向向左,F=mgtg θ∴a= gtg θ左gtgθ练习、如图示,倾斜索道与水平方向夹角为θ,已知tg θ=3/4,当载人车厢匀加速向上运动时,人对厢底的压力为体重的1.25倍,这时人与车厢相对静止,则车厢对人的摩擦力是体重的 ( )
A. 1/3倍 B.4/3倍
C. 5/4倍 D.1/4倍解:将加速度分解如图示, 由a与合力同向关系,分析人的受力如图示:N-mg=may ay=0.25g f = max = m ay / tg θ
= 0.25mg×4/3 = mg/3 A方法总结:用牛顿第二定律解题时对物体受力的处理方法
1、合成法
2、正交分解法
3、分解加速度法动力学的两类基本问题(1)已知运动求力(2)已知力求运动两类动力学基本问题的解题思路图解如下:07江苏卷 直升机沿水平方向匀速飞往水源取水灭火,悬挂着m=500kg空箱的悬索与竖直方向的夹角θ1=450。直升机取水后飞往火场,加速度沿水平方向,大小稳定在a=1.5 m/s2时,悬索与竖直方向的夹角140。如果空气阻力大小不变,且忽略悬索的质量,谋求水箱中水的质量M。(取重力加速度g=10 m/s2;sin140=0.242;cos 140=0.970)例:如图所示,质量为m = 1㎏的小物块以v0 = 5m/s的初速度滑上一块原来静止在水平面上的木板,木板的质量为M = 4㎏,经过t = 2s后,物块从木板的另一端以v = 1m/s的对地速度滑出,在这一过程中木板的位移为S = 0.5m,求木板与水平面间的动摩擦因素。例:如图示,传送带与水平面夹角为370 ,并以v=10m/s运行,在传送带的A端轻轻放一个小物体,物体与传送带之间的动摩擦因数μ=0.5,AB长16米,求:以下两种情况下物体从A到B所用的时间.
(1)传送带顺时针方向转动
(2)传送带逆时针方向转动解: (1)传送带顺时针方向转动时受力如图示:mg sinθ-μmg cosθ= m aa = gsinθ-μgcosθ= 2m/s2S=1/2at2(2)传送带逆时针方向转动物体受力如图: 开始摩擦力方向向下,向下匀加速运动 a1=g sin370 +μ g cos370 = 10m/s2t1=v/a1=1s S1=1/2 ×a1t12 =5m S2=11m 1秒后,速度达到10m/s,摩擦力方向变为向上 a2=g sin370 -μg cos370 = 2 m/s2 物体以初速度v=10m/s , 向下作匀加速运动 S2= vt2+1/2×a2t22 11=10 t2+1/2×2×t22t2=1s∴t=t1+t2=2s 练习:原地起跳时,先屈腿下蹲,然后突然蹬地。从开始蹬地到离地是加速过程(视为匀加速)加速过程中重心上升的距离称为“加速距离”。离地后重心继续上升,在此过程中重心上升的最大距离称为“竖直高度”。现有下列数据:人原地上跳的“加速距离”,“竖直高度”;跳蚤原地上跳的“加速距离”,“竖直高度”。假想人具有与跳蚤相等的起跳加速度,而“加速距离”仍为0.50m,则人上跳的“竖直高度”是多少?(C05)例2、质量m=2.75t的载重汽车,在F=3000N牵引力的作用下,由静止开始上山坡,当车前进s=100m时速度变为v=26km/h,求该车运动时受到的阻力.(沿山坡每前进1m升高0.05m,g=10 m/s2)(C02) 例3、质量均为m的物体A和B用劲度系数为k的轻弹簧连接在一起,将B放在水平桌面上,A用弹簧支撑着,如图示,若用竖直向上的力拉A,使A以加速度a匀加速上升,试求: (1) 经过多少时间B开始离开桌面
(2) 在B离开桌面之前,拉力的最大值解: (1) 开始时弹簧压缩 x=mg/k B开始离开桌面时,弹簧伸长 x=mg/k A匀加速上升了 S=2x=2 mg/k 由匀加速运动公式(2) 在B离开桌面之前, 对A物体: F-mg-T=ma当T=mg时B离开桌面∴Fmax =2mg+ma例:如图示:竖直放置的弹簧下端固定,上端连接一个砝码盘B,盘中放一个物体A,A、 B的质量分别是M=10.5kg、m=1.5 kg,k=800N/m,对A施加一个竖直向上的拉力,使它做匀加速直线运动,经过0.2秒A与B脱离,刚脱离时刻的速度为v=1.2m/s,取g=10m/s2,求A在运动过程中拉力的最大值与最小值。解:对整体 kx1=(M+m)g F + kx - (M+m)g= (M+m)a脱离时,A 、B间无相互作 用力,
对B kx2-mg=max1- x2 =1/2 at2 a=v/t=6m/s2Fmax=Mg+Ma=168NFmin=(M+m)a=72N 例、如图示, 倾角30°的光滑斜面上,并排放着质量分别是mA=10kg和mB=2kg的A、B两物块,一个劲度系数k=400N/m的轻弹簧一端与物块B相连,另一端与固定挡板相连,整个系统处于静止状态,现对A施加一沿斜面向上的力F,使物块A沿斜面向上作匀加速运动,已知力 F在前0.2s内为变力,0.2s后为恒力,g取10m/s2 , 求F的最大值和最小值。解:开始静止时弹簧压缩 x1=(m1 +m2)g sinα/ k = 0.15m 0.2s 末A、B即将分离, A、B间无作用力,对B物块:kx2-m2g sinα = m2a ⑴x1-x2=1/2at2 ⑵ 解得 x2=0.05m a=5 m/s2 t=0时,F最小,对AB整体 Fmin = (m1 + m2) a = 60Nt=0.2s 时,F最大,对A物块:Fmax - m1g sinα = m1aFmax = m1g sinα + m1a = 100N
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
