第三章相互作用3.4力的合成课件1:48张PPT
文档属性
| 名称 | 第三章相互作用3.4力的合成课件1:48张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-10-03 21:57:47 | ||
图片预览











文档简介
课件48张PPT。4
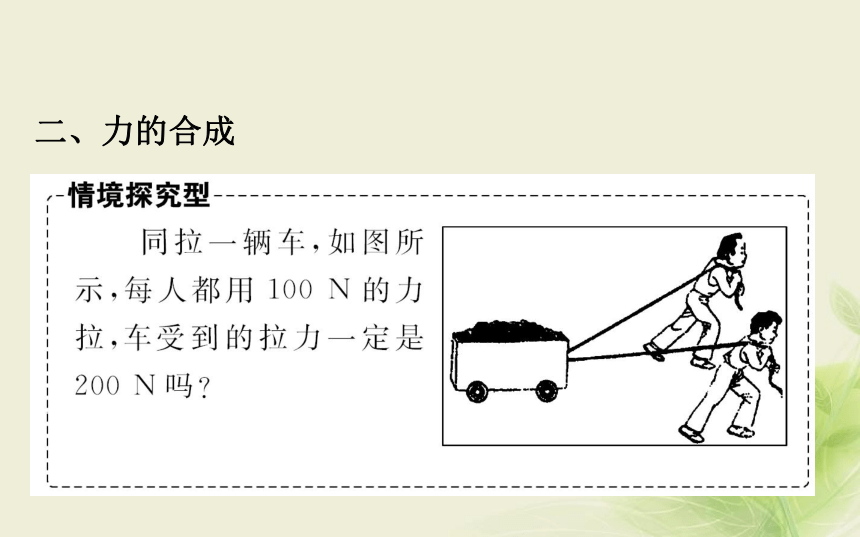
力 的 合 成 一、合力与分力
当一个物体受到几个力的共同作用时,我们常常可以求
出这样一个力,这个力产生的_____跟原来几个力的共同
效果相同,这个力就叫作那几个力的_____,原来的几个
力叫作_____。效果合力分力二、力的合成1.定义:求_____________的过程叫作力的合成。
2.平行四边形定则:两个力合成时,以表示这两个力的
有向线段为_____作平行四边形,这两个邻边之间的
_______就代表合力的大小和方向。
如图所示,__表示F1与F2的合力。几个力的合力邻边对角线F3.多力合成的方法:先求出___________的合力,再求出
这个合力与_________的合力,直到把所有的力都合成
进去,最后得到的结果就是这些力的合力。任意两个力第三个力三、共点力
1.定义:作用在物体的_________或者延长线_________
的一组力。
2.力的合成适用范围:力的合成遵从平行四边形定则,
只适用于_______。同一点上交于一点共点力【思考辨析】
(1)合力与分力同时作用在一个物体上。 ( )
(2)由作出的力的平行四边形定则可知,合力可能小于分力。 ( )
(3)共点力一定作用于物体上的同一点。 ( )(4)作用于同一物体上的所有的力都是共点力。 ( )
(5)作用于不同物体上的两个力,只要作用线交于一点,就可以进行力的合成。 ( )
提示:(1)×。合力与分力是等效替代关系,不会同时作用在一个物体上。
(2)√。由作出的力的平行四边形定则可以看出,对角线可能比平行四边形的边长长,也可能短,即合力可能大于分力,也可能小于分力,甚至等于分力。
(3)×。共点力不一定作用于物体上的同一点,也可能是共点力的作用线交于一点。(4)×。共点力一定作用于同一物体上,但作用于同一物体上的力不一定是共点力,如作用于同一物体上的平行力就不一定是共点力。
(5)×。共点力必须是作用在同一个物体上的力,而只有共点力才能进行力的合成。
一 合力与分力的关系
【典例】两个力F1和F2间的夹角为θ,两个力的合力为F。以下说法正确的是 导学号28974076( )
A.若F1和F2大小不变,θ角越小,合力F就越小
B.合力F可能比任何一个分力都小C.合力F总比任何一个分力都大
D.如果夹角θ不变,F1大小不变,只要F2增大,合力F就必然增大
【正确解答】选B。若F1和F2大小不变,θ角越小,合力F越大,故A错误;由力的合成方法可知,两个力合力的范围|F1-F2|≤F≤F1+F2,所以合力有可能大于任一分力,也可能小于任一分力,还可能与两个分力都相等,故B正确,C错误;如果夹角θ不变,F1大小不变,F2增大,合力可能增大,可能减小,如图所示,故D错误。【核心归纳】
1.合力与分力的三个性质:2.合力与分力的大小关系:
两分力大小不变时,合力F随两分力夹角θ的增大而减小,随θ的减小而增大。
(1)两分力同向(θ=0°)时,合力最大,F=F1+F2,合力与分力同向。(2)两分力反向(θ=180°)时,合力最小,F=|F1-F2|,合力的方向与较大的一个分力的方向相同。
(3)合力的取值范围:|F1-F2|≤F≤F1+F2。
【特别提醒】(1)两分力同向(或反向)时F=F1+F2(F=|F1-F2|),可看作平行四边形定则在θ=0°(和θ=180°)时的特例。
(2)合力可以比两个分力都大,可以比两个分力都小,也可以介于两个分力之间或者与其中一个分力相等。【过关训练】
如图所示,为两个共点力的合力F随两分力的夹角θ变化的图象,则这两个分力的大小分别为 ( )
A.1 N和4 N
B.2 N和3 N
C.1 N和5 N
D.2 N和4 N【解析】选B。两个分力之和为最大值,两个分力之差为最小值,即F1+F2=5 N,F1-F2=1 N。解得F1=3 N,F2=
2 N,B正确。【补偿训练】
1.如图所示,有两个共点力,一个是F1=40 N,一个是F2,它们的合力是F=100 N,则F2的大小可能是 ( )
A.20 N
B.40 N
C.80 N
D.160 N【解析】选C。两个共点力的合力大小的取值范围是|F1-F2|≤F≤F1+F2。根据以上关系,可以求得F2大小的取值范围是60 N≤F2≤140 N,故只有选项C正确。2.同时作用在某物体上的两个方向相反的力,大小分别为8 N和10 N,在10 N的力逐步减小到零的过程中,两个力的合力的大小 ( )
A.先减小后增大 B.先增大后减小
C.一直减小 D.一直增大【解析】选A。当10 N的力减小到8 N时,两力的合力最小为0,原10 N的力再减小,两力的合力又将逐渐增大,减小到零时,两力的合力最大为8 N,故A正确。二 求合力的方法
考查角度1 作图法求合力
【典例1】(2018·德州高一检测)2018年1月1日通车的
港珠澳大桥是一座跨海大桥,连接香港大屿山、澳门半
岛和广东省珠海市,全长为49.968公里,主体工程“海
中桥隧”长35.578公里,其中海底隧道长约6.75公里,桥梁长约29公里。桥梁采用斜拉索式,如图假设斜拉桥中对钢索与竖直方向的夹角都是30°,每根钢索中的拉力都是3×104 N,那么它们对塔柱形成的合力有多大?方向如何? 导学号28974077
【正确解答】把两根钢索的拉力看成
沿钢索方向的两个分力,以它们为邻
边画出一个平行四边形,其对角线就
表示它们的合力。由对称性可知,合
力方向一定沿塔柱竖直向下。下面用作图法求这个合力的大小:自O点引两根有向线段OA和OB,它们跟竖直方向的夹角都为30°。取单位长度为1×104 N,则OA和OB的长度都是3个单位长度。量得对角线OC长为5.2个单位长度,所以合力的大小为F=5.2×1×104 N=5.2×
104 N。
答案:5.2×104 N 竖直向下
【核心归纳】
作图法求合力的步骤【特别提醒】作图法求合力注意的问题
(1)作图时要先确定力的标度,同一图上的各个力必须采用同一标度。
(2)严格采用作图工具作图,并用测量工具测出力的大小及方向。
(3)作图时表示分力和合力的有向线段要画成实线,与分力平行的对边要画成虚线,表示力的线段上要画上刻度和箭头。考查角度2 计算法求合力
【典例2】如图所示,水平横梁一端A插在墙壁内,另一端装有一小滑轮B。一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量为m=10 kg的重物,∠CBA =30°,则滑轮受到绳子的作用力大小为(g取10 N/kg) 导学号28974078( )A.50 N
B.60 N
C.120 N
D.100 N【正确解答】选D。轻绳跨过滑轮,
BC段、BD段拉力F1=F2=mg=100 N,
夹角为120°,根据平行四边形定
则,二力合成如图所示。由于F1=F2,所以平行四边形为菱形,又因为∠DBG=60°,所以△BGD为等边三角形,所以F1、F2的合力F=F1=F2=100 N,即绳子对滑轮的作用力大小为100 N,选项D正确。【核心归纳】
1.计算法:
(1)可先根据平行四边形定则做出分力及合力的示意图。
(2)根据几何知识求解对角线,即为合力。2.两种特殊情况下合力的计算
【特别提醒】计算法求合力时常用到的几何知识
(1)应用直角三角形中的边角关系求解。
(2)应用等边三角形的特点求解。
(3)应用相似三角形的知识求解。【过关训练】
(2018·龙岩高一检测)如图所示,
两个人共同用力将一个牌匾拉上
墙头。其中一人用了450 N的拉
力,另一个人用了600 N的拉力,如果这两个人所用拉力的夹角是90°,求它们的合力。(试用两种方法求合力) 导学号28974079【解析】解法一:作图法
如图所示,用图示中的线段表示150 N
的力,用一个点O代表牌匾,依题意作
出力的平行四边形。用刻度尺量出平
行四边形的对角线长为图示线段的5倍,故合力大小为F=150×5 N=750 N,用量角器量出合力F与F1的夹角θ=53°。解法二:计算法
设F1=450 N,F2=600 N,合力为F。
由于F1与F2间的夹角为90°,根据勾股定理,得
F= =750 N,
合力F与F1的夹角θ的正切tan θ= ≈1.33,
所以θ=53°。
答案:750 N,方向与较小拉力的夹角为53°。【补偿训练】
物体受两个大小都等于10 N的拉力作用,且这两个拉力间的夹角为90°,求这两个力的合力的大小和方向。【解析】方法一(作图法):选取1 cm表示5 N,作出两个力的图示,再以这两力的图示为邻边作平行四边形,如图所示。用刻度尺量出对角线的长度约为2.8 cm,
则合力大小为F= ×5 N=14.0 N。
用量角器测出合力F的方向与F1夹角为45°。
方法二(计算法):作出力的合成的平行四边形示意图
如图所示。则该平行四边形为正方形,由几何知识得合力
F= F1=10 N≈14.0 N,
合力F的方向与F1夹角为45°。
答案:14.0 N 方向与F1夹角为45° 【拓展例题】考查内容:多力合成
【典例】如图所示,在同一平面内,大小分别为1 N、
2 N、3 N、4 N、5 N、6 N的六个力共同作用于一点,其合力大小为 ( )
A.0 B.1 N
C.2 N D.3 N【正确解答】选A。先分别求1 N和4 N、2 N和5 N、
3 N和6 N的合力,大小都为3 N,且三个合力互成120°角,如图所示:根据平行四边形定则知,图中三个力的合力为零,即题中所给六个力的最终合力为零。故A正确,B、C、D错误。
力 的 合 成 一、合力与分力
当一个物体受到几个力的共同作用时,我们常常可以求
出这样一个力,这个力产生的_____跟原来几个力的共同
效果相同,这个力就叫作那几个力的_____,原来的几个
力叫作_____。效果合力分力二、力的合成1.定义:求_____________的过程叫作力的合成。
2.平行四边形定则:两个力合成时,以表示这两个力的
有向线段为_____作平行四边形,这两个邻边之间的
_______就代表合力的大小和方向。
如图所示,__表示F1与F2的合力。几个力的合力邻边对角线F3.多力合成的方法:先求出___________的合力,再求出
这个合力与_________的合力,直到把所有的力都合成
进去,最后得到的结果就是这些力的合力。任意两个力第三个力三、共点力
1.定义:作用在物体的_________或者延长线_________
的一组力。
2.力的合成适用范围:力的合成遵从平行四边形定则,
只适用于_______。同一点上交于一点共点力【思考辨析】
(1)合力与分力同时作用在一个物体上。 ( )
(2)由作出的力的平行四边形定则可知,合力可能小于分力。 ( )
(3)共点力一定作用于物体上的同一点。 ( )(4)作用于同一物体上的所有的力都是共点力。 ( )
(5)作用于不同物体上的两个力,只要作用线交于一点,就可以进行力的合成。 ( )
提示:(1)×。合力与分力是等效替代关系,不会同时作用在一个物体上。
(2)√。由作出的力的平行四边形定则可以看出,对角线可能比平行四边形的边长长,也可能短,即合力可能大于分力,也可能小于分力,甚至等于分力。
(3)×。共点力不一定作用于物体上的同一点,也可能是共点力的作用线交于一点。(4)×。共点力一定作用于同一物体上,但作用于同一物体上的力不一定是共点力,如作用于同一物体上的平行力就不一定是共点力。
(5)×。共点力必须是作用在同一个物体上的力,而只有共点力才能进行力的合成。
一 合力与分力的关系
【典例】两个力F1和F2间的夹角为θ,两个力的合力为F。以下说法正确的是 导学号28974076( )
A.若F1和F2大小不变,θ角越小,合力F就越小
B.合力F可能比任何一个分力都小C.合力F总比任何一个分力都大
D.如果夹角θ不变,F1大小不变,只要F2增大,合力F就必然增大
【正确解答】选B。若F1和F2大小不变,θ角越小,合力F越大,故A错误;由力的合成方法可知,两个力合力的范围|F1-F2|≤F≤F1+F2,所以合力有可能大于任一分力,也可能小于任一分力,还可能与两个分力都相等,故B正确,C错误;如果夹角θ不变,F1大小不变,F2增大,合力可能增大,可能减小,如图所示,故D错误。【核心归纳】
1.合力与分力的三个性质:2.合力与分力的大小关系:
两分力大小不变时,合力F随两分力夹角θ的增大而减小,随θ的减小而增大。
(1)两分力同向(θ=0°)时,合力最大,F=F1+F2,合力与分力同向。(2)两分力反向(θ=180°)时,合力最小,F=|F1-F2|,合力的方向与较大的一个分力的方向相同。
(3)合力的取值范围:|F1-F2|≤F≤F1+F2。
【特别提醒】(1)两分力同向(或反向)时F=F1+F2(F=|F1-F2|),可看作平行四边形定则在θ=0°(和θ=180°)时的特例。
(2)合力可以比两个分力都大,可以比两个分力都小,也可以介于两个分力之间或者与其中一个分力相等。【过关训练】
如图所示,为两个共点力的合力F随两分力的夹角θ变化的图象,则这两个分力的大小分别为 ( )
A.1 N和4 N
B.2 N和3 N
C.1 N和5 N
D.2 N和4 N【解析】选B。两个分力之和为最大值,两个分力之差为最小值,即F1+F2=5 N,F1-F2=1 N。解得F1=3 N,F2=
2 N,B正确。【补偿训练】
1.如图所示,有两个共点力,一个是F1=40 N,一个是F2,它们的合力是F=100 N,则F2的大小可能是 ( )
A.20 N
B.40 N
C.80 N
D.160 N【解析】选C。两个共点力的合力大小的取值范围是|F1-F2|≤F≤F1+F2。根据以上关系,可以求得F2大小的取值范围是60 N≤F2≤140 N,故只有选项C正确。2.同时作用在某物体上的两个方向相反的力,大小分别为8 N和10 N,在10 N的力逐步减小到零的过程中,两个力的合力的大小 ( )
A.先减小后增大 B.先增大后减小
C.一直减小 D.一直增大【解析】选A。当10 N的力减小到8 N时,两力的合力最小为0,原10 N的力再减小,两力的合力又将逐渐增大,减小到零时,两力的合力最大为8 N,故A正确。二 求合力的方法
考查角度1 作图法求合力
【典例1】(2018·德州高一检测)2018年1月1日通车的
港珠澳大桥是一座跨海大桥,连接香港大屿山、澳门半
岛和广东省珠海市,全长为49.968公里,主体工程“海
中桥隧”长35.578公里,其中海底隧道长约6.75公里,桥梁长约29公里。桥梁采用斜拉索式,如图假设斜拉桥中对钢索与竖直方向的夹角都是30°,每根钢索中的拉力都是3×104 N,那么它们对塔柱形成的合力有多大?方向如何? 导学号28974077
【正确解答】把两根钢索的拉力看成
沿钢索方向的两个分力,以它们为邻
边画出一个平行四边形,其对角线就
表示它们的合力。由对称性可知,合
力方向一定沿塔柱竖直向下。下面用作图法求这个合力的大小:自O点引两根有向线段OA和OB,它们跟竖直方向的夹角都为30°。取单位长度为1×104 N,则OA和OB的长度都是3个单位长度。量得对角线OC长为5.2个单位长度,所以合力的大小为F=5.2×1×104 N=5.2×
104 N。
答案:5.2×104 N 竖直向下
【核心归纳】
作图法求合力的步骤【特别提醒】作图法求合力注意的问题
(1)作图时要先确定力的标度,同一图上的各个力必须采用同一标度。
(2)严格采用作图工具作图,并用测量工具测出力的大小及方向。
(3)作图时表示分力和合力的有向线段要画成实线,与分力平行的对边要画成虚线,表示力的线段上要画上刻度和箭头。考查角度2 计算法求合力
【典例2】如图所示,水平横梁一端A插在墙壁内,另一端装有一小滑轮B。一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量为m=10 kg的重物,∠CBA =30°,则滑轮受到绳子的作用力大小为(g取10 N/kg) 导学号28974078( )A.50 N
B.60 N
C.120 N
D.100 N【正确解答】选D。轻绳跨过滑轮,
BC段、BD段拉力F1=F2=mg=100 N,
夹角为120°,根据平行四边形定
则,二力合成如图所示。由于F1=F2,所以平行四边形为菱形,又因为∠DBG=60°,所以△BGD为等边三角形,所以F1、F2的合力F=F1=F2=100 N,即绳子对滑轮的作用力大小为100 N,选项D正确。【核心归纳】
1.计算法:
(1)可先根据平行四边形定则做出分力及合力的示意图。
(2)根据几何知识求解对角线,即为合力。2.两种特殊情况下合力的计算
【特别提醒】计算法求合力时常用到的几何知识
(1)应用直角三角形中的边角关系求解。
(2)应用等边三角形的特点求解。
(3)应用相似三角形的知识求解。【过关训练】
(2018·龙岩高一检测)如图所示,
两个人共同用力将一个牌匾拉上
墙头。其中一人用了450 N的拉
力,另一个人用了600 N的拉力,如果这两个人所用拉力的夹角是90°,求它们的合力。(试用两种方法求合力) 导学号28974079【解析】解法一:作图法
如图所示,用图示中的线段表示150 N
的力,用一个点O代表牌匾,依题意作
出力的平行四边形。用刻度尺量出平
行四边形的对角线长为图示线段的5倍,故合力大小为F=150×5 N=750 N,用量角器量出合力F与F1的夹角θ=53°。解法二:计算法
设F1=450 N,F2=600 N,合力为F。
由于F1与F2间的夹角为90°,根据勾股定理,得
F= =750 N,
合力F与F1的夹角θ的正切tan θ= ≈1.33,
所以θ=53°。
答案:750 N,方向与较小拉力的夹角为53°。【补偿训练】
物体受两个大小都等于10 N的拉力作用,且这两个拉力间的夹角为90°,求这两个力的合力的大小和方向。【解析】方法一(作图法):选取1 cm表示5 N,作出两个力的图示,再以这两力的图示为邻边作平行四边形,如图所示。用刻度尺量出对角线的长度约为2.8 cm,
则合力大小为F= ×5 N=14.0 N。
用量角器测出合力F的方向与F1夹角为45°。
方法二(计算法):作出力的合成的平行四边形示意图
如图所示。则该平行四边形为正方形,由几何知识得合力
F= F1=10 N≈14.0 N,
合力F的方向与F1夹角为45°。
答案:14.0 N 方向与F1夹角为45° 【拓展例题】考查内容:多力合成
【典例】如图所示,在同一平面内,大小分别为1 N、
2 N、3 N、4 N、5 N、6 N的六个力共同作用于一点,其合力大小为 ( )
A.0 B.1 N
C.2 N D.3 N【正确解答】选A。先分别求1 N和4 N、2 N和5 N、
3 N和6 N的合力,大小都为3 N,且三个合力互成120°角,如图所示:根据平行四边形定则知,图中三个力的合力为零,即题中所给六个力的最终合力为零。故A正确,B、C、D错误。
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
