第四章牛顿运动定律4.6用牛顿运动定律解决问题(一)课件2:75张PPT
文档属性
| 名称 | 第四章牛顿运动定律4.6用牛顿运动定律解决问题(一)课件2:75张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-10-03 22:21:44 | ||
图片预览











文档简介
课件75张PPT。6
用牛顿运动定律解决问题(一)一、牛顿第二定律的作用
确定了_________的关系,把物体的运动情况与
_________联系起来。运动和力受力情况二、两类基本问题
(1)已知物体的受力情况,由_____________求出物体
的加速度,再通过___________确定物体的运动情况。
(2)已知物体的运动情况,根据___________求出物体
的加速度,再根据_____________确定物体所受的力。牛顿第二定律运动学规律运动学公式牛顿第二定律【思考辨析】
(1)物体的加速度方向就是其运动方向。 ( )
(2)同一个物体,其所受合外力越大,加速度越
大。( )
(3)同一个物体,其所受合外力越大,运动越
快。 ( )(4)对于任何运动物体,它在任何一段时间内的平均速度都等于该段时间初、末速度的平均值。( )
(5)物体运动状态的变化情况是由它的受力决定
的。 ( )提示:(1)×。物体的速度方向就是其运动方向,加速度的方向不一定与运动方向相同。
(2)√。由牛顿第二定律知,质量相同的物体,它的加速度大小与其合外力大小成正比。
(3)×。物体的运动快慢由其速度大小决定,与物体的合力大小无关。(4)×。“一段时间内的平均速度等于该段时间初、末速度的平均值”的结论只适用于匀变速直线运动,对一般的变速运动不适用。
(5)√。力是产生加速度的原因,物体的运动状态的变化情况是由它的受力情况决定的。一 从受力确定运动情况
考查角度1 由受力情况定性分析运动情况
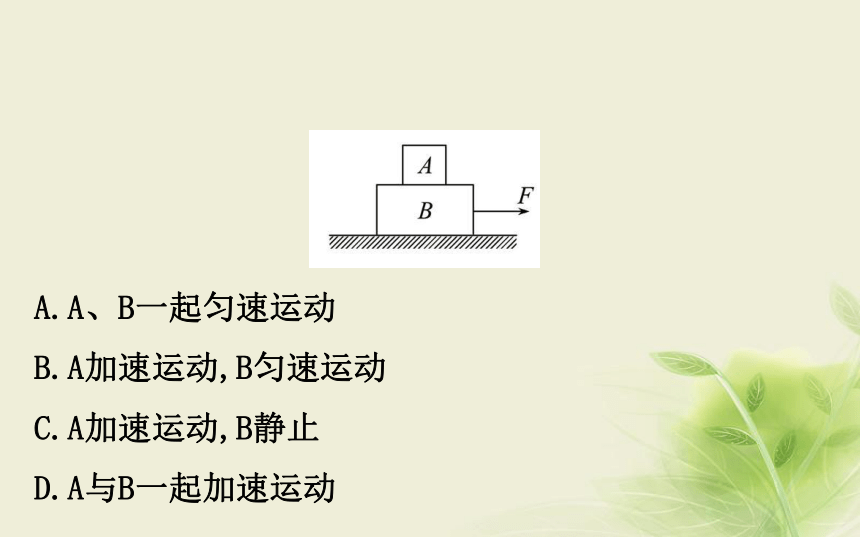
【典例1】(多选)在水平地面上,A、B两物体叠放如图所示,在水平力F的作用下一起匀速运动,若将水平力F作用在A上,两物体可能发生的情况是 ( )
导学号28974111A.A、B一起匀速运动
B.A加速运动,B匀速运动
C.A加速运动,B静止
D.A与B一起加速运动【正确解答】选A、C。若A、B间的最大静摩擦力大于F,则A、B仍一起做匀速直线运动,A正确;若A、B间的最大静摩擦力小于F,则A在拉力F的作用下做匀加速直线运动,而B受到A的滑动摩擦力小于B与地面间的滑动摩擦力(由题意可知此力大小与F相等),物块B保持静止,选项C正确。考查角度2 由受力情况定量计算运动情况
【典例2】如图所示,在海滨游乐场里有一种滑沙运动。某人坐在滑板上从斜坡的高处A点由静止开始滑下,滑到斜坡底端B点后,沿水平的滑道再滑行一段距离到C点停下来。若人和滑板的总质量m=60.0 kg,滑板与斜坡滑道和水平滑道间的动摩擦因数均为μ=0.5,斜坡的倾角θ=37°(sin 37°=0.6,cos 37°=0.8),斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10 m/s2。求: 导学号28974112
(1)人从斜坡上滑下的加速度为多大?
(2)若由于场地的限制,水平滑道BC的最大长度L=
20.0 m,则斜坡上A、B两点间的距离应不超过多少?【解题探究】
(1)人和滑板经历了怎样的运动过程?
提示:从A到B人和滑板做匀加速直线运动,从B到C人和滑板做匀减速直线运动。(2)人和滑板组成的系统在不同阶段分别受到哪些力的作用?
提示:分别分析人和滑板组成的系统在斜面上和平面上运动时的受力情况。【正确解答】(1)人和滑板在斜坡上的受力如图所示,建立直角坐标系。设人和滑板在斜坡上滑下的加速度为a1,由牛顿第二定律得mgsin θ-Ff=ma1,
FN-mgcos θ=0,
其中Ff=μFN,
联立解得人和滑板滑下的加速度为
a1=g(sin θ-μcos θ)=2.0 m/s2。(2)人和滑板在水平滑道上受力如图所示。由牛顿第二定律得
FN′-mg=0,Ff′=ma2,
其中Ff′=μFN′,联立解得人和滑板在水平滑道上运动的加速度大小为a2=μg=0.5×10 m/s2=5.0 m/s2,
设人从斜坡上滑下的最大距离为LAB,由匀变速直线运动公式得
=2a1LAB,0- =-2a2L
联立解得LAB=50.0 m。
答案:(1)2.0 m/s2 (2)50.0 m【核心归纳】
1.问题界定:已知物体受力情况确定运动情况,指的是在受力情况已知的条件下,判断出物体的运动状态或求出物体的速度和位移。2.解题思路:3.解题步骤:
(1)确定研究对象,对研究对象进行受力分析,并画出物体的受力分析图。
(2)根据力的合成或力的正交分解,求出物体所受的合外力或Fx、Fy。(3)根据牛顿第二定律求出物体运动的加速度。
(4)结合物体运动的初始条件,选择运动学公式,求解其他待求的运动学物理量。【易错提醒】
(1)合力方向与加速度的方向一定相同,所以我们可以根据加速度的方向确定合力方向,或根据合力方向确定加速度的方向。
(2)合力方向与速度方向无必然联系,加速度方向与速度方向也无必然联系。【过关训练】
1.(多选)如图所示,表示某小球所受的合力与时间关系,各段的合力大小相同,作用时间相同,设小球从静止开始运动,由此可以判定 ( )
A.小球向前运动,再返回停止
B.小球向前运动,再返回不会停止
C.小球始终向前运动
D.小球在4秒末速度为0【解析】选C、D。由图象可知,物体在奇数秒内,合力恒定不变,从静止开始做匀加速直线运动。偶数秒内力反向,由于惯性,物体仍沿原方向做匀减速直线运动,偶数秒末速度为零,周而复始,做单向直线运动。C、D正确。2.质量为4 kg的物体放在与水平面成30°角、足够长
的粗糙斜面底端,物体与斜面间的动摩擦因数μ= ,
作用在物体上的外力与斜面平行,随时间变化的图象如
图所示,外力作用在物体上的时间共8 s,根据所给条件
(sin 30°= ,cos 30°= ,g取10 m/s2)求:(1)物体所受的摩擦阻力为多大?
(2)物体在0~4 s内的加速度为多少?运动的位移为多少?
(3)物体从运动到停止走过的总位移为多少?【解析】(1)如图,对物体进行受力分析可得:G1=mgsin 30°=20 N,
FN=G2=mgcos 30°=20 N,
Ff=μFN= ×20 N=20 N。(2)由牛顿第二定律可得,0~4 s内物体的加速度:
a= =5 m/s2,
4 s时的速度:v1=at=20 m/s,
0~4 s内位移:x1= at2=40 m。(3)4~6 s内拉力为0,物体匀减速运动,加速度:
a′= m/s2=-10 m/s2,
物体运动2 s速度恰好减为0,通过的位移:
x2= ×2 m=20 m,
6~10 s和0~4 s运动相同,x3=x1=40 m,10~12 s和4~6 s运动相同,x4=x2=20 m,
由于G1=Ff,故12 s后物体将静止在斜面上;
物体运动的总位移:x=x1+x2+x3+x4=120 m。
答案:(1)20 N (2)5 m/s2 40 m (3)120 m【补偿训练】
1.(多选)(2016·全国卷Ⅱ改编)两实心小球甲和乙由
同一种材料制成,甲球质量大于乙球质量。两球在空
气中由静止下落,假设它们运动时受到的阻力与球的
半径成正比,与球的速率无关。若它们下落相同的距
离,则 ( )A.甲球用的时间比乙球长
B.甲球末速度的大小大于乙球末速度的大小
C.甲球加速度的大小小于乙球加速度的大小
D.甲球受到的阻力大于乙球受到的阻力【解析】选B、D。设小球的密度为ρ,其质量m=
设阻力与球的半径的比值为k,根据牛顿第二定律得:
a= ,由m甲>m乙,ρ甲=ρ乙,
可得r甲>r乙,所以a甲>a乙,选项C错误;由于两球由静止
下落,两小球下落相同的距离,则由x= at2,t2= ,
t甲A.物块可能匀速下滑
B.物块仍以加速度a匀加速下滑
C.物块将以大于a的加速度匀加速下滑
D.物块将以小于a的加速度匀加速下滑【解析】选C。根据物块的运动情况可知,加恒力F前、后,物块的受力情况分别如图甲、乙所示:则由牛顿第二定律得:
mgsinθ-μmgcosθ=ma,
(F+mg)sinθ-μ(F+mg)cosθ=ma′,两式相除得:
>1,所以a′>a,故只有C正确。3.如图所示,一个质量为4 kg的物体以v0=12 m/s的初速度沿着水平地面向左运动,物体与水平面间的动摩擦因数为0.2,物体始终受到一个水平向右、大小为12 N的恒力F作用(g取10 m/s2)。求:(1)开始时物体的加速度大小和方向。
(2)5 s末物体受到地面的摩擦力大小和方向。
(3)5 s末物体的速度。【解析】(1)物体受到向右的滑动摩擦力,
Ff=μFN=μmg=8 N。
根据牛顿第二定律得:F+Ff=ma
即a= =5 m/s2,方向水平向右。(2)物体减速到0所需的时间t= s=2.4 s
由于F>Ff,故物体速度减为零以后改为向右匀加速运动。2.4 s后摩擦力大小仍为8 N,方向水平向左。(3)2.4 s后物体的加速度:
a′= =1 m/s2,方向水平向右。
则5 s末的速度:
v=a′t′=1×(5-2.4)m/s=2.6 m/s,
方向水平向右。答案:(1)5 m/s2 方向水平向右
(2)8 N 方向水平向左
(3)2.6 m/s,方向水平向右二 从运动情况确定受力
【典例】如图所示的机车,质量为100 t,设它从停车场出发经225 m后速度达到54 km/h,此时,司机关闭发动机,让机车进站。机车又行驶了125 m才停在站上,设机车所受的阻力保持不变,关闭发动机前机车所受的牵引力不变,求机车关闭发动机前所受的牵引力。 导学号28974113【解题探究】
(1)关闭发动机前,机车的受力情况、运动情况如何?
提示:关闭发动机前,机车在水平方向受牵引力、阻力,做匀加速直线运动。
(2)关闭发动机后,机车的受力情况、运动情况如何?
提示:关闭发动机后,机车在水平方向受阻力,做匀减速直线运动。【正确解答】设机车在加速阶段的加速度为a1,减速阶段的加速度为a2
则:v2=2a1x1,
v2=2a2x2,
解得:a1=0.5 m/s2,a2=0.9 m/s2,由牛顿第二定律得
F-Ff=ma1,
Ff=ma2,
解得:F=1.4×105N。
答案:1.4×105N【核心归纳】
1.问题界定:已知物体运动情况确定受力情况,指的是在运动情况(如物体的运动性质、速度、加速度或位移)已知的条件下,要求得出物体所受的力。2.解题思路:3.解题步骤:
(1)确定研究对象,对研究对象进行受力分析和运动过程分析,并画出受力图和运动草图。
(2)选择合适的运动学公式,求出物体的加速度。
(3)根据牛顿第二定律列方程,求物体所受的合外力。
(4)根据力的合成与分解的方法,由合力求出所需的力。【易错提醒】
(1)分析、计算加速度和合力时,不仅要关注它们的大小,同时要确定它们的方向。
(2)已知合力求分力时,若所求分力与合力在一条直线上,可将矢量运算转化为算术运算;如果所求分力与合力不在一条直线上,需作出力的合成图,根据几何知识求解。【过关训练】
1.如图甲所示,一质量为M的木板静止在光滑水平地面上,现有一质量为m的小滑块以一定的初速度v0从木板的左端开始向木板的右端滑行,滑块和木板的水平速度大小随时间变化的情况如图乙所示,根据图象作出如下判断,不正确的是 ( )A.滑块始终与木板存在相对运动
B.滑块未能滑出木板
C.滑块的质量m大于木板的质量M
D.在t1时刻滑块从木板上滑出【解析】选B。由图象可知,在运动的过程中,滑块与木板的速度不同,始终与木板存在相对运动,A正确。滑块先做匀减速直线运动,木板先做匀加速直线运动,最终都做匀速直线运动,因为匀速直线运动的速度不同,则知滑块在t1时刻从木板上滑出,B错误,D正确;从图象的斜率可知,滑块的加速度大小小于木板加速度的大小,
根据牛顿第二定律知,a= ,两个物体所受的摩擦力大
小相等,可知滑块的质量m大于木板的质量M,C正确。
故选B。2.民用航空客机的机舱除通常的舱门外还设有紧急出
口,发生意外情况的飞机着陆后,打开紧急出口的舱门,
会自动生成一个由气囊组成的斜面,机舱中的乘客就
可以沿斜面迅速滑行到地面上来。若某型号的客机紧
急出口离地面高度为4.0 m,构成斜面的气囊长度为
5.0 m。要求紧急疏散时,乘客从气囊上由静止下滑到
达地面的时间不超过2.0 s(g取10 m/s2),则:(1)乘客在气囊上下滑的加速度至少为多大?
(2)气囊和下滑乘客间的动摩擦因数不得超过多少?【解析】(1)由题意可知,h=4.0 m,
L=5.0 m,t=2.0 s。
设斜面倾角为θ,则sin θ= 。
乘客沿气囊下滑过程中,
由L= at2得a=
代入数据得a=2.5 m/s2。(2)在乘客下滑过程中,对乘客受力分析如图所示,
沿x轴方向有
mgsin θ-Ff=ma,
沿y轴方向有FN-mgcos θ=0,
又Ff=μFN,联立方程解得
μ= ≈0.92。
答案:(1)2.5 m/s2 (2)0.92【补偿训练】
1.质量为1 kg的质点,受水平恒力作用,由静止开始做匀加速直线运动,它在t秒内的位移为x m,则合力F的大小为 ( )【解析】选A。由运动情况可求得质点的加速度
a= m/s2,则合力F=ma= N,A正确。2.一质量m=0.2 kg的小球从距水平地面H=10 m的高度无初速度释放,经t=2 s的时间到达地面,后经地面作用竖直反弹。每次与地面碰撞时间忽略不计。碰撞后速度大小不变;小球在空中所受的空气阻力大小Ff恒定。g取10 m/s2。求:
(1)在空中所受的空气阻力大小Ff。
(2)第一次碰撞后上升的最大高度。【解析】(1)小球下落时做匀加速直线运动,
由H= a1t2得
下落的加速度:a1= =5 m/s2,对小球,由牛顿第二定律得:mg-Ff=ma1,解得:Ff=1 N。(2)小球落地时的速度:v=a1t=10 m/s,由题意可知,
小球反弹后向上运动的初速度为10 m/s,小球向上
运动过程,加速度:a2= =15 m/s2,
小球向上做匀减速直线运动,由-v2=-2a2H′
得上升的最大高度:H′= m。
答案:(1)1 N (2) m【拓展例题】考查内容:牛顿第二定律与运动
图象综合问题
【典例】如图甲,一物体以一定的初速度从斜面底端沿斜面向上运动,上升到最高点后又沿斜面滑下,某段时间的速度-时间图象如图乙所示,g取10 m/s2,由此可知斜面倾角为 ( )A.30° B.37° C.53° D.60°【正确解答】选B。速度时间图象的斜率表示加速度,则由图可知,沿斜面上升时的加速度大小为
a1= m/s2=8 m/s2 ①
沿斜面下滑时的加速度大小为
a2= m/s2=4 m/s2 ②根据牛顿第二定律得:
上升时,有:a1= ③
下滑时,有:a2= ④
由①②③④解得:θ=37°
B正确。
用牛顿运动定律解决问题(一)一、牛顿第二定律的作用
确定了_________的关系,把物体的运动情况与
_________联系起来。运动和力受力情况二、两类基本问题
(1)已知物体的受力情况,由_____________求出物体
的加速度,再通过___________确定物体的运动情况。
(2)已知物体的运动情况,根据___________求出物体
的加速度,再根据_____________确定物体所受的力。牛顿第二定律运动学规律运动学公式牛顿第二定律【思考辨析】
(1)物体的加速度方向就是其运动方向。 ( )
(2)同一个物体,其所受合外力越大,加速度越
大。( )
(3)同一个物体,其所受合外力越大,运动越
快。 ( )(4)对于任何运动物体,它在任何一段时间内的平均速度都等于该段时间初、末速度的平均值。( )
(5)物体运动状态的变化情况是由它的受力决定
的。 ( )提示:(1)×。物体的速度方向就是其运动方向,加速度的方向不一定与运动方向相同。
(2)√。由牛顿第二定律知,质量相同的物体,它的加速度大小与其合外力大小成正比。
(3)×。物体的运动快慢由其速度大小决定,与物体的合力大小无关。(4)×。“一段时间内的平均速度等于该段时间初、末速度的平均值”的结论只适用于匀变速直线运动,对一般的变速运动不适用。
(5)√。力是产生加速度的原因,物体的运动状态的变化情况是由它的受力情况决定的。一 从受力确定运动情况
考查角度1 由受力情况定性分析运动情况
【典例1】(多选)在水平地面上,A、B两物体叠放如图所示,在水平力F的作用下一起匀速运动,若将水平力F作用在A上,两物体可能发生的情况是 ( )
导学号28974111A.A、B一起匀速运动
B.A加速运动,B匀速运动
C.A加速运动,B静止
D.A与B一起加速运动【正确解答】选A、C。若A、B间的最大静摩擦力大于F,则A、B仍一起做匀速直线运动,A正确;若A、B间的最大静摩擦力小于F,则A在拉力F的作用下做匀加速直线运动,而B受到A的滑动摩擦力小于B与地面间的滑动摩擦力(由题意可知此力大小与F相等),物块B保持静止,选项C正确。考查角度2 由受力情况定量计算运动情况
【典例2】如图所示,在海滨游乐场里有一种滑沙运动。某人坐在滑板上从斜坡的高处A点由静止开始滑下,滑到斜坡底端B点后,沿水平的滑道再滑行一段距离到C点停下来。若人和滑板的总质量m=60.0 kg,滑板与斜坡滑道和水平滑道间的动摩擦因数均为μ=0.5,斜坡的倾角θ=37°(sin 37°=0.6,cos 37°=0.8),斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10 m/s2。求: 导学号28974112
(1)人从斜坡上滑下的加速度为多大?
(2)若由于场地的限制,水平滑道BC的最大长度L=
20.0 m,则斜坡上A、B两点间的距离应不超过多少?【解题探究】
(1)人和滑板经历了怎样的运动过程?
提示:从A到B人和滑板做匀加速直线运动,从B到C人和滑板做匀减速直线运动。(2)人和滑板组成的系统在不同阶段分别受到哪些力的作用?
提示:分别分析人和滑板组成的系统在斜面上和平面上运动时的受力情况。【正确解答】(1)人和滑板在斜坡上的受力如图所示,建立直角坐标系。设人和滑板在斜坡上滑下的加速度为a1,由牛顿第二定律得mgsin θ-Ff=ma1,
FN-mgcos θ=0,
其中Ff=μFN,
联立解得人和滑板滑下的加速度为
a1=g(sin θ-μcos θ)=2.0 m/s2。(2)人和滑板在水平滑道上受力如图所示。由牛顿第二定律得
FN′-mg=0,Ff′=ma2,
其中Ff′=μFN′,联立解得人和滑板在水平滑道上运动的加速度大小为a2=μg=0.5×10 m/s2=5.0 m/s2,
设人从斜坡上滑下的最大距离为LAB,由匀变速直线运动公式得
=2a1LAB,0- =-2a2L
联立解得LAB=50.0 m。
答案:(1)2.0 m/s2 (2)50.0 m【核心归纳】
1.问题界定:已知物体受力情况确定运动情况,指的是在受力情况已知的条件下,判断出物体的运动状态或求出物体的速度和位移。2.解题思路:3.解题步骤:
(1)确定研究对象,对研究对象进行受力分析,并画出物体的受力分析图。
(2)根据力的合成或力的正交分解,求出物体所受的合外力或Fx、Fy。(3)根据牛顿第二定律求出物体运动的加速度。
(4)结合物体运动的初始条件,选择运动学公式,求解其他待求的运动学物理量。【易错提醒】
(1)合力方向与加速度的方向一定相同,所以我们可以根据加速度的方向确定合力方向,或根据合力方向确定加速度的方向。
(2)合力方向与速度方向无必然联系,加速度方向与速度方向也无必然联系。【过关训练】
1.(多选)如图所示,表示某小球所受的合力与时间关系,各段的合力大小相同,作用时间相同,设小球从静止开始运动,由此可以判定 ( )
A.小球向前运动,再返回停止
B.小球向前运动,再返回不会停止
C.小球始终向前运动
D.小球在4秒末速度为0【解析】选C、D。由图象可知,物体在奇数秒内,合力恒定不变,从静止开始做匀加速直线运动。偶数秒内力反向,由于惯性,物体仍沿原方向做匀减速直线运动,偶数秒末速度为零,周而复始,做单向直线运动。C、D正确。2.质量为4 kg的物体放在与水平面成30°角、足够长
的粗糙斜面底端,物体与斜面间的动摩擦因数μ= ,
作用在物体上的外力与斜面平行,随时间变化的图象如
图所示,外力作用在物体上的时间共8 s,根据所给条件
(sin 30°= ,cos 30°= ,g取10 m/s2)求:(1)物体所受的摩擦阻力为多大?
(2)物体在0~4 s内的加速度为多少?运动的位移为多少?
(3)物体从运动到停止走过的总位移为多少?【解析】(1)如图,对物体进行受力分析可得:G1=mgsin 30°=20 N,
FN=G2=mgcos 30°=20 N,
Ff=μFN= ×20 N=20 N。(2)由牛顿第二定律可得,0~4 s内物体的加速度:
a= =5 m/s2,
4 s时的速度:v1=at=20 m/s,
0~4 s内位移:x1= at2=40 m。(3)4~6 s内拉力为0,物体匀减速运动,加速度:
a′= m/s2=-10 m/s2,
物体运动2 s速度恰好减为0,通过的位移:
x2= ×2 m=20 m,
6~10 s和0~4 s运动相同,x3=x1=40 m,10~12 s和4~6 s运动相同,x4=x2=20 m,
由于G1=Ff,故12 s后物体将静止在斜面上;
物体运动的总位移:x=x1+x2+x3+x4=120 m。
答案:(1)20 N (2)5 m/s2 40 m (3)120 m【补偿训练】
1.(多选)(2016·全国卷Ⅱ改编)两实心小球甲和乙由
同一种材料制成,甲球质量大于乙球质量。两球在空
气中由静止下落,假设它们运动时受到的阻力与球的
半径成正比,与球的速率无关。若它们下落相同的距
离,则 ( )A.甲球用的时间比乙球长
B.甲球末速度的大小大于乙球末速度的大小
C.甲球加速度的大小小于乙球加速度的大小
D.甲球受到的阻力大于乙球受到的阻力【解析】选B、D。设小球的密度为ρ,其质量m=
设阻力与球的半径的比值为k,根据牛顿第二定律得:
a= ,由m甲>m乙,ρ甲=ρ乙,
可得r甲>r乙,所以a甲>a乙,选项C错误;由于两球由静止
下落,两小球下落相同的距离,则由x= at2,t2= ,
t甲
B.物块仍以加速度a匀加速下滑
C.物块将以大于a的加速度匀加速下滑
D.物块将以小于a的加速度匀加速下滑【解析】选C。根据物块的运动情况可知,加恒力F前、后,物块的受力情况分别如图甲、乙所示:则由牛顿第二定律得:
mgsinθ-μmgcosθ=ma,
(F+mg)sinθ-μ(F+mg)cosθ=ma′,两式相除得:
>1,所以a′>a,故只有C正确。3.如图所示,一个质量为4 kg的物体以v0=12 m/s的初速度沿着水平地面向左运动,物体与水平面间的动摩擦因数为0.2,物体始终受到一个水平向右、大小为12 N的恒力F作用(g取10 m/s2)。求:(1)开始时物体的加速度大小和方向。
(2)5 s末物体受到地面的摩擦力大小和方向。
(3)5 s末物体的速度。【解析】(1)物体受到向右的滑动摩擦力,
Ff=μFN=μmg=8 N。
根据牛顿第二定律得:F+Ff=ma
即a= =5 m/s2,方向水平向右。(2)物体减速到0所需的时间t= s=2.4 s
由于F>Ff,故物体速度减为零以后改为向右匀加速运动。2.4 s后摩擦力大小仍为8 N,方向水平向左。(3)2.4 s后物体的加速度:
a′= =1 m/s2,方向水平向右。
则5 s末的速度:
v=a′t′=1×(5-2.4)m/s=2.6 m/s,
方向水平向右。答案:(1)5 m/s2 方向水平向右
(2)8 N 方向水平向左
(3)2.6 m/s,方向水平向右二 从运动情况确定受力
【典例】如图所示的机车,质量为100 t,设它从停车场出发经225 m后速度达到54 km/h,此时,司机关闭发动机,让机车进站。机车又行驶了125 m才停在站上,设机车所受的阻力保持不变,关闭发动机前机车所受的牵引力不变,求机车关闭发动机前所受的牵引力。 导学号28974113【解题探究】
(1)关闭发动机前,机车的受力情况、运动情况如何?
提示:关闭发动机前,机车在水平方向受牵引力、阻力,做匀加速直线运动。
(2)关闭发动机后,机车的受力情况、运动情况如何?
提示:关闭发动机后,机车在水平方向受阻力,做匀减速直线运动。【正确解答】设机车在加速阶段的加速度为a1,减速阶段的加速度为a2
则:v2=2a1x1,
v2=2a2x2,
解得:a1=0.5 m/s2,a2=0.9 m/s2,由牛顿第二定律得
F-Ff=ma1,
Ff=ma2,
解得:F=1.4×105N。
答案:1.4×105N【核心归纳】
1.问题界定:已知物体运动情况确定受力情况,指的是在运动情况(如物体的运动性质、速度、加速度或位移)已知的条件下,要求得出物体所受的力。2.解题思路:3.解题步骤:
(1)确定研究对象,对研究对象进行受力分析和运动过程分析,并画出受力图和运动草图。
(2)选择合适的运动学公式,求出物体的加速度。
(3)根据牛顿第二定律列方程,求物体所受的合外力。
(4)根据力的合成与分解的方法,由合力求出所需的力。【易错提醒】
(1)分析、计算加速度和合力时,不仅要关注它们的大小,同时要确定它们的方向。
(2)已知合力求分力时,若所求分力与合力在一条直线上,可将矢量运算转化为算术运算;如果所求分力与合力不在一条直线上,需作出力的合成图,根据几何知识求解。【过关训练】
1.如图甲所示,一质量为M的木板静止在光滑水平地面上,现有一质量为m的小滑块以一定的初速度v0从木板的左端开始向木板的右端滑行,滑块和木板的水平速度大小随时间变化的情况如图乙所示,根据图象作出如下判断,不正确的是 ( )A.滑块始终与木板存在相对运动
B.滑块未能滑出木板
C.滑块的质量m大于木板的质量M
D.在t1时刻滑块从木板上滑出【解析】选B。由图象可知,在运动的过程中,滑块与木板的速度不同,始终与木板存在相对运动,A正确。滑块先做匀减速直线运动,木板先做匀加速直线运动,最终都做匀速直线运动,因为匀速直线运动的速度不同,则知滑块在t1时刻从木板上滑出,B错误,D正确;从图象的斜率可知,滑块的加速度大小小于木板加速度的大小,
根据牛顿第二定律知,a= ,两个物体所受的摩擦力大
小相等,可知滑块的质量m大于木板的质量M,C正确。
故选B。2.民用航空客机的机舱除通常的舱门外还设有紧急出
口,发生意外情况的飞机着陆后,打开紧急出口的舱门,
会自动生成一个由气囊组成的斜面,机舱中的乘客就
可以沿斜面迅速滑行到地面上来。若某型号的客机紧
急出口离地面高度为4.0 m,构成斜面的气囊长度为
5.0 m。要求紧急疏散时,乘客从气囊上由静止下滑到
达地面的时间不超过2.0 s(g取10 m/s2),则:(1)乘客在气囊上下滑的加速度至少为多大?
(2)气囊和下滑乘客间的动摩擦因数不得超过多少?【解析】(1)由题意可知,h=4.0 m,
L=5.0 m,t=2.0 s。
设斜面倾角为θ,则sin θ= 。
乘客沿气囊下滑过程中,
由L= at2得a=
代入数据得a=2.5 m/s2。(2)在乘客下滑过程中,对乘客受力分析如图所示,
沿x轴方向有
mgsin θ-Ff=ma,
沿y轴方向有FN-mgcos θ=0,
又Ff=μFN,联立方程解得
μ= ≈0.92。
答案:(1)2.5 m/s2 (2)0.92【补偿训练】
1.质量为1 kg的质点,受水平恒力作用,由静止开始做匀加速直线运动,它在t秒内的位移为x m,则合力F的大小为 ( )【解析】选A。由运动情况可求得质点的加速度
a= m/s2,则合力F=ma= N,A正确。2.一质量m=0.2 kg的小球从距水平地面H=10 m的高度无初速度释放,经t=2 s的时间到达地面,后经地面作用竖直反弹。每次与地面碰撞时间忽略不计。碰撞后速度大小不变;小球在空中所受的空气阻力大小Ff恒定。g取10 m/s2。求:
(1)在空中所受的空气阻力大小Ff。
(2)第一次碰撞后上升的最大高度。【解析】(1)小球下落时做匀加速直线运动,
由H= a1t2得
下落的加速度:a1= =5 m/s2,对小球,由牛顿第二定律得:mg-Ff=ma1,解得:Ff=1 N。(2)小球落地时的速度:v=a1t=10 m/s,由题意可知,
小球反弹后向上运动的初速度为10 m/s,小球向上
运动过程,加速度:a2= =15 m/s2,
小球向上做匀减速直线运动,由-v2=-2a2H′
得上升的最大高度:H′= m。
答案:(1)1 N (2) m【拓展例题】考查内容:牛顿第二定律与运动
图象综合问题
【典例】如图甲,一物体以一定的初速度从斜面底端沿斜面向上运动,上升到最高点后又沿斜面滑下,某段时间的速度-时间图象如图乙所示,g取10 m/s2,由此可知斜面倾角为 ( )A.30° B.37° C.53° D.60°【正确解答】选B。速度时间图象的斜率表示加速度,则由图可知,沿斜面上升时的加速度大小为
a1= m/s2=8 m/s2 ①
沿斜面下滑时的加速度大小为
a2= m/s2=4 m/s2 ②根据牛顿第二定律得:
上升时,有:a1= ③
下滑时,有:a2= ④
由①②③④解得:θ=37°
B正确。
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
