3.2弹力 课后提升训练
文档属性
| 名称 | 3.2弹力 课后提升训练 | 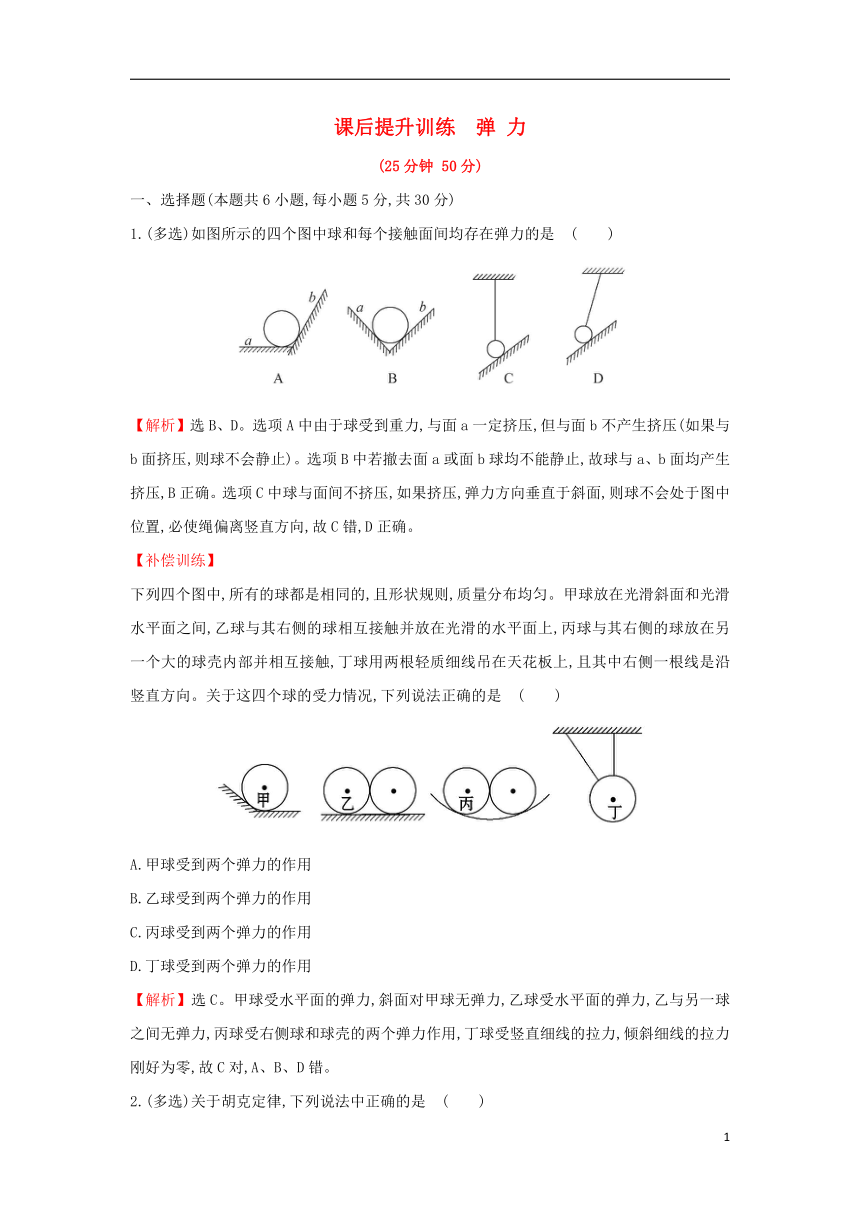 | |
| 格式 | zip | ||
| 文件大小 | 158.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-10-03 22:25:29 | ||
图片预览



文档简介
课后提升训练 弹 力
(25分钟 50分)
一、选择题(本题共6小题,每小题5分,共30分)
1.(多选)如图所示的四个图中球和每个接触面间均存在弹力的是 ( )
【解析】选B、D。选项A中由于球受到重力,与面a一定挤压,但与面b不产生挤压(如果与b面挤压,则球不会静止)。选项B中若撤去面a或面b球均不能静止,故球与a、b面均产生挤压,B正确。选项C中球与面间不挤压,如果挤压,弹力方向垂直于斜面,则球不会处于图中位置,必使绳偏离竖直方向,故C错,D正确。
【补偿训练】
下列四个图中,所有的球都是相同的,且形状规则,质量分布均匀。甲球放在光滑斜面和光滑水平面之间,乙球与其右侧的球相互接触并放在光滑的水平面上,丙球与其右侧的球放在另一个大的球壳内部并相互接触,丁球用两根轻质细线吊在天花板上,且其中右侧一根线是沿竖直方向。关于这四个球的受力情况,下列说法正确的是 ( )
A.甲球受到两个弹力的作用
B.乙球受到两个弹力的作用
C.丙球受到两个弹力的作用
D.丁球受到两个弹力的作用
【解析】选C。甲球受水平面的弹力,斜面对甲球无弹力,乙球受水平面的弹力,乙与另一球之间无弹力,丙球受右侧球和球壳的两个弹力作用,丁球受竖直细线的拉力,倾斜细线的拉力刚好为零,故C对,A、B、D错。
2.(多选)关于胡克定律,下列说法中正确的是 ( )
A.由F=kx可知,弹力F的大小与弹簧的长度x成正比
B.由k=可知,劲度系数k与弹力F成正比,与弹簧长度的改变量x成反比
C.弹簧的劲度系数k是由弹簧本身的性质决定的,与弹力F的大小和弹簧形变量x的大小无关
D.弹簧的劲度系数在数值上等于弹簧伸长(或缩短)单位长度时弹力的大小
【解析】选C、D。胡克定律F=kx中,x是弹簧伸长或缩短的长度;k是劲度系数,与弹簧本身的性质有关,与F、x均无关,故A、B错误,C、D正确。
3.(多选)如图所示,小球A的重力G=20N,上端通过竖直悬线挂于O点,下端与水平桌面相接触,悬线对球A、水平桌面对球A的弹力大小可能为 ( )
A.0,G B.G,0
C., D.G,G
【解析】选A、B、C。球A处于静止状态,球A所受的力为平衡力,即线对球的拉力FT及桌面对球的弹力FN共同作用与重力G平衡,即FT+FN=G,若线恰好伸直,则FT=0,FN=G,A正确。若球刚好离开桌面,则FN=0,FT=G,B正确。也可能FN=FT=,C正确。
4.(2017·大庆高一检测)如图所示,一劲度系数为k的弹簧,下端悬挂一重物,重物质量为m,平衡时物体在a位置,现用力将物体向下拉长x至b位置,则此时弹簧的弹力为 ( )
A.kx B.mg+kx
C.mg-kx D.以上说法都不正确
【解析】选B。题中给出的x并非在原长基础上的形变量,因此弹力F≠kx,故选项A错误;开始时,物体在位置a静止,此时弹力与重力平衡,即F1=mg,由F1=kx知,弹簧伸长量x1=,又因为拉力使弹簧又伸长了x,则弹簧总的形变量为x1+x=+x,故弹簧弹力为F2=k(+x)=mg+kx,故选项B正确。
5.两个劲度系数分别为k1和k2的轻质弹簧a、b串接在一起,a弹簧的一端固定在墙上,如图所示。开始时弹簧均处于原长状态,现用水平力作用在b弹簧的p端向右拉动弹簧,已知a弹簧的伸长量为L,则 ( )
A.b弹簧的伸长量也为L
B.b弹簧的伸长量为
C.p端向右移动的距离为2L
D.p端向右移动的距离为(1+)L
【解析】选B。两弹簧的弹力相等,由F=kx,得b弹簧的伸长量为,p端向右移动的距离为L+=(1+)L,B正确。
【补偿训练】
如图所示,两个重物P、Q与两根弹簧连接。设两弹簧共伸长L,现用手向上托重物Q,缓慢上移L后停止,下列结论正确的是 ( )
A.两弹簧均变为自由长
B.Ⅰ弹簧比自由长短,Ⅱ弹簧比自由长长
C.Ⅰ弹簧比自由长长,Ⅱ弹簧比自由长短
D.Ⅰ弹簧比自由长长,Ⅱ弹簧恰为自由长
【解析】选C。假设两弹簧均变为原长,则重物P只受重力,不能平衡,故重物P一定会向下运动导致Ⅰ弹簧比自由长长,Ⅱ弹簧比自由长短。
6.一个实验小组在“探究弹力和弹簧伸长量的关系”的实验中,使用两条不同的轻质弹簧a和b,得到弹力与弹簧长度的图象如图所示。下列表述正确的
是 ( )
A.a的原长比b的长
B.a的劲度系数比b的大
C.a的劲度系数比b的小
D.测得的弹力与弹簧的长度成正比
【解题指南】解答本题应把握以下两点:
(1)F-l图象中直线的斜率表示弹簧的劲度系数。
(2)F-l图象中横轴上的截距表示弹簧的原长。
【解析】选B。在图象中横截距表示弹簧的原长,故a的原长比b的短,故A错误;在图象中斜率表示弹簧的劲度系数k,故a的劲度系数比b的大,故B正确、C错误;弹簧的弹力满足胡克定律,弹力与弹簧的形变量成正比,故D错误。
二、非选择题(本题共2小题,共20分)
7.(10分)(2017·淮北高一检测)探究弹力和弹簧伸长的关系时,在弹性限度内,悬挂15N重物时,弹簧长度为0.16 m,悬挂20 N重物时,弹簧长度为0.18 m,求弹簧的原长L0和劲度系数k。
【解析】由胡克定律可得:
F1=k(L1-L0) ①
F2=k(L2-L0) ②
由①②代入数据解得:
L0=0.10m
k=250N/m。
答案:0.10m 250 N/m
8.(10分)一根弹簧的伸长(ΔL)和所受的外力(F)之间的关系如图所示,弹簧原长L0为50cm,试根据图象回答:
(1)若要使弹簧伸长到60cm,需要多大拉力?
(2)如果用900N的拉力(仍在弹性限度内),弹簧长度变为多少?
【解析】(1)由题图可得:弹簧伸长ΔL1=L1-L0=(60-50)cm=10 cm,需要拉力为F1=300N。
(2)当拉力为F2=900N时,弹簧伸长ΔL2=30cm,所以弹簧长度变为L2=L0+ΔL2=(50+30)cm=80 cm。
答案:(1)300N (2)80 cm
【延伸探究】将上题中的弹簧压缩到35cm,需要多大的力?
提示:F3=k(L0-L3) k=
解得:F3=450N
答案:450N
【补偿训练】在现代汽车技术中,一般轿车都设置有“汽车悬架”,麦弗逊式及烛式悬架都是将螺旋弹簧和减振器有机结合,对缓冲冲击和削减冲击产生的振动全面考虑,大大提高了乘坐者的舒适性。现在有一组合弹簧,一根大弹簧内套了一根小弹簧,大弹簧比小弹簧长0.2m。为了测量弹簧的劲度系数,把组合弹簧的一端平齐并竖直固定,另一端处于自由状态,如图甲所示。当压缩此组合弹簧时,测得力与压缩距离之间的关系图线如图乙所示,则大弹簧的劲度系数k1和小弹簧的劲度系数k2分别为多少?
【解析】从题图可知,压缩距离x在0~0.2m范围内,有F=k1x,此时只有大弹簧起作用,小弹簧并没有承受压力,所以大弹簧的劲度系数k1=10N/m;压缩距离x在0.2~0.3m范围内,两个弹簧都被压缩,都产生弹力,当大弹簧压缩了x时,小弹簧压缩了(x-0.2)m,所以F=k1x+k2(x-0.2),由图中数据可求得k2=20N/m。
答案:10N/m 20N/m
(25分钟 50分)
一、选择题(本题共6小题,每小题5分,共30分)
1.(多选)如图所示的四个图中球和每个接触面间均存在弹力的是 ( )
【解析】选B、D。选项A中由于球受到重力,与面a一定挤压,但与面b不产生挤压(如果与b面挤压,则球不会静止)。选项B中若撤去面a或面b球均不能静止,故球与a、b面均产生挤压,B正确。选项C中球与面间不挤压,如果挤压,弹力方向垂直于斜面,则球不会处于图中位置,必使绳偏离竖直方向,故C错,D正确。
【补偿训练】
下列四个图中,所有的球都是相同的,且形状规则,质量分布均匀。甲球放在光滑斜面和光滑水平面之间,乙球与其右侧的球相互接触并放在光滑的水平面上,丙球与其右侧的球放在另一个大的球壳内部并相互接触,丁球用两根轻质细线吊在天花板上,且其中右侧一根线是沿竖直方向。关于这四个球的受力情况,下列说法正确的是 ( )
A.甲球受到两个弹力的作用
B.乙球受到两个弹力的作用
C.丙球受到两个弹力的作用
D.丁球受到两个弹力的作用
【解析】选C。甲球受水平面的弹力,斜面对甲球无弹力,乙球受水平面的弹力,乙与另一球之间无弹力,丙球受右侧球和球壳的两个弹力作用,丁球受竖直细线的拉力,倾斜细线的拉力刚好为零,故C对,A、B、D错。
2.(多选)关于胡克定律,下列说法中正确的是 ( )
A.由F=kx可知,弹力F的大小与弹簧的长度x成正比
B.由k=可知,劲度系数k与弹力F成正比,与弹簧长度的改变量x成反比
C.弹簧的劲度系数k是由弹簧本身的性质决定的,与弹力F的大小和弹簧形变量x的大小无关
D.弹簧的劲度系数在数值上等于弹簧伸长(或缩短)单位长度时弹力的大小
【解析】选C、D。胡克定律F=kx中,x是弹簧伸长或缩短的长度;k是劲度系数,与弹簧本身的性质有关,与F、x均无关,故A、B错误,C、D正确。
3.(多选)如图所示,小球A的重力G=20N,上端通过竖直悬线挂于O点,下端与水平桌面相接触,悬线对球A、水平桌面对球A的弹力大小可能为 ( )
A.0,G B.G,0
C., D.G,G
【解析】选A、B、C。球A处于静止状态,球A所受的力为平衡力,即线对球的拉力FT及桌面对球的弹力FN共同作用与重力G平衡,即FT+FN=G,若线恰好伸直,则FT=0,FN=G,A正确。若球刚好离开桌面,则FN=0,FT=G,B正确。也可能FN=FT=,C正确。
4.(2017·大庆高一检测)如图所示,一劲度系数为k的弹簧,下端悬挂一重物,重物质量为m,平衡时物体在a位置,现用力将物体向下拉长x至b位置,则此时弹簧的弹力为 ( )
A.kx B.mg+kx
C.mg-kx D.以上说法都不正确
【解析】选B。题中给出的x并非在原长基础上的形变量,因此弹力F≠kx,故选项A错误;开始时,物体在位置a静止,此时弹力与重力平衡,即F1=mg,由F1=kx知,弹簧伸长量x1=,又因为拉力使弹簧又伸长了x,则弹簧总的形变量为x1+x=+x,故弹簧弹力为F2=k(+x)=mg+kx,故选项B正确。
5.两个劲度系数分别为k1和k2的轻质弹簧a、b串接在一起,a弹簧的一端固定在墙上,如图所示。开始时弹簧均处于原长状态,现用水平力作用在b弹簧的p端向右拉动弹簧,已知a弹簧的伸长量为L,则 ( )
A.b弹簧的伸长量也为L
B.b弹簧的伸长量为
C.p端向右移动的距离为2L
D.p端向右移动的距离为(1+)L
【解析】选B。两弹簧的弹力相等,由F=kx,得b弹簧的伸长量为,p端向右移动的距离为L+=(1+)L,B正确。
【补偿训练】
如图所示,两个重物P、Q与两根弹簧连接。设两弹簧共伸长L,现用手向上托重物Q,缓慢上移L后停止,下列结论正确的是 ( )
A.两弹簧均变为自由长
B.Ⅰ弹簧比自由长短,Ⅱ弹簧比自由长长
C.Ⅰ弹簧比自由长长,Ⅱ弹簧比自由长短
D.Ⅰ弹簧比自由长长,Ⅱ弹簧恰为自由长
【解析】选C。假设两弹簧均变为原长,则重物P只受重力,不能平衡,故重物P一定会向下运动导致Ⅰ弹簧比自由长长,Ⅱ弹簧比自由长短。
6.一个实验小组在“探究弹力和弹簧伸长量的关系”的实验中,使用两条不同的轻质弹簧a和b,得到弹力与弹簧长度的图象如图所示。下列表述正确的
是 ( )
A.a的原长比b的长
B.a的劲度系数比b的大
C.a的劲度系数比b的小
D.测得的弹力与弹簧的长度成正比
【解题指南】解答本题应把握以下两点:
(1)F-l图象中直线的斜率表示弹簧的劲度系数。
(2)F-l图象中横轴上的截距表示弹簧的原长。
【解析】选B。在图象中横截距表示弹簧的原长,故a的原长比b的短,故A错误;在图象中斜率表示弹簧的劲度系数k,故a的劲度系数比b的大,故B正确、C错误;弹簧的弹力满足胡克定律,弹力与弹簧的形变量成正比,故D错误。
二、非选择题(本题共2小题,共20分)
7.(10分)(2017·淮北高一检测)探究弹力和弹簧伸长的关系时,在弹性限度内,悬挂15N重物时,弹簧长度为0.16 m,悬挂20 N重物时,弹簧长度为0.18 m,求弹簧的原长L0和劲度系数k。
【解析】由胡克定律可得:
F1=k(L1-L0) ①
F2=k(L2-L0) ②
由①②代入数据解得:
L0=0.10m
k=250N/m。
答案:0.10m 250 N/m
8.(10分)一根弹簧的伸长(ΔL)和所受的外力(F)之间的关系如图所示,弹簧原长L0为50cm,试根据图象回答:
(1)若要使弹簧伸长到60cm,需要多大拉力?
(2)如果用900N的拉力(仍在弹性限度内),弹簧长度变为多少?
【解析】(1)由题图可得:弹簧伸长ΔL1=L1-L0=(60-50)cm=10 cm,需要拉力为F1=300N。
(2)当拉力为F2=900N时,弹簧伸长ΔL2=30cm,所以弹簧长度变为L2=L0+ΔL2=(50+30)cm=80 cm。
答案:(1)300N (2)80 cm
【延伸探究】将上题中的弹簧压缩到35cm,需要多大的力?
提示:F3=k(L0-L3) k=
解得:F3=450N
答案:450N
【补偿训练】在现代汽车技术中,一般轿车都设置有“汽车悬架”,麦弗逊式及烛式悬架都是将螺旋弹簧和减振器有机结合,对缓冲冲击和削减冲击产生的振动全面考虑,大大提高了乘坐者的舒适性。现在有一组合弹簧,一根大弹簧内套了一根小弹簧,大弹簧比小弹簧长0.2m。为了测量弹簧的劲度系数,把组合弹簧的一端平齐并竖直固定,另一端处于自由状态,如图甲所示。当压缩此组合弹簧时,测得力与压缩距离之间的关系图线如图乙所示,则大弹簧的劲度系数k1和小弹簧的劲度系数k2分别为多少?
【解析】从题图可知,压缩距离x在0~0.2m范围内,有F=k1x,此时只有大弹簧起作用,小弹簧并没有承受压力,所以大弹簧的劲度系数k1=10N/m;压缩距离x在0.2~0.3m范围内,两个弹簧都被压缩,都产生弹力,当大弹簧压缩了x时,小弹簧压缩了(x-0.2)m,所以F=k1x+k2(x-0.2),由图中数据可求得k2=20N/m。
答案:10N/m 20N/m
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
