人教版数学六上数与形课件(共37张)
图片预览




文档简介
课件37张PPT。第 1 课时 数与形8 数学广角—数与形RJ 六年级上册 (1)认识正方形数
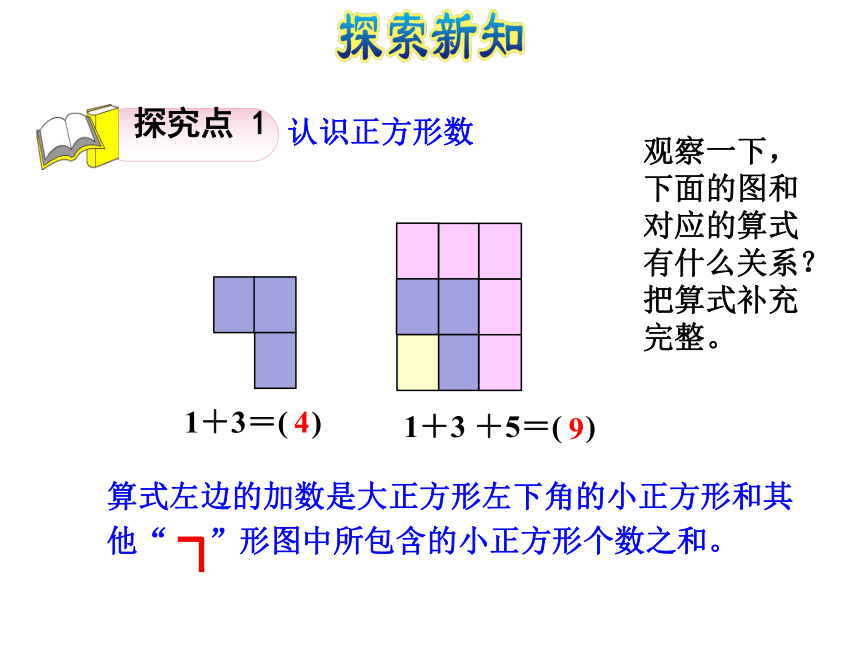
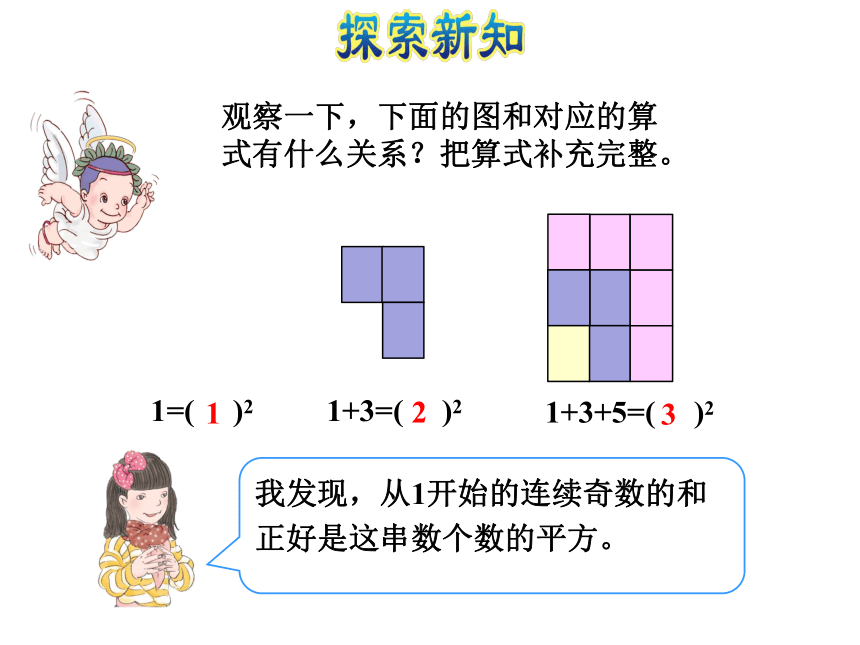
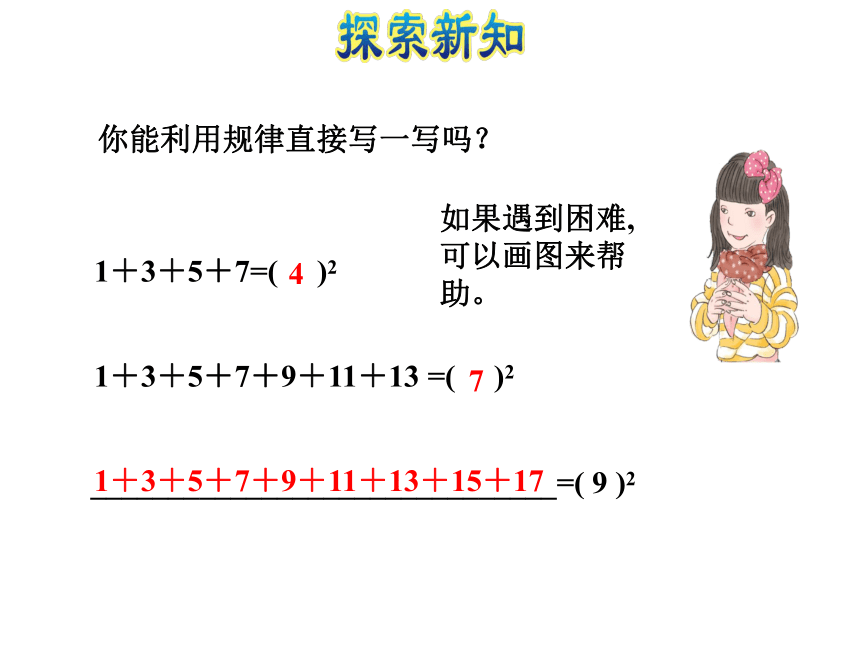
(2)初步感受极限思想课后作业探索新知课堂总结当堂检测新课导入计算出结果。1+3=( )41+3 +5=( ) 9 1+3+5+7=( )161+3+5+7+9+…+21=( )?认识正方形数观察一下,下面的图和对应的算式有什么关系?把算式补充完整。1+3=( )41+3 +5=( ) 9 1=( )21+3=( )21+3+5=( )2观察一下,下面的图和对应的算式有什么关系?把算式补充完整。123你能利用规律直接写一写吗?如果遇到困难,可以画图来帮助。1+3+5+7=( )21+3+5+7+9+11+13 =( )21+3+5+7+9+11+13+15+1747______________________________=( 9 )2归纳总结:解决这类问题可以通过数形结合的思想,通过构造与之相适应的图形,通过探究图形的规律率解决问题。1+3+5+7+5+3+1 =( ) 请根据例1的结论算一算。 (选题源于教材P108做一做第1题)可以看成两部分:1+3+5+7=42
5+3+1= 32 42+ 32 =25
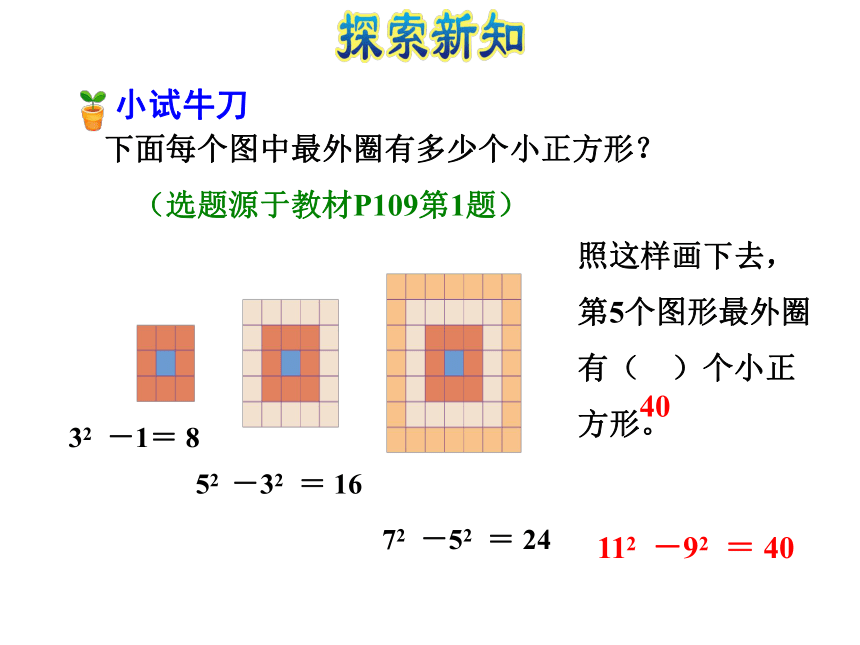
251+3+5+7+9+11+13+11+9+7+5+3+1=( )85下面每个图中最外圈有多少个小正方形?
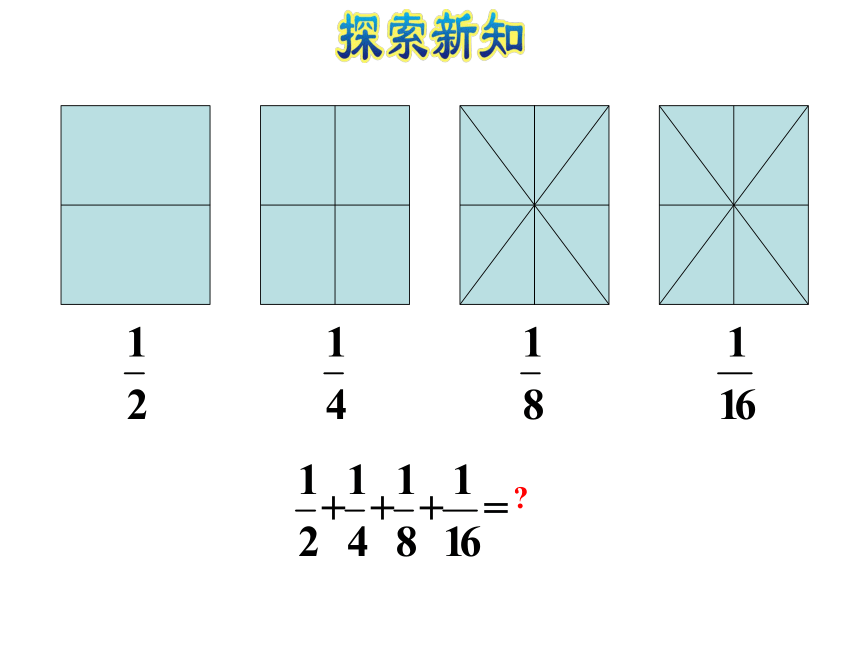
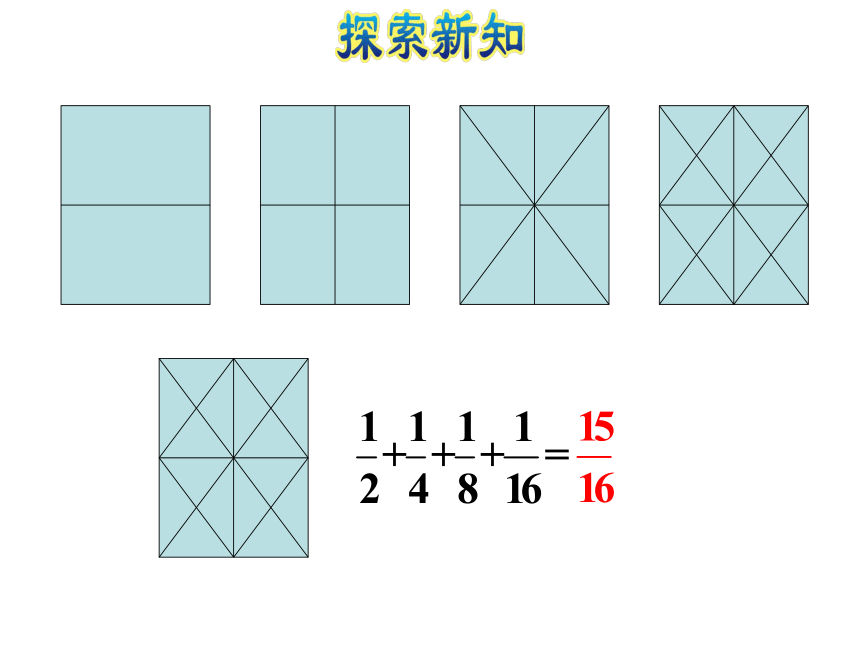
(选题源于教材P109第1题)照这样画下去,第5个图形最外圈有( )个小正方形。4032 -1= 852 -32 = 1672 -52 = 24112 -92 = 40?初步感受极限思想例2 在这列数中,你能发现什么规律? 从第二个数开始,每个数是前一个数的 。 计算 算一算、猜一猜,结果可能是多少?然后借助线段图或圆形图来帮助思考,验证你的猜测是否正确? ……加下去,等号右边的分数越来越接近于1。计算。线段图理解 有些问题通过画图,解决起来更直观、容易。 计算 1计算。圆形图理解 …… 先在图形上表示出 ,再表示出 , , 等,并不断地累加下去,其结果越来越接近1。当这个过程无止境地持续下去时,相加之和为1,这种数学思考方式体现了极限思想。 极限思想如上图所示: 的和等于单位“1”减去最后一个小正方形的面积,即 。除了借助线段图和圆形图进行理解,我们还可以用什么图形表示单位“1”呢?想一想:用一个正方形表示单位“1”:归纳总结:解决较复杂的计算问题,通过画图可以帮助理解计算方法,使计算更直观、简单。1.画一画,填一填。
(1)按照规律画一画,如果这样画下去,第10个图形中有( )个点。
100(2)先观察下列图形的规律,再填空。
第6个图形一共由( )个小三角形组成,第n个图形一共由( )个小三角形组成。5736n2(3)我们可以从一角向外扩展来看找规律,再填空。
图(1):1=12
图(2):1+3=4=22
图(3):1+3+5=9=32
图(4):1+3+5+7= ( ) = ( ) 2
图(5): ( ) + ( ) + ( ) + ( ) + ( ) = ( ) = ( ) 2
……
我会用:1+3+5+7+9+11+13= ( ) 2
92=________________________________416571+3+5+7+9+11+13 + 15+17(4)看图找规律,再填空。
① 2=1×2
② 2+4=____×____
③ 2+4+6=____×____
④ 2+4+6+8=____×____
根据上面的规律写一写。
2+4+6+8+10=____×____=______
2+4+6+8+10+12+14+16=____×____=______30722.算一算,填一填。(1)一条马路长200 m,小亮和他的小狗分别以均匀的速度同时从马路的起点出发。当小亮走到这条马路一半的时候,小狗已经到达马路的终点。然后小狗返回与小亮相向而行,遇到小亮以后再跑向终点,到达终点以后再与小亮相向而行……直到小亮到达终点。小狗从出发开始,一共跑了多少米?3.解决问题狗的速度是人的速度的2倍起点终点 200×2=400( 米)答:小狗从出发开始,一共跑了400米。(2)小林、小强、小芳、小兵和小刚5 人进行象棋 比赛,每2 人之间都要下一盘。小林已经下了4盘,小强下了3盘,小芳下了2 盘,
小兵下了1 盘。请问:
小刚一共下了几盘?
分别和谁下的?
(选题源于教材P111第6题)答:小刚一共下了2盘,分别和小林、小强。小刚小林小强小芳小兵43用连线的方法试试。(点击人名)122(3)(3)我国宋代数学家杨辉在公元1261年撰写了《详解九章算法》,他在这本著作中画了一个由数构成的三角形图,我们把它称为“杨辉三角”。你能发现右面“杨辉三角”图中各数之间的关系吗?你能按照发现的规律把这个三角形表继续写下去吗?试试看。(选题源于教材P111练习二十二第7题) 答案略。(4)你能利用右面的图发现 这一公式吗?利用你所学的面积计算的知识,探索一下。(选题源于教材P111练习二十二第8题) 1. 从1开始的连续奇数的和正好是这串数个数的平方。
2. 有些计算问题或较为复杂的题目可以通过画图,把数字、算式转化成图形,使复杂的问题简单化、抽象的问题直观化,解决起来会更直观、更简单。数与形:作 业 请完成教材第108页“做一做” 第2题,第109页练习二十二第2题、第3题、第5题。 Thank you!
5+3+1= 32 42+ 32 =25
251+3+5+7+9+11+13+11+9+7+5+3+1=( )85下面每个图中最外圈有多少个小正方形?
(选题源于教材P109第1题)照这样画下去,第5个图形最外圈有( )个小正方形。4032 -1= 852 -32 = 1672 -52 = 24112 -92 = 40?初步感受极限思想例2 在这列数中,你能发现什么规律? 从第二个数开始,每个数是前一个数的 。 计算 算一算、猜一猜,结果可能是多少?然后借助线段图或圆形图来帮助思考,验证你的猜测是否正确? ……加下去,等号右边的分数越来越接近于1。计算。线段图理解 有些问题通过画图,解决起来更直观、容易。 计算 1计算。圆形图理解 …… 先在图形上表示出 ,再表示出 , , 等,并不断地累加下去,其结果越来越接近1。当这个过程无止境地持续下去时,相加之和为1,这种数学思考方式体现了极限思想。 极限思想如上图所示: 的和等于单位“1”减去最后一个小正方形的面积,即 。除了借助线段图和圆形图进行理解,我们还可以用什么图形表示单位“1”呢?想一想:用一个正方形表示单位“1”:归纳总结:解决较复杂的计算问题,通过画图可以帮助理解计算方法,使计算更直观、简单。1.画一画,填一填。
(1)按照规律画一画,如果这样画下去,第10个图形中有( )个点。
100(2)先观察下列图形的规律,再填空。
第6个图形一共由( )个小三角形组成,第n个图形一共由( )个小三角形组成。5736n2(3)我们可以从一角向外扩展来看找规律,再填空。
图(1):1=12
图(2):1+3=4=22
图(3):1+3+5=9=32
图(4):1+3+5+7= ( ) = ( ) 2
图(5): ( ) + ( ) + ( ) + ( ) + ( ) = ( ) = ( ) 2
……
我会用:1+3+5+7+9+11+13= ( ) 2
92=________________________________416571+3+5+7+9+11+13 + 15+17(4)看图找规律,再填空。
① 2=1×2
② 2+4=____×____
③ 2+4+6=____×____
④ 2+4+6+8=____×____
根据上面的规律写一写。
2+4+6+8+10=____×____=______
2+4+6+8+10+12+14+16=____×____=______30722.算一算,填一填。(1)一条马路长200 m,小亮和他的小狗分别以均匀的速度同时从马路的起点出发。当小亮走到这条马路一半的时候,小狗已经到达马路的终点。然后小狗返回与小亮相向而行,遇到小亮以后再跑向终点,到达终点以后再与小亮相向而行……直到小亮到达终点。小狗从出发开始,一共跑了多少米?3.解决问题狗的速度是人的速度的2倍起点终点 200×2=400( 米)答:小狗从出发开始,一共跑了400米。(2)小林、小强、小芳、小兵和小刚5 人进行象棋 比赛,每2 人之间都要下一盘。小林已经下了4盘,小强下了3盘,小芳下了2 盘,
小兵下了1 盘。请问:
小刚一共下了几盘?
分别和谁下的?
(选题源于教材P111第6题)答:小刚一共下了2盘,分别和小林、小强。小刚小林小强小芳小兵43用连线的方法试试。(点击人名)122(3)(3)我国宋代数学家杨辉在公元1261年撰写了《详解九章算法》,他在这本著作中画了一个由数构成的三角形图,我们把它称为“杨辉三角”。你能发现右面“杨辉三角”图中各数之间的关系吗?你能按照发现的规律把这个三角形表继续写下去吗?试试看。(选题源于教材P111练习二十二第7题) 答案略。(4)你能利用右面的图发现 这一公式吗?利用你所学的面积计算的知识,探索一下。(选题源于教材P111练习二十二第8题) 1. 从1开始的连续奇数的和正好是这串数个数的平方。
2. 有些计算问题或较为复杂的题目可以通过画图,把数字、算式转化成图形,使复杂的问题简单化、抽象的问题直观化,解决起来会更直观、更简单。数与形:作 业 请完成教材第108页“做一做” 第2题,第109页练习二十二第2题、第3题、第5题。 Thank you!
