23.6.1 用坐标确定位置课时作业
图片预览



文档简介
23.6.1 用坐标确定位置课时作业
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.以边长为的正方形的对角线建立平面直角坐标系,其中一个顶点位于轴的负半轴上,则该点的坐标为( )
A. B. C. D.
2.如图,△AOB关于x轴对称图形△A′OB,若△AOB内任意一点P的坐标是(a,b),则△A′OB中的对应点Q的坐标是( )
A. (a,b) B. (﹣a,b) C. (﹣a,﹣b) D. (a,﹣b)
3.如图是小强画出的一张脸的简笔画,他对小刚说:“我用(0,2)表示左眼的位置,用(2,2)表示右眼的位置”,那么嘴的位置可表示成( )
A. (1,0) B. (﹣1,0) C. (0,1) D. (1,﹣1)
4.如图,象棋盘上,若“帅”位于点,“马”位于点,则“炮”位于点
A. B. C. D.
5.体育课上,七年级某班49名同学在操场上练习正方形方队,他们站成7×7方队,每横队7人,每纵队7人,小敏在第2纵队的排头,记为(1,2),小娟在第5纵队的队尾,则小娟的位置应记为( )
A. (6,5) B. (5,6) C. (5,7) D. (7,5)
6.(龙口市校级期中)小敏的家在学校正南方向150 m,正东方向200 m处,如果以学校位置为原点,以正北、正东为正方向,则小敏家用有序数对(规定:东西方向在前,南北方向在后)表示为( )
A. (-200,-150) B. (200,150)
C. (200,-150) D. (-200,150)
7.下列几种说法:①北纬30°,东经115°;②海口的南面;③第1排第4列.其中能确定位置的有( )
A. 0个 B. 1个 C. 2个 D. 3个
8.如图,如果四角星的顶点A的位置用(5,8)表示,那么顶点B的位置可以表示为( )
A. (2,5) B. (5,2) C. (3,5) D. (5,3)
二、填空题
9.如图,A表示三经路与一纬路的十字路口,B表示一经路与三纬路的十字路口,如果用(3,1)?(3,2)?(3,3)?(2,3)?(1,3)表示由A到B的一条路径,用同样的方式写出一条由A到B的路径:____________________.
10.下列语句:①11排6号;②解放路112号;③南偏东36°;④东经118°,北纬40°.其中能确定物体具体位置的是__________(填序号).
11.如图是一组密码的一部分,请你运用所学知识找到破译的“钥匙”.目前,已破译出“正做数学”的真实意思是“祝你成功”.若“正”所处的位置为(x,y),你找到的密码钥匙是:横坐标_____,纵坐标_____,破译的“今天考试”真实意思是_____.
12.如图是某植物园的平面图,图中A馆所在地用坐标表示为(1,0),B馆所在地用坐标表示为(-3,-1),那么C馆所在地用坐标表示为_______.
13.如下图,围棋盘的左下角呈现的是一局围棋比赛中的几手棋,为记录棋谱方便,横 线用数字表示,纵线用英文字母表示,这样白棋②的位置可记为(E,3),则白棋⑥的位置 应记为________.
14.如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2;再向正东方向走6m到达点A3;再向正南方向走8m到达点A4;再向正西方向走10m到达点A5;…,按如此规律走下去,当机器人走到点A2017时,点A2017的坐标为________.
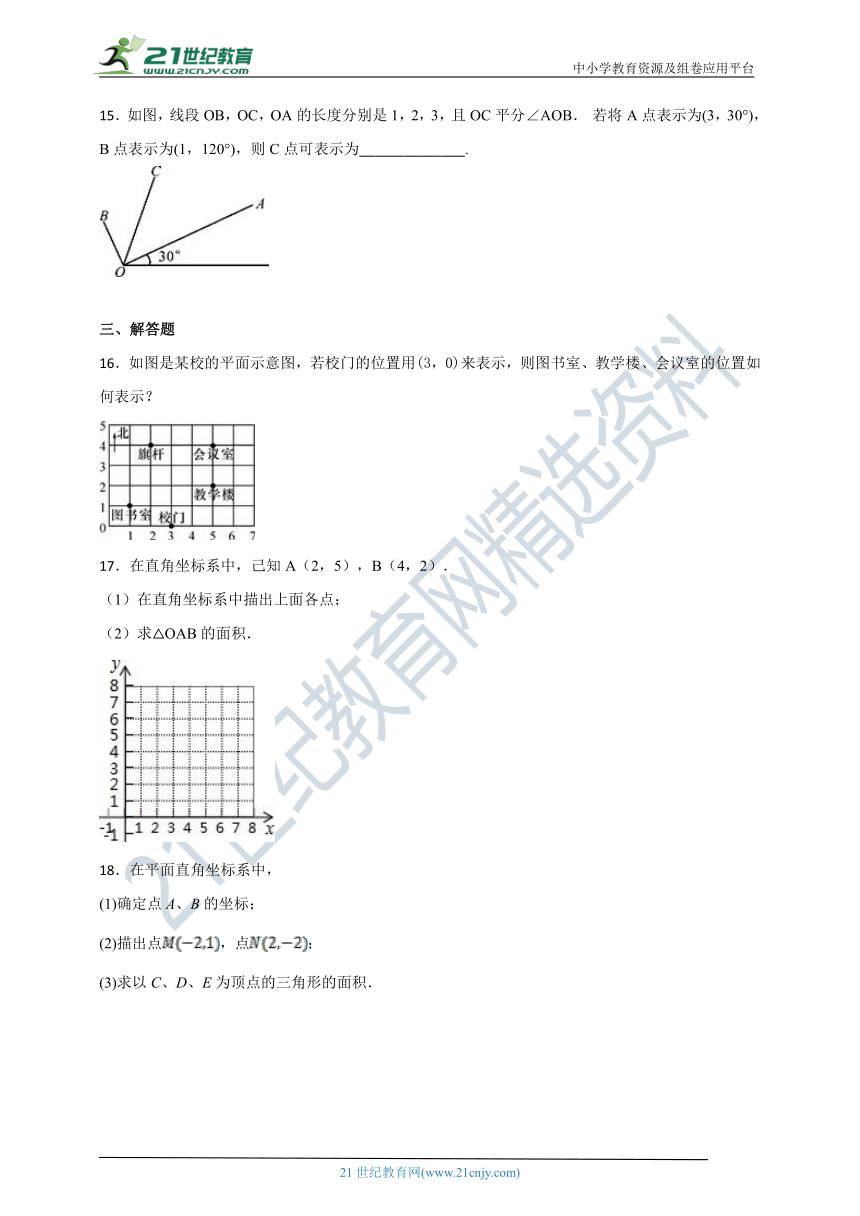
15.如图,线段OB,OC,OA的长度分别是1,2,3,且OC平分∠AOB. 若将A点表示为(3,30°),B点表示为(1,120°),则C点可表示为______________.
三、解答题
16.如图是某校的平面示意图,若校门的位置用(3,0)来表示,则图书室、教学楼、会议室的位置如何表示?
17.在直角坐标系中,己知A(2,5),B(4,2).
(1)在直角坐标系中描出上面各点;
(2)求△OAB的面积.
18.在平面直角坐标系中,
(1)确定点A、B的坐标;
(2)描出点,点;
(3)求以C、D、E为顶点的三角形的面积.
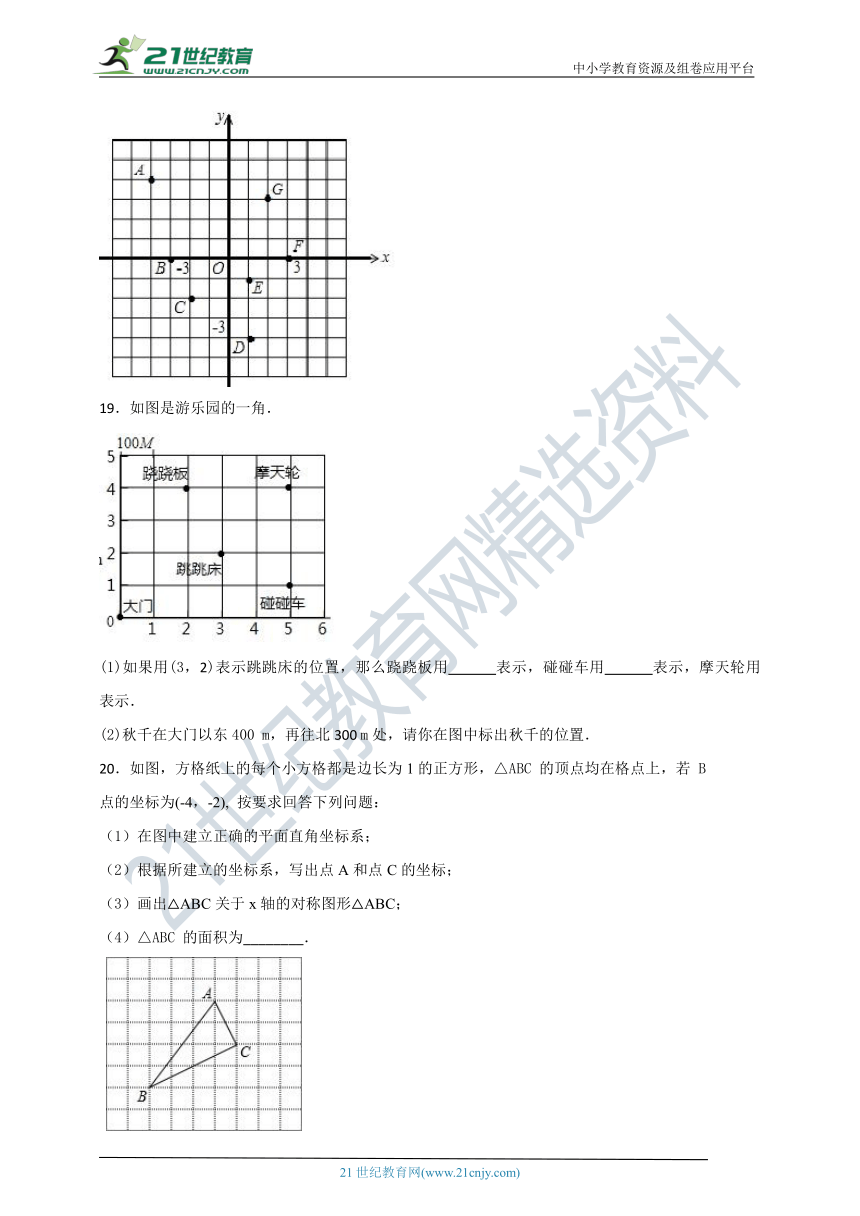
19.如图是游乐园的一角.
(1)如果用(3,2)表示跳跳床的位置,那么跷跷板用 表示,碰碰车用 表示,摩天轮用 表示.
(2)秋千在大门以东400 m,再往北300 m处,请你在图中标出秋千的位置.
20.如图,方格纸上的每个小方格都是边长为1的正方形,△ABC 的顶点均在格点上,若 B
点的坐标为(-4,-2), 按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点A和点C的坐标;
(3)画出△ABC关于x轴的对称图形△ABC;
(4)△ABC 的面积为________.
21.如图,已知△ABC在平面直角坐标系中的位置如图所示:
(1)写出△ABC三个顶点的坐标;
(2)在图中画出把△ABC先向左平移5个单位,再向上平移2个单位后所得的△A′B′C′,并写出它的各顶点坐标.
(3)求出△ABC的面积;
参考答案
1.D
【解析】
【分析】
根据正方形的对角线等于边长的倍求出对角线的长度,再根据正方形的对角线互相平分求出顶点到原点的距离,然后根据y轴上的点的坐标特征解答即可.
【详解】
∵正方形的边长是4, ∴正方形的对角线是4, ∵正方形的对角线互相平分, ∴顶点到原点的距离为2, ∴位于y轴的负半轴上的点的坐标为(0,-2). 故选:D.
【点睛】
考查了坐标与图形的性质,主要利用了正方形的对角线与边长的关系,正方形的对角线互相平分,以及坐标轴上的点的坐标特征.
2.D
【解析】
【分析】
根据关于x轴对称的点的横坐标相同,纵坐标互为相反数解答即可.
【详解】
∵△AOB与△A'OB关于x轴对称,
∴点P(a,b)关于x轴的对称点为(a,-b),
∴点P的对应点Q的坐标是(a,-b).
故选D.
【点睛】
本题考查了坐标与图形变化-对称,熟记关于x轴对称的点的横坐标相同,纵坐标互为相反数是解题的关键.
3.A
【解析】分析:根据(0,2)表示左眼确定原点的位置和单位长度,得到嘴的位置.
详解:因为(0,2)表示左眼,所以原点在左眼的下方2个单位长度,则嘴的位置是(1,0).
故选A.
点睛:根据已知点的位置和坐标确定坐标系的原点和单位长度,从而得到目标点的坐标.
4.B
【解析】
【分析】
利用已知点位置建立平面直角坐标系,进而得出答案.
【详解】
如图所示:“炮”位于点:.
故选:B.
【点睛】
此题主要考查了坐标确定位置,正确得出原点位置是解题关键.
5.D
【解析】试题解析:由题意知,横行数在前,纵列数在后,小娟是第5纵队的队尾,即为第7横行第5纵列,所以应记为
故选D.
6.C
【解析】小敏家用有序数对表示为(200,-150).
故选C.
点睛:掌握有序数对的表示方法.
7.C
【解析】根据有序数对的含义,可知位置的确定需要两个不同的数,所以①、③能确定位置,而②只能确定方向,不能确定位置.
故选:C.
8.A
【解析】根据题意,可知各点的未知表示为(纵线数,横线数),因此可知点B的位置可表示为(2,5).
故选:A.
点睛:此题主要考查了有序数对表示位置的方法,关键是根据题意中的位置表示确定出点的位置的规律,然后以此规律表示即可.
9.(3,1)→(2,1)→(2,2)→(2,3)→(1,3)
【解析】根据题意明确:横坐标表示经路,纵坐标表示纬路.然后结合图形画出路线,写出对应的坐标即可:一条由A到B的路径(3,1)→(2,1)→(2,2)→(2,3)→(1,3).
故答案是:(3,1)→(2,1)→(2,2)→(2,3)→(1,3).
10.①②④
【解析】①在电影院内,相当于在平面直角坐标系内,确定一个座位需要2个数据,一个用来确定排,一个用来确定号;②在一定范围内,相当于在平面直角坐标系内,确定一个地址需要2个数据,一个用来确定路,一个用来确定号;③南偏东36°,只有方位,没有距离,故不能确定位置;④东经118°,北纬40°,经纬度从两个方面确定了物体的具体位置.故答案为①②④.
11. 加1, 加2, 努力发挥.
【解析】
【分析】
通过分析比较“正做数学”与“祝你成功”坐标之间的关系,进而确定“密码钥匙”为(x+1,y+2),据此解答即可.
【详解】
∵正、做、数、学四个字的位置分别为(4,2)、(5,6)、(7,2)、(2,4),
祝、你、成、功四个字所在位置是(5,4)、(6,8)、(8,4)、(3,6),
∴密码钥匙是:横坐标加1,纵坐标加2,
∵今、天、考、试四个字的位置分别为(3,2)、(5,1)、(1,5)、(6,6),
∴真实意思的四个字所在位置是(4,4)、(6,3)、(2,7)、(7,8),
∴“今天考试”的真实意思是“努力发挥”.
故答案为:加1, 加2,努力发挥.
【点睛】
此题属于探究规律类型的题目,考查了用有序数对表示物体的位置,通过解答此题,要求同学们学会简单的归纳.解答本题的关键是根据题意确定“密码钥匙”, 解答本题的关键是找出破译前与破译后各个字坐标之间的规律.
12.(2,4)
【解析】建立平面直角坐标系如图所示:
则C馆所在地用坐标表示为(2,4),
故答案为:(2,4).
13.(G,5)
【解析】白棋⑥的位置可以看做白棋②的位置可记为(E,3)向右平移2个单位,再向上平移2个单位得到: (G,5).
故答案:(G,5).
14.(﹣2018,﹣2016)
【解析】解:观察图象可知,下标为偶数时在二四象限,下标为奇数时在一三象限,除以4余数是3的在第一象限,除以4余数是1的在第三象限,因为2017=504×4+1,所以A2017在第三象限.∵A1(-2,0),A5(-6,-4),A9(-10,-8),∴A2017坐标为(﹣2018,﹣2016).故答案为:(﹣2018,﹣2016).
点睛:本题考查了了规律型:点的坐标问题,解题的关键是发现规律,利用规律解决问题,本题的突破点是判定A2017在第三象限,属于中考常考题型.
15.(2,75°)
【解析】试题解析::∵线段OB、OC、OA的长度分别是1、2、3,且OC平分∠AOB.若将A点表示为(3,30°),B点表示为(1,120°),
∴∠AOB=90°,∠AOC=45°,
则C点可表示为(2,75°).
故答案为:(2,75°).
16.图书室(1,1),教学楼(5,2),会议室(5,4)
【解析】试题分析:
根据校门的坐标确定原点的位置,然后再来求解.
试题解析:
图书室(1,1),教学楼(5,2),会议室(5,4)
17.(1)见解析;(2)8
【解析】试题分析:(1)描点, (2)利用长方形面积减去三个直角三角形面积差求.
试题解析:
(1)如图所示:
(2)S△OAB=
=20-5-3-4
=8.
18.(1) ,;(2)作图见解析;(3).
【解析】
【分析】
(1)根据方格纸中建立的坐标系确定出点A、B的坐标即可;
(2)根据M、N的坐标在图中的坐标系里描出表示这两个点的点即可;
(3)顺次连接C、D、E三点后可知,DE=3,DE边上的高为3,由此即可由三角形的面积公式计算出△CDE的面积了.
【详解】
(1)如图所示:点A的坐标为(-4,4),点B的坐标为(-3,0);
(2)按要求在坐标系中描出表示M(-2,1)和N(2,-2)如下图所示:
(3)如上图所示:
△CDE中,DE=3,DE边上的高为3,
∴S△CDE=.
【点睛】
熟知“(1)在平面直角坐标系中根据点的位置确定点的坐标的方法;(2)由点的坐标描出点在平面直角坐标系中的位置的方法”是解答本题的关键.
19.(1)(2,4),(5,1),(5,4)(2)图形见解析
【解析】试题分析:(1)根据有序数对的定义,因为(3,2)表示跳跳床的位置,其中3是第3列,2是第2行,则对于任一数对(a,b),a表示第a列,b表示第b行;
(2)图中一格代表100m,则向东400m即向东4格,向北300m即向北3格,根据网格结构找出秋千的位置标注即可.
试题解析:(1) 跷跷板在第2列,第4行,则表示为(2,4);碰碰车在第5列,第1行,则表示为 (5,1);摩天轮在第5列,第4行,则表示为(5,4);
(2)标出秋千的位置如图所示:
20.5
【解析】
【分析】
(1)利用B点坐标即可得出原点位置进而得出坐标轴的位置;
(2)利用平面坐标系得出点A和点C的坐标;
(3)利用关于x轴对称点的性质,得出对应点坐标进而得出答案;
(4)利用矩形面积减去周围三角形面积即可得出△ABC的面积.
【详解】
(1)如图所示:
(2)点 A(﹣1,2),点 C(0,0);
(3)如图所示:△A′B′C′即为所求;
(4)△ABC 的面积为:16﹣×3×4﹣×1×2﹣×2×4=5.
故答案为:5.
【点睛】
此题主要考查了轴对称变换以及三角形面积求法和利用坐标确定位置,得出对应点坐标是解题关键.
21.(1) A(4, 3),B(3, 1),C(1, 2);(2) A′ (-1, 5),B′( -2, 3),C′(-4, 4);(3)S△ABC=
【解析】【分析】(1)根据图写出坐标;(2)先画出图,再写坐标;(3)由图形面积减去两个三角形面积即可.
【详解】解:(1) A(4, 3),B(3, 1),C(1, 2);
(2) 如图;
A′ (-1, 5),B′( -2, 3),C′(-4, 4);
(3)S△ABC=(1+2) ×3 -1×2×-1×2×=
【点睛】本题考核知识点:平移,平面直角坐标系. 解题关键点:理解点的坐标的意义.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.以边长为的正方形的对角线建立平面直角坐标系,其中一个顶点位于轴的负半轴上,则该点的坐标为( )
A. B. C. D.
2.如图,△AOB关于x轴对称图形△A′OB,若△AOB内任意一点P的坐标是(a,b),则△A′OB中的对应点Q的坐标是( )
A. (a,b) B. (﹣a,b) C. (﹣a,﹣b) D. (a,﹣b)
3.如图是小强画出的一张脸的简笔画,他对小刚说:“我用(0,2)表示左眼的位置,用(2,2)表示右眼的位置”,那么嘴的位置可表示成( )
A. (1,0) B. (﹣1,0) C. (0,1) D. (1,﹣1)
4.如图,象棋盘上,若“帅”位于点,“马”位于点,则“炮”位于点
A. B. C. D.
5.体育课上,七年级某班49名同学在操场上练习正方形方队,他们站成7×7方队,每横队7人,每纵队7人,小敏在第2纵队的排头,记为(1,2),小娟在第5纵队的队尾,则小娟的位置应记为( )
A. (6,5) B. (5,6) C. (5,7) D. (7,5)
6.(龙口市校级期中)小敏的家在学校正南方向150 m,正东方向200 m处,如果以学校位置为原点,以正北、正东为正方向,则小敏家用有序数对(规定:东西方向在前,南北方向在后)表示为( )
A. (-200,-150) B. (200,150)
C. (200,-150) D. (-200,150)
7.下列几种说法:①北纬30°,东经115°;②海口的南面;③第1排第4列.其中能确定位置的有( )
A. 0个 B. 1个 C. 2个 D. 3个
8.如图,如果四角星的顶点A的位置用(5,8)表示,那么顶点B的位置可以表示为( )
A. (2,5) B. (5,2) C. (3,5) D. (5,3)
二、填空题
9.如图,A表示三经路与一纬路的十字路口,B表示一经路与三纬路的十字路口,如果用(3,1)?(3,2)?(3,3)?(2,3)?(1,3)表示由A到B的一条路径,用同样的方式写出一条由A到B的路径:____________________.
10.下列语句:①11排6号;②解放路112号;③南偏东36°;④东经118°,北纬40°.其中能确定物体具体位置的是__________(填序号).
11.如图是一组密码的一部分,请你运用所学知识找到破译的“钥匙”.目前,已破译出“正做数学”的真实意思是“祝你成功”.若“正”所处的位置为(x,y),你找到的密码钥匙是:横坐标_____,纵坐标_____,破译的“今天考试”真实意思是_____.
12.如图是某植物园的平面图,图中A馆所在地用坐标表示为(1,0),B馆所在地用坐标表示为(-3,-1),那么C馆所在地用坐标表示为_______.
13.如下图,围棋盘的左下角呈现的是一局围棋比赛中的几手棋,为记录棋谱方便,横 线用数字表示,纵线用英文字母表示,这样白棋②的位置可记为(E,3),则白棋⑥的位置 应记为________.
14.如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2;再向正东方向走6m到达点A3;再向正南方向走8m到达点A4;再向正西方向走10m到达点A5;…,按如此规律走下去,当机器人走到点A2017时,点A2017的坐标为________.
15.如图,线段OB,OC,OA的长度分别是1,2,3,且OC平分∠AOB. 若将A点表示为(3,30°),B点表示为(1,120°),则C点可表示为______________.
三、解答题
16.如图是某校的平面示意图,若校门的位置用(3,0)来表示,则图书室、教学楼、会议室的位置如何表示?
17.在直角坐标系中,己知A(2,5),B(4,2).
(1)在直角坐标系中描出上面各点;
(2)求△OAB的面积.
18.在平面直角坐标系中,
(1)确定点A、B的坐标;
(2)描出点,点;
(3)求以C、D、E为顶点的三角形的面积.
19.如图是游乐园的一角.
(1)如果用(3,2)表示跳跳床的位置,那么跷跷板用 表示,碰碰车用 表示,摩天轮用 表示.
(2)秋千在大门以东400 m,再往北300 m处,请你在图中标出秋千的位置.
20.如图,方格纸上的每个小方格都是边长为1的正方形,△ABC 的顶点均在格点上,若 B
点的坐标为(-4,-2), 按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点A和点C的坐标;
(3)画出△ABC关于x轴的对称图形△ABC;
(4)△ABC 的面积为________.
21.如图,已知△ABC在平面直角坐标系中的位置如图所示:
(1)写出△ABC三个顶点的坐标;
(2)在图中画出把△ABC先向左平移5个单位,再向上平移2个单位后所得的△A′B′C′,并写出它的各顶点坐标.
(3)求出△ABC的面积;
参考答案
1.D
【解析】
【分析】
根据正方形的对角线等于边长的倍求出对角线的长度,再根据正方形的对角线互相平分求出顶点到原点的距离,然后根据y轴上的点的坐标特征解答即可.
【详解】
∵正方形的边长是4, ∴正方形的对角线是4, ∵正方形的对角线互相平分, ∴顶点到原点的距离为2, ∴位于y轴的负半轴上的点的坐标为(0,-2). 故选:D.
【点睛】
考查了坐标与图形的性质,主要利用了正方形的对角线与边长的关系,正方形的对角线互相平分,以及坐标轴上的点的坐标特征.
2.D
【解析】
【分析】
根据关于x轴对称的点的横坐标相同,纵坐标互为相反数解答即可.
【详解】
∵△AOB与△A'OB关于x轴对称,
∴点P(a,b)关于x轴的对称点为(a,-b),
∴点P的对应点Q的坐标是(a,-b).
故选D.
【点睛】
本题考查了坐标与图形变化-对称,熟记关于x轴对称的点的横坐标相同,纵坐标互为相反数是解题的关键.
3.A
【解析】分析:根据(0,2)表示左眼确定原点的位置和单位长度,得到嘴的位置.
详解:因为(0,2)表示左眼,所以原点在左眼的下方2个单位长度,则嘴的位置是(1,0).
故选A.
点睛:根据已知点的位置和坐标确定坐标系的原点和单位长度,从而得到目标点的坐标.
4.B
【解析】
【分析】
利用已知点位置建立平面直角坐标系,进而得出答案.
【详解】
如图所示:“炮”位于点:.
故选:B.
【点睛】
此题主要考查了坐标确定位置,正确得出原点位置是解题关键.
5.D
【解析】试题解析:由题意知,横行数在前,纵列数在后,小娟是第5纵队的队尾,即为第7横行第5纵列,所以应记为
故选D.
6.C
【解析】小敏家用有序数对表示为(200,-150).
故选C.
点睛:掌握有序数对的表示方法.
7.C
【解析】根据有序数对的含义,可知位置的确定需要两个不同的数,所以①、③能确定位置,而②只能确定方向,不能确定位置.
故选:C.
8.A
【解析】根据题意,可知各点的未知表示为(纵线数,横线数),因此可知点B的位置可表示为(2,5).
故选:A.
点睛:此题主要考查了有序数对表示位置的方法,关键是根据题意中的位置表示确定出点的位置的规律,然后以此规律表示即可.
9.(3,1)→(2,1)→(2,2)→(2,3)→(1,3)
【解析】根据题意明确:横坐标表示经路,纵坐标表示纬路.然后结合图形画出路线,写出对应的坐标即可:一条由A到B的路径(3,1)→(2,1)→(2,2)→(2,3)→(1,3).
故答案是:(3,1)→(2,1)→(2,2)→(2,3)→(1,3).
10.①②④
【解析】①在电影院内,相当于在平面直角坐标系内,确定一个座位需要2个数据,一个用来确定排,一个用来确定号;②在一定范围内,相当于在平面直角坐标系内,确定一个地址需要2个数据,一个用来确定路,一个用来确定号;③南偏东36°,只有方位,没有距离,故不能确定位置;④东经118°,北纬40°,经纬度从两个方面确定了物体的具体位置.故答案为①②④.
11. 加1, 加2, 努力发挥.
【解析】
【分析】
通过分析比较“正做数学”与“祝你成功”坐标之间的关系,进而确定“密码钥匙”为(x+1,y+2),据此解答即可.
【详解】
∵正、做、数、学四个字的位置分别为(4,2)、(5,6)、(7,2)、(2,4),
祝、你、成、功四个字所在位置是(5,4)、(6,8)、(8,4)、(3,6),
∴密码钥匙是:横坐标加1,纵坐标加2,
∵今、天、考、试四个字的位置分别为(3,2)、(5,1)、(1,5)、(6,6),
∴真实意思的四个字所在位置是(4,4)、(6,3)、(2,7)、(7,8),
∴“今天考试”的真实意思是“努力发挥”.
故答案为:加1, 加2,努力发挥.
【点睛】
此题属于探究规律类型的题目,考查了用有序数对表示物体的位置,通过解答此题,要求同学们学会简单的归纳.解答本题的关键是根据题意确定“密码钥匙”, 解答本题的关键是找出破译前与破译后各个字坐标之间的规律.
12.(2,4)
【解析】建立平面直角坐标系如图所示:
则C馆所在地用坐标表示为(2,4),
故答案为:(2,4).
13.(G,5)
【解析】白棋⑥的位置可以看做白棋②的位置可记为(E,3)向右平移2个单位,再向上平移2个单位得到: (G,5).
故答案:(G,5).
14.(﹣2018,﹣2016)
【解析】解:观察图象可知,下标为偶数时在二四象限,下标为奇数时在一三象限,除以4余数是3的在第一象限,除以4余数是1的在第三象限,因为2017=504×4+1,所以A2017在第三象限.∵A1(-2,0),A5(-6,-4),A9(-10,-8),∴A2017坐标为(﹣2018,﹣2016).故答案为:(﹣2018,﹣2016).
点睛:本题考查了了规律型:点的坐标问题,解题的关键是发现规律,利用规律解决问题,本题的突破点是判定A2017在第三象限,属于中考常考题型.
15.(2,75°)
【解析】试题解析::∵线段OB、OC、OA的长度分别是1、2、3,且OC平分∠AOB.若将A点表示为(3,30°),B点表示为(1,120°),
∴∠AOB=90°,∠AOC=45°,
则C点可表示为(2,75°).
故答案为:(2,75°).
16.图书室(1,1),教学楼(5,2),会议室(5,4)
【解析】试题分析:
根据校门的坐标确定原点的位置,然后再来求解.
试题解析:
图书室(1,1),教学楼(5,2),会议室(5,4)
17.(1)见解析;(2)8
【解析】试题分析:(1)描点, (2)利用长方形面积减去三个直角三角形面积差求.
试题解析:
(1)如图所示:
(2)S△OAB=
=20-5-3-4
=8.
18.(1) ,;(2)作图见解析;(3).
【解析】
【分析】
(1)根据方格纸中建立的坐标系确定出点A、B的坐标即可;
(2)根据M、N的坐标在图中的坐标系里描出表示这两个点的点即可;
(3)顺次连接C、D、E三点后可知,DE=3,DE边上的高为3,由此即可由三角形的面积公式计算出△CDE的面积了.
【详解】
(1)如图所示:点A的坐标为(-4,4),点B的坐标为(-3,0);
(2)按要求在坐标系中描出表示M(-2,1)和N(2,-2)如下图所示:
(3)如上图所示:
△CDE中,DE=3,DE边上的高为3,
∴S△CDE=.
【点睛】
熟知“(1)在平面直角坐标系中根据点的位置确定点的坐标的方法;(2)由点的坐标描出点在平面直角坐标系中的位置的方法”是解答本题的关键.
19.(1)(2,4),(5,1),(5,4)(2)图形见解析
【解析】试题分析:(1)根据有序数对的定义,因为(3,2)表示跳跳床的位置,其中3是第3列,2是第2行,则对于任一数对(a,b),a表示第a列,b表示第b行;
(2)图中一格代表100m,则向东400m即向东4格,向北300m即向北3格,根据网格结构找出秋千的位置标注即可.
试题解析:(1) 跷跷板在第2列,第4行,则表示为(2,4);碰碰车在第5列,第1行,则表示为 (5,1);摩天轮在第5列,第4行,则表示为(5,4);
(2)标出秋千的位置如图所示:
20.5
【解析】
【分析】
(1)利用B点坐标即可得出原点位置进而得出坐标轴的位置;
(2)利用平面坐标系得出点A和点C的坐标;
(3)利用关于x轴对称点的性质,得出对应点坐标进而得出答案;
(4)利用矩形面积减去周围三角形面积即可得出△ABC的面积.
【详解】
(1)如图所示:
(2)点 A(﹣1,2),点 C(0,0);
(3)如图所示:△A′B′C′即为所求;
(4)△ABC 的面积为:16﹣×3×4﹣×1×2﹣×2×4=5.
故答案为:5.
【点睛】
此题主要考查了轴对称变换以及三角形面积求法和利用坐标确定位置,得出对应点坐标是解题关键.
21.(1) A(4, 3),B(3, 1),C(1, 2);(2) A′ (-1, 5),B′( -2, 3),C′(-4, 4);(3)S△ABC=
【解析】【分析】(1)根据图写出坐标;(2)先画出图,再写坐标;(3)由图形面积减去两个三角形面积即可.
【详解】解:(1) A(4, 3),B(3, 1),C(1, 2);
(2) 如图;
A′ (-1, 5),B′( -2, 3),C′(-4, 4);
(3)S△ABC=(1+2) ×3 -1×2×-1×2×=
【点睛】本题考核知识点:平移,平面直角坐标系. 解题关键点:理解点的坐标的意义.
