第三章 数据的分析章末小结
图片预览
文档简介
第三章 数据的分析 章末小结
知识构建
数据的分析:
一、数据的集中趋势:
1.平均数:(1)算术平均数: =①
(2) 加权平均数:为了区分各个数的② 计算平均数时给每个数据一个权
2.中位数:数据按大小顺序排列,处于最③ 的一个数据(或两个数据的④ )
3.众数:一组数据中⑤ 最多的那个数据
二、数据的离散程度:
1. 极差:一组数据中⑥ 数据与⑦ 数据的差
2. 方差:S2=⑧
3. 标准差:方差的算术⑨
中考链接
1.(2018舟山)某班要从9名百米跑成绩各不相同的同学中选4名参加4×100米接力赛,而这9名同学只知道自己的成绩,要想让他们知道自己是否入选,老师只需公布他们成绩的( )
A.平均数 B.中位数 C.众数 D.方差
2.(2018衡阳)要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )
A.平均数 B.中位数 C.众数 D.方差
3.(2018上海)某校调查了20名男生某一周参加篮球运动的次数,调查结果如表所示.那么这20名男生该周参加篮球运动次数的平均数是( )
次数
2
3
4
5
人数
2
2
10
6
A.3次 B.3.5次 C.4次 D.4.5次
4.(2017宿迁)一组数据5,4,2,5,6的中位数是( )
A.5 B.4 C.2 D.6
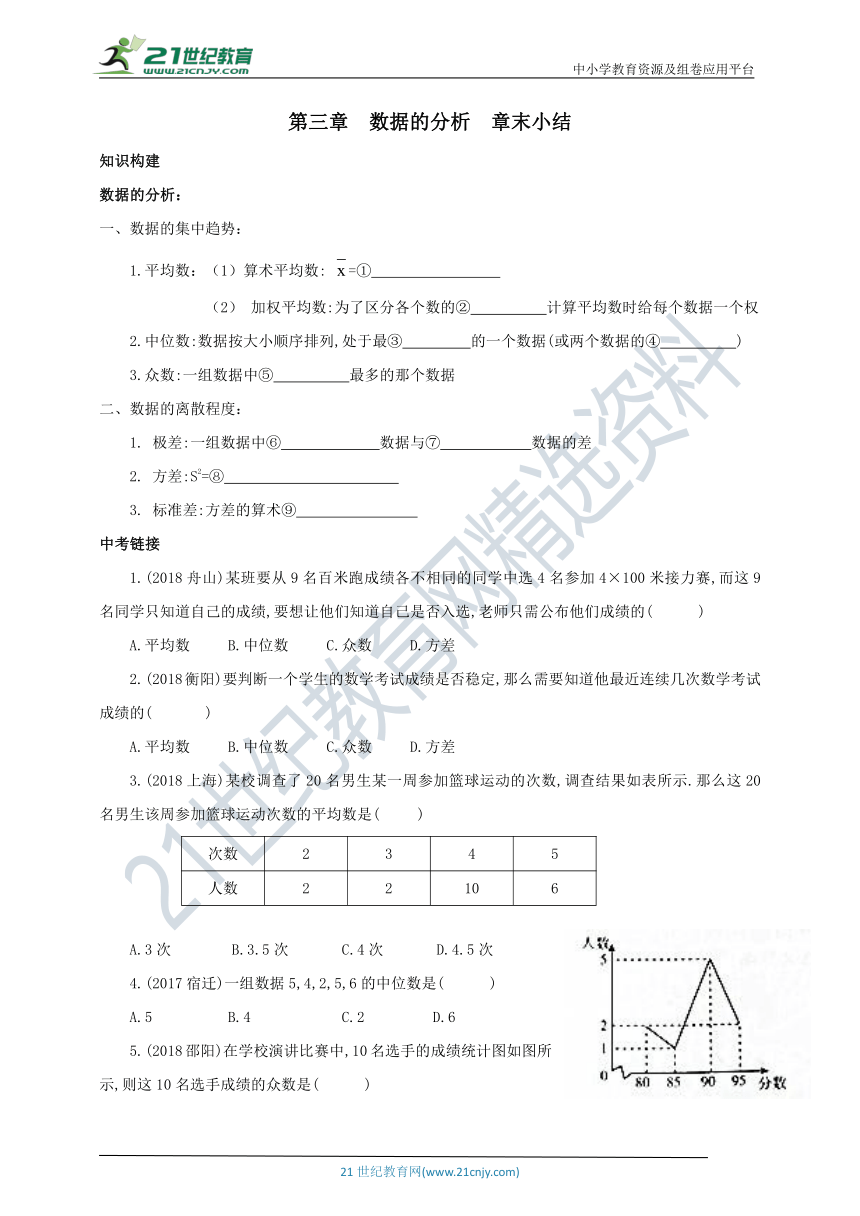
5.(2018邵阳)在学校演讲比赛中,10名选手的成绩统计图如图所示,则这10名选手成绩的众数是( )
A.95
B.90
C.85
D.80
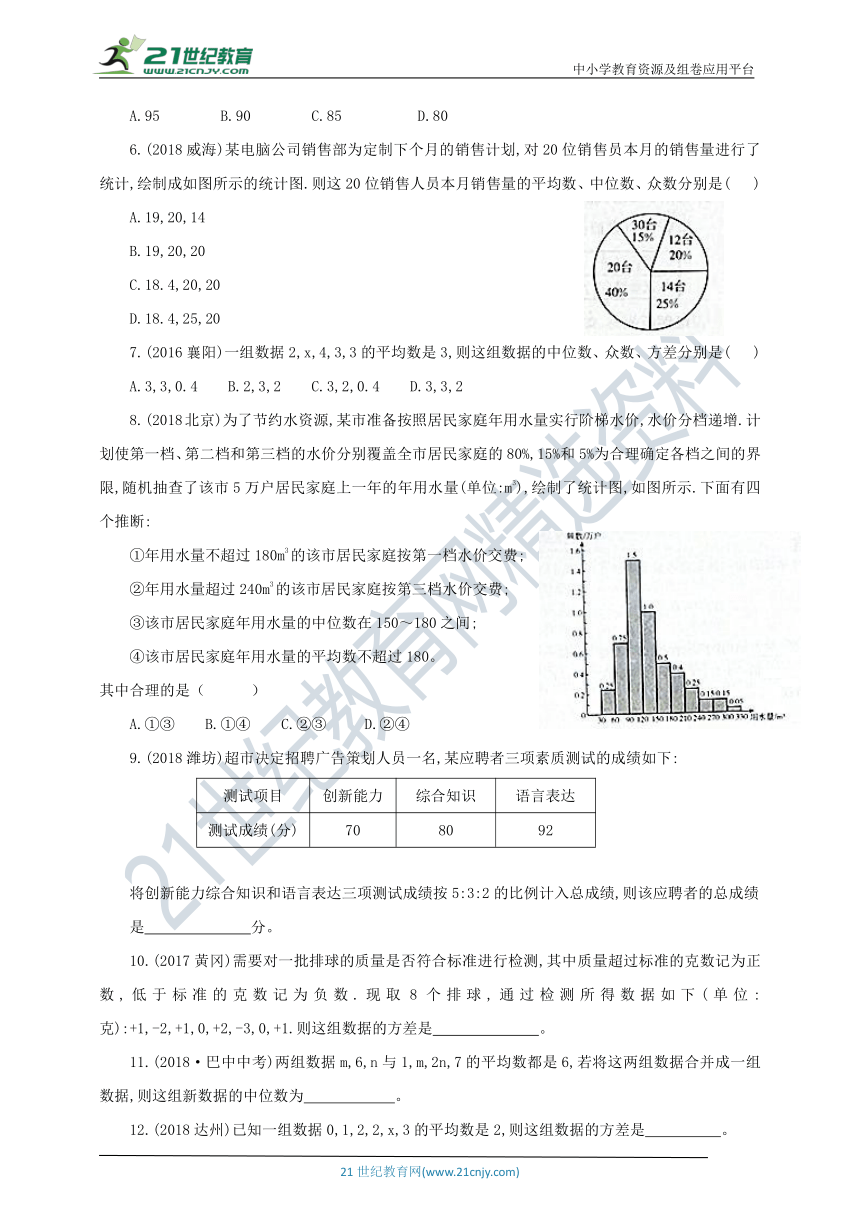
6.(2018威海)某电脑公司销售部为定制下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图.则这20位销售人员本月销售量的平均数、中位数、众数分别是( )
A.19,20,14
B.19,20,20
C.18.4,20,20
D.18.4,25,20
7.(2016襄阳)一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )
A.3,3,0.4 B.2,3,2 C.3,2,0.4 D.3,3,2
8.(2018北京)为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增.计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图,如图所示.下面有四个推断:
①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150~180之间;
④该市居民家庭年用水量的平均数不超过180。
其中合理的是( )
A.①③ B.①④ C.②③ D.②④
9.(2018潍坊)超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如下:
测试项目
创新能力
综合知识
语言表达
测试成绩(分)
70
80
92
将创新能力综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩
是 分。
10.(2017黃冈)需要对一批排球的质量是否符合标准进行检测,其中质量超过标准的克数记为正数,低于标准的克数记为负数.现取8个排球,通过检测所得数据如下(单位:克):+1,-2,+1,0,+2,-3,0,+1.则这组数据的方差是 。
11.(2018·巴中中考)两组数据m,6,n与1,m,2n,7的平均数都是6,若将这两组数据合并成一组数据,则这组新数据的中位数为 。
12.(2018达州)已知一组数据0,1,2,2,x,3的平均数是2,则这组数据的方差是 。
13.(2016广州)某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙、丙三个小组各项得分如下表:
小组
研究报告
小组展示
答辫
甲
91
80
78
乙
81
74
85
丙
79
83
90
计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%,计算各小组的成绩,哪个小组的
成绩最高?
14.(2018青岛)甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?请说明理由.
参考答案及解析
知识构建
①(x1+x2+…+xn) ②重要程度 ③中间位置
④平均数 ⑤出现次数 ⑥最大 ⑦最小
⑧[(x1-)2+(x2-)2+…+(xn-)2] ⑨平方根
中考链接
1.B 2.D 3.C 4.A 5.B 6.C 7.A 8.B 9.77.4 10.2.5 11.7 12.
13.解:(1)由题意可得,甲组的平均成绩是(91+80+78)÷3=83(分),
乙组的平均成绩是(81+74+85)÷3=80(分)
丙组的平均成绩是(79+83+90)÷3=84(分),
从高分到低分小组的排名顺序是:丙>甲>乙
(2)由题意可得,
甲组的平均成绩是( 91×40%+80×30%+78×30%)÷(40%+30%+30%) =83.8(分),
乙组的平均成绩是(81×40%+74×30%+85×30%)÷(40%+30%+30%)= 80.1(分),
丙组的平均成绩是(79×40%+83×30%+90×30%)÷(40%+30%+30%)= 83.5(分),
由上可得,甲组的成绩最高
14.解:(1)甲的平均成绩:a=(5×1+6×2+7×4+8×2+9×1)÷(1+2+4+2+1)=7(环)
∵乙的射击成绩从小到大排列为:3,4,6,7,7,8,8,8,9,10
∴乙射击成绩的中位数b=7+8=7.5(环),
乙的方差c=[(3-7)2+(4-7)2+(6-7)2+2(7-7)2+3×(8-7)2+(9-7)2+(10-7)2]=(16+9+1+3+4+9)
=4.2
(2)从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定.
综合以上各因素,若选派一名学生参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
知识构建
数据的分析:
一、数据的集中趋势:
1.平均数:(1)算术平均数: =①
(2) 加权平均数:为了区分各个数的② 计算平均数时给每个数据一个权
2.中位数:数据按大小顺序排列,处于最③ 的一个数据(或两个数据的④ )
3.众数:一组数据中⑤ 最多的那个数据
二、数据的离散程度:
1. 极差:一组数据中⑥ 数据与⑦ 数据的差
2. 方差:S2=⑧
3. 标准差:方差的算术⑨
中考链接
1.(2018舟山)某班要从9名百米跑成绩各不相同的同学中选4名参加4×100米接力赛,而这9名同学只知道自己的成绩,要想让他们知道自己是否入选,老师只需公布他们成绩的( )
A.平均数 B.中位数 C.众数 D.方差
2.(2018衡阳)要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )
A.平均数 B.中位数 C.众数 D.方差
3.(2018上海)某校调查了20名男生某一周参加篮球运动的次数,调查结果如表所示.那么这20名男生该周参加篮球运动次数的平均数是( )
次数
2
3
4
5
人数
2
2
10
6
A.3次 B.3.5次 C.4次 D.4.5次
4.(2017宿迁)一组数据5,4,2,5,6的中位数是( )
A.5 B.4 C.2 D.6
5.(2018邵阳)在学校演讲比赛中,10名选手的成绩统计图如图所示,则这10名选手成绩的众数是( )
A.95
B.90
C.85
D.80
6.(2018威海)某电脑公司销售部为定制下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图.则这20位销售人员本月销售量的平均数、中位数、众数分别是( )
A.19,20,14
B.19,20,20
C.18.4,20,20
D.18.4,25,20
7.(2016襄阳)一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )
A.3,3,0.4 B.2,3,2 C.3,2,0.4 D.3,3,2
8.(2018北京)为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增.计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图,如图所示.下面有四个推断:
①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150~180之间;
④该市居民家庭年用水量的平均数不超过180。
其中合理的是( )
A.①③ B.①④ C.②③ D.②④
9.(2018潍坊)超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如下:
测试项目
创新能力
综合知识
语言表达
测试成绩(分)
70
80
92
将创新能力综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩
是 分。
10.(2017黃冈)需要对一批排球的质量是否符合标准进行检测,其中质量超过标准的克数记为正数,低于标准的克数记为负数.现取8个排球,通过检测所得数据如下(单位:克):+1,-2,+1,0,+2,-3,0,+1.则这组数据的方差是 。
11.(2018·巴中中考)两组数据m,6,n与1,m,2n,7的平均数都是6,若将这两组数据合并成一组数据,则这组新数据的中位数为 。
12.(2018达州)已知一组数据0,1,2,2,x,3的平均数是2,则这组数据的方差是 。
13.(2016广州)某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙、丙三个小组各项得分如下表:
小组
研究报告
小组展示
答辫
甲
91
80
78
乙
81
74
85
丙
79
83
90
计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%,计算各小组的成绩,哪个小组的
成绩最高?
14.(2018青岛)甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?请说明理由.
参考答案及解析
知识构建
①(x1+x2+…+xn) ②重要程度 ③中间位置
④平均数 ⑤出现次数 ⑥最大 ⑦最小
⑧[(x1-)2+(x2-)2+…+(xn-)2] ⑨平方根
中考链接
1.B 2.D 3.C 4.A 5.B 6.C 7.A 8.B 9.77.4 10.2.5 11.7 12.
13.解:(1)由题意可得,甲组的平均成绩是(91+80+78)÷3=83(分),
乙组的平均成绩是(81+74+85)÷3=80(分)
丙组的平均成绩是(79+83+90)÷3=84(分),
从高分到低分小组的排名顺序是:丙>甲>乙
(2)由题意可得,
甲组的平均成绩是( 91×40%+80×30%+78×30%)÷(40%+30%+30%) =83.8(分),
乙组的平均成绩是(81×40%+74×30%+85×30%)÷(40%+30%+30%)= 80.1(分),
丙组的平均成绩是(79×40%+83×30%+90×30%)÷(40%+30%+30%)= 83.5(分),
由上可得,甲组的成绩最高
14.解:(1)甲的平均成绩:a=(5×1+6×2+7×4+8×2+9×1)÷(1+2+4+2+1)=7(环)
∵乙的射击成绩从小到大排列为:3,4,6,7,7,8,8,8,9,10
∴乙射击成绩的中位数b=7+8=7.5(环),
乙的方差c=[(3-7)2+(4-7)2+(6-7)2+2(7-7)2+3×(8-7)2+(9-7)2+(10-7)2]=(16+9+1+3+4+9)
=4.2
(2)从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定.
综合以上各因素,若选派一名学生参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
