2018-2019学年度九年级数学上册第一章反比例函数检测题(含答案)
文档属性
| 名称 | 2018-2019学年度九年级数学上册第一章反比例函数检测题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 233.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-08 00:00:00 | ||
图片预览




文档简介
第一章 反比例函数
考试总分: 120 分 考试时间: 100 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
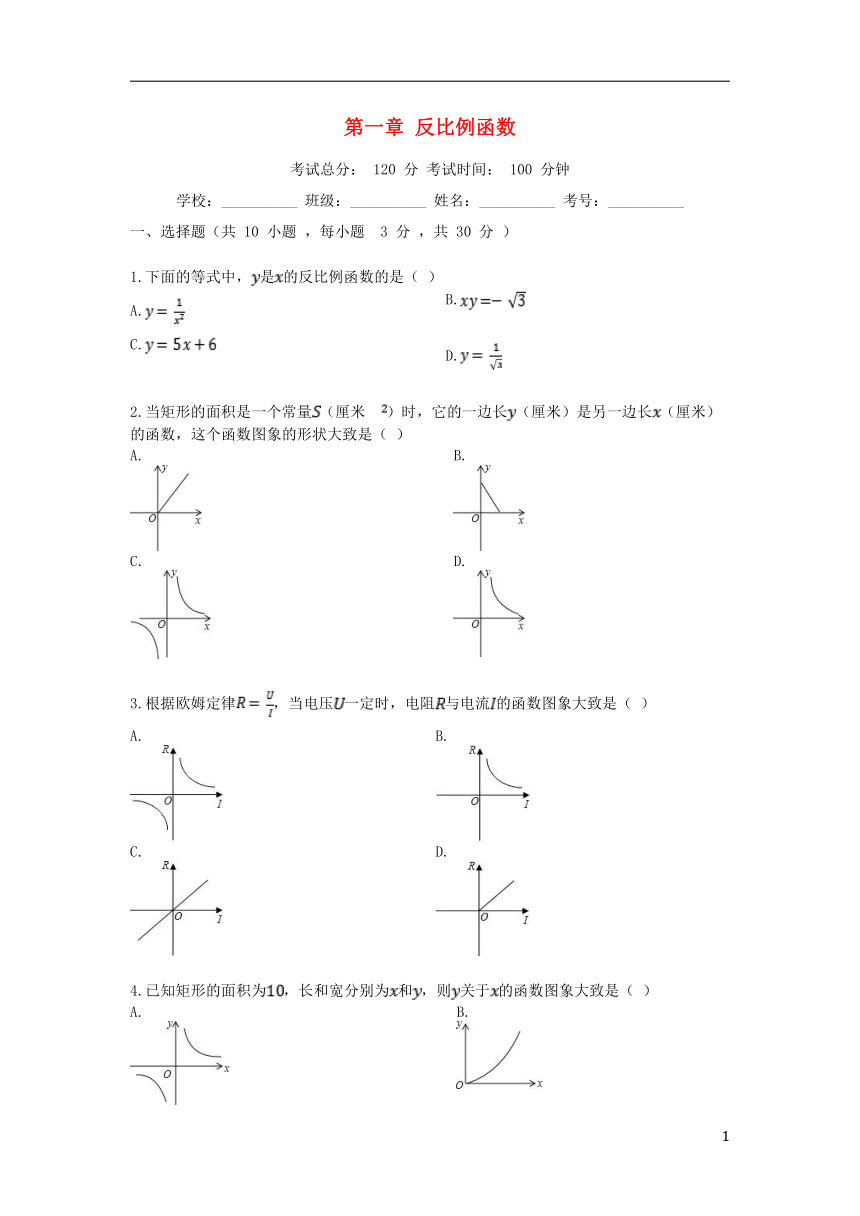
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?
1.下面的等式中,是的反比例函数的是( )
A.
B.
C.
D.
?
2.当矩形的面积是一个常量(厘米)时,它的一边长(厘米)是另一边长(厘米)的函数,这个函数图象的形状大致是( )
A.
B.
C.
D.
?
3.根据欧姆定律,当电压一定时,电阻与电流的函数图象大致是( )
A.
B.
C.
D.
?
4.已知矩形的面积为,长和宽分别为和,则关于的函数图象大致是( )
A.
B.
C.
D.
?
5.如图是三个反比例函数的图象的分支,其中,,的大小关系是( )
A.
B.
C.
D.
?
6.正比例函数与反比例函数的图象有一个交点为,则另一个交点坐标为( )
A.
B.
C.
D.
?
7.边长为的正方形的对称中心是坐标原点,轴,轴,反比例函数与的图象均与正方形的边相交,则图中的阴影部分的面积是( )
A.
B.
C.
D.
?
8.如图所示,点是反比例函数与的一个交点,图中阴影部分的面积为,则反比例函数的解析式为( )
A.
B.
C.
D.
?
9.已知正比例函数与反比例函数的图象交于、两点,若点,则点的坐标为( )
A.
B.
C.
D.
?
10.已知反比例函数,若、、是这个反比例函数图象上的三点,且,,则( )
A.
B.
C.
D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?
11.将反比例函数的图象沿轴向右平移个单位长度后,该图象不经过第________象限.
?
12.已知反比例函数,当________时,其图象的两个分支在第一、三象限内;当________时,其图象在每个象限内随的增大而增大.
?
13.如图,已知点为反比例函数上的一点,过点向坐标轴引垂线,垂足分别为、,那么四边形的面积为________.
?
14.已知反比例函数的图象经过点,则的值是________.
?
15.如图,为双曲线上一点,为轴正半轴上一点,线段的中点恰好在双曲线上,则的积为________.
?
16.在平面直角坐标系中,点是坐标原点,过点的双曲线,且与轴垂直交于点,且,则的值是________.
?
17.如图,直线与双曲线交于、两点,若、两点的坐标分别为, ,则的值为________.
?
18.已知在平面直角坐标系中,有两定点、,是反比例函数图象上动点,当为直角三角形时,点坐标为________.
?
19.设有反比例函数,为其图象上两点,若,,则的取值范围是________.
?
20.如图,点是轴上的一个点,过点作轴的垂线交双曲线于点,的面积是,则双曲线的表达式是________.
三、解答题(共 5 小题 ,每小题 10 分 ,共 50 分 )
?
21.已知反比例函数的图象经过点.
求这个函数的解析式;
判断点,是否在这个函数的图象上,并说明理由.
?
22.如图,一次函数的图象与反比例函数的图象交于、两点,
求反比例函数和一次函数的解析式;
写出使一次函数的值大于反比例函数的的取值范围;
连接、,求的面积.
?
23.在压力不变的情况下,某物体承受的压强是它的受力面积的反比例函数,其图象如图所示.
求与之间的函数关系式;
求当时物体承受的压强.
?
24.如图,为矩形的边上的一个动点,于,,,设,,求与之间的关系式,并写出的取值范围.
?
25.心理学家研究发现,一般情况下,在一节分钟的课中,学生的注意力随老师讲课时间的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指数随时间(分)的变化规律如图所示(其中、分别为线段,为双曲线的一部分);
分别求出线段、和双曲线的函数解析式,并写出自变量的取值范围.
开始上课后第分钟时与第分钟比较,何时学生的注意力更集中?
一道数学竞赛题,需要讲分钟,为了效果较好,要求学生的注意力指数最低达到,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?并说明理由.
答案
1.B
2.D
3.B
4.C
5.C
6.B
7.A
8.D
9.A
10.B
11.二
12.
13.
14.
15.
16.
17.
18.或
19.
20.
21.解:把代入反比例函数中得:, ∴反比例函数解析式为,把代入反比例函数解析式, 把代入反比例函数解析式, 所以不在这个函数的图象上,在这个函数的图象上.
22.解:设一次函数的解析式为,反比例函数的解析式为, 把代入得:, 即反比例函数的解析式为, 把代入得:, 解得:, 即的坐标为, 把、的坐标代入得:, 解得:,, 即一次函数的解析式为;∵函数和的交点为、, ∴使一次函数的值大于反比例函数的的取值范围是或;
设一次函数和轴的交点为,和轴的交点为, 当时,,当时,, 即,, ∵、, ∴的面积为.
23.解:设, ∵点在这个函数的图象上, ∴, ∴, ∴与的函数关系式为;当时,.
24.解:如图,连接. ∵于,四边形是矩形, ∴,, ∴,,, ∴, ∴,, ∴, .
25.解:设线段所在的直线的解析式为, 把代入得,, ∴. 设、所在双曲线的解析式为, 把代入得,, ∴;当时,, 当?, ∴ ∴第分钟注意力更集中.令, ∴, ∴ 令, ∴, ∴ ∵, ∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
考试总分: 120 分 考试时间: 100 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?
1.下面的等式中,是的反比例函数的是( )
A.
B.
C.
D.
?
2.当矩形的面积是一个常量(厘米)时,它的一边长(厘米)是另一边长(厘米)的函数,这个函数图象的形状大致是( )
A.
B.
C.
D.
?
3.根据欧姆定律,当电压一定时,电阻与电流的函数图象大致是( )
A.
B.
C.
D.
?
4.已知矩形的面积为,长和宽分别为和,则关于的函数图象大致是( )
A.
B.
C.
D.
?
5.如图是三个反比例函数的图象的分支,其中,,的大小关系是( )
A.
B.
C.
D.
?
6.正比例函数与反比例函数的图象有一个交点为,则另一个交点坐标为( )
A.
B.
C.
D.
?
7.边长为的正方形的对称中心是坐标原点,轴,轴,反比例函数与的图象均与正方形的边相交,则图中的阴影部分的面积是( )
A.
B.
C.
D.
?
8.如图所示,点是反比例函数与的一个交点,图中阴影部分的面积为,则反比例函数的解析式为( )
A.
B.
C.
D.
?
9.已知正比例函数与反比例函数的图象交于、两点,若点,则点的坐标为( )
A.
B.
C.
D.
?
10.已知反比例函数,若、、是这个反比例函数图象上的三点,且,,则( )
A.
B.
C.
D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?
11.将反比例函数的图象沿轴向右平移个单位长度后,该图象不经过第________象限.
?
12.已知反比例函数,当________时,其图象的两个分支在第一、三象限内;当________时,其图象在每个象限内随的增大而增大.
?
13.如图,已知点为反比例函数上的一点,过点向坐标轴引垂线,垂足分别为、,那么四边形的面积为________.
?
14.已知反比例函数的图象经过点,则的值是________.
?
15.如图,为双曲线上一点,为轴正半轴上一点,线段的中点恰好在双曲线上,则的积为________.
?
16.在平面直角坐标系中,点是坐标原点,过点的双曲线,且与轴垂直交于点,且,则的值是________.
?
17.如图,直线与双曲线交于、两点,若、两点的坐标分别为, ,则的值为________.
?
18.已知在平面直角坐标系中,有两定点、,是反比例函数图象上动点,当为直角三角形时,点坐标为________.
?
19.设有反比例函数,为其图象上两点,若,,则的取值范围是________.
?
20.如图,点是轴上的一个点,过点作轴的垂线交双曲线于点,的面积是,则双曲线的表达式是________.
三、解答题(共 5 小题 ,每小题 10 分 ,共 50 分 )
?
21.已知反比例函数的图象经过点.
求这个函数的解析式;
判断点,是否在这个函数的图象上,并说明理由.
?
22.如图,一次函数的图象与反比例函数的图象交于、两点,
求反比例函数和一次函数的解析式;
写出使一次函数的值大于反比例函数的的取值范围;
连接、,求的面积.
?
23.在压力不变的情况下,某物体承受的压强是它的受力面积的反比例函数,其图象如图所示.
求与之间的函数关系式;
求当时物体承受的压强.
?
24.如图,为矩形的边上的一个动点,于,,,设,,求与之间的关系式,并写出的取值范围.
?
25.心理学家研究发现,一般情况下,在一节分钟的课中,学生的注意力随老师讲课时间的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指数随时间(分)的变化规律如图所示(其中、分别为线段,为双曲线的一部分);
分别求出线段、和双曲线的函数解析式,并写出自变量的取值范围.
开始上课后第分钟时与第分钟比较,何时学生的注意力更集中?
一道数学竞赛题,需要讲分钟,为了效果较好,要求学生的注意力指数最低达到,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?并说明理由.
答案
1.B
2.D
3.B
4.C
5.C
6.B
7.A
8.D
9.A
10.B
11.二
12.
13.
14.
15.
16.
17.
18.或
19.
20.
21.解:把代入反比例函数中得:, ∴反比例函数解析式为,把代入反比例函数解析式, 把代入反比例函数解析式, 所以不在这个函数的图象上,在这个函数的图象上.
22.解:设一次函数的解析式为,反比例函数的解析式为, 把代入得:, 即反比例函数的解析式为, 把代入得:, 解得:, 即的坐标为, 把、的坐标代入得:, 解得:,, 即一次函数的解析式为;∵函数和的交点为、, ∴使一次函数的值大于反比例函数的的取值范围是或;
设一次函数和轴的交点为,和轴的交点为, 当时,,当时,, 即,, ∵、, ∴的面积为.
23.解:设, ∵点在这个函数的图象上, ∴, ∴, ∴与的函数关系式为;当时,.
24.解:如图,连接. ∵于,四边形是矩形, ∴,, ∴,,, ∴, ∴,, ∴, .
25.解:设线段所在的直线的解析式为, 把代入得,, ∴. 设、所在双曲线的解析式为, 把代入得,, ∴;当时,, 当?, ∴ ∴第分钟注意力更集中.令, ∴, ∴ 令, ∴, ∴ ∵, ∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
