(广东专版)2018年秋七年级数学上册第四章基本平面图形单元测试卷(含答案)
文档属性
| 名称 | (广东专版)2018年秋七年级数学上册第四章基本平面图形单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 157.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-09 01:45:29 | ||
图片预览

文档简介
第四章单元测试卷
(时间:100分钟 满分:120分)
一、选择题(本大题10小题,每小题3分,共30分)
1. 下列说法正确的是(B)
A.过一点P只能作一条直线 B.直线AB和直线BA表示同一条直线
C.射线AB和射线BA表示同一条射线 D.射线a比直线b短
2. 下面表示∠ABC的图是(C)
3. 同一平面内互不重合的三条直线的交点的个数是(C)
A.可能是0个,1个,2个 B.可能是0个,2个,3个
C.可能是0个,1个,2个或3个 D.可能是1个或3个
4. 如图,点C,D是线段AB上的两点,且点D是线段AC的中点,若AB=10 cm,BC=4 cm,则AD的长为(B)
A.2 cm B.3 cm C.4 cm D.6 cm
,第4题图) ,第5题图) ,第6题图) ,第9题图)
5. 如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于(C)
A.35° B.70° C.110° D.145°
6. 如图,小红同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是(A)
A.两点之间线段最短 B.两点确定一条直线
C.过一点,有无数条直线 D.连接两点之间的线段叫做两点间的距离
7. 点C是线段AB的中点,点D是BC上一点,则以下关系式中不正确的是(C)
A.CD=AC-BD B.CD=AB-BD C.CD=BC D.CD=AD-BC
8. 下列属于正n边形的特征的有(A)
①各边相等;②各个内角相等;③各条对角线都相等;④从一个顶点可以引(n-2)条对角线;⑤从一个顶点引出的对角线将n边形分成面积相等的(n-2)个三角形.
A.2个 B.3个 C.4个 D.5个
9. 如图,圆的四条半径分别是OA,OB,OC,OD,其中点O,A,B在同一条直线上,∠AOD=90°,∠AOC=3∠BOC,那么圆被四条半径分成的四个扇形的面积的比是(A)
A.1∶2∶2∶3 B.3∶2∶2∶3 C.4∶2∶2∶3 D.1∶2∶2∶1
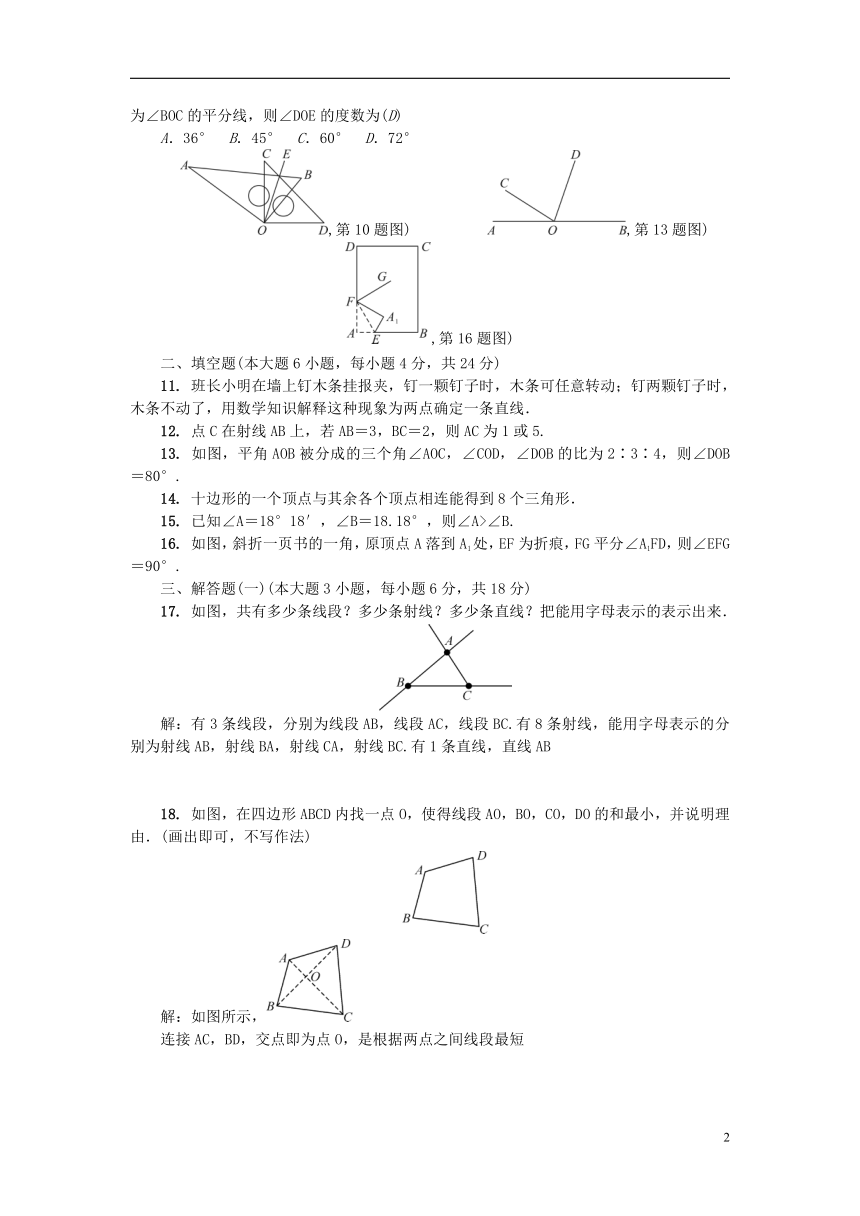
10. 如图,将两块三角尺AOB与COD的直角顶点O重合在一起,若∠AOD=4∠BOC,OE为∠BOC的平分线,则∠DOE的度数为(D)
A.36° B.45° C.60° D.72°
,第10题图) ,第13题图) ,第16题图)
二、填空题(本大题6小题,每小题4分,共24分)
11. 班长小明在墙上钉木条挂报夹,钉一颗钉子时,木条可任意转动;钉两颗钉子时,木条不动了,用数学知识解释这种现象为两点确定一条直线.
12. 点C在射线AB上,若AB=3,BC=2,则AC为1或5.
13. 如图,平角AOB被分成的三个角∠AOC,∠COD,∠DOB的比为2∶3∶4,则∠DOB=80°.
14. 十边形的一个顶点与其余各个顶点相连能得到8个三角形.
15. 已知∠A=18°18′,∠B=18.18°,则∠A>∠B.
16. 如图,斜折一页书的一角,原顶点A落到A1处,EF为折痕,FG平分∠A1FD,则∠EFG=90°.
三、解答题(一)(本大题3小题,每小题6分,共18分)
17. 如图,共有多少条线段?多少条射线?多少条直线?把能用字母表示的表示出来.
解:有3条线段,分别为线段AB,线段AC,线段BC.有8条射线,能用字母表示的分别为射线AB,射线BA,射线CA,射线BC.有1条直线,直线AB
18. 如图,在四边形ABCD内找一点O,使得线段AO,BO,CO,DO的和最小,并说明理由.(画出即可,不写作法)
解:如图所示,
连接AC,BD,交点即为点O,是根据两点之间线段最短
19. 如图,AB=6 cm,延长AB到点C,使BC=3AB,点D是BC的中点,求AD的长度.
解:因为AB=6 cm,BC=3AB,所以BC=18 cm,因为点D为BC的中点,所以BD=9 cm,所以AD=AB+BD=15(cm)
四、解答题(二)(本大题3小题,每小题7分,共21分)
20. 如图,已知线段a,b和射线OA.
(1)在OA上截取OB=2a+b,OC=2a-b;
(2)若a=3,b=2,求BC.
解:(1)如图,OB,OC即为所求
(2)BC=BO-CO=2a+b-(2a-b)=2b=2×2=4
21. 如图,在O点的观测站测得渔船A,B的方向分别为北偏东45°,南偏西30°,为了减少相互干扰并取得较好的捕鱼效益,渔船C恰好位于∠AOB的平分线上,求渔船C相对观测站的方向.
解:由题意可知,∠AOB=180°-45°+30°=165°,165°÷2-30°=52.5°,所以点C在观测点南偏东52.5°方向
22. 如图,OE为∠AOD的平分线,∠COD=∠EOC,∠COD=15°.求:
(1)∠EOC的大小;
(2)∠AOD的大小.
解:(1)由∠COD=∠EOC,得∠EOC=4∠COD=4×15°=60°
(2)因为∠EOD=∠EOC-∠COD=60°-15°=45°.由角平分线的性质,得∠AOD=2∠EOD=2×45°=90°
五、解答题(三)(本大题3小题,每小题9分,共27分)
23. 如图,点C在线段AB上,AC=8 cm,BC=6 cm,点M,N分别是AC,BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任意一点,满足AB=AC+BC=a cm,其他条件不变,试求线段MN的长;
(3)若C在线段AB的延长线上,且满足AB=AC-BC=b cm,点M,N分别是AC,BC的中点,试求线段MN的长,并画出图形.
解:(1)MN=MC+CN=AC+BC=4+3=7(cm)
(2)MN=MC+CN=AC+BC=(AC+BC)=(cm)
(3)如图所示:
MN=MC-NC=AC-BC=(AC-BC)=(cm)
24.钟面角是指时钟的时针与分针所成的角.如图,在钟面上,点O为钟面的圆心,图中的圆我们称之为钟面圆.为便于研究,我们规定:钟面圆的半径OA表示时针,半径OB表示分针,它们所成的钟面角为∠AOB;本题中所提到的角都不小于0°,且不大于180°.本题中所指的时刻都介于0点整到12点整之间.
(1)时针每分钟转动的角度为0.5°,分针每分钟转动的角度为6°;
(2)8点整,钟面角∠AOB=120°,钟面角与此相等的整点还有:4点整;
(3)如图,设半径OC指向12点方向,在图中画出6点15分时半径OA,OB的大概位置,并求出此时∠AOB的度数.
解:(3)如图:
∠AOB=6×30+15×0.5-15×6=97.5°
25. 乐乐对几何中角平分线等兴趣浓厚,请你和乐乐一起探究下面问题吧.已知∠AOB=100°,射线OE,OF分别是∠AOC和∠COB的角平分线.
(1)如图①,若射线OC在∠AOB的内部,且∠AOC=30°,求∠EOF得度数;
(2)如图②,若射线OC在∠AOB的内部绕点O旋转,求∠EOF的度数;
(3)若射线OC在∠AOB的外部绕点O旋转(旋转中∠AOC,∠BOC均指小于180°的角),其余条件不变,请借助图③探究∠EOF的大小,写出∠EOF的度数.
解:(1)因为∠AOB=100°,∠AOC=30°,所以∠BOC=∠AOB-∠AOC=70°,因为OE,OF分别是∠AOC和∠COB的角平分线,所以∠EOC=∠AOC=15°,∠FOC=∠BOC=35°,所以∠EOF=∠EOC+∠FOC=15°+35°=50°
(2)因为OE,OF分别是∠AOC和∠COB的角平分线,所以∠EOC=∠AOC,∠FOC=∠BOC,所以∠EOF=∠EOC+∠FOC=∠AOB=×100°=50°
(3)①射线OE,OF只有1条射线在∠AOB外面,如图④,∠EOF=∠FOC-∠COE=∠BOC-∠AOC=∠AOB=×100°=50°;②射线OE,OF都在∠AOB外面,如图⑤,∠EOF=∠EOC+∠COF=∠AOC+∠BOC=(∠AOC+∠BOC)=(360°-∠AOB)=×260°=130°.故∠EOF的度数是50°或130°
(时间:100分钟 满分:120分)
一、选择题(本大题10小题,每小题3分,共30分)
1. 下列说法正确的是(B)
A.过一点P只能作一条直线 B.直线AB和直线BA表示同一条直线
C.射线AB和射线BA表示同一条射线 D.射线a比直线b短
2. 下面表示∠ABC的图是(C)
3. 同一平面内互不重合的三条直线的交点的个数是(C)
A.可能是0个,1个,2个 B.可能是0个,2个,3个
C.可能是0个,1个,2个或3个 D.可能是1个或3个
4. 如图,点C,D是线段AB上的两点,且点D是线段AC的中点,若AB=10 cm,BC=4 cm,则AD的长为(B)
A.2 cm B.3 cm C.4 cm D.6 cm
,第4题图) ,第5题图) ,第6题图) ,第9题图)
5. 如图,点O在直线AB上,射线OC平分∠DOB.若∠COB=35°,则∠AOD等于(C)
A.35° B.70° C.110° D.145°
6. 如图,小红同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是(A)
A.两点之间线段最短 B.两点确定一条直线
C.过一点,有无数条直线 D.连接两点之间的线段叫做两点间的距离
7. 点C是线段AB的中点,点D是BC上一点,则以下关系式中不正确的是(C)
A.CD=AC-BD B.CD=AB-BD C.CD=BC D.CD=AD-BC
8. 下列属于正n边形的特征的有(A)
①各边相等;②各个内角相等;③各条对角线都相等;④从一个顶点可以引(n-2)条对角线;⑤从一个顶点引出的对角线将n边形分成面积相等的(n-2)个三角形.
A.2个 B.3个 C.4个 D.5个
9. 如图,圆的四条半径分别是OA,OB,OC,OD,其中点O,A,B在同一条直线上,∠AOD=90°,∠AOC=3∠BOC,那么圆被四条半径分成的四个扇形的面积的比是(A)
A.1∶2∶2∶3 B.3∶2∶2∶3 C.4∶2∶2∶3 D.1∶2∶2∶1
10. 如图,将两块三角尺AOB与COD的直角顶点O重合在一起,若∠AOD=4∠BOC,OE为∠BOC的平分线,则∠DOE的度数为(D)
A.36° B.45° C.60° D.72°
,第10题图) ,第13题图) ,第16题图)
二、填空题(本大题6小题,每小题4分,共24分)
11. 班长小明在墙上钉木条挂报夹,钉一颗钉子时,木条可任意转动;钉两颗钉子时,木条不动了,用数学知识解释这种现象为两点确定一条直线.
12. 点C在射线AB上,若AB=3,BC=2,则AC为1或5.
13. 如图,平角AOB被分成的三个角∠AOC,∠COD,∠DOB的比为2∶3∶4,则∠DOB=80°.
14. 十边形的一个顶点与其余各个顶点相连能得到8个三角形.
15. 已知∠A=18°18′,∠B=18.18°,则∠A>∠B.
16. 如图,斜折一页书的一角,原顶点A落到A1处,EF为折痕,FG平分∠A1FD,则∠EFG=90°.
三、解答题(一)(本大题3小题,每小题6分,共18分)
17. 如图,共有多少条线段?多少条射线?多少条直线?把能用字母表示的表示出来.
解:有3条线段,分别为线段AB,线段AC,线段BC.有8条射线,能用字母表示的分别为射线AB,射线BA,射线CA,射线BC.有1条直线,直线AB
18. 如图,在四边形ABCD内找一点O,使得线段AO,BO,CO,DO的和最小,并说明理由.(画出即可,不写作法)
解:如图所示,
连接AC,BD,交点即为点O,是根据两点之间线段最短
19. 如图,AB=6 cm,延长AB到点C,使BC=3AB,点D是BC的中点,求AD的长度.
解:因为AB=6 cm,BC=3AB,所以BC=18 cm,因为点D为BC的中点,所以BD=9 cm,所以AD=AB+BD=15(cm)
四、解答题(二)(本大题3小题,每小题7分,共21分)
20. 如图,已知线段a,b和射线OA.
(1)在OA上截取OB=2a+b,OC=2a-b;
(2)若a=3,b=2,求BC.
解:(1)如图,OB,OC即为所求
(2)BC=BO-CO=2a+b-(2a-b)=2b=2×2=4
21. 如图,在O点的观测站测得渔船A,B的方向分别为北偏东45°,南偏西30°,为了减少相互干扰并取得较好的捕鱼效益,渔船C恰好位于∠AOB的平分线上,求渔船C相对观测站的方向.
解:由题意可知,∠AOB=180°-45°+30°=165°,165°÷2-30°=52.5°,所以点C在观测点南偏东52.5°方向
22. 如图,OE为∠AOD的平分线,∠COD=∠EOC,∠COD=15°.求:
(1)∠EOC的大小;
(2)∠AOD的大小.
解:(1)由∠COD=∠EOC,得∠EOC=4∠COD=4×15°=60°
(2)因为∠EOD=∠EOC-∠COD=60°-15°=45°.由角平分线的性质,得∠AOD=2∠EOD=2×45°=90°
五、解答题(三)(本大题3小题,每小题9分,共27分)
23. 如图,点C在线段AB上,AC=8 cm,BC=6 cm,点M,N分别是AC,BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任意一点,满足AB=AC+BC=a cm,其他条件不变,试求线段MN的长;
(3)若C在线段AB的延长线上,且满足AB=AC-BC=b cm,点M,N分别是AC,BC的中点,试求线段MN的长,并画出图形.
解:(1)MN=MC+CN=AC+BC=4+3=7(cm)
(2)MN=MC+CN=AC+BC=(AC+BC)=(cm)
(3)如图所示:
MN=MC-NC=AC-BC=(AC-BC)=(cm)
24.钟面角是指时钟的时针与分针所成的角.如图,在钟面上,点O为钟面的圆心,图中的圆我们称之为钟面圆.为便于研究,我们规定:钟面圆的半径OA表示时针,半径OB表示分针,它们所成的钟面角为∠AOB;本题中所提到的角都不小于0°,且不大于180°.本题中所指的时刻都介于0点整到12点整之间.
(1)时针每分钟转动的角度为0.5°,分针每分钟转动的角度为6°;
(2)8点整,钟面角∠AOB=120°,钟面角与此相等的整点还有:4点整;
(3)如图,设半径OC指向12点方向,在图中画出6点15分时半径OA,OB的大概位置,并求出此时∠AOB的度数.
解:(3)如图:
∠AOB=6×30+15×0.5-15×6=97.5°
25. 乐乐对几何中角平分线等兴趣浓厚,请你和乐乐一起探究下面问题吧.已知∠AOB=100°,射线OE,OF分别是∠AOC和∠COB的角平分线.
(1)如图①,若射线OC在∠AOB的内部,且∠AOC=30°,求∠EOF得度数;
(2)如图②,若射线OC在∠AOB的内部绕点O旋转,求∠EOF的度数;
(3)若射线OC在∠AOB的外部绕点O旋转(旋转中∠AOC,∠BOC均指小于180°的角),其余条件不变,请借助图③探究∠EOF的大小,写出∠EOF的度数.
解:(1)因为∠AOB=100°,∠AOC=30°,所以∠BOC=∠AOB-∠AOC=70°,因为OE,OF分别是∠AOC和∠COB的角平分线,所以∠EOC=∠AOC=15°,∠FOC=∠BOC=35°,所以∠EOF=∠EOC+∠FOC=15°+35°=50°
(2)因为OE,OF分别是∠AOC和∠COB的角平分线,所以∠EOC=∠AOC,∠FOC=∠BOC,所以∠EOF=∠EOC+∠FOC=∠AOB=×100°=50°
(3)①射线OE,OF只有1条射线在∠AOB外面,如图④,∠EOF=∠FOC-∠COE=∠BOC-∠AOC=∠AOB=×100°=50°;②射线OE,OF都在∠AOB外面,如图⑤,∠EOF=∠EOC+∠COF=∠AOC+∠BOC=(∠AOC+∠BOC)=(360°-∠AOB)=×260°=130°.故∠EOF的度数是50°或130°
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
