第二章匀变速直线运动的研究2.3匀变速直线运动的位移与时间的关系课件:21张PPT
文档属性
| 名称 | 第二章匀变速直线运动的研究2.3匀变速直线运动的位移与时间的关系课件:21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 545.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2018-10-09 00:00:00 | ||
图片预览






文档简介
课件21张PPT。3 匀变速直线运动的位移与时间的关系1.认识什么是匀变速直线运动,并知道匀变速直线运动的分类。
2.理解匀变速直线运动的x-t图象特点。
3.理解匀变速直线运动的位移与时间的关系。
4.会用速度公式解决简单的匀变速直线运动问题。一二一、匀速直线运动的位移
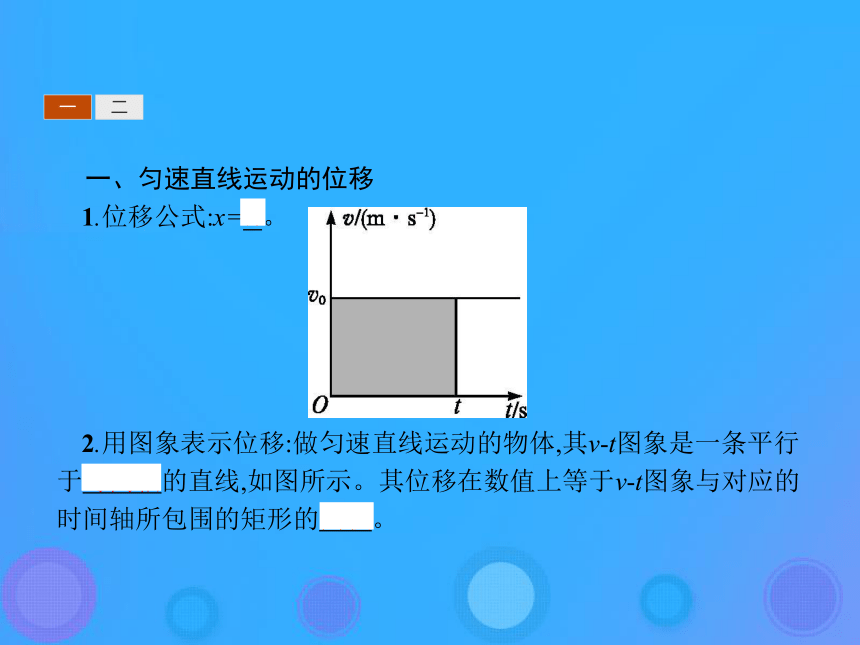
1.位移公式:x=vt。
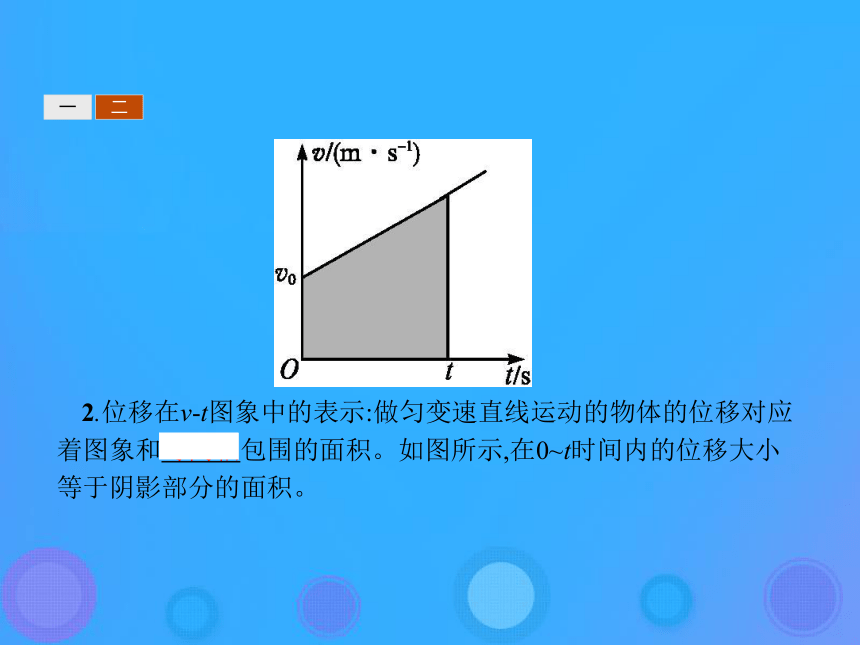
2.用图象表示位移:做匀速直线运动的物体,其v-t图象是一条平行于时间轴的直线,如图所示。其位移在数值上等于v-t图象与对应的时间轴所包围的矩形的面积。一二一二2.位移在v-t图象中的表示:做匀变速直线运动的物体的位移对应着图象和时间轴包围的面积。如图所示,在0~t时间内的位移大小等于阴影部分的面积。一二一二三一、利用速度图象求匀变速直线运动的位移
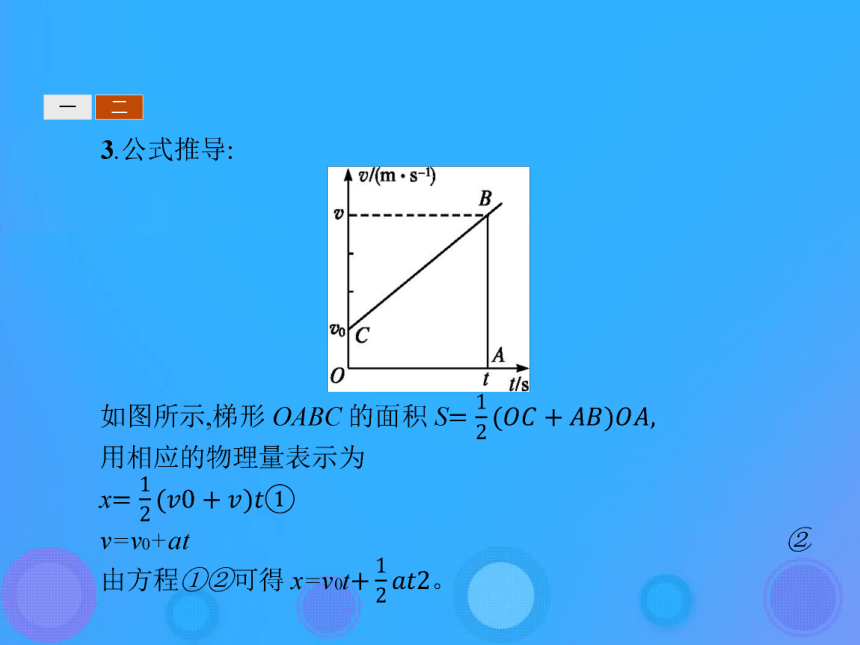
如图所示,图中的倾斜直线AB表示一个做匀变速直线运动物体的v-t图象。为了求出物体在时间t内的位移,我们把时间划分为许多小的时间间隔。设想物体在每一时间间隔内都做匀速直线运动,而从一个时间间隔到下一个时间间隔,物体的速度发生跳跃性的变化。因此,它的v-t图象由图中的一些平行于时间轴的间断线段组成。由于匀速直线运动的位移可以用v-t图象与时间轴之间的面积来表示,因此上面设想的物体在时间t内运动的位移,可用图中的一个个小矩形面积之和(即阶梯状折线与时间轴之间的面积)来表示。一二三如果时间的分割再细些,物体速度的跃变发生得更频繁,它的v-t图象就更接近于物体的真实运动的图象,阶梯状折线与时间轴之间的面积就更接近于倾斜直线AB与时间轴之间的面积。当时间间隔无限细分时,间断的阶梯线段就趋向于倾斜直线AB,阶梯状折线与时间轴之间的面积就趋向于倾斜直线AB与时间轴之间的面积。这样,我们就得出结论:匀变速直线运动的位移也可以用v-t图象与时间轴之间的面积来表示。
运用类似的分析方法可以得出,上述结论不仅对匀变速直线运动适用,对一般的变速直线运动也是适用的。一二三一二三一二三三、匀变速直线运动的两个重要推论
1.平均速度
做匀变速直线运动的物体,在一段时间内的平均速度等于这段时间内中间时刻的瞬时速度,还等于这段时间初、末速度矢量和的一半。
推导:设物体的初速度为v0,做匀变速直线运动的加速度为a,t时刻的速度为v。一二三一二三类型一类型二类型三【例题1】 一辆卡车初速度为v0=10 m/s,以a=2 m/s2的加速度行驶,求:
(1)卡车在3 s末的速度v3;
(2)卡车在6 s内的位移x6与平均速度v;
(3)卡车在第6 s内的位移x。
点拨:卡车做匀加速直线运动,根据速度公式可求得 3 s末的速度,根据位移公式可求得6 s内的位移。第6 s内的位移等于前6 s内的位移减去前5 s内的位移。类型一类型二类型三答案:(1)16 m/s (2)96 m 16 m/s (3)21 m题后反思正确应用匀变速直线运动的速度公式和位移公式是解决本题的关键。 类型一类型二类型三【例题2】
(多选)某物体运动的v-t图象如图所示,下列说法正确的是( )
A.物体在第1 s末运动方向发生变化
B.物体在第2 s内和第3 s内的加速度是相同的
C.物体在4 s末返回出发点
D.物体在6 s末离出发点最远,且最大位移为1 m
点拨:用v-t图象分析问题时要注意:(1)v-t图象中直线的斜率表示物体运动的加速度;(2)图线和t轴所围的面积的数值等于物体的位移大小,图线和t轴所围成的面积的数值的绝对值的和等于物体的路程。类型一类型二类型三解析:由题图可知,物体在前2 s内速度先增大后减小,但运动方向没有变化,选项A错误;第2 s内和第3 s内图线的斜率没变,所以加速度相同,选项B正确;在v-t图象中,图线与坐标轴所围的“面积”表示物体的位移,从图象可以看出,前4 s内物体的位移为零,所以物体在4 s末返回出发点,选项C正确;物体在第6 s末离出发点最远,6 s内的位移为1 m,选项D正确。
答案:BCD类型一类型二类型三【例题3】 一辆小汽车在一段平直的高速公路上匀速行驶,速度大小为v0=108 km/h,由于前方出现险情,司机紧急刹车,刹车时汽车的加速度大小为5 m/s2。求:
(1)汽车开始制动后t1=10 s内滑行的距离;
(2)开始制动后汽车发生位移x=80 m所经历的时间t2。类型一类型二类型三答案:(1)90 m (2)4 s 类型一类型二类型三类型一类型二类型三触类旁通试求汽车刹车后最后2 s的初速度和最后2 s内的位移。
解析:汽车在最后2 s的初速度和最后2 s内的位移可逆向按初速度为零的匀加速直线运动处理。
最后2 s的初速度
v=at=5×2 m/s=10 m/s
最后2 s内的位移
答案:10 m/s 10 m
2.理解匀变速直线运动的x-t图象特点。
3.理解匀变速直线运动的位移与时间的关系。
4.会用速度公式解决简单的匀变速直线运动问题。一二一、匀速直线运动的位移
1.位移公式:x=vt。
2.用图象表示位移:做匀速直线运动的物体,其v-t图象是一条平行于时间轴的直线,如图所示。其位移在数值上等于v-t图象与对应的时间轴所包围的矩形的面积。一二一二2.位移在v-t图象中的表示:做匀变速直线运动的物体的位移对应着图象和时间轴包围的面积。如图所示,在0~t时间内的位移大小等于阴影部分的面积。一二一二三一、利用速度图象求匀变速直线运动的位移
如图所示,图中的倾斜直线AB表示一个做匀变速直线运动物体的v-t图象。为了求出物体在时间t内的位移,我们把时间划分为许多小的时间间隔。设想物体在每一时间间隔内都做匀速直线运动,而从一个时间间隔到下一个时间间隔,物体的速度发生跳跃性的变化。因此,它的v-t图象由图中的一些平行于时间轴的间断线段组成。由于匀速直线运动的位移可以用v-t图象与时间轴之间的面积来表示,因此上面设想的物体在时间t内运动的位移,可用图中的一个个小矩形面积之和(即阶梯状折线与时间轴之间的面积)来表示。一二三如果时间的分割再细些,物体速度的跃变发生得更频繁,它的v-t图象就更接近于物体的真实运动的图象,阶梯状折线与时间轴之间的面积就更接近于倾斜直线AB与时间轴之间的面积。当时间间隔无限细分时,间断的阶梯线段就趋向于倾斜直线AB,阶梯状折线与时间轴之间的面积就趋向于倾斜直线AB与时间轴之间的面积。这样,我们就得出结论:匀变速直线运动的位移也可以用v-t图象与时间轴之间的面积来表示。
运用类似的分析方法可以得出,上述结论不仅对匀变速直线运动适用,对一般的变速直线运动也是适用的。一二三一二三一二三三、匀变速直线运动的两个重要推论
1.平均速度
做匀变速直线运动的物体,在一段时间内的平均速度等于这段时间内中间时刻的瞬时速度,还等于这段时间初、末速度矢量和的一半。
推导:设物体的初速度为v0,做匀变速直线运动的加速度为a,t时刻的速度为v。一二三一二三类型一类型二类型三【例题1】 一辆卡车初速度为v0=10 m/s,以a=2 m/s2的加速度行驶,求:
(1)卡车在3 s末的速度v3;
(2)卡车在6 s内的位移x6与平均速度v;
(3)卡车在第6 s内的位移x。
点拨:卡车做匀加速直线运动,根据速度公式可求得 3 s末的速度,根据位移公式可求得6 s内的位移。第6 s内的位移等于前6 s内的位移减去前5 s内的位移。类型一类型二类型三答案:(1)16 m/s (2)96 m 16 m/s (3)21 m题后反思正确应用匀变速直线运动的速度公式和位移公式是解决本题的关键。 类型一类型二类型三【例题2】
(多选)某物体运动的v-t图象如图所示,下列说法正确的是( )
A.物体在第1 s末运动方向发生变化
B.物体在第2 s内和第3 s内的加速度是相同的
C.物体在4 s末返回出发点
D.物体在6 s末离出发点最远,且最大位移为1 m
点拨:用v-t图象分析问题时要注意:(1)v-t图象中直线的斜率表示物体运动的加速度;(2)图线和t轴所围的面积的数值等于物体的位移大小,图线和t轴所围成的面积的数值的绝对值的和等于物体的路程。类型一类型二类型三解析:由题图可知,物体在前2 s内速度先增大后减小,但运动方向没有变化,选项A错误;第2 s内和第3 s内图线的斜率没变,所以加速度相同,选项B正确;在v-t图象中,图线与坐标轴所围的“面积”表示物体的位移,从图象可以看出,前4 s内物体的位移为零,所以物体在4 s末返回出发点,选项C正确;物体在第6 s末离出发点最远,6 s内的位移为1 m,选项D正确。
答案:BCD类型一类型二类型三【例题3】 一辆小汽车在一段平直的高速公路上匀速行驶,速度大小为v0=108 km/h,由于前方出现险情,司机紧急刹车,刹车时汽车的加速度大小为5 m/s2。求:
(1)汽车开始制动后t1=10 s内滑行的距离;
(2)开始制动后汽车发生位移x=80 m所经历的时间t2。类型一类型二类型三答案:(1)90 m (2)4 s 类型一类型二类型三类型一类型二类型三触类旁通试求汽车刹车后最后2 s的初速度和最后2 s内的位移。
解析:汽车在最后2 s的初速度和最后2 s内的位移可逆向按初速度为零的匀加速直线运动处理。
最后2 s的初速度
v=at=5×2 m/s=10 m/s
最后2 s内的位移
答案:10 m/s 10 m
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
