1.2矩形的性质与判定课件(共31张PPT)
文档属性
| 名称 | 1.2矩形的性质与判定课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 272.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-10-09 12:36:48 | ||
图片预览







文档简介
课件31张PPT。矩形的性质与判定21、能用综合法证明矩形的性质定理、判定定理以及相关结论;
2、能用矩形的性质进行简单的证明与计算.请从边、角、对角线三个方面说一说平行四边形有哪些性质?边:对边平行且相等;
角:对角相等;
对角线:对角线互相平分. 一位很有名望的木工师傅,招收了两名徒弟,一天,师傅有事外出,两徒弟就自已在家练习用两块四边形的废料各做了一扇矩形式的门,完事之后,两人都说对方的门不是矩形,而自已的是矩形。
甲的理由是:“我用角尺量我的门任意三个角,发现它们都是直角。所以我这个四边形门就是矩形”。
乙的理由是:“我用直尺量这个门的两条对角线,发现它们的长度相等,所以我这个四边形门就是矩形”。
根据它们的对话,你能肯定谁的门一定是矩形。
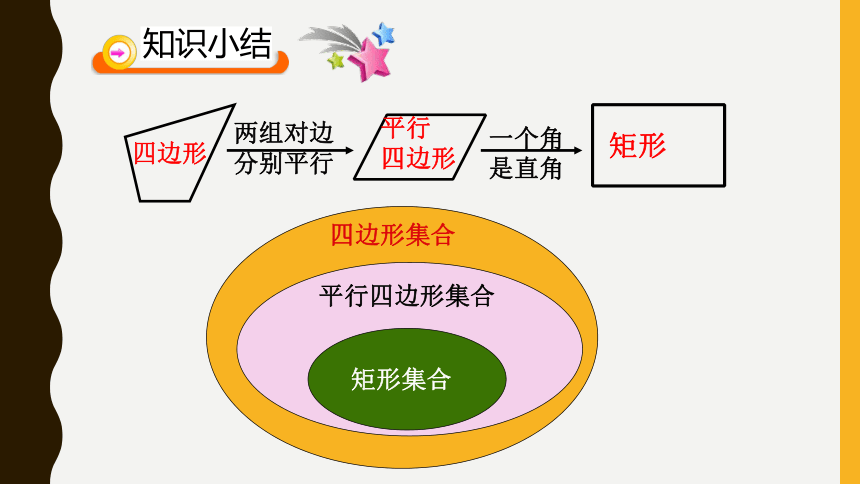
4思考:如何判定一个平行四边形是矩形?矩形的定义:有一个角是直角的平行四边形是矩形。深入思考:你还有其它的判定方法吗?∠A=900四边形ABCD是矩形5小结:
(1)矩形的形成过程是平行四边形的一个角由量变到质变的变化过程.
(2)矩形只比平行四边形多一个条件:“一个角是直角”,不能用“四个角都是直角的平行四边形是矩形”来定义矩形.
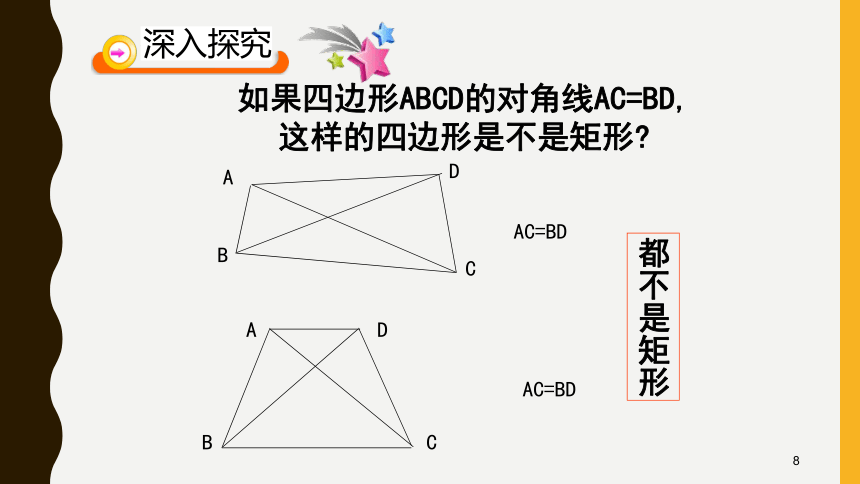
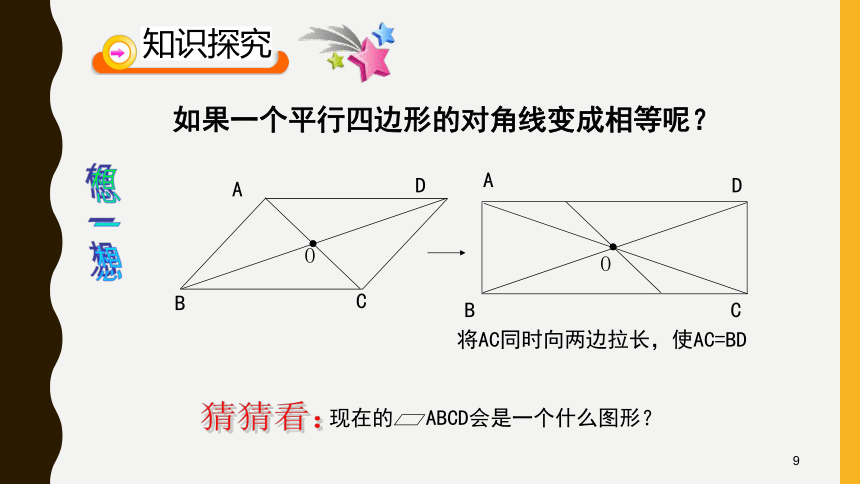
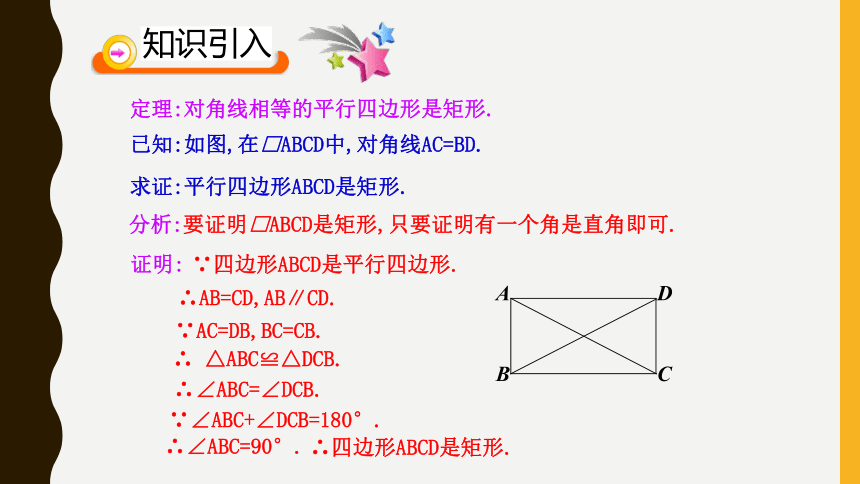
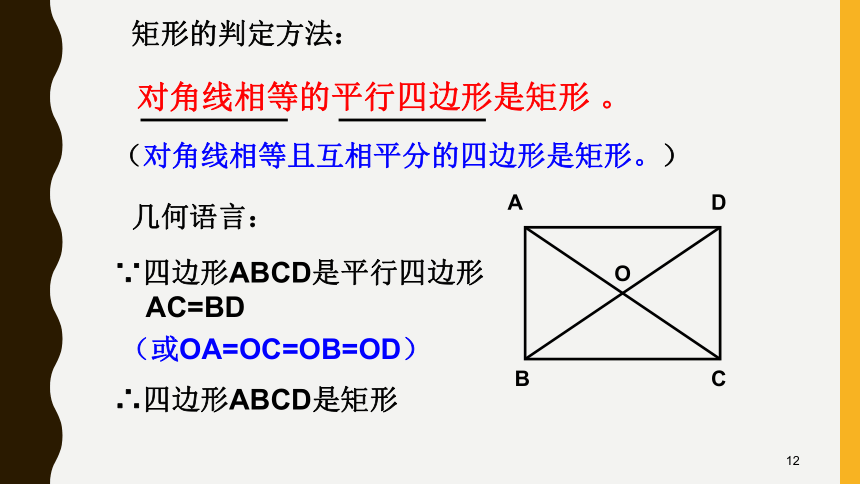
定义:有一个角是直角的平行四边形是矩形.四边形如果四边形ABCD的对角线AC=BD,这样的四边形是不是矩形?AC=BDAC=BD都不是矩形8O如果一个平行四边形的对角线变成相等呢?将AC同时向两边拉长,使AC=BD想一想猜猜看:9情境一:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?猜想:对角线相等的平行四边形是矩形 。10定理:对角线相等的平行四边形是矩形.已知:如图,在□ABCD中,对角线AC=BD.求证:平行四边形ABCD是矩形.分析:要证明□ABCD是矩形,只要证明有一个角是直角即可.证明:∴AB=CD,AB∥CD.∵AC=DB,BC=CB.∴ △ABC≌△DCB.∴∠ABC=∠DCB.∵四边形ABCD是平行四边形.∵∠ABC+∠DCB=180°.∴∠ABC=90°.∴四边形ABCD是矩形.对角线相等的平行四边形是矩形 。矩形的判定方法:几何语言:∵四边形ABCD是平行四边形
AC=BD∴四边形ABCD是矩形(对角线相等且互相平分的四边形是矩形。)(或OA=OC=OB=OD)12四边形有一个角是直角
有两个角是直角 的 四边形是矩形吗?
有三个角是直角
探究14情境一:李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?猜想:有三个角是直角的四边形是矩形 。你能证明上述结论吗?15定理:有三个角是直角的四边形是矩形.已知:如图,在四边形ABCD中, ∠A=∠B=∠C=90°.分析:利用同旁内角互补,两直线平行来证明四边形是平行四边形,可使问题得证.证明:∵ ∠A=∠B=∠C=90°.∴∠A+∠B=180°,∠B+∠C=180°.∴AD∥BC,AB∥CD.求证:四边形ABCD是矩形.∴四边形ABCD是平行四边形.∴四边形ABCD是矩形.矩形的判定方法:有三个角是直角的四边形是矩形 。 ∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形几何语言:17四边形有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形 。(对角线相等且互相平分的四边形是矩形。)有三个角是直角的四边形是矩形 。方法1:方法2:方法3:19矩形的三种判定方法定理:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.证明:∵ 四边形ABCD是矩形.∴∠A=90?,四边形ABCD是平行四边形.∴∠C=∠A=90?,
∠B=180?-∠A=90?,
∠D=180?-∠A=90?.求证:∠A=∠B=∠C=∠D=90?.∴四边形ABCD是矩形.定理:矩形的两条对角线相等.已知:如图,AC,BD是矩形ABCD的两条对角线.求证: AC=BD.证明:∵ 四边形ABCD是矩形.∴AB=DC,∠ABC=∠DCB=90°.分析:根据矩形的性质,可转化
为全等三角形(SAS)来证明.∵BC=CB.∴△ABC≌△DCB(SAS).∴AC=DB.定理:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.求证:△ABC是直角三角形.已知:CD是△ABC边AB上的中线,且分析:要证明△ABC是直角三角形,可以将点A,B,C构造平行四边形,然后证明其对角线相等,即可证明是矩形.下列各句判定矩形的说法是否正确?为什么?
(1)对角线相等的四边形是矩形;( )
(2)对角线互相平分且相等的四边形是矩形;( )
(3)有四个角是直角的四边形是矩形;( )
(4)对角线相等,且有一个角是直角的四边形是矩形;( )XX√ √ 谈一谈,今天你有何收获?1.判定一个四边形是矩形的方法是:本节课我们学习了什么内容,你能总结吗?小结:矩形的判定方法有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形 。(对角线相等且互相平分的四边形是矩形。)有三个角是直角的四边形是矩形 。方法1:方法2:方法3:25通过本课时的学习,需要我们掌握:
1、矩形的性质:
(1)矩形的四个角都是直角;
(2)矩形的对角线相等;
(3)推论:直角三角形斜边上的中线等于斜边的一半.
2、矩形的判定定理:
(1)定义:有一个角是直角的平行四边形是矩形;
(2)对角线相等的平行四边形是矩形;
(3)有三个角是直角的四边形是矩形.
3、直角三角形斜边上的中线等于斜边上的一半.1.如图所示,已知□ABCD,下列条件:①AC=BD,②AB=AD,③∠1=∠2,④AB⊥BC中,能说明□ABCD是矩形的有 (填写序号).解析:根据对角线相等的平行四边形是矩形;矩形的定义.
答案:① ④2.如图,在△ABC中,AB=AC=8,AD是底边上的高,E为AC的中点,则DE= .解析:根据直角三角形斜边的中线等于斜边的一半可得,DE等于AC的一半,所以DE=4.
答案:43.如图,在等边△ABC中,点D是BC边的中点,以AD为边作等边△ADE.(1)求∠CAE的度数;
(2)取AB边的中点F,连结CF、CE,试证明四边形AFCE是矩形.解析:(1)在等边△ABC中,∵点D是BC边的中点,∴∠DAC=30o,又∵等边△ADE,∴∠DAE=60o,∴∠CAE=30o.(2)在等边△ABC中,∵F是AB边的中点,D是BC边的中点,∴CF=AD,∠CFA=90o,又∵AD=AE,∴AE=CF,由(1)知∠CAE=30o,∴∠EAF=60o+30o=90o,∴∠CFA=∠EAF,∴CF∥AE,∵AE=CF,∴四边形AFCE是平行四边形,又∵∠CFA=90o,∴四边形AFCE是矩形.4.已知:如图,四边形ABCD是由两个全等的正三角形ABD和BCD组成的,M、N分别为BC、AD的中点.
求证:四边形BMDN是矩形.证明:在正三角形ABD和BCD中,M、N分别为BC、AD的中点.
∴BN⊥AD,DM⊥BC,∠DBC=60°,
∠BND=∠DMB=90°,∠NBD=30°.
∴∠NBM=90°.
∴四边形BMDN是矩形.5、已知:如图,AC,BD是矩形ABCD的两条对角线,AC,BD相交于点O,∠AOD=120°,AB=2.5cm.求矩形对角线的长.
解:∵四边形ABCD是矩形.
∴AC=BD,且
∴OA=OD.
∵∠AOD=120°.
∴∠ODA=∠OAD=
∵∠DAB=90°.
∴BD=2AB=2×2.5=5(cm).你认为本题还可以怎样解?
2、能用矩形的性质进行简单的证明与计算.请从边、角、对角线三个方面说一说平行四边形有哪些性质?边:对边平行且相等;
角:对角相等;
对角线:对角线互相平分. 一位很有名望的木工师傅,招收了两名徒弟,一天,师傅有事外出,两徒弟就自已在家练习用两块四边形的废料各做了一扇矩形式的门,完事之后,两人都说对方的门不是矩形,而自已的是矩形。
甲的理由是:“我用角尺量我的门任意三个角,发现它们都是直角。所以我这个四边形门就是矩形”。
乙的理由是:“我用直尺量这个门的两条对角线,发现它们的长度相等,所以我这个四边形门就是矩形”。
根据它们的对话,你能肯定谁的门一定是矩形。
4思考:如何判定一个平行四边形是矩形?矩形的定义:有一个角是直角的平行四边形是矩形。深入思考:你还有其它的判定方法吗?∠A=900四边形ABCD是矩形5小结:
(1)矩形的形成过程是平行四边形的一个角由量变到质变的变化过程.
(2)矩形只比平行四边形多一个条件:“一个角是直角”,不能用“四个角都是直角的平行四边形是矩形”来定义矩形.
定义:有一个角是直角的平行四边形是矩形.四边形如果四边形ABCD的对角线AC=BD,这样的四边形是不是矩形?AC=BDAC=BD都不是矩形8O如果一个平行四边形的对角线变成相等呢?将AC同时向两边拉长,使AC=BD想一想猜猜看:9情境一:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?猜想:对角线相等的平行四边形是矩形 。10定理:对角线相等的平行四边形是矩形.已知:如图,在□ABCD中,对角线AC=BD.求证:平行四边形ABCD是矩形.分析:要证明□ABCD是矩形,只要证明有一个角是直角即可.证明:∴AB=CD,AB∥CD.∵AC=DB,BC=CB.∴ △ABC≌△DCB.∴∠ABC=∠DCB.∵四边形ABCD是平行四边形.∵∠ABC+∠DCB=180°.∴∠ABC=90°.∴四边形ABCD是矩形.对角线相等的平行四边形是矩形 。矩形的判定方法:几何语言:∵四边形ABCD是平行四边形
AC=BD∴四边形ABCD是矩形(对角线相等且互相平分的四边形是矩形。)(或OA=OC=OB=OD)12四边形有一个角是直角
有两个角是直角 的 四边形是矩形吗?
有三个角是直角
探究14情境一:李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?猜想:有三个角是直角的四边形是矩形 。你能证明上述结论吗?15定理:有三个角是直角的四边形是矩形.已知:如图,在四边形ABCD中, ∠A=∠B=∠C=90°.分析:利用同旁内角互补,两直线平行来证明四边形是平行四边形,可使问题得证.证明:∵ ∠A=∠B=∠C=90°.∴∠A+∠B=180°,∠B+∠C=180°.∴AD∥BC,AB∥CD.求证:四边形ABCD是矩形.∴四边形ABCD是平行四边形.∴四边形ABCD是矩形.矩形的判定方法:有三个角是直角的四边形是矩形 。 ∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形几何语言:17四边形有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形 。(对角线相等且互相平分的四边形是矩形。)有三个角是直角的四边形是矩形 。方法1:方法2:方法3:19矩形的三种判定方法定理:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.证明:∵ 四边形ABCD是矩形.∴∠A=90?,四边形ABCD是平行四边形.∴∠C=∠A=90?,
∠B=180?-∠A=90?,
∠D=180?-∠A=90?.求证:∠A=∠B=∠C=∠D=90?.∴四边形ABCD是矩形.定理:矩形的两条对角线相等.已知:如图,AC,BD是矩形ABCD的两条对角线.求证: AC=BD.证明:∵ 四边形ABCD是矩形.∴AB=DC,∠ABC=∠DCB=90°.分析:根据矩形的性质,可转化
为全等三角形(SAS)来证明.∵BC=CB.∴△ABC≌△DCB(SAS).∴AC=DB.定理:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.求证:△ABC是直角三角形.已知:CD是△ABC边AB上的中线,且分析:要证明△ABC是直角三角形,可以将点A,B,C构造平行四边形,然后证明其对角线相等,即可证明是矩形.下列各句判定矩形的说法是否正确?为什么?
(1)对角线相等的四边形是矩形;( )
(2)对角线互相平分且相等的四边形是矩形;( )
(3)有四个角是直角的四边形是矩形;( )
(4)对角线相等,且有一个角是直角的四边形是矩形;( )XX√ √ 谈一谈,今天你有何收获?1.判定一个四边形是矩形的方法是:本节课我们学习了什么内容,你能总结吗?小结:矩形的判定方法有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形 。(对角线相等且互相平分的四边形是矩形。)有三个角是直角的四边形是矩形 。方法1:方法2:方法3:25通过本课时的学习,需要我们掌握:
1、矩形的性质:
(1)矩形的四个角都是直角;
(2)矩形的对角线相等;
(3)推论:直角三角形斜边上的中线等于斜边的一半.
2、矩形的判定定理:
(1)定义:有一个角是直角的平行四边形是矩形;
(2)对角线相等的平行四边形是矩形;
(3)有三个角是直角的四边形是矩形.
3、直角三角形斜边上的中线等于斜边上的一半.1.如图所示,已知□ABCD,下列条件:①AC=BD,②AB=AD,③∠1=∠2,④AB⊥BC中,能说明□ABCD是矩形的有 (填写序号).解析:根据对角线相等的平行四边形是矩形;矩形的定义.
答案:① ④2.如图,在△ABC中,AB=AC=8,AD是底边上的高,E为AC的中点,则DE= .解析:根据直角三角形斜边的中线等于斜边的一半可得,DE等于AC的一半,所以DE=4.
答案:43.如图,在等边△ABC中,点D是BC边的中点,以AD为边作等边△ADE.(1)求∠CAE的度数;
(2)取AB边的中点F,连结CF、CE,试证明四边形AFCE是矩形.解析:(1)在等边△ABC中,∵点D是BC边的中点,∴∠DAC=30o,又∵等边△ADE,∴∠DAE=60o,∴∠CAE=30o.(2)在等边△ABC中,∵F是AB边的中点,D是BC边的中点,∴CF=AD,∠CFA=90o,又∵AD=AE,∴AE=CF,由(1)知∠CAE=30o,∴∠EAF=60o+30o=90o,∴∠CFA=∠EAF,∴CF∥AE,∵AE=CF,∴四边形AFCE是平行四边形,又∵∠CFA=90o,∴四边形AFCE是矩形.4.已知:如图,四边形ABCD是由两个全等的正三角形ABD和BCD组成的,M、N分别为BC、AD的中点.
求证:四边形BMDN是矩形.证明:在正三角形ABD和BCD中,M、N分别为BC、AD的中点.
∴BN⊥AD,DM⊥BC,∠DBC=60°,
∠BND=∠DMB=90°,∠NBD=30°.
∴∠NBM=90°.
∴四边形BMDN是矩形.5、已知:如图,AC,BD是矩形ABCD的两条对角线,AC,BD相交于点O,∠AOD=120°,AB=2.5cm.求矩形对角线的长.
解:∵四边形ABCD是矩形.
∴AC=BD,且
∴OA=OD.
∵∠AOD=120°.
∴∠ODA=∠OAD=
∵∠DAB=90°.
∴BD=2AB=2×2.5=5(cm).你认为本题还可以怎样解?
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
