力的合成典型例题讲解

课件11张PPT。力的合成 ——习题课
1、合力的大小与夹角θ的变化关系思考：若F1和F2的大小一定，夹角θ在0—1800内变化，合力F怎样变化？
（一）、合力与分力的关系F随夹角的变大而减小2、合力的范围
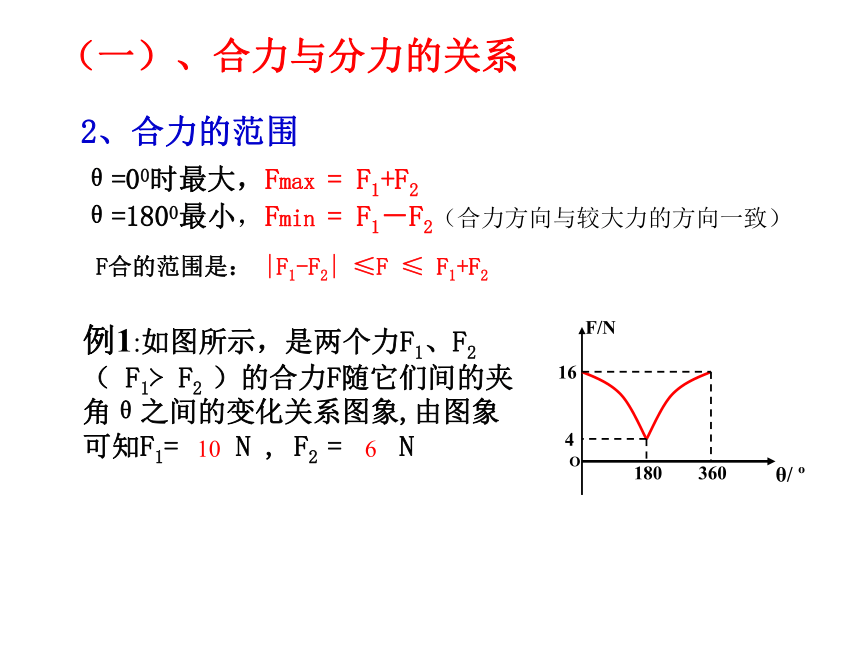
F合的范围是： |F1-F2| ≤F ≤ F1+F2（一）、合力与分力的关系例1:如图所示，是两个力F1、F2 （ F1?F2 ）的合力F随它们间的夹角θ之间的变化关系图象,由图象可知F1= N , F2 = N
θ=00时最大，Fmax = F1+F2
θ=1800最小，Fmin = F1－F2（合力方向与较大力的方向一致）1063、合力与分力的大小关系？ 合力可能比分力大
合力可能比分力小
合力可能等于分力
（一）、合力与分力的关系例2：有两个力，一个是５N，一个是７N，则它们的合力可能等于（ ）
A ２N B ５N C ７N D １２N ABCD4、一个分力不变，另外一个分力方向不变,大小增大，合力一定增大吗?二力共线:
同向时：分力增大，合力增大;
反向时：大力增大，合力增大;
小力增大，合力减小.
（一）、合力与分力的关系5、特殊情况下合力与分力的关系（一）、合力与分力的关系F合F合F= F tanα=例：求互成1200角的三个等大力F的合力？ 例：已知3个共点力的合力为零，则这3个力的大小可能是（ ）
A、3N、4N、8N B、6N、10N、2N
C、8N、7N、4N D、7N、9N、16N（二）、多个共点力的合成先求出任意两个力的合力，
再求这个合力与第三个力的合力例：求下列各组三个共点力的合力范围：
A 6N 9N 15N
B 4N 7N 8N
C 3N 5N 10N1、合成方法:0≤ F ≤ 300 ≤ F ≤ 192 ≤ F ≤ 18CD 例：三个共点力，F1=2N， F2=4N， F3=6N，互成1200 角， 求三个力的合力。F3=6NF2=4NF1=2N（二）、多个共点力的合成例：如图，六个共点力大小分别为１N、2N、3N、4N、5N、6N，最小力水平向右，依次顺时针方向排列，相邻间夹角为600,求这六个力的合力。
（二）、多个共点力的合成F合=F13+F2 =6N（三）、力的三角形定则F合例：有五个力作用于同一物体的O点，这五个力构成一个正六边形的两邻边和三条对角线，如图，设F3=10N，则这五个力的合力大小为多少？
（三）、力的三角形定则