第四章直线与角达标测试卷（含答案）

第四章达标测试卷
一、选择题(每题3分，共30分)
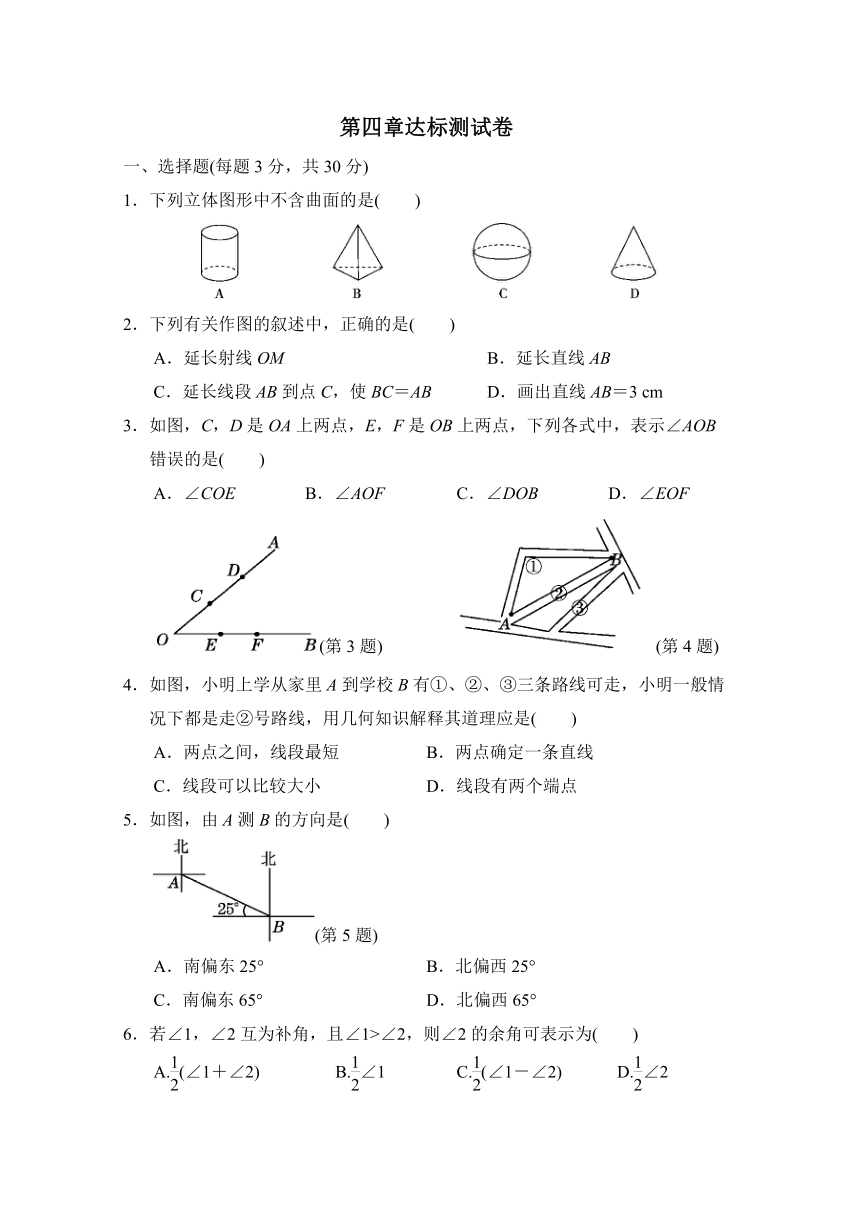
1．下列立体图形中不含曲面的是(　　)
2．下列有关作图的叙述中，正确的是(　　)
A．延长射线OM B．延长直线AB
C．延长线段AB到点C，使BC＝AB D．画出直线AB＝3 cm
3．如图，C，D是OA上两点，E，F是OB上两点，下列各式中，表示∠AOB错误的是(　　)
A．∠COE B．∠AOF C．∠DOB D．∠EOF
(第3题) (第4题)
4．如图，小明上学从家里A到学校B有①、②、③三条路线可走，小明一般情况下都是走②号路线，用几何知识解释其道理应是(　　)
A．两点之间，线段最短 B．两点确定一条直线
C．线段可以比较大小 D．线段有两个端点
5．如图，由A测B的方向是(　　)
(第5题)
A．南偏东25° B．北偏西25°
C．南偏东65° D．北偏西65°
6．若∠1，∠2互为补角，且∠1>∠2，则∠2的余角可表示为(　　)
A.(∠1＋∠2) B.∠1 C.(∠1－∠2) D.∠2
7．已知∠1＝76°36′，∠2＝76.3°，∠3＝76.6°，则(　　)
A．∠1＝∠2 B．∠2＝∠3 C．∠1＝∠3 D．以上都不对
8．已知点A，B，C共线，如果线段AB＝5 cm，BC＝4 cm，那么A，C两点间的距离是(　　)
A．1 cm B．9 cm C．1 cm或9 cm D．2 cm或10 cm
9．一副三角板按如图方式摆放，且∠1的度数比∠2的度数大54°，则∠1的度数为(　　)
A．72° B．70° C．54° D．18°
(第9题) (第10题)
10．如图所示，已知A，B是线段EF上两点，EA：AB：BF＝2：3：4，M，N分别为EA，BF的中点，且MN＝12cm，则EF长为(　　)
A．10 cm B．14 cm C．16 cm D．18 cm
二、填空题(每题3分，共12分)
11．农民兴修水利，开挖水渠，先在两端立柱拉线，然后沿线开挖，其中的道理是________．
12．一个角的余角是它的补角的，这个角是________度．
13．如图，点O在直线AB上，射线OC，OD在直线AB的同侧，∠AOD＝50°，∠BOC＝40°，OM，ON分别平分∠BOC和∠AOD，则∠MON的度数为________．
(第13题) (第14题)
14．如图，点A，B，C在同一直线上，H为AC的中点，M为AB的中点，N为BC的中点，则下列说法：①MN＝HC；②MH＝(AH－HB)；③MN＝(AC＋HB)；④HN＝(HC＋HB)，其中正确的是________．(填序号)
三、解答题(15～16题每题5分，17～20题每题6分，其余每题8分，共58分)
15．已知∠A＝143°26′29″，∠B＝96°41′24″，求下列算式的值：
(1)∠A＋2∠B； (2)∠A－∠B.
16. 已知∠α与∠β互余，且∠α比∠β小25°，求2∠α－∠β的值．
17. 如图，已知平面上点A，B，C，D.按下列要求画出图形：
(第17题)
(1)作直线AB，射线CB；
(2)取线段AB的中点E，连接DE并延长与射线CB交于点O；
(3)连接AD并延长至点F，使得AD＝DF.
18．如图，一副三角板的两个直角顶点重合在一起．
(1)比较∠EOM与∠FON的大小，并说明理由；
(2)若∠FOM＝60°，求∠EON的度数．
(第18题)
19．如图，已知线段AB的长度是a cm，线段BC的长度比线段AB长度的2倍多5 cm，线段AD的长度比线段BC长度的2倍少5 cm.
(1)写出用a表示的线段CD长的式子；
(2)当a＝15时，求线段CD的长．
(第19题)
20．在数学活动课中，学生们解答数学题“已知直线l上有两条线段AB，AC，
AB＝10 cm，AC＝6 cm，M，N分别是AB，AC的中点，求线段MN的长”时，出现了两种结果：MN＝8 cm和MN＝2 cm.请你判断两种结果是否正确，并说明原因．
21．如图，已知直线AB上有一点O，射线OD平分∠AOE，∠AOC：∠EOC＝1?4，且∠COD＝36°.
(第21题)
(1)求∠AOC的度数；
(2)求∠BOE的度数．
22．如图①，将一副三角尺的直角顶点重合在点O处．
(1)①∠AOD和∠BOC相等吗？说明理由．②∠AOC和∠BOD在数量上有何关系？说明理由．
(2)若将这副三角尺按如图②所示方式摆放，三角尺的直角顶点重合在点O处．
①∠AOD和∠BOC相等吗？说明理由．②∠AOC和∠BOD在数量上有何关系？说明理由．
(第22题)
23．情境：在数学活动课中，张老师拿出一根木条，标上中点，然后将木条折断成两根较短的木条，你能确定中点在哪一根木条上吗？
定义：如果一点在由两条有公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分，则这点叫做这条折线的“折中点”．如图，点D是折线A－C－B的“折中点”．
(第23题)
问题解决： (1)已知AC＝m，BC＝n.
当m＞n时，点D在线段________上；
当m＝n时，点D与________重合；
当m＜n时，点D在线段________上．
(2)若E为线段AC中点，EC＝4，CD＝3，求CB的长度．
答案
一、1.B　2.C　3.D　4.A　5.C　6.C　7．C　8.C　9.A
10．D　点拨：设EA＝2x，则AB＝3x，BF＝4x，AM＝EM＝x，BN＝FN＝2x，故MN＝AM＋AB＋BN＝x＋3x＋2x＝12，解得x＝2，
则EF＝2x＋3x＋4x＝9x＝18 cm.
二、11. 两点确定一条直线
12．60
13．135°　点拨：根据题意得∠AON＝∠AOD＝25°，∠BOM＝∠BOC＝20°，所以∠MON＝180°－∠AON－∠AOD＝180°－25°－20°＝135°.
14．①②④　点拨：由题意得AH＝CH＝AC，AM＝BM＝AB，BN＝CN＝BC，所以MN＝MB＋BN＝(AB＋BC)＝AC，所以MN＝HC，故结论①正确；(AH－HB)＝(AB－HB－HB)＝MB－HB＝MH，故结论②正确；因为MN＝AC，故结论③错误；(HC＋HB)＝(BC＋HB＋HB)＝BN＋HB＝HN，故结论④正确．综上所述，结论①②④正确．
三、15. 解：(1)∠A＋2∠B＝143°26′29″＋2×96°41′24″
＝143°26′29″＋192°82′48″
＝335°108′77″
＝336°49′17″.
(2)∠A－∠B＝143°26′29″－×96°41′24″
＝143°26′29″－48°20′42″
＝95°5′47″.
16．解：由题意得解得
2∠α－∠β＝2×32.5°－×57.5°＝45°50′.
17．解：如图所示．
(第17题)
18．解：(1)∠EOM＝∠FON.
理由是：因为∠EOM＋∠MOF＝∠FON＋∠MOF＝90°，
所以∠EOM＝∠FON.
(2)因为∠EOM＋∠MOF＝90°，∠FOM＝60°，
所以∠EOM＝30°.
又因为∠MON＝90°，
所以∠EON＝30°＋90°＝120°.
19．解：(1)BC＝2a＋5，
AD＝2BC－5＝2(2a＋5)－5＝4a＋5，
CD＝DA＋AB＋BC＝(4a＋5)＋a＋(2a＋5)＝7a＋10；
(2)当a＝15时，CD＝7×15＋10＝115(cm)．
20．解：两种结果都正确．
如图①所示，MN＝AB＋AC＝8 cm.
(第20题①)
如图②所示，MN＝AB－AC＝2 cm.
(第20题②)
21．解：(1)设∠AOC＝x，∠EOC＝4x，则∠AOE＝5x.
因为OD平分∠AOE，
所以∠AOD＝∠AOE＝x，
所以∠COD＝x－x＝x＝36°，
解得x＝24°，则∠AOC＝24°.
(2)因为∠AOE＝5x，
所以∠BOE＝180°－∠AOE＝180°－5×24°＝180°－120°＝60°.
22．解：(1)①∠AOD＝∠BOC.
理由如下：因为∠AOD＝90°＋∠BOD，
∠BOC＝90°＋∠BOD，
所以∠AOD＝∠BOC.
②∠AOC＋∠BOD＝180°.
理由如下：因为∠AOC＋90°＋∠BOD＋90°＝360°，
所以∠AOC＋∠BOD＝180°.
(2)①∠AOD＝∠BOC.
理由如下：因为∠AOD＝90°－∠BOD，
∠BOC＝90°－∠BOD，
所以∠AOD＝∠BOC.
②∠AOC＋∠BOD＝180°.理由如下：
因为∠AOC＝90°＋∠BOC，∠BOD＝90°－∠BOC，
所以∠AOC＋∠BOD＝180°.
23．解：(1)AC；点C；BC
(2)当点D在线段AC上时，
因为点E为线段AC中点，EC＝4，
所以AC＝2CE＝8.
所以AD＝AC－CD＝5，
则BC＋CD＝5.
所以BC＝5－3＝2.
当点D在线段BC上时，
因为点E为线段AC中点，EC＝4，
所以AC＝2CE＝8，
所以AC＋CD＝11，
则BD＝11，
所以BC＝11＋3＝14.