2.4.1线段的垂直平分线-试卷

2.4.1线段的垂直平分线
班级：___________姓名：___________得分：__________
（满分：100分，考试时间：40分钟）
一．选择题（共5小题，每题8分）
1．为了丰富学生的课余生活,某校举行联欢晚会,在联欢晚会上,有A,B,C三名同学站在一个三角形三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,凳子应放在△ABC的（ ）
A．三边中线的交点处 B．三条角平分线的交点处
C．三边高的交点处 D．三边垂直平分线的交点处
2．如图所示,在△ABC中,AB的垂直平分线交AC于点E,若AE=4?cm,则B,E两点之间的距离是（ ）
A．2?m B．3cm C．4cm D．5cm
/ / /
第2题图 第4题图 第5题图
3．下列说法错误的是（ ）
A．若E,D是线段AB的垂直平分线上的两点,则AD=BD,AE=BE
B．若AD=BD,AE=BE,D,E是不同的两点,则直线DE是线段AB的垂直平分线
C．若PA=PB,则点P在线段AB的垂直平分线上
D．若PA=PB,则过点P的直线是线段AB的垂直平分线
4．如图，在△ABE中，∠A=105°，AE的垂直平分线MN交BE于点C，且AB+BC=BE，则∠B的度数是（ ）
A．45° B．60° C．50° D．55°
5．如图，在四边形ABCD中，点D在线段AB、BC的垂直平分线上，若∠D=110°，则∠B度数为（ ）
A．110° B．115° C．120° D．125°
二．填空题（共4小题，每题5分）
6．线段是轴对称图形，它的一条对称轴是_____________，线段本身所在的直线也是它的一条对称轴．
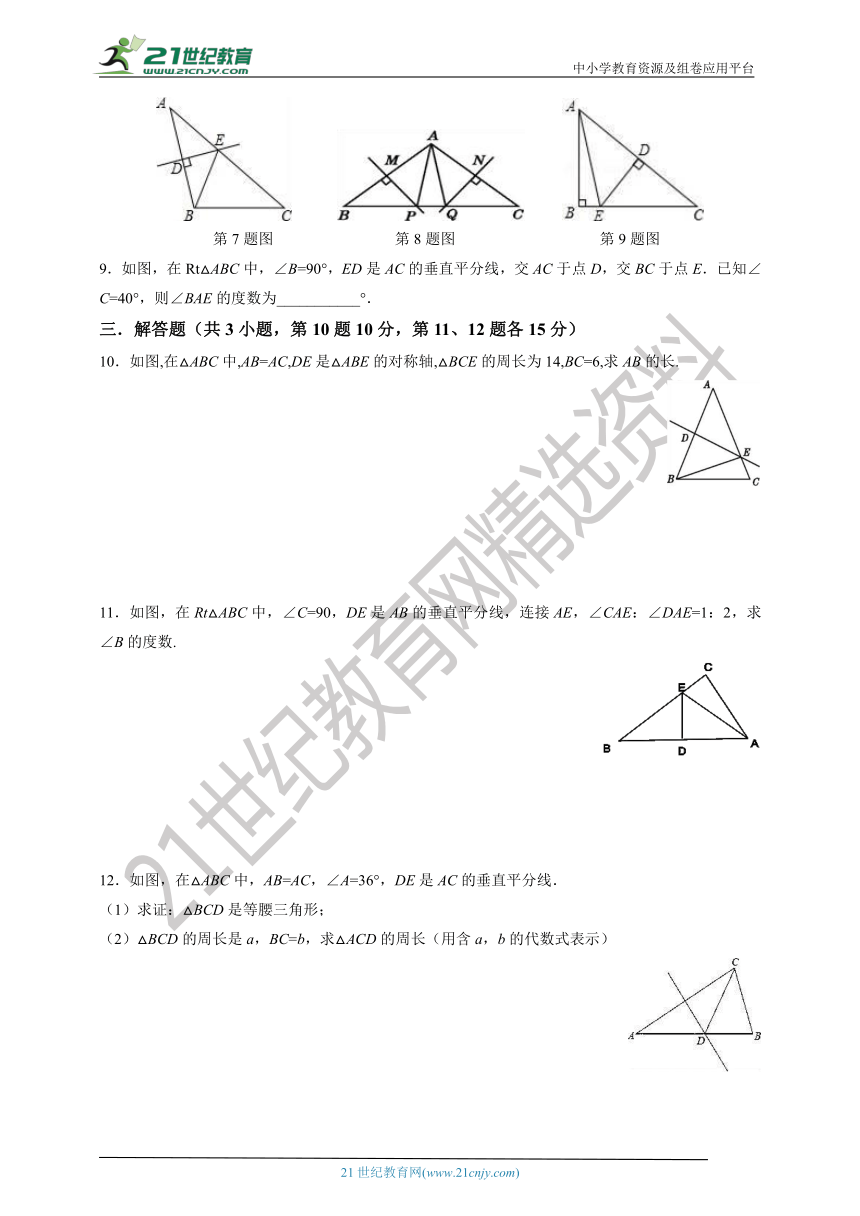
7．如图，在△ABC中，AC=10，BC=6，AB的垂直平分线交AB于点D，交AC于点E，则△BCE的周长是_____．
8．如图,MP,NQ分别垂直平分AB,AC,且BC=6 cm,则△APQ的周长为__________.
/ / /
第7题图 第8题图 第9题图
9．如图，在Rt△ABC中，∠B=90°，ED是AC的垂直平分线，交AC于点D，交BC于点E．已知∠C=40°，则∠BAE的度数为___________°．
三．解答题（共3小题，第10题10分，第11、12题各15分）
10．如图,在△ABC中,AB=AC,DE是△ABE的对称轴,△BCE的周长为14,BC=6,求AB的长.
/
11．如图，在Rt△ABC中，∠C=90，DE是AB的垂直平分线，连接AE，∠CAE：∠DAE=1：2，求∠B的度数.
/
12．如图，在△ABC中，AB=AC，∠A=36°，DE是AC的垂直平分线．
（1）求证：△BCD是等腰三角形；
（2）△BCD的周长是a，BC=b，求△ACD的周长（用含a，b的代数式表示）
/
试题解析
1．D
【解析】为使游戏公平，要使凳子到三个人的距离相等，于是利用线段垂直平分线上的点到线段两端的距离相等可知，要放在三边中垂线的交点上．
解：∵线段垂直平分线上的点到线段两个端点的距离相等
∴为使游戏公平，要使凳子到三个人的距离相等，这个点一定是三边的垂线的交点
故选：D．
2．C
【解析】首先连接BE，由DE是线段AB的垂直平分线，即可得BE=AE=4cm.
解：如图所示：连接BE，
/
∵DE是线段AB的垂直平分线，∴BE=AE，∵AE=4，
∴BE＝4.
故选C.
3．D
【解析】根据线段垂直平分线的性质定理及其逆定理，对各选项进行逐个验证，与之相符合的是正确的，反之，是错误的．
解：A选项：∵E是线段AB的垂直平分线上的点，
∴AE=BE．
同理AD=BD．
故A正确，与题意不符；B选项：若AD=BD，∴D在AB的垂直平分线上．
同理E在AB的垂直平分线上．
∴直线DE是线段AB的垂直平分线．
故B正确；C选项：若PA=PB，则点P在线段AB的垂直平分线上，
故C正确，与题意不符；D选项：若PA=PB，则点P在线段AB的垂直平分线上．但过点P的直线有无数条，不能确定过点P的直线是线段AB的垂直平分线．
故D错误，与题意相符．故选：D．
4．C
【解析】利用线段垂直平分线的性质知∠E=∠EAC AC=CE，等量代换得AB=CE=AC，利用三角形的外角性质得∠B=∠ACB=2∠E，从而根据三角形的内角和计算．
解：连接AC
∵CM⊥AE
∴∠E=∠EAC AC=CE（线段垂直平分线的性质）
∵AB+BC=BE（已知）
BC+CE=BE
∴AB=CE=AC（等量代换）
∴∠B=∠ACB=2∠E（外角性质）
∵∠B+∠E+105°=180°（三角形内角和）
∴∠B+/∠B+105°=180°
解得∠B=50°．
故选C．
/
5．D
【解析】连接BD，根据线段的垂直平分线性质可得BD=AD，DC=BD，由等腰三角形的性质可得∠A=∠ABD，∠C=∠CBD，即可得∠ABC=∠ABD+∠CBD=∠A+∠C，根据四边形的内角和为360°即可求出答案．
解：接BD，
/
∵点D在线段AB、BC的垂直平分线上，
∴BD=AD，DC=BD，
∴∠A=∠ABD，∠C=∠CBD，
∴∠ABC=∠ABD+∠CBD=∠A+∠C，
∴∠ABC=（360°﹣∠D）÷2=125°．
故选D．
6．线段的垂直平分线
【解析】线段的对称轴为线段的中垂线．
解：线段是轴对称图形，它的一条对称轴是线段的垂直平分线，线段本身所在的直线也是它的一条对称轴．
7．16
【解析】由线段垂直平分线上的点到线段两端点的距离相等可求出AE=BE，进而求出△BCE的周长.
解：∵DE是AB的垂直平分线，
∴AE=BE，
∵AC=10cm，BC=6cm，
∴△BCE的周长=BC+BE+CE=BC+AE+CE=BC+AC=10+6=16cm．
故答案为：16
8．6 cm
【解析】由MP、NQ分别垂直平分AB、AC，根据线段垂直平分线的性质，可得BP=AP，CQ=AQ，继而求得△APQ的周长等于BC．
解：∵MP、NQ分别垂直平分AB、AC，
∴BP=AP，CQ=AQ，
∵BC=6cm，
∴△APQ的周长为：AP+PQ+AQ=BP+PQ+CQ=BC=6cm.
故答案为： 6 cm.
9．10
【解析】∵ED是AC的垂直平分线，
∴AE=CE，
∴∠EAC=∠C=40°，
∵在Rt△ABC中,∠B=90°，
∴∠BAC=90°?∠C=50°，
∴∠BAE=∠BAC?∠EAC=10°.
故答案为：10.
10．8
【解析】由DE是△ABE的对称轴，根据轴对称的性质可得AE=BE，再由C△BCE=BC+CE+BE=14，可得BC+AC=14，从而求得AB的长.
解：因为DE是△ABE的对称轴,
所以AE=BE.
所以C△BCE=BC+CE+BE=BC+CE+AE=BC+AC=14.
因为BC=6,所以AC=8.
所以AB=AC=8.
/
12．（1）证明见解析；（2）a﹣b+b+b=a+b．
【解析】（1）先由AB=AC，∠A=36°，可求∠B=∠ACB==72°，然后由DE是AC的垂直平分线，可得AD=DC，进而可得∠ACD=∠A=36°，然后根据外角的性质可求：∠CDB=∠ACD+∠A=72°，根据等角对等边可得：CD=CB，进而可证△BCD是等腰三角形；
（2）由（1）知：AD=CD=CB=b，由△BCD的周长是a，可得AB=a﹣b，由AB=AC，可得AC=a﹣b，进而得到△ACD的周长=AC+AD+CD=a﹣b+b+b=a+b．
（1）证明：∵AB=AC，∠A=36°，
∴∠B=∠ACB=/=72°，
∵DE是AC的垂直平分线，
∴AD=DC，
∴∠ACD=∠A=36°，
∵∠CDB是△ADC的外角，
∴∠CDB=∠ACD+∠A=72°，
∴∠B=∠CDB，
∴CB=CD，
∴△BCD是等腰三角形；
（2）解：∵AD=CD=CB=b，△BCD的周长是a，
∴AB=a﹣b，
∵AB=AC，
∴AC=a﹣b，
∴△ACD的周长=AC+AD+CD=a﹣b+b+b=a+b．
/